代码随想录 -- 数组
文章目录
- 二分查找
- 题目描述
- 题解
- 移除元素
- 题目描述
- 题解:暴力解法
- 题解:双指针法
- 有序数组的平方
- 题目描述
- 题解:暴力解法
- 题解:双指针法
- 长度最小的子数组
- 题目描述
- 题解:暴力解法
- 题解:滑动窗口(双指针)
- 螺旋矩阵II
- 题目描述
- 题解
二分查找
力扣题目链接
题目描述
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
题解
class Solution {
public:int search(vector<int>& nums, int target) {int low=0,high = nums.size()-1,mid;while (low<=high){mid=(low+high)>>1;if (nums.at(mid) == target)return mid;else if(nums.at(mid)>target) high = mid-1;else low = mid+1;}return -1;}
};
移除元素
力扣题目链接
题目描述
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
题解:暴力解法
class Solution {
public:int removeElement(vector<int>& nums, int val) {size_t len = nums.size();for (int i = 0; i < len; ++i) {if(nums[i] == val){for (int j = i; j < len-1; ++j) {nums[j] = nums[j+1];}--i;// 因为下标i以后的数值都向前移动了一位,所以i也向前移动一位--len;}}return len;}
};
题解:双指针法
class Solution {
public:int removeElement(vector<int>& nums, int val) {int slowIndex{0},fastIndex{0};while (fastIndex<nums.size()){if(val!=nums[fastIndex])nums[slowIndex++] = nums[fastIndex];++fastIndex;}return slowIndex;}
};
有序数组的平方
力扣题目链接
题目描述
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100],排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
题解:暴力解法
先平方后排序
class Solution {
public:vector<int> sortedSquares(vector<int>& nums) {for (auto &item: nums)item*=item;sort(nums.begin(),nums.end());return nums;}
};
题解:双指针法
分析:
数组是有序的,那么数组里面的元素平方之后的最大值要么是开头的要么是结尾的,依次移动
class Solution {
public:vector<int> sortedSquares(vector<int>& nums) {size_t n = nums.size()-1;size_t slowIndex{0},fastIndex{n};vector<int>result(n+1,0);while (slowIndex<fastIndex) {int s1 = nums[slowIndex] * nums[slowIndex],s2 = nums[fastIndex] * nums[fastIndex];if (s1 > s2){result[n--] = s1;++slowIndex;}else {result[n--] = s2;--fastIndex;}}result[0]=nums[slowIndex]*nums[slowIndex];return result;}
};
代码简写的版本:
class Solution {
public:vector<int> sortedSquares(vector<int>& A) {int k = A.size() - 1;vector<int> result(A.size(), 0);for (int i = 0, j = A.size() - 1; i <= j;) { // 注意这里要i <= j,因为最后要处理两个元素if (A[i] * A[i] < A[j] * A[j]) {result[k--] = A[j] * A[j];j--;}else {result[k--] = A[i] * A[i];i++;}}return result;}
};
长度最小的子数组
力扣题目链接
题目描述
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
提示:
1 <= target <= 10^9
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5
题解:暴力解法
已经超时
class Solution {
public:int minSubArrayLen(int target, vector<int> &nums) {size_t len = nums.size();if (len == 0)return 0;int min_o = INT_MAX;for (int i = 0; i < len; ++i) {int sum{0};for (int j = i; j < len; ++j) {sum += nums[j];if (sum >= target){min_o = (min_o < (j - i + 1)) ? min_o : (j - i + 1);break;}}}return min_o == INT_MAX ? 0 : min_o;}
};
题解:滑动窗口(双指针)
class Solution {
public:int minSubArrayLen(int target, vector<int> &nums) {size_t len = nums.size();// beg:起始位置 sum:总和 result:最终的结果int beg{0}, sum{0}, result{INT_MAX};// i是一个中止位置for (int i = 0; i < len; ++i) {sum += nums[i];// 持续更新起始位置,当满足条件的时候起始位置前移while (sum >= target) {// 选择最小窗口result = (result < (i - beg + 1)) ? result : (i - beg + 1);sum -= nums[beg++];}}return result == INT_MAX ? 0 : result;}
};
螺旋矩阵II
力扣题目链接
题目描述
给定一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
题解
class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>>v(n,vector<int>(n,0));//offset偏移量 count总数int offset{1},start_x{0},start_y{0},i{0},j{0},count{1};// 循环n/2次 奇数特殊处理一下 偶数直接结束int loop = n/2;//循环的次数while(loop--){for (j = start_y; j < n - offset; ++j)v[start_x][j] = count++;for (i = start_x ; i < n - offset; ++i)v[i][j] = count++;for (; j > start_y; --j)v[i][j] = count++;for (; i > start_x; --i)v[i][j] = count++;++start_x;++start_y;++offset;}if (n%2!=0)v[n/2][n/2] = count;return v;}
};
相关文章:

代码随想录 -- 数组
文章目录 二分查找题目描述题解 移除元素题目描述题解:暴力解法题解:双指针法 有序数组的平方题目描述题解:暴力解法题解:双指针法 长度最小的子数组题目描述题解:暴力解法题解:滑动窗口(双指针…...

【国产MCU】-CH32V307-基本定时器(BCTM)
基本定时器(BCTM) 文章目录 基本定时器(BCTM)1、基本定时器(BCTM)介绍2、基本定时器驱动API介绍3、基本定时器使用实例CH32V307的基本定时器模块包含一个16 位可自动重装的定时器(TIM6和TIM7),用于计数和在更新新事件产生中断或DMA 请求。 本文将详细介绍如何使用CH32…...

Node.js开发-fs模块
这里写目录标题 fs模块1) 文件写入2) 文件写入3) 文件移动与重命名4) 文件删除5) 文件夹操作6) 查看资源状态7) 相对路径问题8) __dirname fs模块 fs模块可以实现与硬盘的交互,例如文件的创建、删除、重命名、移动等,还有文件内容的写入、读取ÿ…...

探索Nginx:强大的开源Web服务器与反向代理
一、引言 随着互联网的飞速发展,Web服务器在现代技术架构中扮演着至关重要的角色。Nginx(发音为“engine x”)是一个高性能的HTTP和反向代理服务器,也是一个IMAP/POP3/SMTP代理服务器。Nginx因其卓越的性能、稳定性和灵活性&…...
相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...
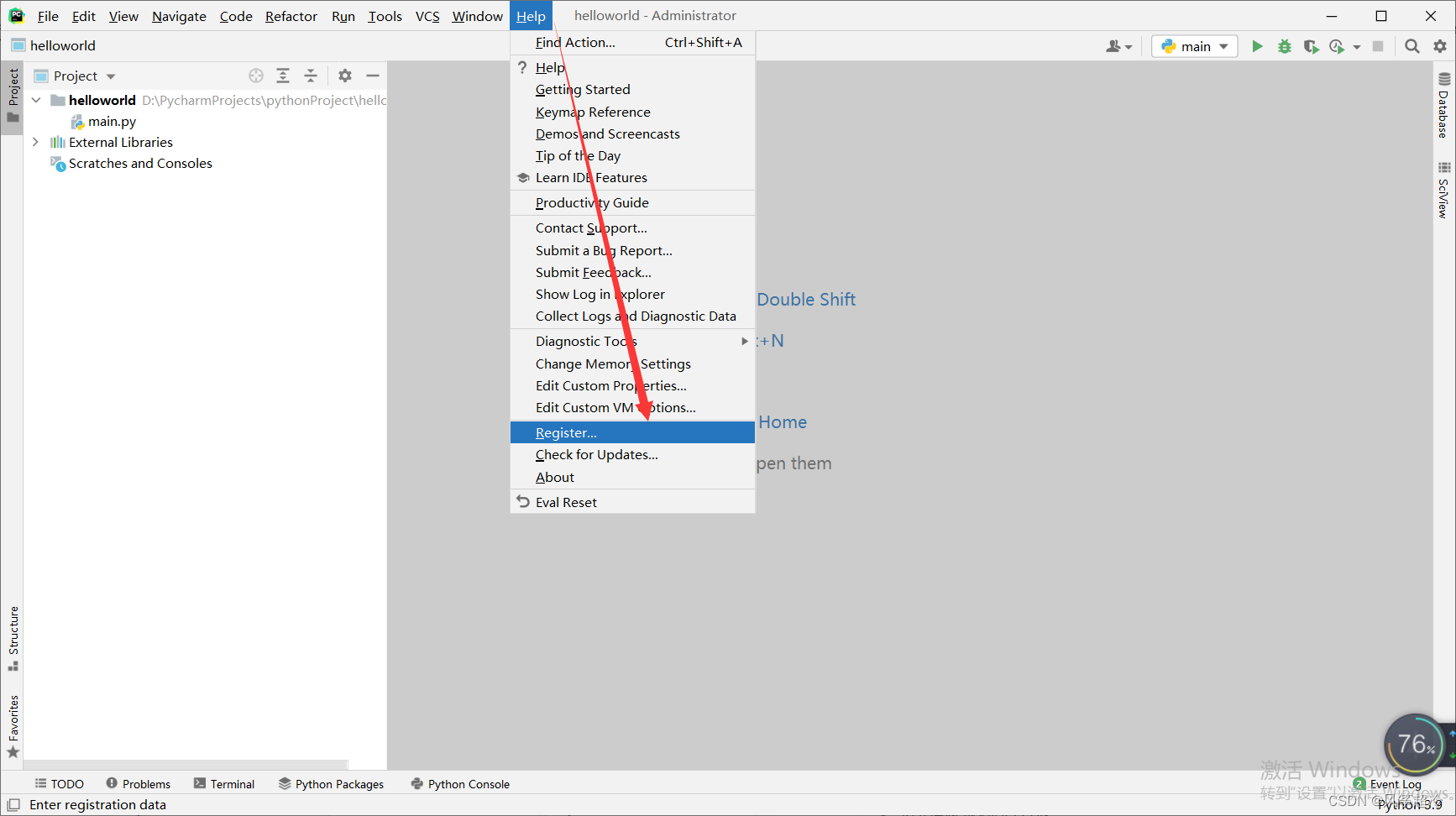
【从Python基础到深度学习】1. Python PyCharm安装及激活
前言: 为了帮助大家快速入门机器学习-深度学习,从今天起我将用100天的时间将大学本科期间的所学所想分享给大家,和大家共同进步。【从Python基础到深度学习】系列博客中我将从python基础开始通过知识和代码实践结合的方式进行知识的分享和记…...
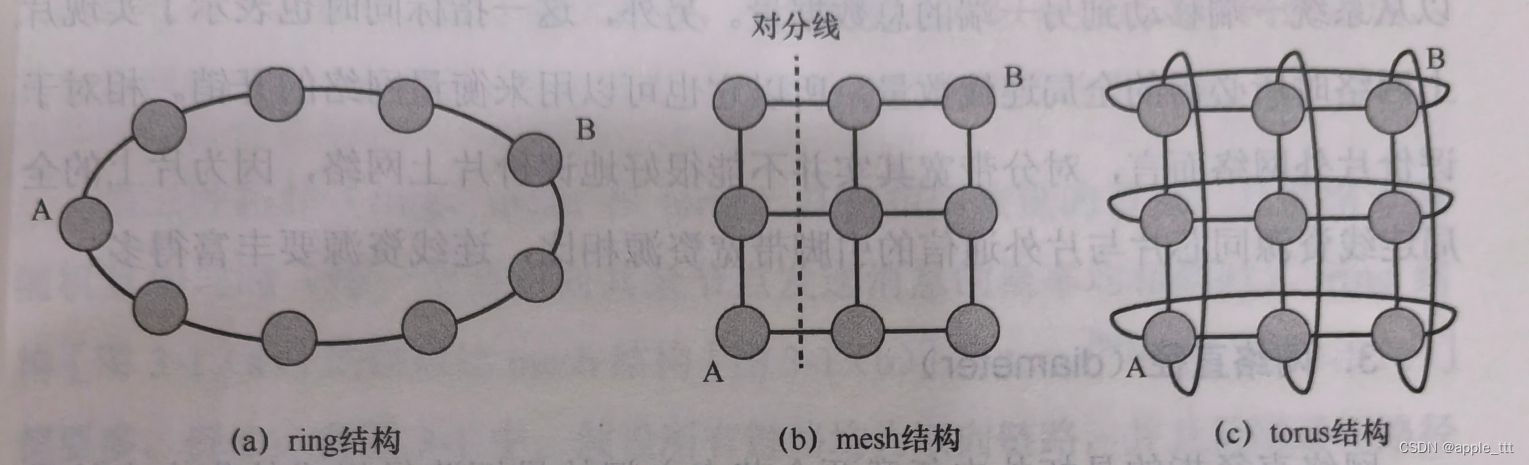
片上网络NoC(3)——拓扑指标
目录 一、概述 二、指标 2.1 与网络流量无关的指标 2.1.1 度(degree) 2.1.2 对分带宽(bisection bandwidth) 2.1.3 网络直径(diameter) 2.2 与网络流量相关的指标 2.2.1 跳数(hop coun…...

二叉树 ---- 所有结点数
普通二叉树的结点数: 递归法: 对二叉树进行前序or后序遍历: typedef struct Tree {int data;Tree* leftChild;Tree* rightChild; }tree,*linklist; //计算普通二叉树的结点数 int nodenums(linklist node) {if(node nullptr) return 0; …...
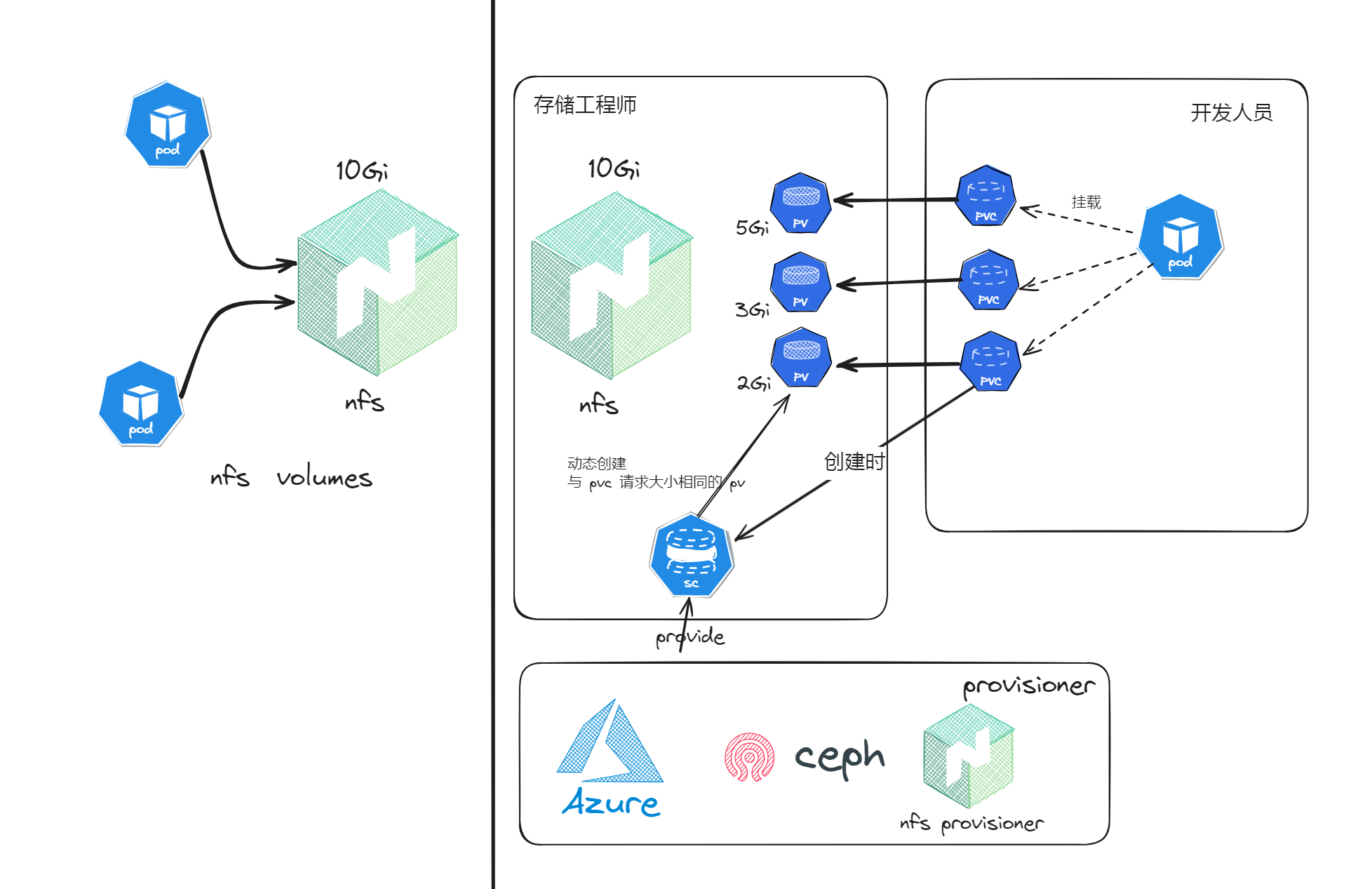
步步深入 k8s 使用 pv pvc sc 在 nfs 基础上共享存储
博客原文 文章目录 前言集群环境nfs 环境搭建pod 挂载 nfs架构图 pvc 方式挂载 nfs架构图 storageclass 方式动态申请 pv架构图 参考 前言 持久化卷(Persistent Volume, PV)允许用户将外部存储映射到集群,而持久化卷申请(Persist…...
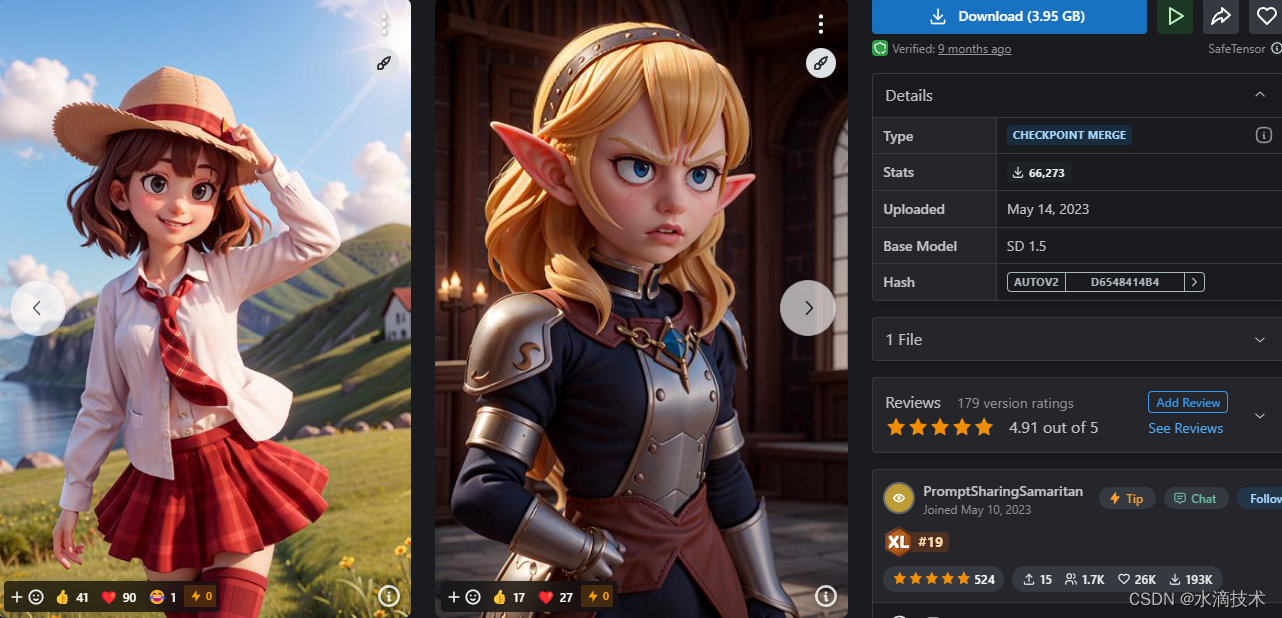
Stable Diffusion 模型下载:Disney Pixar Cartoon Type A(迪士尼皮克斯动画片A类)
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八案例九案例十...
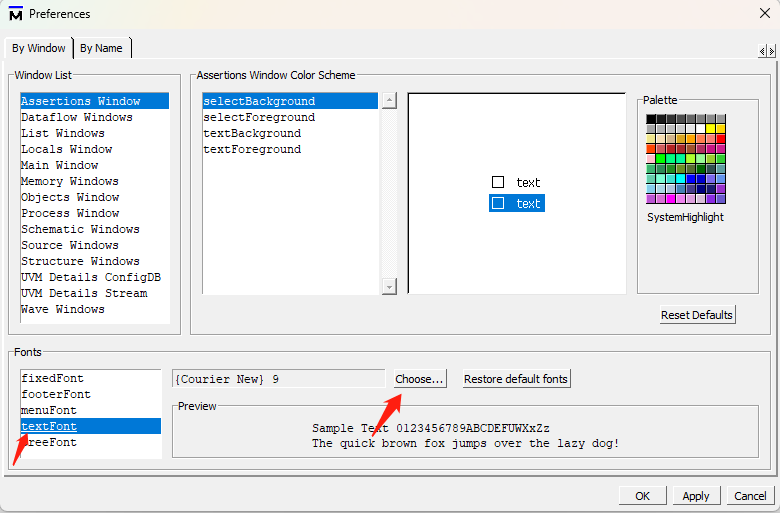
Modelsim10.4安装
简介(了解,可跳过) modelsim是Mentor公司开发的优秀的HDL语言仿真软件。 它能提供友好的仿真环境,采用单内核支持VHDL和Verilog混合仿真的仿真器。它采用直接优化的编译技术、Tcl/Tk技术和单一内核仿真技术,编译仿真速…...
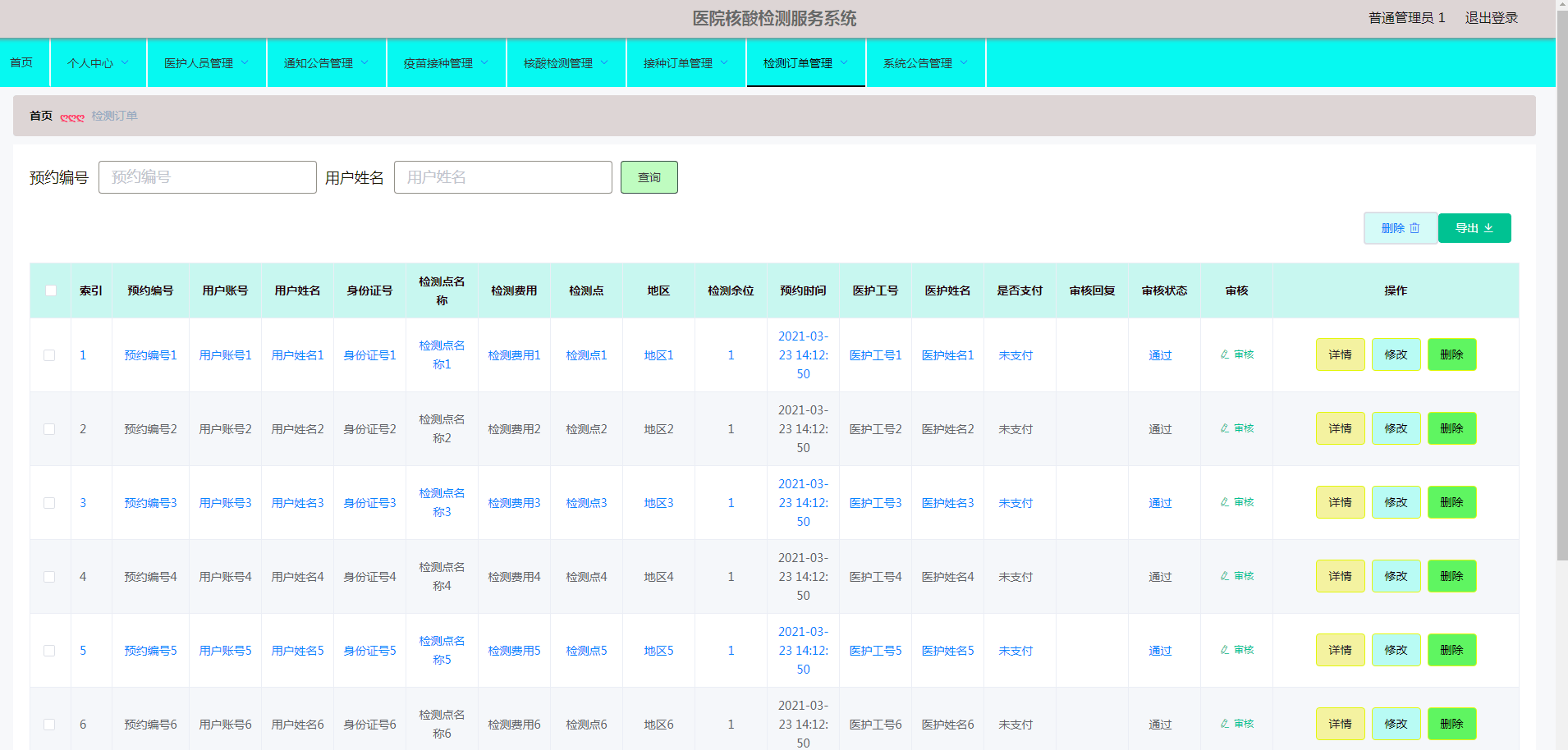
Java基于微信小程序的医院核酸检测服务系统,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
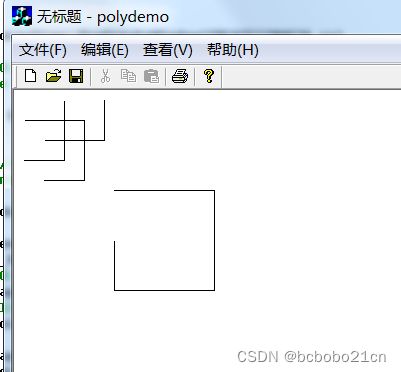
VC++ 绘制折线学习
win32 有三个绘制折线的函数; Polyline,根据给定点数组绘制折线; PolylineTo,除了绘制也更新当前位置; PolyPolyline,绘制多条折线,第一个参数是点数组,第二个参数是一个数组、指…...

速盾:dns解析和cdn加速的区别与联系
DNS解析和CDN加速是两种不同的网络技术,但在网站访问过程中起到了相互协作的作用。 首先,DNS解析(Domain Name System)是将域名转换为IP地址的过程。当用户输入一个网址时,计算机会先向本地DNS服务器发送一个查询请求…...
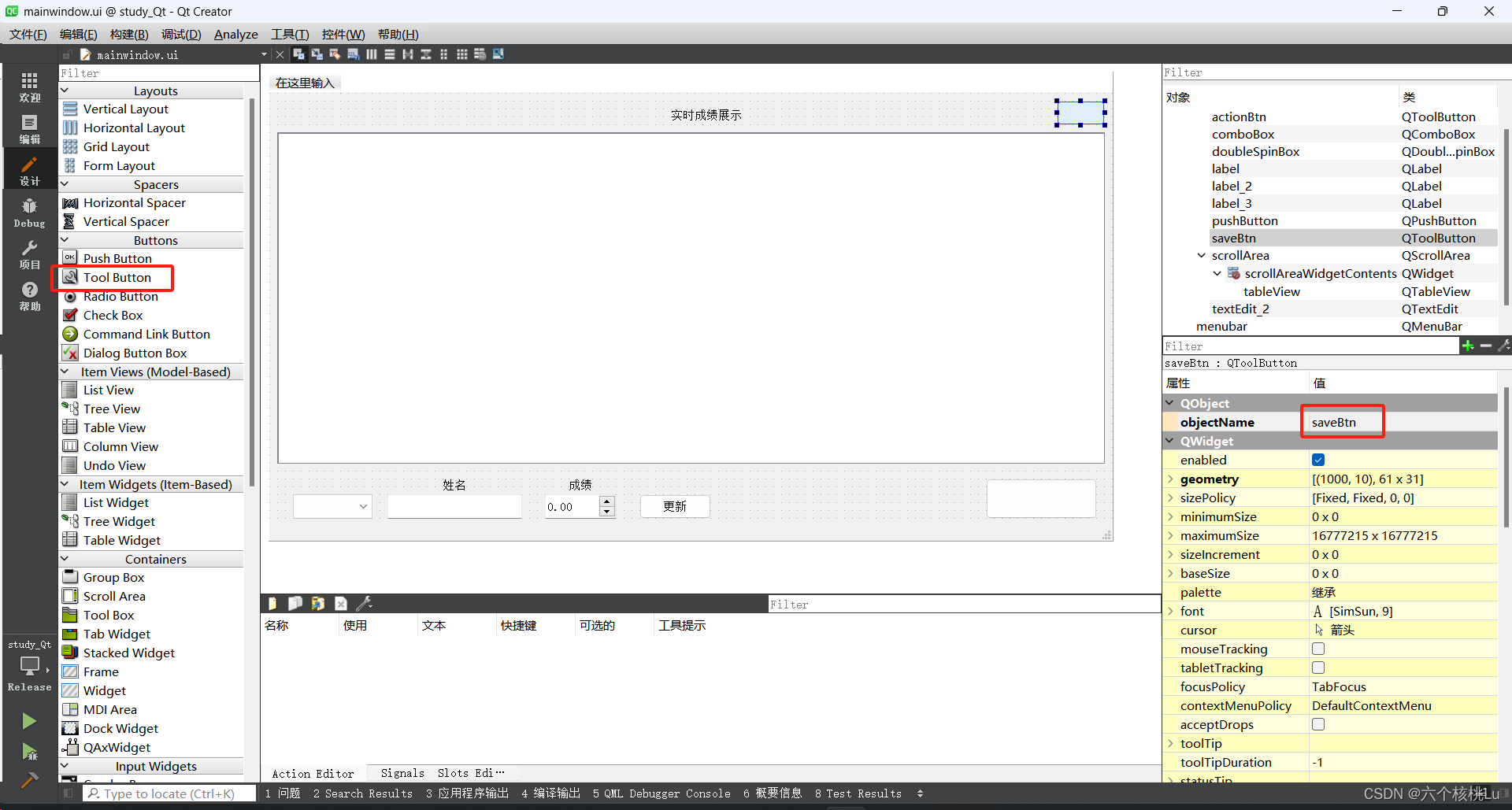
C++ Qt框架开发 | 基于Qt框架开发实时成绩显示排序系统(3) 保存表格数据
对上两篇篇的工作C Qt框架开发| 基于Qt框架开发实时成绩显示排序系统(1)-CSDN博客和C Qt框架开发 | 基于Qt框架开发实时成绩显示排序系统(2)折线图显示-CSDN博客继续优化,增加一个保存按钮,用于保存成绩数据…...

ChatGPT 4:新特性与优势
ChatGPT 4:新特性与优势 一、引言 ChatGPT 4是一款备受瞩目的人工智能模型,它以其强大的语言生成能力和智能回答能力,为用户提供了更高效、更便捷的对话体验。为了能够充分享受ChatGPT 4的各项功能,本文将向您详细介绍其新特性&…...

【教程】MySQL数据库学习笔记(二)——数据类型(持续更新)
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【MySQL数据库学习】系列文章 第一章 《认识与环境搭建》 第二章 《数据类型》 文章目录 【MySQL数据库学习】系列文章一、整…...

Servo的并发模型介绍
Servo是一个由Mozilla Research开发的实验性浏览器引擎,旨在为未来的网页和应用程序提供高性能的渲染。Servo的并发模型是其核心特点之一,它利用现代多核处理器的优势,通过异步编程和并行处理来提高渲染效率和响应性。以下是对Servo并发模型的…...
Vue3大事件项目(ing)
文章目录 核心内容1.大事件项目介绍2.大事件项目创建3.Eslint配置代码风格4.配置代码检查工作流问题: pnpm lint是全量检查,耗时问题,历史问题 5.目录调整6.vue-router4 路由代码解析7.引入 Element Plus 组件库8.Pinia 构建仓库 和 持久化9.Pinia 仓库统一管理 核心内容 Vue3…...
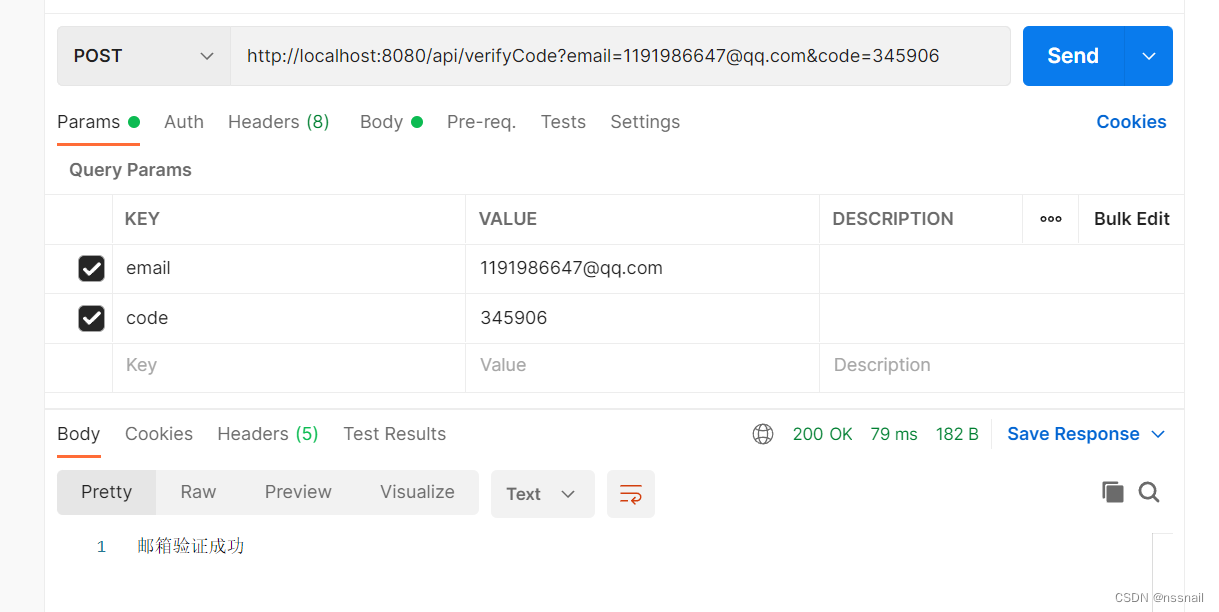
基于spring boot实现邮箱发送和邮箱验证
目录 一、邮箱发送实现1. 开通邮箱服务2. 添加邮箱依赖3.添加配置4.添加邮箱通用类5. 测试类 二、邮箱验证实现1.添加依赖2. 添加配置3.添加controller4. 测试 项目地址: https://gitee.com/nssnail/springboot-email 一、邮箱发送实现 1. 开通邮箱服务 使用qq邮箱、163邮箱都…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
