λ-矩阵的多项式展开
原文链接
定义. 对于 m × n m \times n m×n 的 λ \lambda λ-矩阵 A ( λ ) = [ a 11 ( λ ) . . . a 1 n ( λ ) ⋮ ⋮ a m 1 ( λ ) . . . a m n ( λ ) ] \mathbf{A}(\lambda)=\begin{bmatrix} a_{11}(\lambda) & ... & a_{1n}(\lambda)\\ \vdots & & \vdots \\ a_{m1}(\lambda) & ... & a_{mn}(\lambda) \end{bmatrix} A(λ)= a11(λ)⋮am1(λ)......a1n(λ)⋮amn(λ)
称 L = max 1 ≤ i ≤ m 1 ≤ j ≤ n deg { a i j ( λ ) } L=\max\limits_{1\leq i\leq m\atop{1\leq j \leq n}}\deg \{a_{ij}(\lambda)\} L=1≤j≤n1≤i≤mmaxdeg{aij(λ)} 为 A ( λ ) \mathbf{A}(\lambda) A(λ) 的次数, 显然每个元素的次数不超过 L L L.
定理. 对于 m × n m \times n m×n 的 λ \lambda λ-矩阵 A ( λ ) \mathbf{A}(\lambda) A(λ), 次数为 L L L, 存在唯一的一组常数 m × n m \times n m×n 矩阵 A 0 \mathbf{A}_0 A0, . . . ... ..., A L \mathbf{A}_{L} AL, 使得: A ( λ ) = A 0 + A 1 λ + . . . + A L λ L \mathbf{A}(\lambda)=\mathbf{A}_{0}+\mathbf{A}_{1}\lambda+...+\mathbf{A}_{L}\lambda^{L} A(λ)=A0+A1λ+...+ALλL (称之为 A ( λ ) \mathbf{A}(\lambda) A(λ) 的多项式展开式).
存在性: 设
A ( λ ) = [ a 11 ( λ ) . . . a 1 n ( λ ) ⋮ ⋮ a m 1 ( λ ) . . . a m n ( λ ) ] \mathbf{A}(\lambda)=\begin{bmatrix} a_{11}(\lambda) & ... & a_{1n}(\lambda)\\ \vdots & & \vdots \\ a_{m1}(\lambda) & ... & a_{mn}(\lambda) \end{bmatrix} A(λ)= a11(λ)⋮am1(λ)......a1n(λ)⋮amn(λ)
其中 a i j ( λ ) = a i j 0 + a i j 1 λ + . . . + a i j L λ L , 1 ≤ i ≤ m , 1 ≤ j ≤ n a_{ij}(\lambda)=a_{ij}^{0}+a_{ij}^{1}\lambda + ... + a_{ij}^{L}\lambda^{L}, \ 1 \leq i \leq m, \ 1 \leq j \leq n aij(λ)=aij0+aij1λ+...+aijLλL, 1≤i≤m, 1≤j≤n, 令 A r = [ a 11 r . . . a 1 n r ⋮ ⋮ a m 1 r . . . a m n r ] , 0 ≤ r ≤ L \mathbf{A}_{r}=\begin{bmatrix} a_{11}^{r} & ... & a_{1n}^{r}\\ \vdots & & \vdots \\ a_{m1}^{r} & ... & a_{mn}^{r} \end{bmatrix},\ 0\leq r\leq L Ar= a11r⋮am1r......a1nr⋮amnr , 0≤r≤L
则可以将 A ( λ ) \mathbf{A}(\lambda) A(λ) 表示为 A ( λ ) = A 0 + A 1 λ + . . . + A L λ L \mathbf{A}(\lambda)=\mathbf{A}_{0}+\mathbf{A}_{1}\lambda+...+\mathbf{A}_{L}\lambda^{L} A(λ)=A0+A1λ+...+ALλL.
唯一性: 若不唯一, 则设存在另外一组 m × n m \times n m×n 矩阵 A 0 ′ \mathbf{A}'_0 A0′, …, A L ′ \mathbf{A}'_{L} AL′, 使得: A ( λ ) = A 0 ′ + A 1 ′ λ + . . . + A L ′ λ L \mathbf{A}(\lambda)=\mathbf{A}'_{0}+\mathbf{A}'_{1}\lambda+...+\mathbf{A}'_{L}\lambda^{L} A(λ)=A0′+A1′λ+...+AL′λL.
A ( λ ) = A 0 + A 1 λ + . . . + A L λ L = A 0 ′ + A 1 ′ λ + . . . + A L ′ λ L \mathbf{A}(\lambda)=\mathbf{A}_{0}+\mathbf{A}_{1}\lambda+...+\mathbf{A}_{L}\lambda^{L}=\mathbf{A}'_{0}+\mathbf{A}'_{1}\lambda+...+\mathbf{A}'_{L}\lambda^{L} A(λ)=A0+A1λ+...+ALλL=A0′+A1′λ+...+AL′λL
( A 0 − A 0 ′ ) + ( A 1 − A 1 ′ ) λ + . . . + ( A L − A L ′ ) λ L = 0 (\mathbf{A}_{0}-\mathbf{A}'_{0})+(\mathbf{A}_{1}-\mathbf{A}'_{1})\lambda+...+(\mathbf{A}_{L}-\mathbf{A}'_{L})\lambda^L=\mathbf{0} (A0−A0′)+(A1−A1′)λ+...+(AL−AL′)λL=0
比较系数可知 A 0 = A 0 ′ \mathbf{A}_{0}=\mathbf{A}'_{0} A0=A0′,…, A L = A L ′ \mathbf{A}_{L}=\mathbf{A}'_{L} AL=AL′. 矛盾.
存在性的过程也提供了展开式的求法.
定理. A ( λ ) \mathbf{A}(\lambda) A(λ) 和 B ( λ ) \mathbf{B}(\lambda) B(λ) 是 n n n 阶 λ \lambda λ-矩阵, 记 deg A ( λ ) = L \deg \mathbf{A}(\lambda)=L degA(λ)=L, deg B ( λ ) = M \deg \mathbf{B}(\lambda)=M degB(λ)=M, 有: L , M > 0 L, M \gt 0 L,M>0, 且 B ( λ ) \mathbf{B}(\lambda) B(λ) 的多项式展开式中 λ M \lambda^{M} λM 项的系数矩阵可逆, 则存在 n n n 阶 λ \lambda λ-矩阵 U ( λ ) \mathbf{U}(\lambda) U(λ), V ( λ ) \mathbf{V}(\lambda) V(λ), deg V ( λ ) < M \deg\mathbf{V}(\lambda)<M degV(λ)<M, 使得 A ( λ ) = U ( λ ) B ( λ ) + V ( λ ) \mathbf{A}(\lambda)=\mathbf{U}(\lambda)\mathbf{B}(\lambda)+\mathbf{V}(\lambda) A(λ)=U(λ)B(λ)+V(λ).
证明: 当 L < M L<M L<M 时, 令 U ( λ ) = 0 \mathbf{U}(\lambda)=\mathbf{0} U(λ)=0, V ( λ ) = A ( λ ) \mathbf{V}(\lambda)=\mathbf{A}(\lambda) V(λ)=A(λ), 显然 U ( λ ) \mathbf{U}(\lambda) U(λ) 和 V ( λ ) \mathbf{V}(\lambda) V(λ) 即为所求. 接下来用数学归纳法证明当 L ≥ M L\geq M L≥M 时结论成立:
当 L = M = 1 L=M=1 L=M=1 时, 设 A ( λ ) = A 0 + A 1 λ \mathbf{A}(\lambda)=\mathbf{A}_0+\mathbf{A}_1 \lambda A(λ)=A0+A1λ, B ( λ ) = B 0 + B 1 λ \mathbf{B}(\lambda)=\mathbf{B}_0+\mathbf{B}_1 \lambda B(λ)=B0+B1λ, 令 U ( λ ) = A 1 B 1 − 1 \mathbf{U}(\lambda)=\mathbf{A}_1\mathbf{B}_{1}^{-1} U(λ)=A1B1−1, V ( λ ) = A 0 − A 1 B 1 − 1 \mathbf{V}(\lambda)=\mathbf{A}_0-\mathbf A_1\mathbf B_{1}^{-1} V(λ)=A0−A1B1−1 即为所求.
若结论对于 L = k L=k L=k 成立, 当 L = k + 1 L=k+1 L=k+1 时: 设 A ( λ ) = A 0 + A 1 λ + . . . + A L λ L \mathbf{A}(\lambda)=\mathbf{A}_{0}+\mathbf{A}_{1}\lambda+...+\mathbf{A}_{L}\lambda^{L} A(λ)=A0+A1λ+...+ALλL, B ( λ ) = B 0 + B 1 λ + . . . + B M λ M \mathbf{B}(\lambda)=\mathbf{B}_{0}+\mathbf{B}_{1}\lambda+...+\mathbf{B}_{M}\lambda^{M} B(λ)=B0+B1λ+...+BMλM, 令 A ′ ( λ ) = A ( λ ) − A L B M − 1 λ L − M B ( λ ) \mathbf {A}'(\lambda) = \mathbf{A}(\lambda)-\mathbf{A}_{L}\mathbf{B}^{-1}_{M}\lambda^{L-M}\mathbf{B}(\lambda) A′(λ)=A(λ)−ALBM−1λL−MB(λ), 易验证 A ′ ( λ ) \mathbf{A}'(\lambda) A′(λ) 次数小于 L L L, 根据归纳假设, 存在 n n n 阶 λ \lambda λ-矩阵 U ′ ( λ ) \mathbf{U}'(\lambda) U′(λ), V ′ ( λ ) \mathbf{V}'(\lambda) V′(λ), deg V ′ ( λ ) < M \deg\mathbf{V}'(\lambda)<M degV′(λ)<M, 使得 A ′ ( λ ) = U ′ ( λ ) B ( λ ) + V ′ ( λ ) \mathbf{A}'(\lambda)=\mathbf{U}'(\lambda)\mathbf{B}(\lambda)+\mathbf{V}'(\lambda) A′(λ)=U′(λ)B(λ)+V′(λ). 进而有 A ( λ ) = [ A L B M − 1 λ L − M + U ′ ( λ ) ] B ( λ ) + V ′ ( λ ) \mathbf{A}(\lambda)=[\mathbf{A}_{L}\mathbf{B}^{-1}_{M}\lambda^{L-M}+\mathbf{U}'(\lambda)]\mathbf{B}(\lambda)+\mathbf{V}'(\lambda) A(λ)=[ALBM−1λL−M+U′(λ)]B(λ)+V′(λ). 定义 U ( λ ) = A L B M − 1 λ L − M + U ′ ( λ ) \mathbf{U}(\lambda)=\mathbf{A}_{L}\mathbf{B}^{-1}_{M}\lambda^{L-M}+\mathbf{U}'(\lambda) U(λ)=ALBM−1λL−M+U′(λ), V ( λ ) = V ′ ( λ ) \mathbf{V}(\lambda)=\mathbf{V}'(\lambda) V(λ)=V′(λ), 显然 U ( λ ) \mathbf{U}(\lambda) U(λ), V ( λ ) \mathbf{V}(\lambda) V(λ) 即为所求.
同理可证明: A ( λ ) \mathbf{A}(\lambda) A(λ) 和 B ( λ ) \mathbf{B}(\lambda) B(λ) 是 n n n 阶 λ \lambda λ-矩阵, 记 deg A ( λ ) = L \deg \mathbf{A}(\lambda)=L degA(λ)=L, deg B ( λ ) = M \deg \mathbf{B}(\lambda)=M degB(λ)=M, 有: L , M > 0 L, M \gt 0 L,M>0, 且 B M \mathbf{B}_{M} BM 可逆, 则存在 n n n 阶 λ \lambda λ-矩阵 U ( λ ) \mathbf{U}(\lambda) U(λ), V ( λ ) \mathbf{V}(\lambda) V(λ), deg V ( λ ) < M \deg\mathbf{V}(\lambda)<M degV(λ)<M, 使得 A ( λ ) = A ( λ ) U ( λ ) + V ( λ ) \mathbf{A}(\lambda)=\mathbf{A}(\lambda)\mathbf{U}(\lambda)+\mathbf{V}(\lambda) A(λ)=A(λ)U(λ)+V(λ).
相关文章:

λ-矩阵的多项式展开
原文链接 定义. 对于 m n m \times n mn 的 λ \lambda λ-矩阵 A ( λ ) [ a 11 ( λ ) . . . a 1 n ( λ ) ⋮ ⋮ a m 1 ( λ ) . . . a m n ( λ ) ] \mathbf{A}(\lambda)\begin{bmatrix} a_{11}(\lambda) & ... & a_{1n}(\lambda)\\ \vdots & & \vdo…...

如何在PDF 文件中删除页面?
查看不同的工具以及解释如何在 Windows、Android、macOS 和 iOS 上从 PDF 删除页面的步骤: PDF 是最难处理的文件格式之一。曾经有一段时间,除了阅读之外,无法用 PDF 做任何事情。但是今天,有许多应用程序和工具可以让您用它们做…...
)
蓝桥杯官网填空题(质数拆分)
问题描述 将 2022 拆分成不同的质数的和,请问最多拆分成几个? 答案提交 本题为一道结果填空的题,只需要算出结果后,在代码中使用输出语句将结果输出即可。 运行限制 import java.util.Scanner;public class Main {static int …...
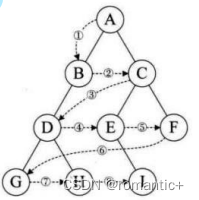
【数据结构】二叉树的顺序结构及链式结构
目录 1.树的概念及结构 1.1树的概念 1.2树的相关概念 编辑 1.3树的表示 1.4树在实际中的运用(表示文件系统的目录树结构) 2.二叉树概念及结构 2.1二叉树的概念 2.2现实中的二叉树 编辑 2.3特殊的二叉树 2.4二叉树的性质 2.5二叉树的存储结…...

海外IP代理:解锁网络边界的实战利器
文章目录 引言:正文:一、Roxlabs全球IP代理服务概览特点:覆盖范围:住宅IP真实性:性价比:在网络数据采集中的重要性: 二、实战应用案例一:跨境电商竞品分析步骤介绍:代码示…...

如何写好一个简历
如何编写求职简历 论Java程序员求职中简历的重要性 好简历的作用 在求职过程中,一份好的简历是非常重要的,它甚至可以直接决定能否被面试官认可。一份出色或者说是成功的个人简历,最根本的作用是能让看这份简历的人产生一定要见你的强烈愿…...
【AutoML】AutoKeras 进行 RNN 循环神经网络训练
由于最近这些天都在人工审查之前的哪些问答数据,所以迟迟都没有更新 AutoKeras 的训练结果。现在那部分数据都已经整理好了,20w 的数据最后能够使用的高质量数据只剩下 2k。这 2k 的数据已经经过数据校验并且对部分问题的提问方式和答案内容进行了不改变…...

H12-821_74
74.在某路由器上查看LSP,看到如下结果: A.发送目标地址为3.3.3.3的数据包时,打上标签1026,然后发送。 B.发送目标地址为4.4.4.4的数据包时,不打标签直接发送。 C.当路由器收到标签为1024的数据包,将把标签…...

有趣儿的组件(HTML/CSS)
分享几个炫酷的组件,起飞~~ 评论区留爪,继续分享哦~ 文章目录 1. 按钮2. 输入3. 工具提示4. 单选按钮5. 加载中 1. 按钮 HTML: <button id"btn">Button</button>CSS: button {padding: 10px 20px;text-tr…...
1、深度学习环境配置相关下载地址整理(cuda、cudnn、torch、miniconda、pycharm、torchvision等)
一、深度学习环境配置相关: 1、cuda:https://developer.nvidia.com/cuda-toolkit-archive 2、cudnn:https://developer.nvidia.com/rdp/cudnn-archive 4、miniconda:https://mirrors.tuna.tsinghua.edu.cn/anaconda/miniconda/?C…...
Spring Boot3自定义异常及全局异常捕获
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途。 目录 前置条件 目的 主要步骤 定义自定义异常类 创建全局异常处理器 手动抛出自定义异常 前置条件 已经初始化好一个…...
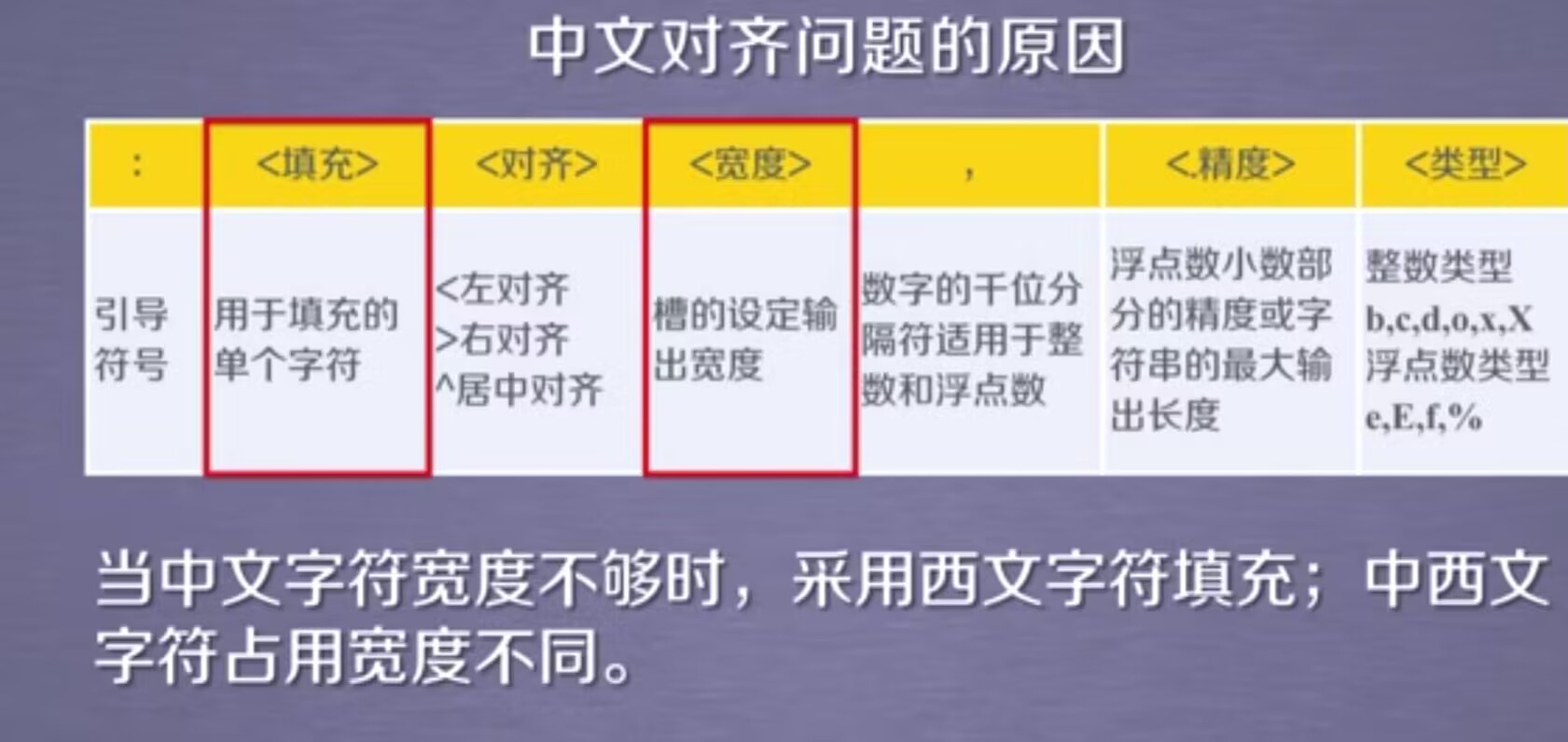
【python】网络爬虫与信息提取--Beautiful Soup库
Beautiful Soup网站:https://www.crummy.com/software/BeautifulSoup/ 作用:它能够对HTML.xml格式进行解析,并且提取其中的相关信息。它可以对我们提供的任何格式进行相关的爬取,并且可以进行树形解析。 使用原理:它能…...

谷歌浏览器,如何将常用打开的网站创建快捷方式到电脑桌面?
打开谷歌浏览器,打开想要创建的快捷方式的网页 点击浏览器右上角的三个点: 点击选择【更多工具】 选择【创建快捷方式】 然后,在浏览器上方会弹出一个框,让命名此创建的快捷方式的名称 命名好之后,再点击【创…...

产品经理面试题解析:业务架构是通往成功的关键吗?
大家好,我是小米!今天我要和大家聊的是产品经理面试中的一个热门话题:“业务架构”!相信不少小伙伴在准备面试的时候都会遇到这个问题,究竟什么是业务架构?它又与产品经理的工作有着怎样的关系呢࿱…...

【蓝桥杯】灭鼠先锋
一.题目描述 二.解题思路 博弈论: 只能转移到必胜态的,均为必败态。 可以转移到必败态的,均为必胜肽。 最优的策略是,下一步一定是必败态。 #include<iostream> #include<map> using namespace std;map<string,bo…...
)
2024年华为OD机试真题-求字符串中所有整数的最小和-Python-OD统一考试(C卷)
题目描述: 输入字符串s,输出s中包含所有整数的最小和 说明 1. 字符串s,只包含 a-z A-Z +- ; 2. 合法的整数包括 1) 正整数 一个或者多个0-9组成,如 0 2 3 002 102 2)负整数 负号 - 开头,数字部分由一个或者多个0-9组成,如 -0 -012 -23 -00023 输入描述: 包含…...
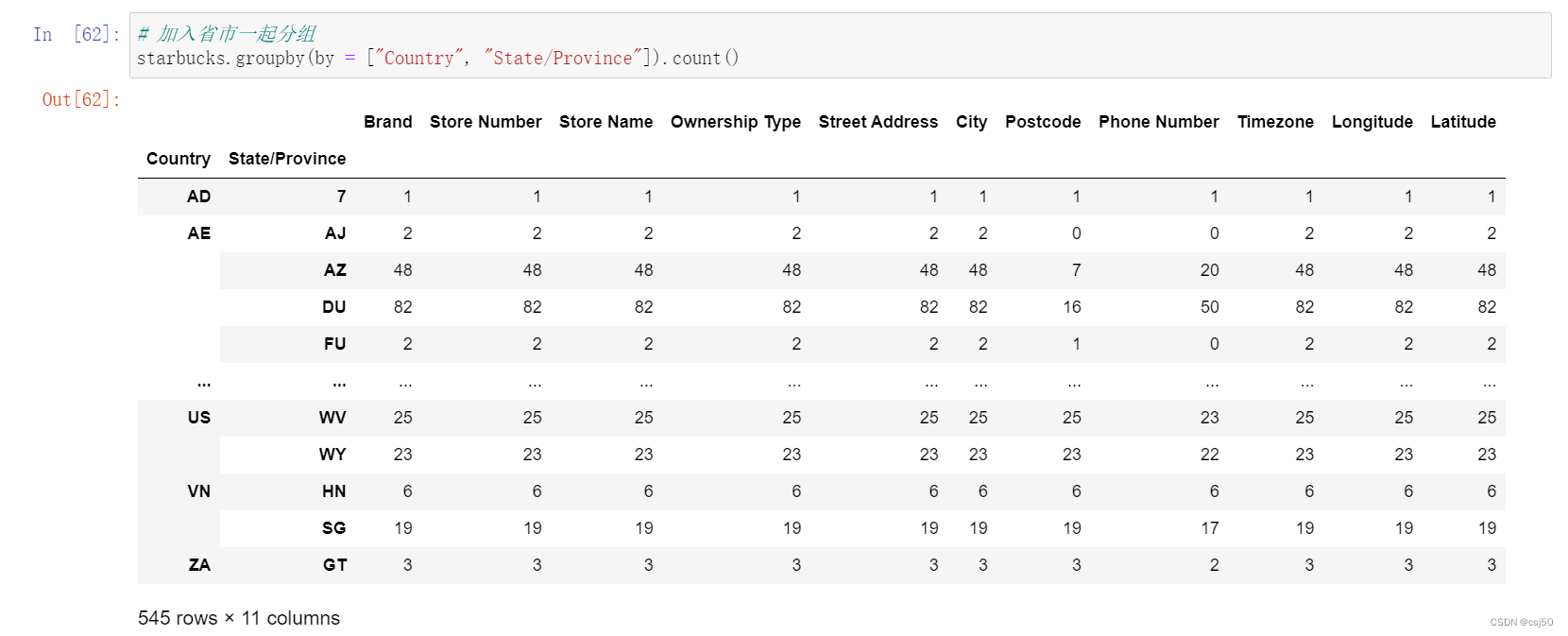
数据分析基础之《pandas(7)—高级处理2》
四、合并 如果数据由多张表组成,那么有时候需要将不同的内容合并在一起分析 1、先回忆下numpy中如何合并 水平拼接 np.hstack() 竖直拼接 np.vstack() 两个都能实现 np.concatenate((a, b), axis) 2、pd.concat([data1, data2], axis1) 按照行或者列…...

fluent脱硝SCR相对标准偏差、氨氮比、截面速度计算
# -*- coding: utf-8 -*- """ Created on Wed Sep 20 20:40:30 2023 联系QQ:3123575367,专业SCR脱硝仿真。 该程序用来处理fluent通过export-solution-ASCII-Space导出的数据,可计算标准偏差SD、相对标准偏差RSD,适用于求解平面的相对均匀…...
(A~E))
Codeforces Round 925 (Div. 3)(A~E)
题目暂时是AC,现在是Hack阶段,代码仅供参考。 A. Recovering a Small String 题目给出的n都可以由字母来组成,比如4可以是aab,字母里面排第一个和第二个,即1124。但是会歧义,比如aba为1214,也是…...

@RequestBody、@RequestParam、@RequestPart使用方式和使用场景
RequestBody和RequestParam和RequestPart使用方式和使用场景 1.RequestBody2.RequestParam3.RequestPart 1.RequestBody 使用此注解接收参数时,适用于请求体格式为 application/json,只能用对象接收 2.RequestParam 接收的参数是来自HTTP 请求体 或 请…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
