神经网络(Nature Network)
最近接触目标检测较多,再此对最基本的神经网络知识进行补充,本博客适合想入门人工智能、其含有线性代数及高等数学基础的人群观看
1.构成
由输入层、隐藏层、输出层、激活函数、损失函数组成。
- 输入层:接收原始数据
- 隐藏层:进行特征提取和转换
- 输出层:输出预测结果
- 激活函数:非线性变换
- 损失函数:衡量模型预测结果与真实值之间的差距
2.正向传播过程
基础的神经网络如下图所示,其中层1为输入层,层2为隐藏层,层3为输出层:

每一个圆圈代表了一个神经元,各层的神经元各自相连,如图中的绿色箭头。每一条相连的绿线上拥有起始设定好的权重。隐藏层的神经元后跟着激活函数,进行信号的转变。
对于每一层信号的输入输出,均有以下公式表达,X为此层的输入,O为此层的输出,一般输入层采用激活函数,即输入即为输出。
X = W ⋅ I n p u t O = s i g m o i d ( X ) X=W·Input\\ O=sigmoid(X) X=W⋅InputO=sigmoid(X)
I n p u t Input Input 为输入矩阵,此处以如下为例:
I n p u t = [ 1.0 0.5 0.35 ] Input = \begin{bmatrix} 1.0\\ 0.5\\ 0.35 \end{bmatrix} Input= 1.00.50.35
W W W 为权重矩阵,各层的权重各不相同
W = [ w 1.1 w 1.2 w 1.3 w 2.1 w 2.2 w 2.3 w 3.1 w 3.2 w 3.3 ] W= \begin{bmatrix} w_{1.1} & w_{1.2} &w_{1.3}\\ w_{2.1} & w_{2.2} &w_{2.3}\\ w_{3.1} & w_{3.2} &w_{3.3} \end{bmatrix} W= w1.1w2.1w3.1w1.2w2.2w3.2w1.3w2.3w3.3
s i g m o i d sigmoid sigmoid 为激活函数
y = 1 1 + e − x y=\frac{1}{1+e^{-x}} y=1+e−x1
过程演示(3层)
1.输入层: 由于输入层一般不使用激活函数,输入层的输出即为输入数据 I n p u t Input Input。
2.隐藏层: 此层的输入为:
X h i d d e n = W i n p u t 2 h i d d e n ⋅ I n p u t = [ w 1.1 w 1.2 w 1.3 w 2.1 w 2.2 w 2.3 w 3.1 w 3.2 w 3.3 ] ⋅ [ 1.0 0.5 0.35 ] X_{hidden}=W_{input2hidden} · Input= \begin{bmatrix} w_{1.1} & w_{1.2} &w_{1.3}\\ w_{2.1} & w_{2.2} &w_{2.3}\\ w_{3.1} & w_{3.2} &w_{3.3} \end{bmatrix} · \begin{bmatrix} 1.0\\ 0.5\\ 0.35 \end{bmatrix} Xhidden=Winput2hidden⋅Input= w1.1w2.1w3.1w1.2w2.2w3.2w1.3w2.3w3.3 ⋅ 1.00.50.35
此层的输出为:
O h i d d e n = s i g m o i d ( X h i d d e n ) = 1 1 + e X h i d d e n O_{hidden} = sigmoid(X_{hidden})=\frac{1}{1+e^{X_{hidden}}} Ohidden=sigmoid(Xhidden)=1+eXhidden1
3.输出层: 输出层永远不使用激活函数,输出层的输出即为输入,输出层的输入为:
X o u t p u t = W h i d d e n 2 o u t p u t ⋅ O h i d d e n X_{output} = W_{hidden2output}·O_{hidden} Xoutput=Whidden2output⋅Ohidden
3.激活函数
上文使用的是 s i g m o i d sigmoid sigmoid函数作为激活函数,还可以将其根据具体应用,更换为以下函数:
- Sigmoid函数:将输入值压缩到0到1之间,常用于二分类问题

- ReLU函数:将负值置为0,常用于深度神经网络中

- Tanh函数:将输入值压缩到-1到1之间,常用于回归问题

- Leaky ReLU函数:对负值进行微小的缩放,避免梯度消失问题

4.反向传播过程
误差计算:目标值-实际值 e n = t n − o n e_n = t_n - o_n en=tn−on
下面以单个神经元返回误差为例:

对于最后输出的误差我们需要将他根据前一层的权重传播到前一层,以上面单个神经元的反向传播过程为例。传回1号神经元的误差为 e r r o r s ⋅ w 1 w 1 + w 2 errors·\frac{w_1}{w_1+w_2} errors⋅w1+w2w1 ,传回2号神经元的误差为 e r r o r s ⋅ w 2 w 1 + w 2 errors·\frac{w_2}{w_1+w_2} errors⋅w1+w2w2 。
过程演示(3层)
下面我们把这个过程放到三层的神经网络中分析:

我们以第二层第一个神经元为例,分析误差传播到此的值。
e h i d d e n 1 = e o u t p u t 1 ⋅ w 1.1 w 1.1 + w 2.1 + w 3.1 + e o u t p u t 2 ⋅ w 1.2 w 1.2 + w 2.2 + w 3.2 + e o u t p u t 3 ⋅ w 1.3 w 1.3 + w 2.3 + w 3.3 e_{hidden1} = e_{output1}·\frac{w_{1.1}}{w_{1.1}+w_{2.1}+w_{3.1}}+e_{output2}·\frac{w_{1.2}}{w_{1.2}+w_{2.2}+w_{3.2}}+e_{output3}·\frac{w_{1.3}}{w_{1.3}+w_{2.3}+w_{3.3}} ehidden1=eoutput1⋅w1.1+w2.1+w3.1w1.1+eoutput2⋅w1.2+w2.2+w3.2w1.2+eoutput3⋅w1.3+w2.3+w3.3w1.3
接下来我们使用矩阵来表达这个麻烦的公式:
输出层误差:
e r r o r o u t p u t = ( e 1 e 2 e 3 ) error_{output}=\begin{pmatrix} e_1\\ e_2\\ e_3 \end{pmatrix} erroroutput= e1e2e3
隐藏层误差:
e r r o r h i d d e n = [ w 1.1 w 1.1 + w 2.1 + w 3.1 w 1.2 w 1.2 + w 2.2 + w 3.2 w 1.3 w 1.3 + w 2.3 + w 3.3 w 2.1 w 1.1 + w 2.1 + w 3.1 w 2.2 w 1.2 + w 2.2 + w 3.2 w 2.3 w 1.3 + w 2.3 + w 3.3 w 3.1 w 1.1 + w 2.1 + w 3.1 w 3.2 w 1.2 + w 2.2 + w 3.2 w 3.3 w 1.3 + w 2.3 + w 3.3 ] ⋅ e r r o r o u t p u t error_{hidden}=\begin{bmatrix} \frac{w_{1.1}}{w_{1.1}+w_{2.1}+w_{3.1}} &\frac{w_{1.2}}{w_{1.2}+w_{2.2}+w_{3.2}} &\frac{w_{1.3}}{w_{1.3}+w_{2.3}+w_{3.3}}\\ \frac{w_{2.1}}{w_{1.1}+w_{2.1}+w_{3.1}} &\frac{w_{2.2}}{w_{1.2}+w_{2.2}+w_{3.2}} &\frac{w_{2.3}}{w_{1.3}+w_{2.3}+w_{3.3}}\\ \frac{w_{3.1}}{w_{1.1}+w_{2.1}+w_{3.1}} &\frac{w_{3.2}}{w_{1.2}+w_{2.2}+w_{3.2}} &\frac{w_{3.3}}{w_{1.3}+w_{2.3}+w_{3.3}}\\ \end{bmatrix} · error_{output} errorhidden= w1.1+w2.1+w3.1w1.1w1.1+w2.1+w3.1w2.1w1.1+w2.1+w3.1w3.1w1.2+w2.2+w3.2w1.2w1.2+w2.2+w3.2w2.2w1.2+w2.2+w3.2w3.2w1.3+w2.3+w3.3w1.3w1.3+w2.3+w3.3w2.3w1.3+w2.3+w3.3w3.3 ⋅erroroutput
去归一化:
e r r o r h i d d e n = [ w 1.1 w 1.2 w 1.3 w 2.1 w 2.2 w 2.3 w 3.1 w 3.2 w 3.3 ] ⋅ e r r o r o u t p u t = w h i d d e n 2 o u t p u t ⋅ e r r o r o u t p u t error_{hidden}=\begin{bmatrix} w_{1.1} & w_{1.2} & w_{1.3}\\ w_{2.1} & w_{2.2} & w_{2.3}\\ w_{3.1} & w_{3.2} & w_{3.3} \end{bmatrix} · error_{output} = w_{hidden2output}·error_{output} errorhidden= w1.1w2.1w3.1w1.2w2.2w3.2w1.3w2.3w3.3 ⋅erroroutput=whidden2output⋅erroroutput
5.更新权重
下一步需要取得误差最小的权重作为最优权重,在此我们使用梯度下降的方法找到误差最小时的权重。
梯度下降: 用于计算函数的最小值。随机起始点,通过导数的正负判断方向,朝着函数减小的方向,一步步增加x,并计算他的导数当导数为零或为设定范围内,取得最小值;否则继续增加。
在神经网络中由于x为权重矩阵,我们使用的梯度下降为多维梯度下降。
设定误差函数
在此例中我们使用 E = ( t n − o n ) 2 E = (t_n-o_n)^2 E=(tn−on)2
误差函数的斜率
∂ E ∂ w i j = ∂ ∂ w i j ∑ n ( t n − o n ) 2 \frac{\partial E}{\partial w_{ij}}=\frac{\partial}{\partial w_{ij}}\sum_n(t_n-o_n)^2 ∂wij∂E=∂wij∂n∑(tn−on)2
由于在这里 o n o_n on 仅取决于连接着的权重,所以误差函数的斜率可以改写为:
∂ ∂ w i j ( t n − o n ) 2 \frac{\partial}{\partial w_{ij}}(t_n-o_n)^2 ∂wij∂(tn−on)2
根据导数的链式法则,我们改写斜率函数:
∂ E ∂ w i j = ∂ E ∂ o n × ∂ o n ∂ w i j = − 2 ( t n − o n ) ∂ o n ∂ w i j \frac{\partial E}{\partial w_{ij}}=\frac{\partial E}{\partial o_n}\times \frac{\partial o_n}{\partial w_{ij}}=-2(t_n-o_n)\frac{\partial o_n}{\partial w_{ij}} ∂wij∂E=∂on∂E×∂wij∂on=−2(tn−on)∂wij∂on
我们再将 o n o_n on带入到此函数 o n = s i g m o i d ( ∑ j w j , k ⋅ o j ) o_n=sigmoid(\sum_j w_{j,k}·o_j) on=sigmoid(∑jwj,k⋅oj), o j o_j oj为前一层的输出,得到函数如下:
斜率函数 = − 2 ( t n − o n ) ∂ ∂ w i , j s i g m o i d ( ∑ j w j k ⋅ o j ) 斜率函数 = -2(t_n-o_n)\frac{\partial}{\partial w_{i,j}}sigmoid(\sum_j w_{jk}·o_j) 斜率函数=−2(tn−on)∂wi,j∂sigmoid(j∑wjk⋅oj)
我们对sigmoid函数进行微分:
∂ s i g m o i d ( x ) ∂ x = s i g m o i d ( x ) ( 1 − s i g m o i d ( x ) ) \frac{\partial sigmoid(x)}{\partial x} = sigmoid(x)(1-sigmoid(x)) ∂x∂sigmoid(x)=sigmoid(x)(1−sigmoid(x))
我们再把它放到斜率函数之中:
斜率函数 = − 2 ⋅ ( t n − o n ) ⋅ s i g m o i d ( ∑ j w j k ⋅ o j ) ⋅ ( 1 − ∑ j w j k ⋅ o j ) ⋅ ∂ ∂ w i . j ( ∑ j w j k ⋅ o j ) = − 2 ⋅ ( t n − o n ) ⋅ s i g m o i d ( ∑ j w j k ⋅ o j ) ⋅ ( 1 − ∑ j w j k ⋅ o j ) ⋅ o j 斜率函数=-2·(t_n-o_n)·sigmoid(\sum_jw_{jk}·o_j)·(1-\sum_jw_{jk}·o_j)·\frac{\partial }{\partial w_{i.j}}(\sum_jw_{jk}·o_j)\\ =-2·(t_n-o_n)·sigmoid(\sum_jw_{jk}·o_j)·(1-\sum_jw_{jk}·o_j)·o_j 斜率函数=−2⋅(tn−on)⋅sigmoid(j∑wjk⋅oj)⋅(1−j∑wjk⋅oj)⋅∂wi.j∂(j∑wjk⋅oj)=−2⋅(tn−on)⋅sigmoid(j∑wjk⋅oj)⋅(1−j∑wjk⋅oj)⋅oj
由于在此过程中我们只需判断斜率方向,我们可以把常数去除,即:
斜率函数 = − ( t n − o n ) ⋅ s i g m o i d ( ∑ j w j k ⋅ o j ) ⋅ ( 1 − ∑ j w j k ⋅ o j ) ⋅ o j 斜率函数=-(t_n-o_n)·sigmoid(\sum_jw_{jk}·o_j)·(1-\sum_jw_{jk}·o_j)·o_j 斜率函数=−(tn−on)⋅sigmoid(j∑wjk⋅oj)⋅(1−j∑wjk⋅oj)⋅oj
我们根据已有的关系对斜率在此修改:
- ( t n − o n ) (t_n - o_n) (tn−on) 为 ( 目标值 − 实际值 ) (目标值-实际值) (目标值−实际值),即 e i e_i ei
- ∑ i w i , j ⋅ o i \sum_i w_{i,j}·o_i ∑iwi,j⋅oi 为进入上一层的输入
- o i o_i oi 为上一层的输出
∂ E ∂ w i j = − e i ⋅ s i g m o i d ( ∑ i w i j o i ) ⋅ ( 1 − s i g m o i d ( ∑ i w i j o i ) ) ⋅ o i \frac{\partial E}{\partial w_{ij}}=-e_i \cdot sigmoid(\sum_i w_{ij}o_i)\cdot (1-sigmoid(\sum_i w_{ij}o_i))\cdot o_i ∂wij∂E=−ei⋅sigmoid(i∑wijoi)⋅(1−sigmoid(i∑wijoi))⋅oi
更新权重
有了误差函数的斜率,我们就可以通过梯度下降的方式更新权重,其中 α \alpha α为设定好的学习率:
W n e w = W o l d − α ∂ E ∂ w i j W_{new} = W_{old}-\alpha \frac{\partial E}{\partial w_{ij}} Wnew=Wold−α∂wij∂E
权重的矩阵变化
Δ w i j = α ⋅ E k ⋅ o k ⋅ ( 1 − o k ) ⋅ o j \Delta w_{ij} = \alpha \cdot E_k \cdot o_k \cdot (1-o_k) \cdot o_j Δwij=α⋅Ek⋅ok⋅(1−ok)⋅oj
6.代码实现
神经网络代码应该由三部分组成:初始化函数、训练函数、查询函数
- 初始化函数:应该包含各层的节点数,学习率,随机权重矩阵以及激活函数
- 训练函数:应该包含正、反向传播,权重更新
- 查询函数:正向传播过程
import numpy.random
import scipy.special# 激活函数设置
def activation_function(x):return scipy.special.expit(x)# 神经网络类
class NeuralNetwork:# 初始化函数def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate):# 输入层、隐含层、输出层节点数self.inodes = inputnodesself.hnodes = hiddennodesself.onodes = outputnodes# 学习率self.lr = learningrate# 随机权重矩阵self.Wih = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes))self.Who = numpy.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes))# 激活函数self.activation_function = activation_functionpass# 训练函数def train(self, inputs_list, targets_list):# 输入的目标list改为2D数组targets = numpy.array(targets_list, ndmin=2).T# 第一步计算结果(与query一致)inputs = numpy.array(inputs_list, ndmin=2).Thidden_inputs = numpy.dot(self.Wih, inputs)hidden_outputs = self.activation_function(hidden_inputs)final_inputs = numpy.dot(self.Who, hidden_outputs)final_outputs = self.activation_function(final_inputs)# 计算输出层误差 error_output = 目标值 - 测量值output_errors = targets - final_outputs# 计算隐含层误差 errors_hidden = w_hidden2output^T · errors_outputhidden_errors = numpy.dot(self.Who.T, output_errors)# 权重更新self.Who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)),numpy.transpose(hidden_outputs))self.Wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)),numpy.transpose(inputs))pass# 查询函数def query(self, inputs_list):# 输入的list改为2D数组inputs = numpy.array(inputs_list, ndmin=2).T# 隐含层的输入 hidden_inputs = w_input2hedden · inputshidden_inputs = numpy.dot(self.Wih, inputs)# 隐含层的输出 hidden_outputs = sigmoid(hidden_inputs)hidden_outputs = self.activation_function(hidden_inputs)# 输出层的输入final_inputs = numpy.dot(self.Who, hidden_outputs)# 输出层的输出final_outputs = self.activation_function(final_inputs)return final_outputs
相关文章:

神经网络(Nature Network)
最近接触目标检测较多,再此对最基本的神经网络知识进行补充,本博客适合想入门人工智能、其含有线性代数及高等数学基础的人群观看 1.构成 由输入层、隐藏层、输出层、激活函数、损失函数组成。 输入层:接收原始数据隐藏层:进行…...
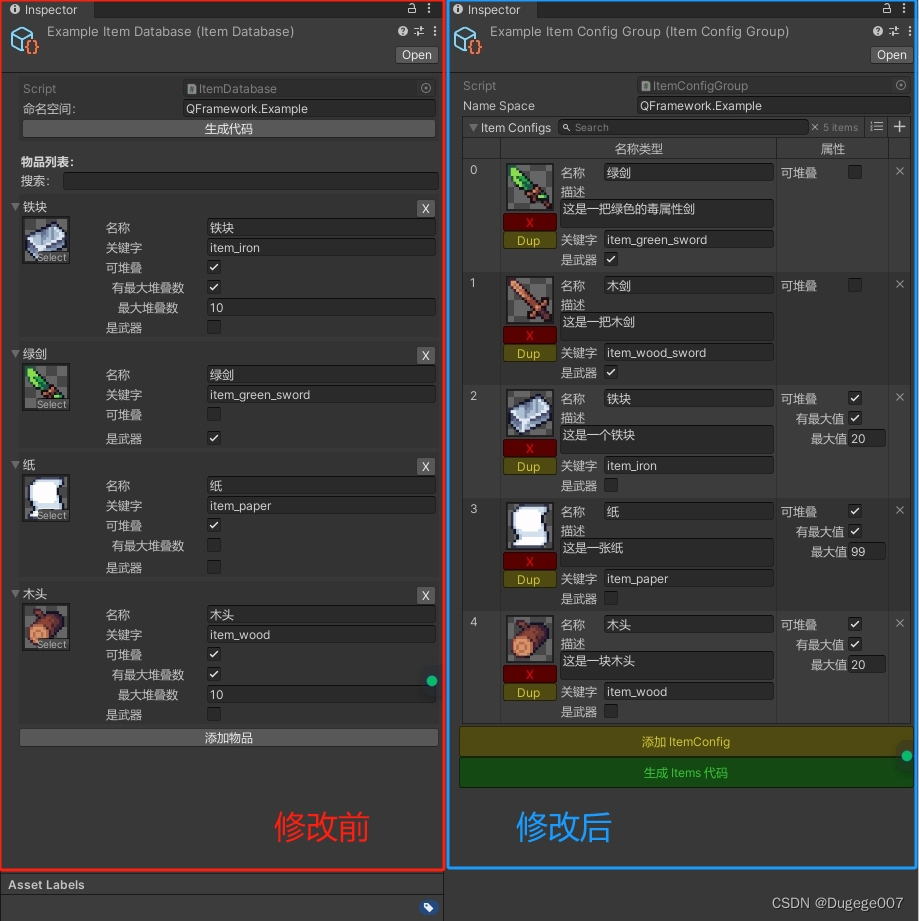
【Unity】QFramework通用背包系统优化:使用Odin优化编辑器
前言 在学习凉鞋老师的课程《QFramework系统设计:通用背包系统》第四章时,笔者使用了Odin插件,对Item和ItemDatabase的SO文件进行了一些优化,使物品页面更加紧凑、更易拓展。 核心逻辑和功能没有改动,整体代码量减少…...

基本算法--贪心
1.简述 贪心法的效率非常高,复杂度常常为O(1),是一种局部最优的解题方法,而很多问题都需要求全局最优,,所以在使用贪心法之前需要评估是否能从局部最优推广到全局最优。 2.思路 作为算法的贪…...
13. 串口接收模块的项目应用案例
1. 使用串口来控制LED灯工作状态 使用串口发送指令到FPGA开发板,来控制第7课中第4个实验的开发板上的LED灯的工作状态。 LED灯的工作状态:让LED灯按指定的亮灭模式亮灭,亮灭模式未知,由用户指定,8个变化状态为一个循…...

Python re找到特定pattern并将此pattern重复n次
要找到字符串s中的数字,并将这些数字重复3次: import re s "abc123def456ghi789" # 找到所有的数字 numbers re.findall(r\d, s) # 重复每个数字3次 repeated_numbers [num * 3 for num in numbers] # 将重复的数字放回原位置 #…...
ChatGpt报错:We ran into an issue while authenticating you解决办法
在登录ChatGpt时报错:Oops!,We ran into an issue while authenticating you.(我们在验证您时遇到问题),记录一下解决过程。 完整报错: We ran into an issue while authenticating you. If this issue persists, please contact…...

如何从 iPhone 恢复已删除的视频:简单有效方法
无论您是在尝试释放空间时不小心删除了 iPhone 上的视频,还是在出厂时清空了手机,现在所有数据都消失了,都不要放弃。有一些方法可以恢复这些视频。 在本文中,我们将向您展示六种最有效的数据恢复方法,可以帮助您从 i…...

【python量化交易】qteasy使用教程02 - 获取和管理金融数据
qteasy教程2 - 获取并管理金融数据 qteasy教程2 - 获取并管理金融数据开始前的准备工作获取基础数据以及价格数据下载交易日历和基础数据查看股票和指数的基础数据下载沪市股票数据从本地获取股价数据生成K线图 数据类型的查找定期下载数据到本地回顾总结 qteasy教程2 - 获取并…...
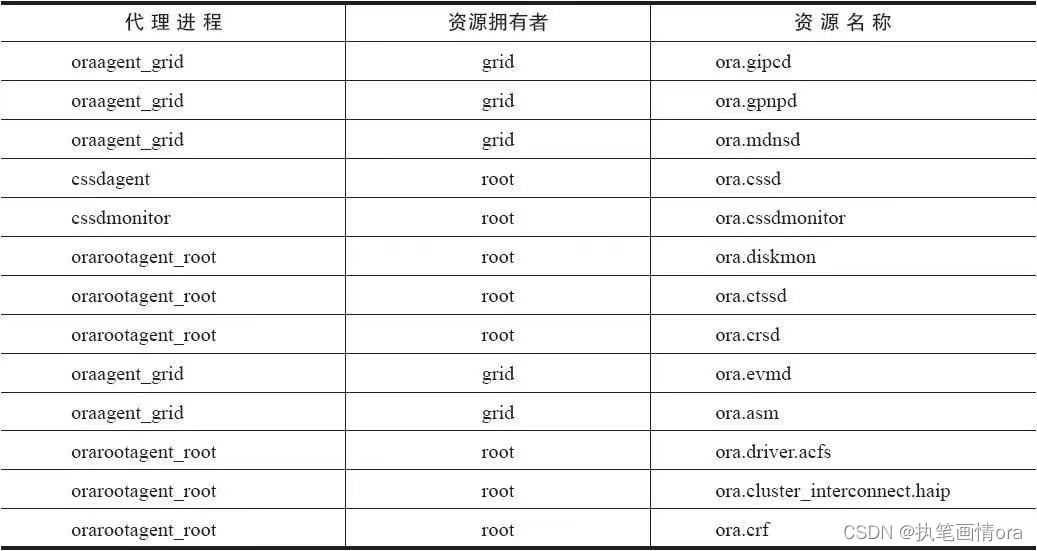
数据库学习案例20240206-ORACLE NEW RAC agent and resource关系汇总。
1 集群架构图 整体集群架构图如下: 1 数据库启动顺序OHASD层面 操作系统进程init.ohasd run启动ohasd.bin init.ohasd run 集群自动启动是否被禁用 crsctl enable has/crsGIHOME所在文件系统是否被正常挂载。管道文件npohasd是否能够被访问, cd /var/t…...
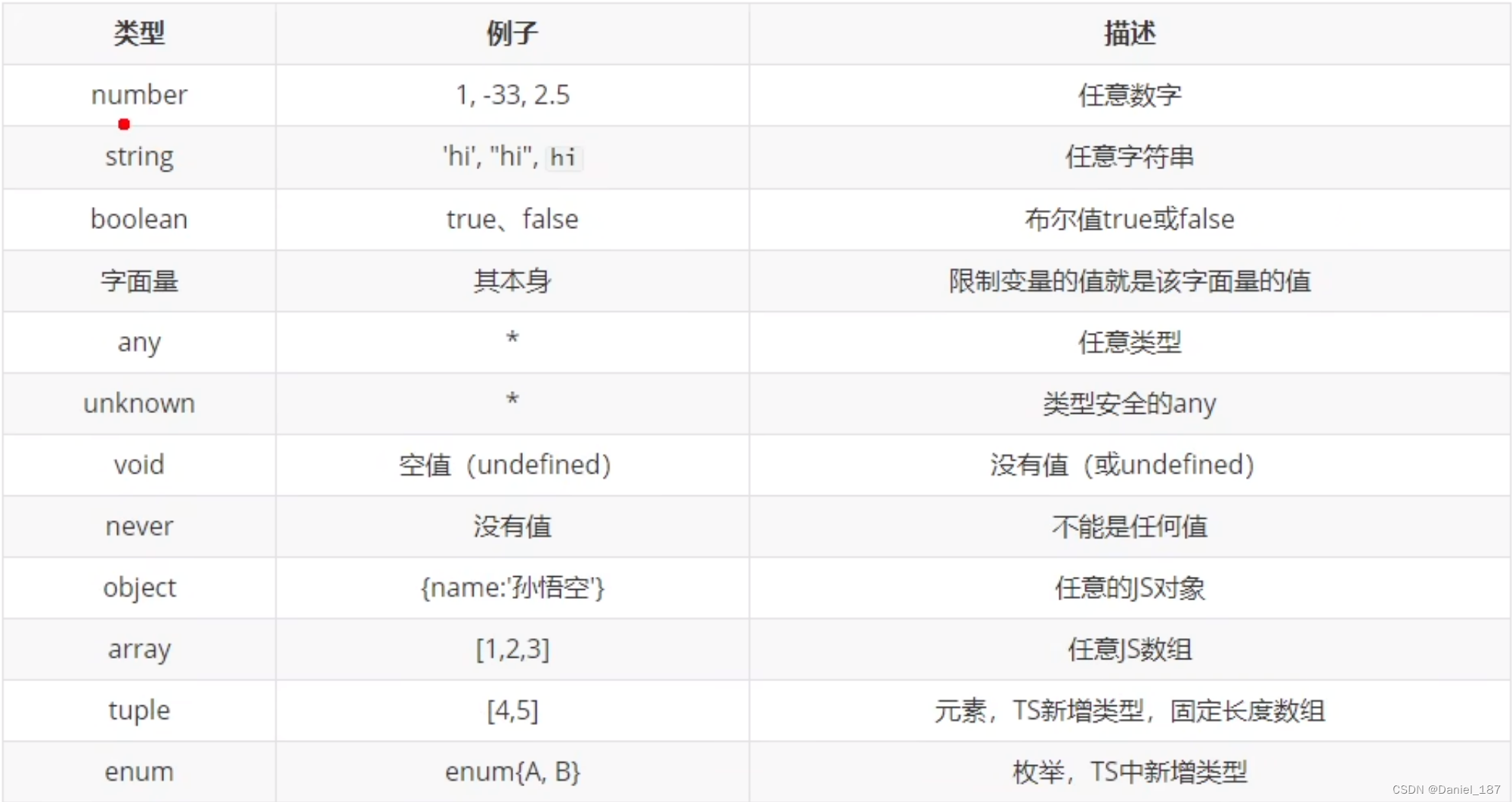
TypeScript 入门
课程地址 ts 开发环境搭建 npm i -g typescript查看安装位置: $ npm root -g C:\Users\Daniel\AppData\Roaming\npm\node_modules创建 hello.ts: console.log("hello, ts");编译 ts 文件,得到 js 文件: $ tsc foo.…...

linux 磁盘相关操作
1.U盘接入虚拟机 (1)在插入u盘时,虚拟机会检测usb设备,在弹出窗口选择连接到虚拟机即可。 (2)或 直接在虚拟机--->可移动设备--->找到U盘---->连接 2.检测U盘是否被虚拟机识别 ls /dev/sd* 查…...
函数详解)
PyTorch: torch.max()函数详解
torch.max函数详解:基于PyTorch的深入探索 🌵文章目录🌵 🌳引言🌳🌳torch.max()函数简介🌳🌳torch.max()的返回值🌳🌳torch.max()的应用示例🌳&am…...
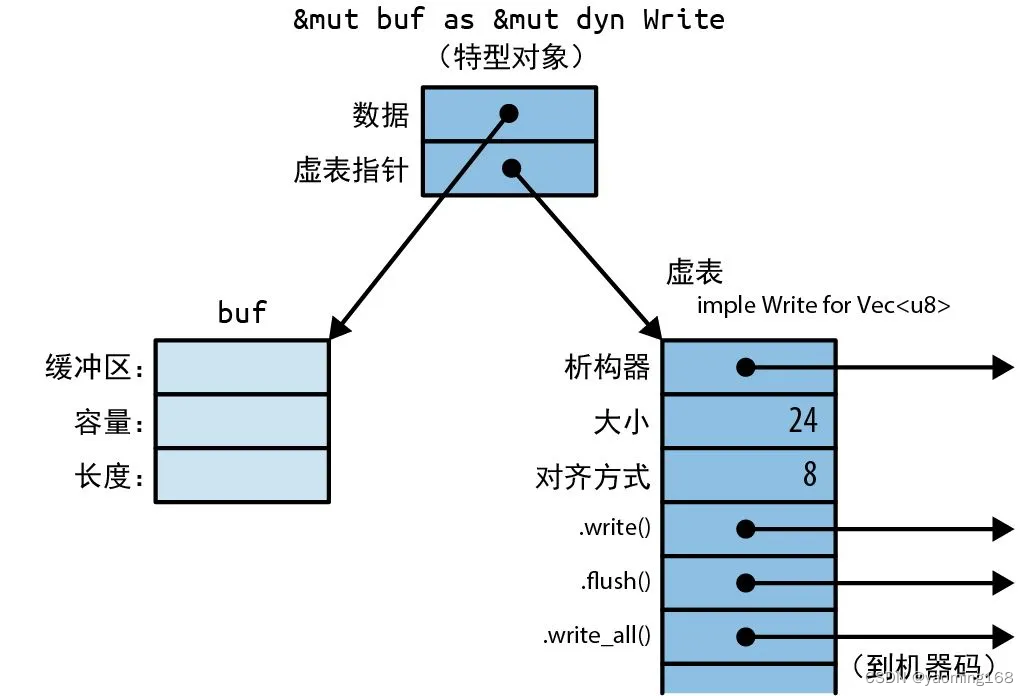
Rust基础拾遗--核心功能
Rust基础拾遗 前言1.所有权与移动1.1 所有权 2.引用3.特型与泛型简介3.1 使用特型3.2 特型对象3.3 泛型函数与类型参数 4.实用工具特型5.闭包 前言 通过Rust程序设计-第二版笔记的形式对Rust相关重点知识进行汇总,读者通读此系列文章就可以轻松的把该语言基础捡起来…...
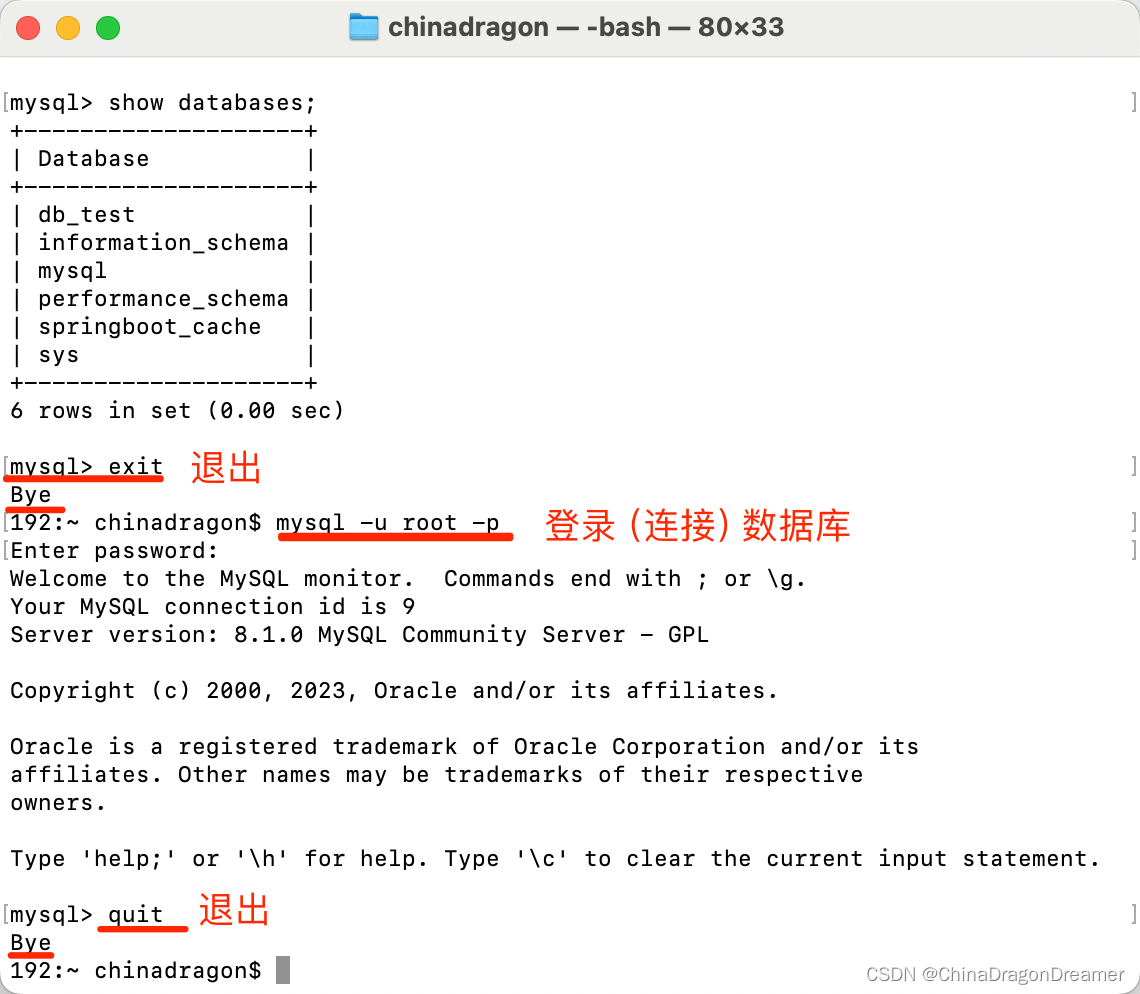
MySQL:常用指令
MySQL官网 一、在Windows 系统 cmd窗口里执行的命令 启动:net start MySQL停止:net stop MySQL卸载:sc delete MySQL 二、在macOS系统终端里执行的命令 启动:mysql.server start停止:mysql.server stop重启:mysql.server restart 三、执行帮…...

Scrapy:Python中强大的网络爬虫框架
Scrapy:Python中强大的网络爬虫框架 在当今信息爆炸的时代,从互联网上获取数据已经成为许多应用程序的核心需求。Scrapy是一款基于Python的强大网络爬虫框架,它提供了一种灵活且高效的方式来提取、处理和存储互联网上的数据。本文将介绍Scrap…...

linux系统非关系型数据库redis的配置文件
redis配置文件 Redis的配置文件位于Redis安装目录下,文件名为redis.conf,配置项说明如下 Redis默认不是以守护进程的方式运行,可以通过该配置项修改,使用yes启用守护进程 daemonize no当Redis以守护进程方式运行时,Red…...
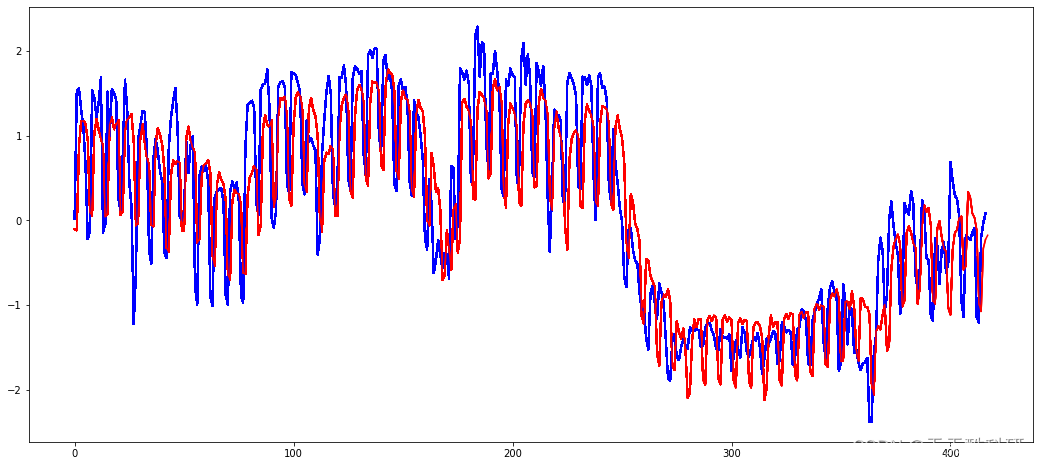
电力负荷预测 | 基于LSTM、TCN的电力负荷预测(Python)
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 电力负荷预测 | 基于LSTM、TCN的电力负荷预测(Python) 源码设计 #------------------...

Java+SpringBoot实习管理系统探秘
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...

c入门第十六篇——学生成绩管理系统
师弟:“师兄,我最近构建了一个学生成绩管理系统,有空试用一下么?” 我:“好啊!” 一个简单的学生成绩管理系统,基本功能包括:添加学生信息、显示所有学生信息、按学号查找学生信息、…...
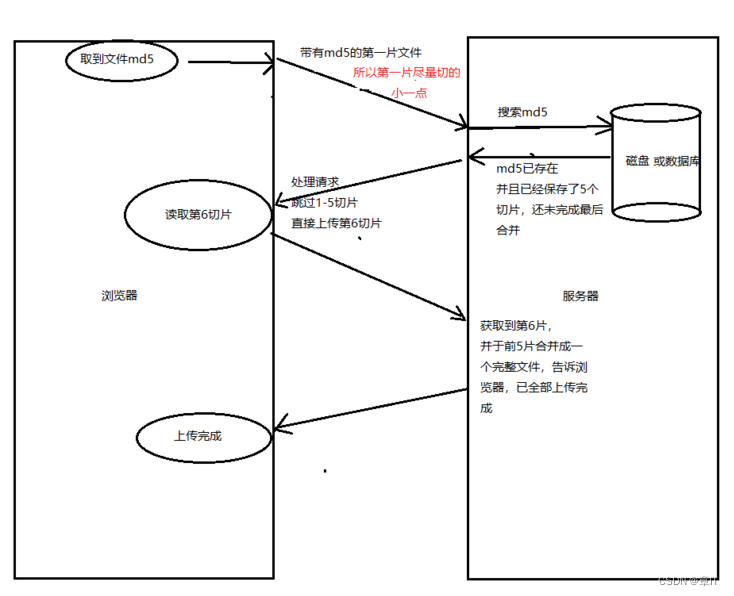
大文件上传如何做断点续传?
文章目录 一、是什么分片上传断点续传 二、实现思路三、使用场景小结 参考文献 一、是什么 不管怎样简单的需求,在量级达到一定层次时,都会变得异常复杂 文件上传简单,文件变大就复杂 上传大文件时,以下几个变量会影响我们的用…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
