机器学习--K-近邻算法常见的几种距离算法详解
文章目录
- 距离度量
- 1 欧式距离(Euclidean Distance)
- 2 曼哈顿距离(Manhattan Distance)
- 3 切比雪夫距离 (Chebyshev Distance)
- 4 闵可夫斯基距离(Minkowski Distance)
- 5 标准化欧氏距离 (Standardized EuclideanDistance)
- 6 余弦距离(Cosine Distance)
- 7 汉明距离(Hamming Distance)【了解】
- 8 杰卡德距离(Jaccard Distance)【了解】
- 9 马氏距离(Mahalanobis Distance)【了解】
- 10 “连续属性”和“离散属性”的距离计算
距离度量
距离公式的基本性质
在机器学习过程中,对于函数dist(…),若它是一"距离度量"(distance measure),则需要满足一些基本性质

1 欧式距离(Euclidean Distance)
欧氏距离是最容易直观理解的距离度量方法,我们小学、初中和高中接触到的两个点在空间中的距离一般都是指欧氏距离。

举例:
X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 1.4142 2.8284 4.2426 1.4142 2.8284 1.4142
2 曼哈顿距离(Manhattan Distance)
在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。
这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。
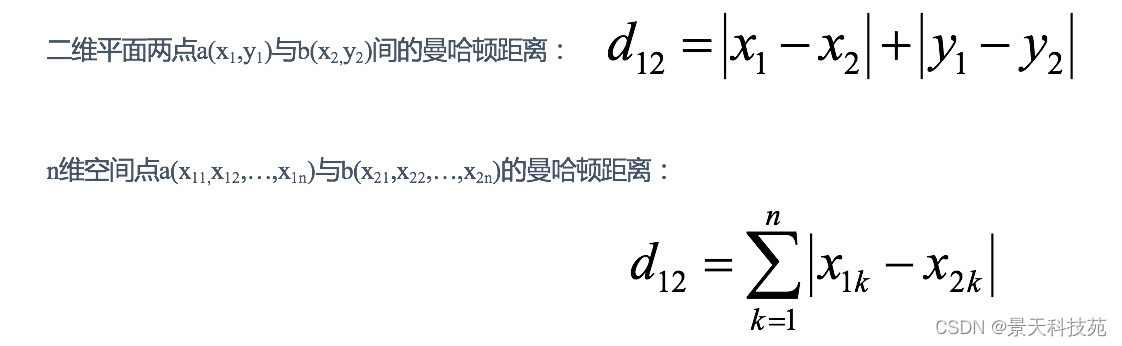
举例:
X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 2 4 6 2 4 2
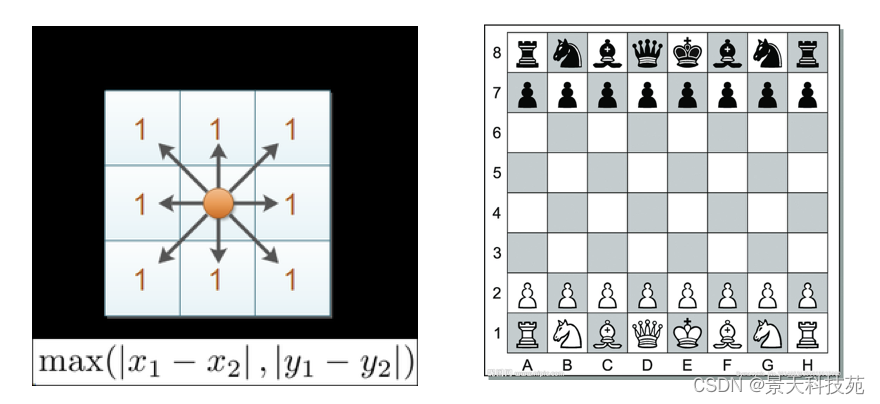
3 切比雪夫距离 (Chebyshev Distance)
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。
国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
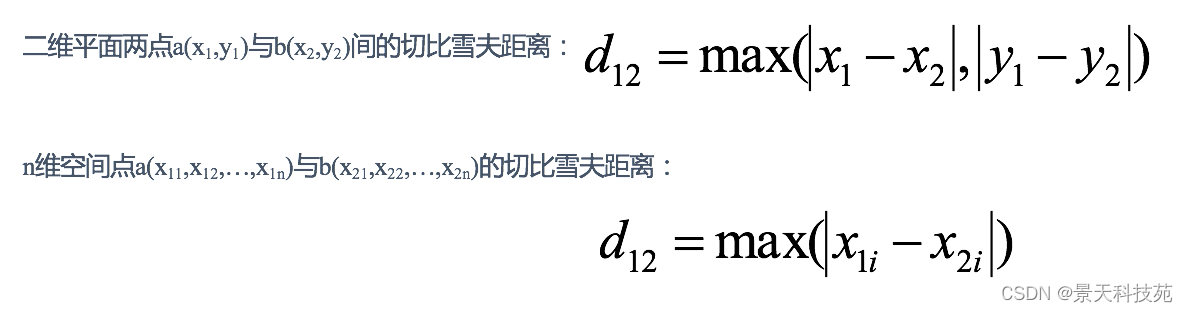
举例:
X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 1 2 3 1 2 1
4 闵可夫斯基距离(Minkowski Distance)
闵氏距离不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述。
两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为:
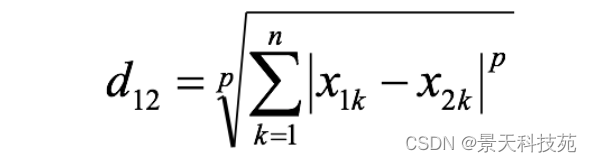
其中p是一个变参数:
当p=1时,就是曼哈顿距离;
当p=2时,就是欧氏距离;
当p→∞时,就是切比雪夫距离。
根据p的不同,闵氏距离可以表示某一类/种的距离。
小结:
1 闵氏距离,包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点:
e.g. 二维样本(身高[单位:cm],体重[单位:kg]),现有三个样本:a(180,50),b(190,50),c(180,60)。
a与b的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c的闵氏距离。但实际上身高的10cm并不能和体重的10kg划等号。
2 闵氏距离的缺点:
(1)将各个分量的量纲(scale),也就是“单位”相同的看待了;
(2)未考虑各个分量的分布(期望,方差等)可能是不同的。
5 标准化欧氏距离 (Standardized EuclideanDistance)
标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。思路:既然数据各维分量的分布不一样,那先将各个分量都“标准化”到均值、方差相等。 $S_k$表示各个维度的标准差
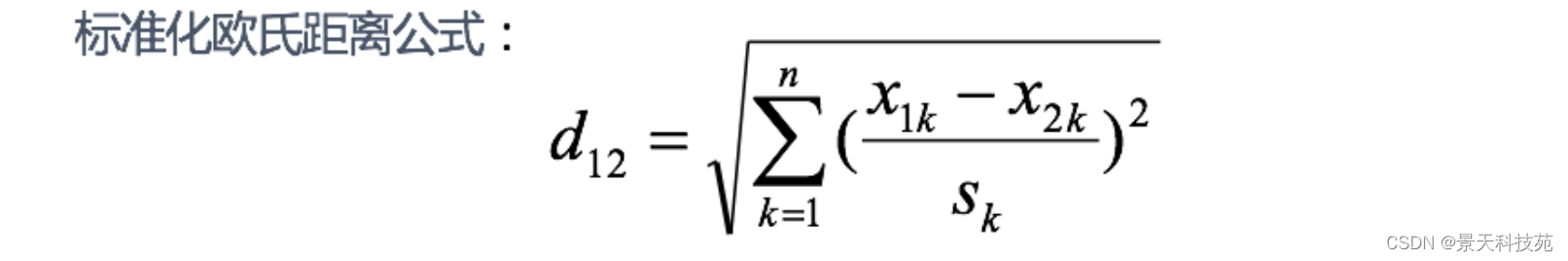
如果将方差的倒数看成一个权重,也可称之为加权欧氏距离(Weighted Euclidean distance)。
举例:
X=[[1,1],[2,2],[3,3],[4,4]];(假设两个分量的标准差分别为0.5和1)
经计算得:
d = 2.2361 4.4721 6.7082 2.2361 4.4721 2.2361
6 余弦距离(Cosine Distance)
几何中,夹角余弦可用来衡量两个向量方向的差异;机器学习中,借用这一概念来衡量样本向量之间的差异。
二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式:
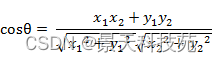
两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为:
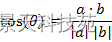
即:
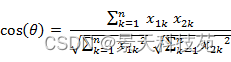
夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小,余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1,当两个向量的方向完全相反余弦取最小值-1。
举例:
X=[[1,1],[1,2],[2,5],[1,-4]]
经计算得:
d = 0.9487 0.9191 -0.5145 0.9965 -0.7593 -0.8107
7 汉明距离(Hamming Distance)【了解】
两个等长字符串s1与s2的汉明距离为:将其中一个变为另外一个所需要作的最小字符替换次数。用在NLP中比较多
例如:
The Hamming distance between “1011101” and “1001001” is 2.
The Hamming distance between “2143896” and “2233796” is 3.
The Hamming distance between “toned” and “roses” is 3.
汉明重量:是字符串相对于同样长度的零字符串的汉明距离,也就是说,它是字符串中非零的元素个数:对于二进制字符串来说,就是 1 的个数,所以 11101 的汉明重量是 4。因此,如果向量空间中的元素a和b之间的汉明距离等于它们汉明重量的差a-b。
应用:汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中,为了增强容错性,应使得编码间的最小汉明距离尽可能大。但是,如果要比较两个不同长度的字符串,不仅要进行替换,而且要进行插入与删除的运算,在这种场合下,通常使用更加复杂的编辑距离等算法。
举例:
X=[[0,1,1],[1,1,2],[1,5,2]]
注:以下计算方式中,把2个向量之间的汉明距离定义为2个向量不同的分量所占的百分比。
经计算得:
d = 0.6667 1.0000 0.3333
8 杰卡德距离(Jaccard Distance)【了解】
杰卡德相似系数(Jaccard similarity coefficient):两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示:
在推荐系统里面用的比较多
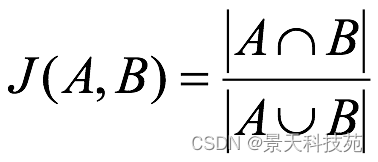
杰卡德距离(Jaccard Distance):与杰卡德相似系数相反,用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度:
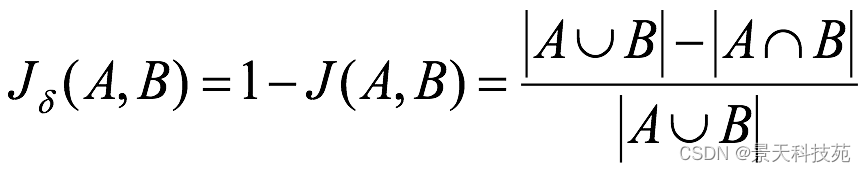
举例:
X=[[1,1,0][1,-1,0],[-1,1,0]]
注:以下计算中,把杰卡德距离定义为不同的维度的个数占“非全零维度”的比例
经计算得:
d = 0.5000 0.5000 1.0000
9 马氏距离(Mahalanobis Distance)【了解】
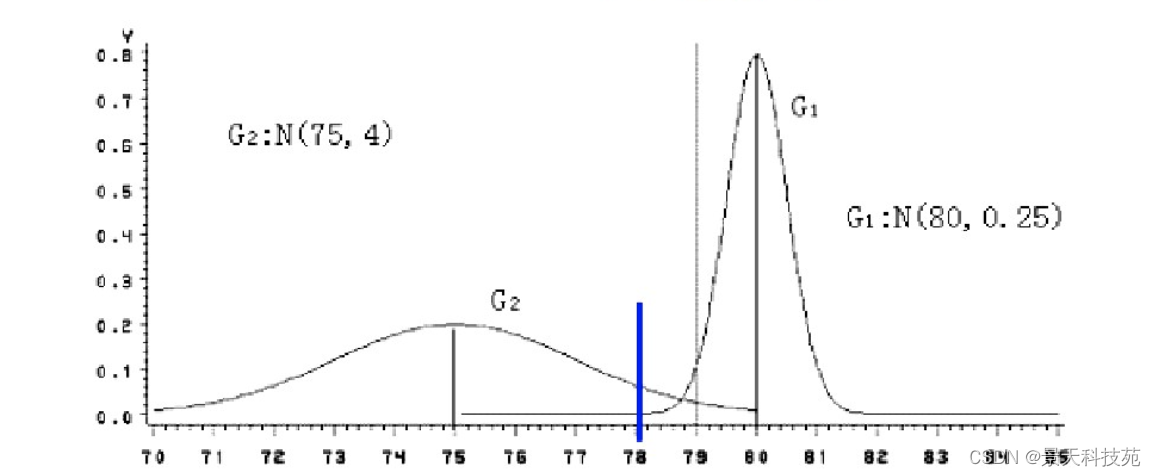
下图有两个正态分布图,它们的均值分别为a和b,但方差不一样,则图中的A点离哪个总体更近?或者说A有更大的概率属于谁?显然,A离左边的更近,A属于左边总体的概率更大,尽管A与a的欧式距离远一些。这就是马氏距离的直观解释。
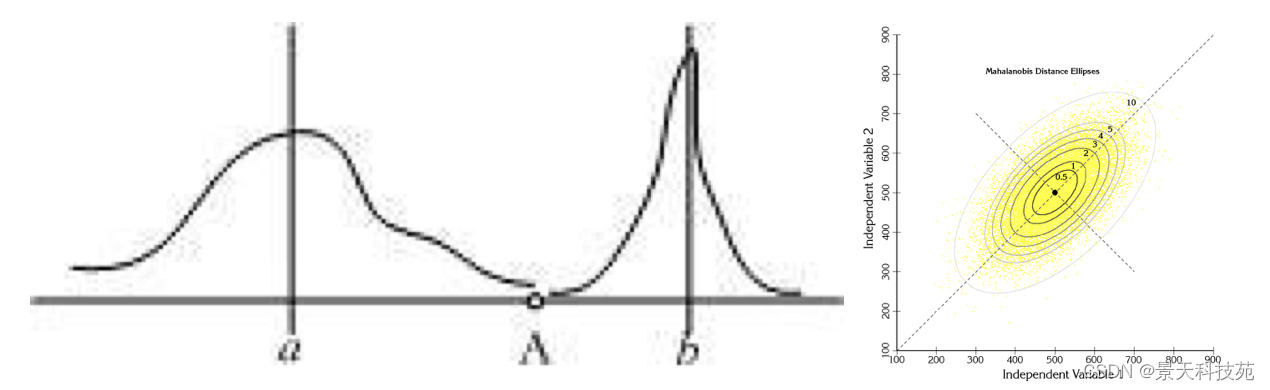
马氏距离是基于样本分布的一种距离。
马氏距离是由印度统计学家马哈拉诺比斯提出的,表示数据的协方差距离。它是一种有效的计算两个位置样本集的相似度的方法。
与欧式距离不同的是,它考虑到各种特性之间的联系,即独立于测量尺度。
马氏距离定义:设总体G为m维总体(考察m个指标),均值向量为μ=(μ1,μ2,… …,μm,)`,协方差阵为∑=(σij),
则样本X=(X1,X2,… …,Xm,)`与总体G的马氏距离定义为:
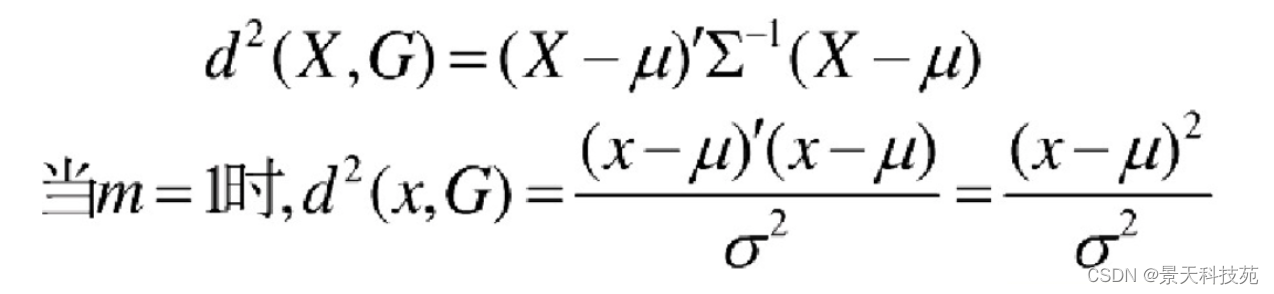
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为∑的随机变量的差异程度:如果协方差矩阵为单位矩阵,马氏距离就简化为欧式距离;如果协方差矩阵为对角矩阵,则其也可称为正规化的欧式距离。
马氏距离特性:
1.量纲无关,排除变量之间的相关性的干扰;
2.马氏距离的计算是建立在总体样本的基础上的,如果拿同样的两个样本,放入两个不同的总体中,最后计算得出的两个样本间的马氏距离通常是不相同的,除非这两个总体的协方差矩阵碰巧相同;
3 .计算马氏距离过程中,要求总体样本数大于样本的维数,否则得到的总体样本协方差矩阵逆矩阵不存在,这种情况下,用欧式距离计算即可。
4.还有一种情况,满足了条件总体样本数大于样本的维数,但是协方差矩阵的逆矩阵仍然不存在,比如三个样本点(3,4),(5,6),(7,8),这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下,也采用欧式距离计算。
欧式距离&马氏距离:
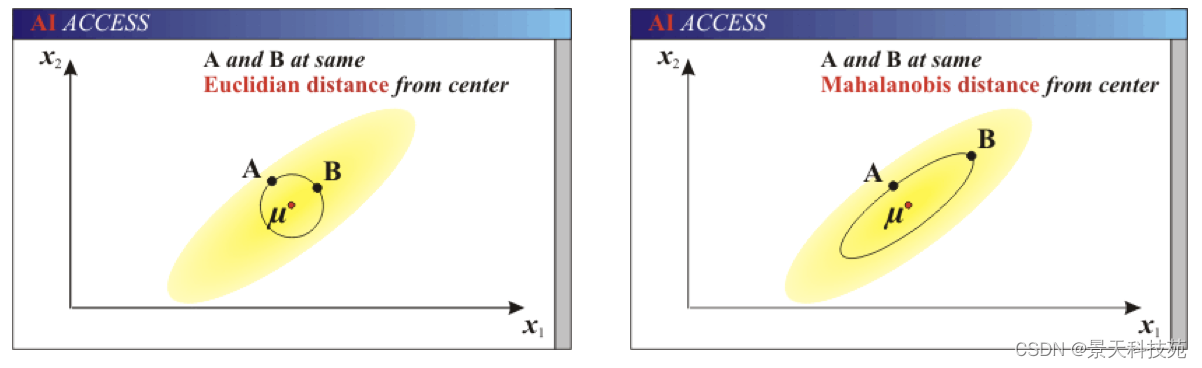
举例:
已知有两个类G1和G2,比如G1是设备A生产的产品,G2是设备B生产的同类产品。设备A的产品质量高(如考察指标为耐磨度X),其平均耐磨度μ1=80,反映设备精度的方差σ2(1)=0.25;设备B的产品质量稍差,其平均耐磨损度μ2=75,反映设备精度的方差σ2(2)=4.
今有一产品G0,测的耐磨损度X0=78,试判断该产品是哪一台设备生产的?
直观地看,X0与μ1(设备A)的绝对距离近些,按距离最近的原则,是否应把该产品判断设备A生产的?
考虑一种相对于分散性的距离,记X0与G1,G2的相对距离为d1,d2,则:
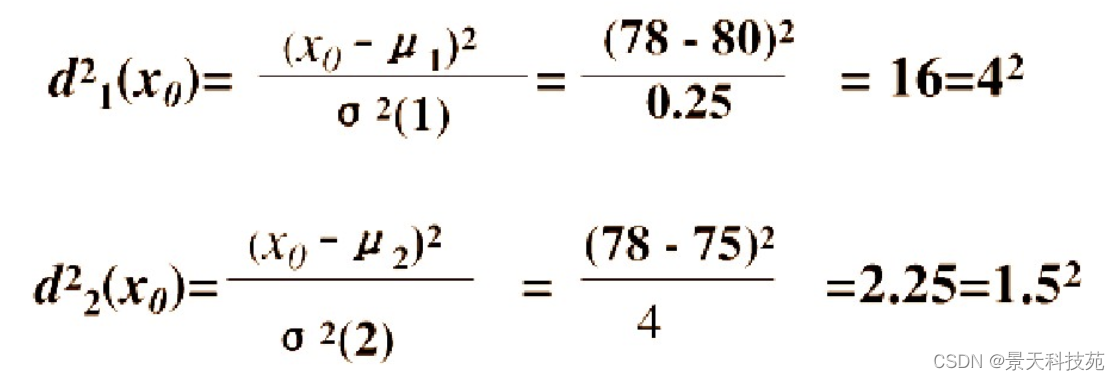
因为d2=1.5 < d1=4,按这种距离准则,应判断X0为设备B生产的。
设备B生产的产品质量较分散,出现X0为78的可能性较大;而设备A生产的产品质量较集中,出现X0为78的可能性较小。
这种相对于分散性的距离判断就是马氏距离。
10 “连续属性”和“离散属性”的距离计算
我们常将属性划分为“连续属性(continuous attribute)和"离散属性(categorical attribute),前者在定义域上有无穷多个可能的取值,后者在定义域上是有限个取值
若属性值之间存在序关系,则可以将其转化为连续值,例如: 身高属性“高”“中等”“矮”,可转化为(1,0.5,0}。
闵可夫斯基距离可以用于有序属性。
若属性值之间不存在序关系,则通常将其转化为向量的形式,例如:性别属性“男”“女””,可转化为{ (1,0) ,(0,1) }。
相关文章:

机器学习--K-近邻算法常见的几种距离算法详解
文章目录 距离度量1 欧式距离(Euclidean Distance)2 曼哈顿距离(Manhattan Distance)3 切比雪夫距离 (Chebyshev Distance)4 闵可夫斯基距离(Minkowski Distance)5 标准化欧氏距离 (Standardized EuclideanDistance)6 余弦距离(Cosine Distance)7 汉明距离(Hamming Distance)【…...
常用术语整理》)
<网络安全>《30 网络信息安全基础(1)常用术语整理》
1 肉鸡 所谓“肉鸡”是一种很形象的比喻,比喻那些可以随意被我们控制的电脑,对方可以是WINDOWS系统,也可以是UNIX/LINUX系统,可以是普通的个人电脑,也可以是大型的服务器,我们可以象操作自己的电脑那样来操…...
Git远程仓库的使用(Gitee)及相关指令
目录 1 远程仓库的创建和配置 1.1 创建远程仓库 1.2 设置SSH公钥 2 指令 2.1 git remote add 远端名称(一般为origin) 仓库路径 2.2 git remote 2.3 git push [-f] [--set-upstream] [远端名称 [本地分支名][:远端分支名]] 2.3 git clone url 2.4 git fetch 2.5 git p…...
vscode +markdown 的安装和使用
文章目录 前言一、vscode markdown 是什么?1.vscode是什么?2.markdown 是什么? 二、安装步骤1.下载2.安装 三、安装插件1.安装 Markdown All in One2.安装 Markdown Preview Enhanced3. Paste Image v1.0.44.LimfxCodeExv0.7.105.Code Spell …...
Python爬虫之自动化测试Selenium#7
爬虫专栏:http://t.csdnimg.cn/WfCSx 前言 在前一章中,我们了解了 Ajax 的分析和抓取方式,这其实也是 JavaScript 动态渲染的页面的一种情形,通过直接分析 Ajax,我们仍然可以借助 requests 或 urllib 来实现数据爬取…...

快速学习Spring
Spring 简介 Spring 是一个开源的轻量级、非侵入式的 JavaEE 框架,它为企业级 Java 应用提供了全面的基础设施支持。Spring 的设计目标是简化企业应用的开发,并解决 Java 开发中常见的复杂性和低效率问题。 Spring常用依赖 <dependencies><!-…...

c语言操作符(上)
目录 编辑 原码、反码、补码 1、正数 2、负数 3、二进制计算1-1 移位操作符 1、<<左移操作符 2、>>右移操作符 位操作符&、|、^、~ 1、&按位与 2、|按位或 3、^按位异或 特点 4、~按位取反 原码、反码、补码 1、正数 原码 反码 补码相同…...

vue3 可视化大屏自适应屏幕组件
首先定义了一个名叫ScreenContainerOptions的组件,需要传的参数如下 export type ScreenContainerOptions {width?: string | numberheight?: string | numberscreenFit?: boolean // 是否开启屏幕自适应,不然会按比例显示 } 组件的主要代码如下 …...

SpringCloud入门概述
1. 介绍 Spring Cloud 1.1 什么是 Spring Cloud Spring Cloud 是一个基于 Spring Boot 的微服务架构开发工具集,它为开发者提供了一系列开箱即用的工具和库,用于构建分布式系统中的微服务架构。Spring Cloud 提供了诸如服务发现、配置中心、负载均衡、…...

刷题计划_冲绿名
现在 rating 是 1104 准备刷 100道 1200的题,把实力提升到 1200 ,上一个绿名 每一个分数段的题都写一百道,争取早日上蓝 现在 虽然 cf 里面显示写了一些这个分数段的题,但是自己训练的时候,其实是没有训练一道这个分…...

【微信小程序开发】小程序版的防抖节流应该怎么写
由于微信小程序与普通网页的开发、编译、运行机制都有所不同,在防抖节流的方法使用上也就需要我们做一些比较棘手的适配操作。常见的H5开发的防抖节流此处就不再分享了,网上有太多的教程,或者直接问那群AI即可。 OK,言归正传&…...

单片机学习笔记---蜂鸣器播放提示音音乐(天空之城)
目录 蜂鸣器播放提示音 蜂鸣器播放音乐(天空之城) 准备工作 主程序 中断函数 上一节讲了蜂鸣器驱动原理和乐理基础知识,这一节开始代码演示! 蜂鸣器播放提示音 先创建工程:蜂鸣器播放提示音 把我们之前模块化的…...
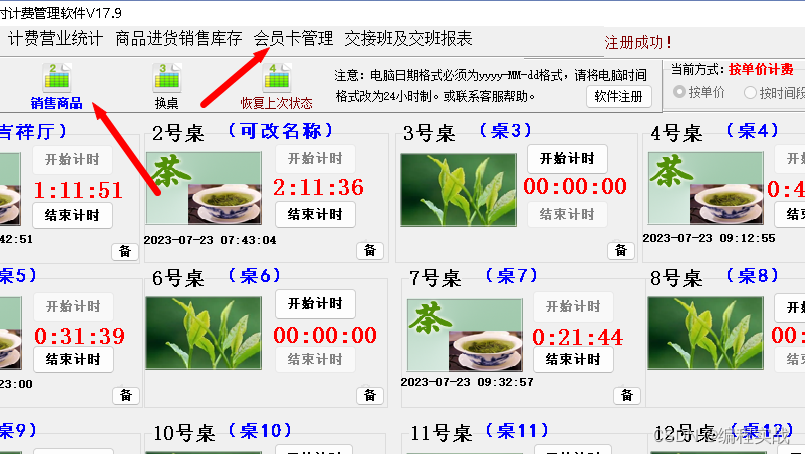
软件实例分享,茶楼收银软件管理系统,支持计时计费商品销售会员管理定时语音提醒功能
软件实例分享,茶楼收银软件管理系统,支持计时计费商品销售会员管理定时语音提醒功能 一、前言 以下软件教程以 佳易王茶社计时计费管理系统软件V18.0为例说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 问:这个软…...
clang前端
Clang可以处理C、C和Objective-C源代码 Clang简介 Clang可能指三种不同的实体: 前端(在Clang库中实现)编译驱动程序(在clang命令和Clang驱动程序库中实现)实际的编译器(在clang-ccl命令中实现࿰…...
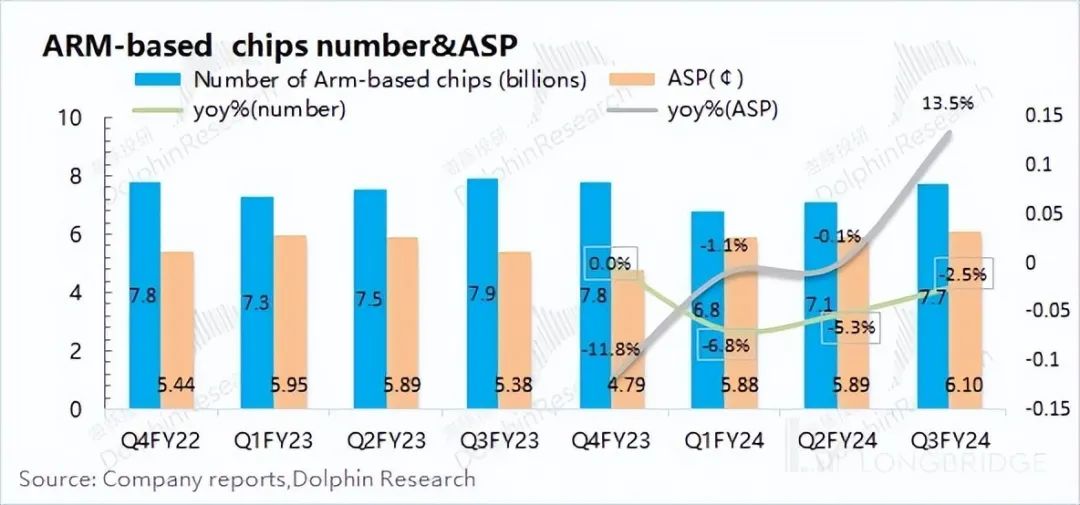
ARM:AI 的翅膀,还能飞多久?
ARM(ARM.O)于北京时间 2024 年 2 月 8 日上午的美股盘后发布了 2024 年第三财年报告(截止 2023 年 12 月),要点如下: 1、整体业绩:收入再创新高。ARM 在 2024 财年第三季度(即 23Q4…...
【C语言】常见字符串函数的功能与模拟实现
目录 1.strlen() 模拟实现strlen() 2.strcpy() 模拟实现strcpy() 3.strcat() 模拟实现strcat() 4.strcmp() 模拟实现strcmp() 5.strncpy() 模拟实现strncpy() 6.strncat() 模拟实现strncat() 7.strncmp() 模拟实现strncmp() 8.strstr() 模拟实现strstr() 9.str…...

pyGMT初步使用
文章目录 安装显示地图保存地图 安装 GMT,即Generic Mapping Tools,通用制图工具,是GIS领域应用最广泛的制图软件之一,用于绘制地图、图形以及进行地球科学数据分析和可视化。而pyGMT即其为python提供的函数接口,故而…...
神经网络 | CNN 与 RNN——深度学习主力军
Hi,大家好,我是半亩花海。本文主要将卷积神经网络(CNN)和循环神经网络(RNN)这两个深度学习主力军进行对比。我们知道,从应用方面上来看,CNN 用于图像识别较多,而 RNN 用于…...
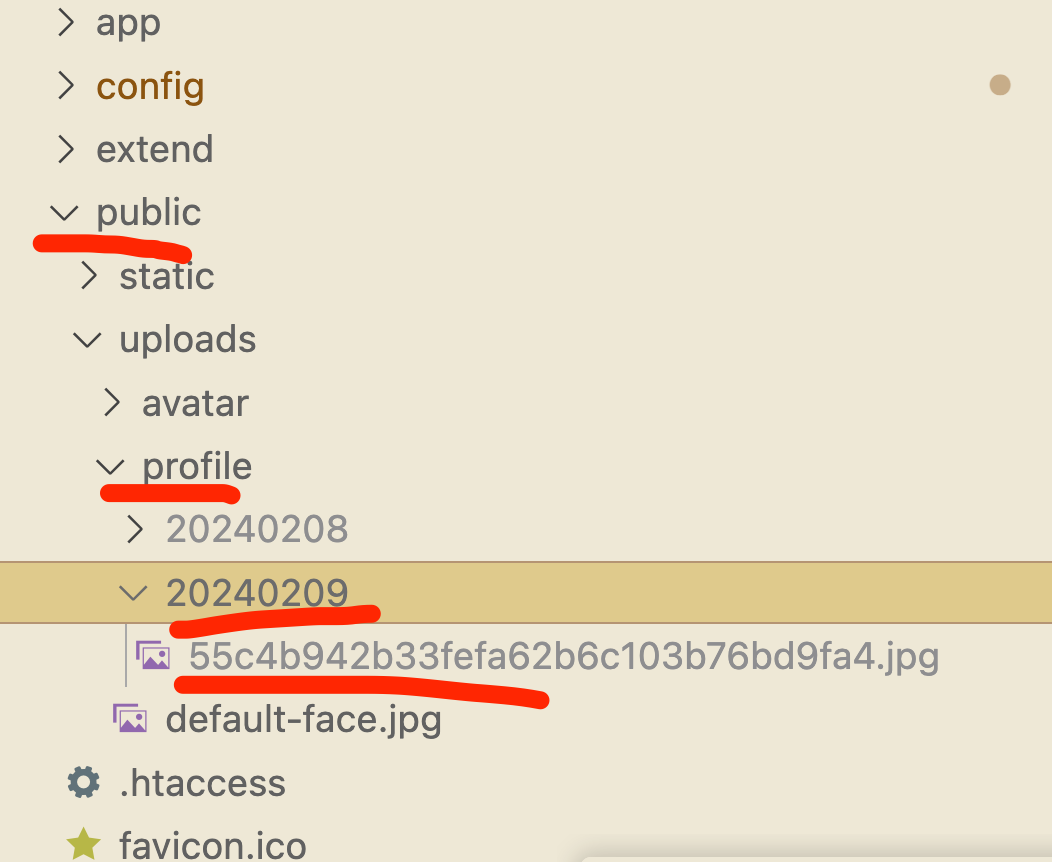
thinkphp6入门(20)-- 如何上传图片、文件
1. 配置文件 设置上传的路径 对应文件夹 2. 前端 <div class"card-body"><h1 class"card-title">用户头像</h1><img src"../../../uploads/{$user.avatar_photo_path}" alt"avatar" height"100"/&g…...
【Linux技术宝典】深入理解Linux基本指令:命令行新手指南
📷 江池俊: 个人主页 🔥个人专栏: ✅数据结构冒险记 ✅Linux技术宝典 🌅 有航道的人,再渺小也不会迷途。 文章目录 一、Linux下基本指令1. ls 指令2. pwd指令3. clear指令4. cd指令什么是家目录…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
