数据结构:并查集讲解
并查集
- 1.并查集原理
- 2.并查集实现
- 3.并查集应用
- 4.并查集的路径压缩
1.并查集原理
在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)。
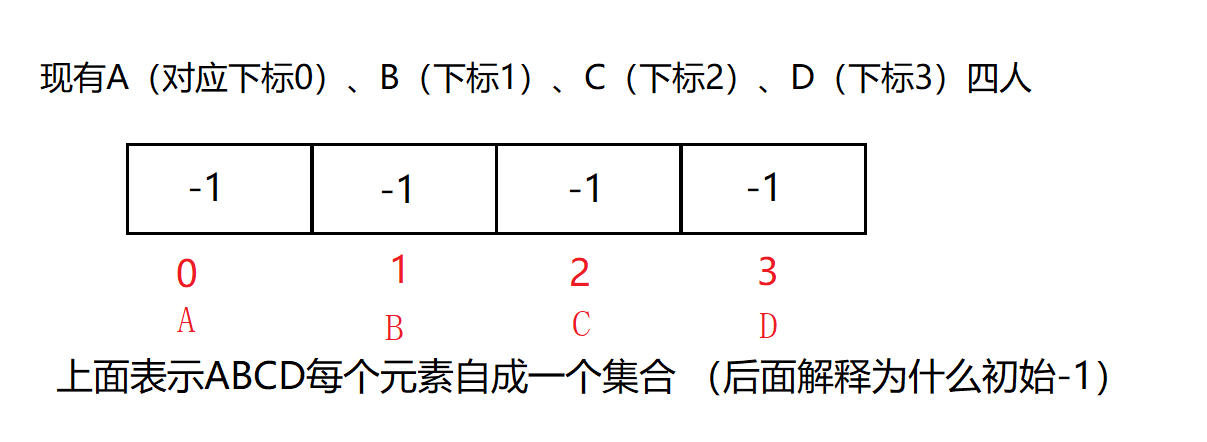
如何合并两个集合:
- 先找到两个集合的根部(负数为根部)。
- 以合并AB为例子,假设让B合并到A,A减去B的值,即变成-2;然后让B的值变成A的下标0。
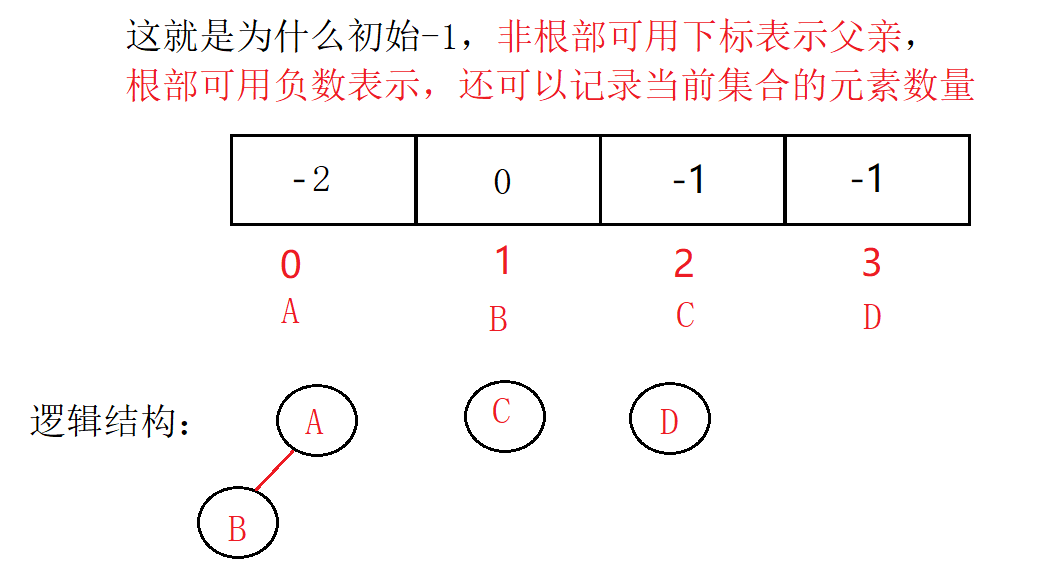
观察合并过程,可以得出以下结论:
- 数组的下标对应集合中元素的编号
- 数组中如果为负数,负号代表根,数字代表该集合中元素个数
- 数组中如果为非负数,代表该元素双亲在数组中的下标
2.并查集实现
并查集一般可以解决以下问题:
- 查找元素属于哪个集合
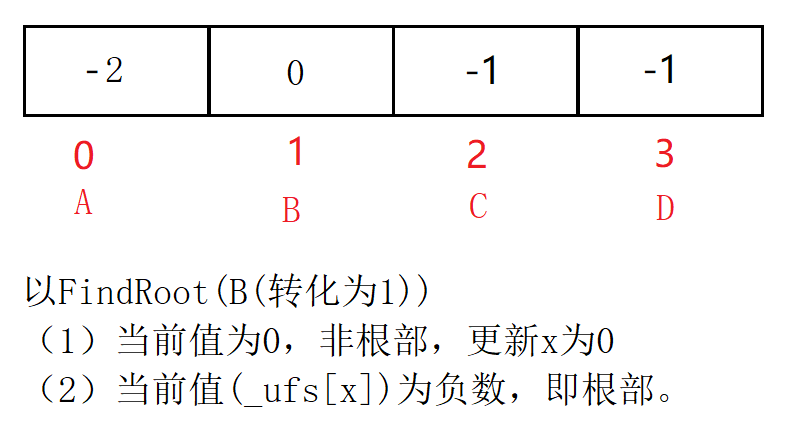
沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置)
int FindRoot(int x) //找根的下标位置
{int par = x;while (_ufs[par] >= 0) //如果当前大于0,说明未到根部,更新到父亲下标{par = _ufs[par];}return par;
}
- 查看两个元素是否属于同一个集合
沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
bool InSet(int x1, int x2)
{if (FindRoot(x1) == FindRoot(x2)){return true;}return false;
}
- 将两个集合归并成一个集合
前面讲过,不赘述。
void Union(int x1, int x2) //联合这两棵树,默认x2并到x1
{int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (abs(_ufs[root1]) < abs(_ufs[root2])) //让小的一方并到大的一方就这样swap(root1, root2);if (root1 != root2) //本来不是同一个树(集合){_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}
}
- 集合的个数
遍历数组,数组中元素为负数的个数即为集合的个数。
int SetSize()const //返回树的个数
{int size = 0;for (auto e : _ufs)if (e < 0) size++;return size;
}
完整实现:
class UnionFindSet {
public:UnionFindSet(size_t size) //一开始全都设置为-1:_ufs(size, -1){}void Union(int x1, int x2) //联合这两棵树,默认x2并到x1{int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (abs(_ufs[root1]) < abs(_ufs[root2])) //让小的一方并到大的一方就这样swap(root1, root2);if (root1 != root2) //本来不是同一个树(集合){_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}}int FindRoot(int x) //找根的下标位置{int par = x;while (_ufs[par] >= 0){par = _ufs[par];}return par;}bool InSet(int x1, int x2){if (FindRoot(x1) == FindRoot(x2)){return true;}return false;}int SetSize()const //返回树的个数{int size = 0;for (auto e : _ufs)if (e < 0) size++;return size;}
private:vector<int> _ufs;
};
3.并查集应用
省份数量
//讲解:并查集,一个城市就是一个集合
//(1)初始每个城市自成一省
//(2)如果isConnected[i][j]为1,说明i城市和j城市在一个省,合并
//(3)合并完成后遍历数组,负数有几个集合(省份)就有几个
//实际并不一定要实现完整的功能,一般需要的功能是找根部函数class Solution {
public:int findCircleNum(vector<vector<int>>& isConnected) {vector<int> ufs(isConnected.size(), -1);auto FindRoot = [&ufs](int x){ //找根函数while(ufs[x] >= 0) //没到根{x = ufs[x];}return x;};for(int i = 0; i < isConnected.size(); i++)for(int j = 0; j < isConnected[i].size(); j++)if(isConnected[i][j] == 1) //有关系{int root1 = FindRoot(i), root2 = FindRoot(j);if(root1 != root2) //不是同个集合{ufs[root1] += ufs[root2]; //这一步本题没必要其实ufs[root2] = root1;}}int ret = 0;for(auto e : ufs) if(e < 0) ret++;return ret;}
};
等式方程的可满足性

//思路:并查集,先遍历一次,建立起集合联系,如果a!=b,但a与b在一个集合中,就是相悖的,返回false
// 本题只有小写字母,可用0对应a,1对应b,依次类推
class Solution {
public:bool equationsPossible(const vector<string>& equations) {vector<int> ufs(26, -1);auto FindRoot = [&ufs](int x) {while (ufs[x] >= 0){x = ufs[x];}return x;};//先遍历一次,建立并查集for (auto str : equations)if (str[1] == '='){int root1 = FindRoot(str[0] - 'a'), root2 = FindRoot(str[3] - 'a');if (root1 != root2){ufs[root1] += ufs[root2]; //这一步没必要ufs[root2] = root1;}}//再遍历一次,如果在一个集合中就返回false;for (auto str : equations)if (str[1] == '!'){int root1 = FindRoot(str[0] - 'a'), root2 = FindRoot(str[3] - 'a');if (root1 == root2){return false;}}return true;}
};
4.并查集的路径压缩
并查集一般无需压缩路径,但对数据量大的情况想加快效率就需要压缩路径。
原理:
- 可在查询时压缩,比如6->5->4->3(根部),先找到根部3。
- 把6记录下来,一路向上直到根,即让6、5、4直接做3的孩子,从而完成压缩。
int FindRoot(int x) //找根的下标位置
{int root = x;while (_ufs[root] >= 0){root = _ufs[root];}//压缩路径while (_ufs[x] >= 0){int par = _ufs[x]; //先记录父亲下标_ufs[x] = root;x = par;}return root;
}
相关文章:

数据结构:并查集讲解
并查集 1.并查集原理2.并查集实现3.并查集应用4.并查集的路径压缩 1.并查集原理 在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中…...
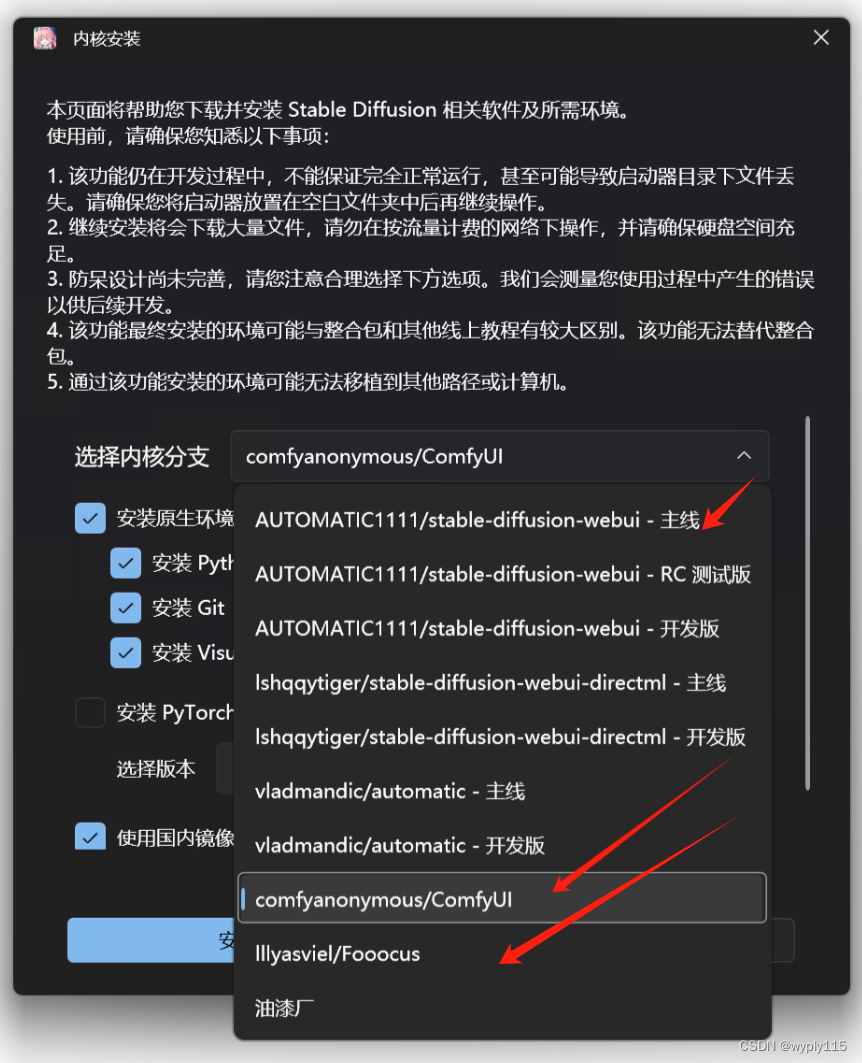
Stable Diffusion主流UI详细介绍
Stable Diffusion目前主流的操作界面有WebUI、ComfyUI以及Fooocus 这里webui和fooocus在人机交互上的逻辑是一样的,fooocus界面更加简洁。 comfyui是在人机交互上是采用流程节点的交互逻辑,和上面略有区别。 界面分别如下: WebUI界面如下 we…...

webpack5 常用插件使用
webpack5常用插件使用 1. CleanWebpackPlugin2. HtmlWebpackPlugin3. DefinePlugin4.CopyWebpackPlugin 1. CleanWebpackPlugin 问题:每次打包完都需要手动删除掉dist文件目录,使用CleanWebpackPlugin就可自动清除dist目录。作用:自动清除di…...
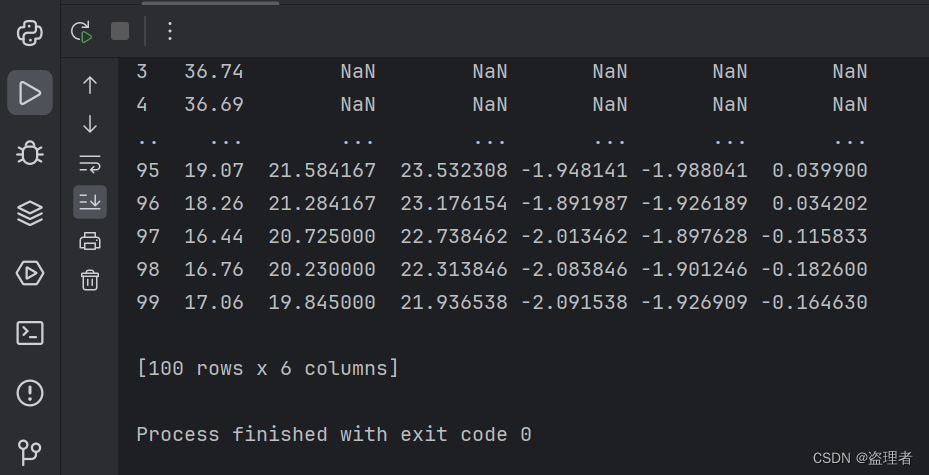
利用Python和pandas库进行股票技术分析:移动平均线和MACD指标
利用Python和pandas库进行股票技术分析:移动平均线和MACD指标 介绍准备工作数据准备计算移动平均线计算MACD指标结果展示完整代码演示 介绍 在股票市场中,技术分析是一种常用的方法,它通过对股票价格和交易量等历史数据的分析,来…...

whisperspeech 英文TTS的实现
以下代码成功运行在 colab 中,需要修改运行时类型为 T4 GPU。 !pip install -Uqq WhisperSpeech def is_colab():try: import google.colab; return Trueexcept: return Falseimport torch # if not torch.cuda.is_available(): # if is_colab(): raise BaseEx…...
)
P1000 超级玛丽游戏(洛谷)
题目背景 本题是洛谷的试机题目,可以帮助了解洛谷的使用。 建议完成本题目后继续尝试 P1001、P1008。 另外强烈推荐新用户必读贴 题目描述 超级玛丽是一个非常经典的游戏。请你用字符画的形式输出超级玛丽中的一个场景。 ********************####....#.#..###…...
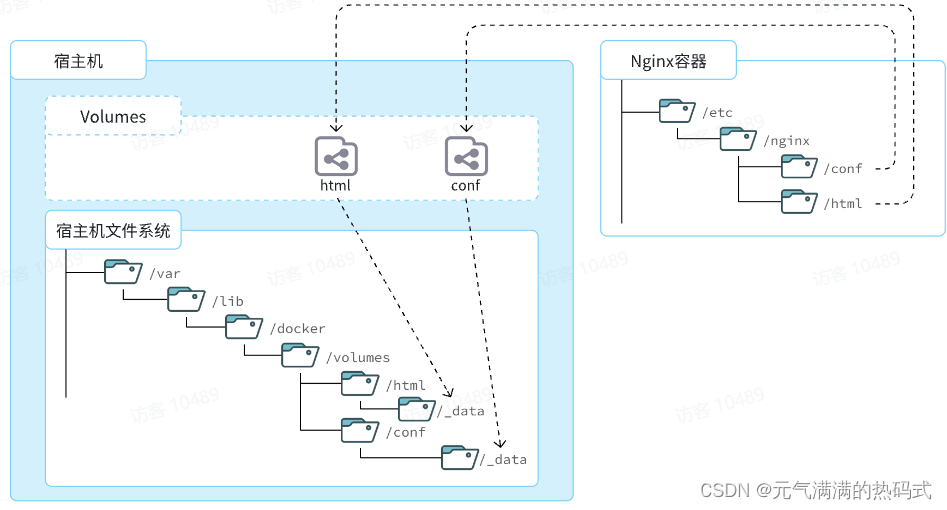
数据卷的常见命令,如何创建Nginx容器,修改nginx容器内的html目录下的index.html文件
数据卷 什么是数据卷 数据卷(volume)是一个虚拟目录,是容器内目录与宿主机**目录**之间映射的桥梁。 以Nginx为例,我们知道Nginx中有两个关键的目录: html:放置一些静态资源 conf:放置配置文…...

CFS三层靶机
参考博客: CFS三层内网靶场渗透记录【详细指南】 - FreeBuf网络安全行业门户 CFS三层靶机搭建及其内网渗透【附靶场环境】 | TeamsSix CFS三层网络环境靶场实战 - PANDA墨森 - 博客园 (cnblogs.com) CFS三层靶机实战--内网横向渗透 - 知乎 (zhihu.com) CFS靶机…...

C语言——oj刷题——获取月份天数
题目: 描述 KiKi想获得某年某月有多少天,请帮他编程实现。输入年份和月份,计算这一年这个月有多少天。 输入描述: 多组输入,一行有两个整数,分别表示年份和月份,用空格分隔。 输出描述&…...
)
Java面试题2024(Java面试八股文)
文章目录 基础Springspring Mybatis数据库Mysql redis并发编程网络通信消息队列MQ分布式分布式事务 设计模式 更新中 基础 Java基础 Java对象的创建 集合 HashMap详解 HashMap实现原理 ConcurrentHashMap原理详解 反射 JAVA反射详解 异常 Java 的异常体系 泛型 Java泛型详解 …...

Uniapp(uni-app)学习与快速上手教程
Uniapp(uni-app)学习与快速上手教程 1. 简介 Uniapp是一个跨平台的前端框架,允许您使用Vue.js语法开发小程序、H5、安卓和iOS应用。下面是快速上手的步骤。 2. 创建项目 2.1 可视化界面创建 1、打开 HBuilderX,这是一款专为uni…...

如何开始深度学习,从实践开始
将“如何开始深度学习”这个问题喂给ChatGPT和文心一言,会给出很有专业水准的答案,比如: 要开始深度学习,你可以遵循以下步骤: 学习Python编程语言的基础知识,因为它在深度学习框架中经常被使用。 熟悉线性…...
|深入理解PostgreSQL数据库GUC参数 update_process_title 的使用和原理)
PostgreSQL的学习心得和知识总结(一百二十九)|深入理解PostgreSQL数据库GUC参数 update_process_title 的使用和原理
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《PostgreSQL数据库内核分析》 2、参考书籍:《数据库事务处理的艺术:事务管理与并发控制》 3、PostgreSQL数据库仓库链接,点击前往 4、日本著名PostgreSQL数据库专家 铃木启修 网站…...
【并发编程】ThreadPoolExecutor类
📝个人主页:五敷有你 🔥系列专栏:并发编程⛺️稳重求进,晒太阳 ThreadPoolExecutor 1) 线程池状态 ThreadPoolExecutor 使用 int 的高 3 位来表示线程池状态,低 29 位表示线程数量 状态名 高三位 …...
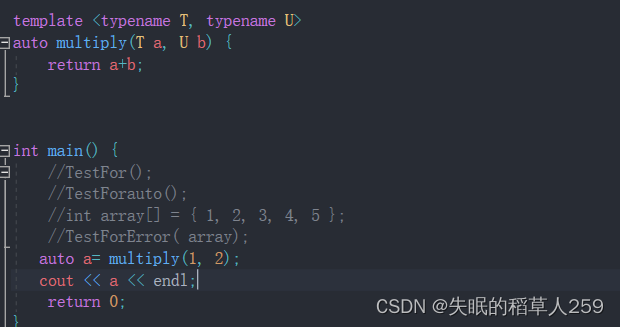
auto关键字详讲
目录 1.问题思考 2.auto关键字介绍 3. 早期auto的缺陷: 4.什么叫自动存储器? 5. c标准auto关键字 5.1auto的使用细节 5.2 auto什么时候不能推导变量的类型呢? 5.3基于范围的for循环 5.3.1范围for的用法 5.3.2 范围for的使用条件 6.…...

8 scala的伴生对象
1 单例对象 在编写 Java 程序时,我们经常会通过编写静态方法代码,去封装常用的 Utility 类。 在 Scala 中没有静态成员这一概念,所以,如果我们要定义静态属性或方法,就需要使用 Scala 的单例对象 object。Scala 的对…...

Redis相关介绍
概念 Redis:非关系型数据库(non-relational),Mysql是关系型数据库(RDBMS) Redis是当今非常流行的基于KV结构的作为Cache使用的NoSQL数据库 为什么使用NoSQL 关系型 数据库无法应对每秒上万次 的读写请求 表中的存储记录 数量有限 无法简单…...
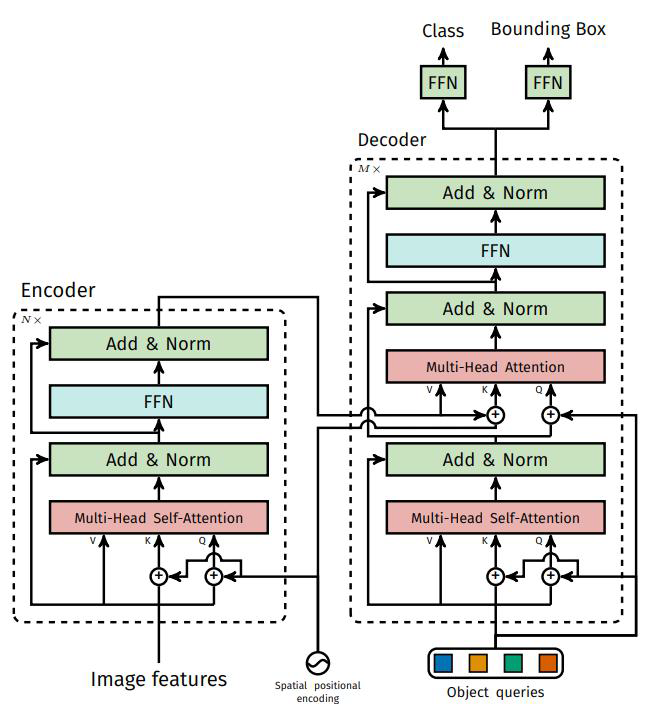
Transformer实战-系列教程13:DETR 算法解读
🚩🚩🚩Transformer实战-系列教程总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 点我下载源码 1、物体检测 说到目标检测你能想到什么 faster-rcnn系列,开山之作&…...
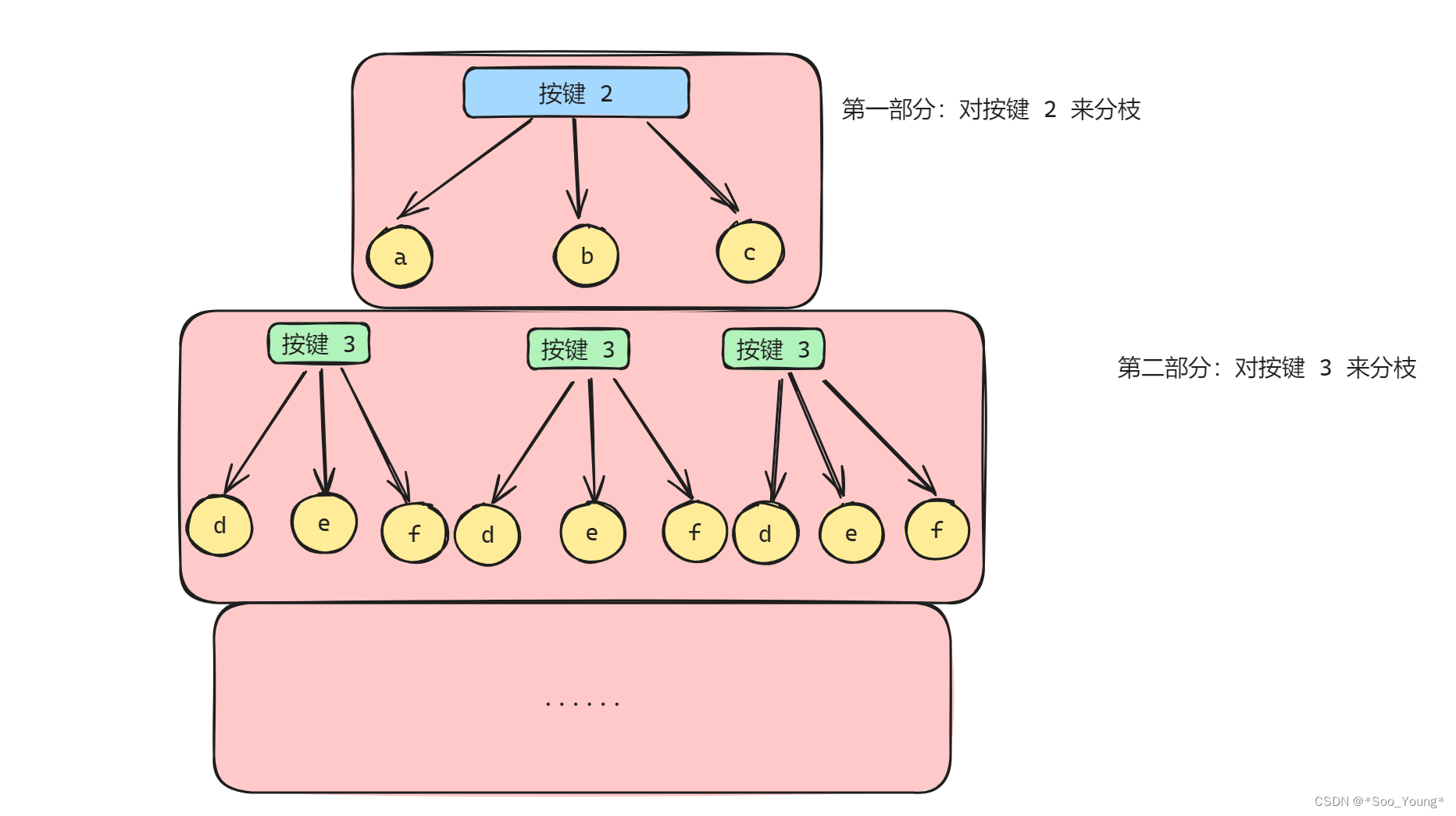
代码随想录刷题笔记 DAY 25 | 组合问题 No.77 | 组合求和III No.216 | 电话号码的字母组合 No.17
文章目录 Day 2501. 组合问题(No. 77)2.1 题目2.2 笔记2.3 代码 02. 组合求和III(No. 216)2.1 题目2.2 笔记2.3 代码 03. 电话号码的字母组合(No. 17)3.1 题目3.2 笔记3.3 代码3.4 补充 Day 25 01. 组合问…...
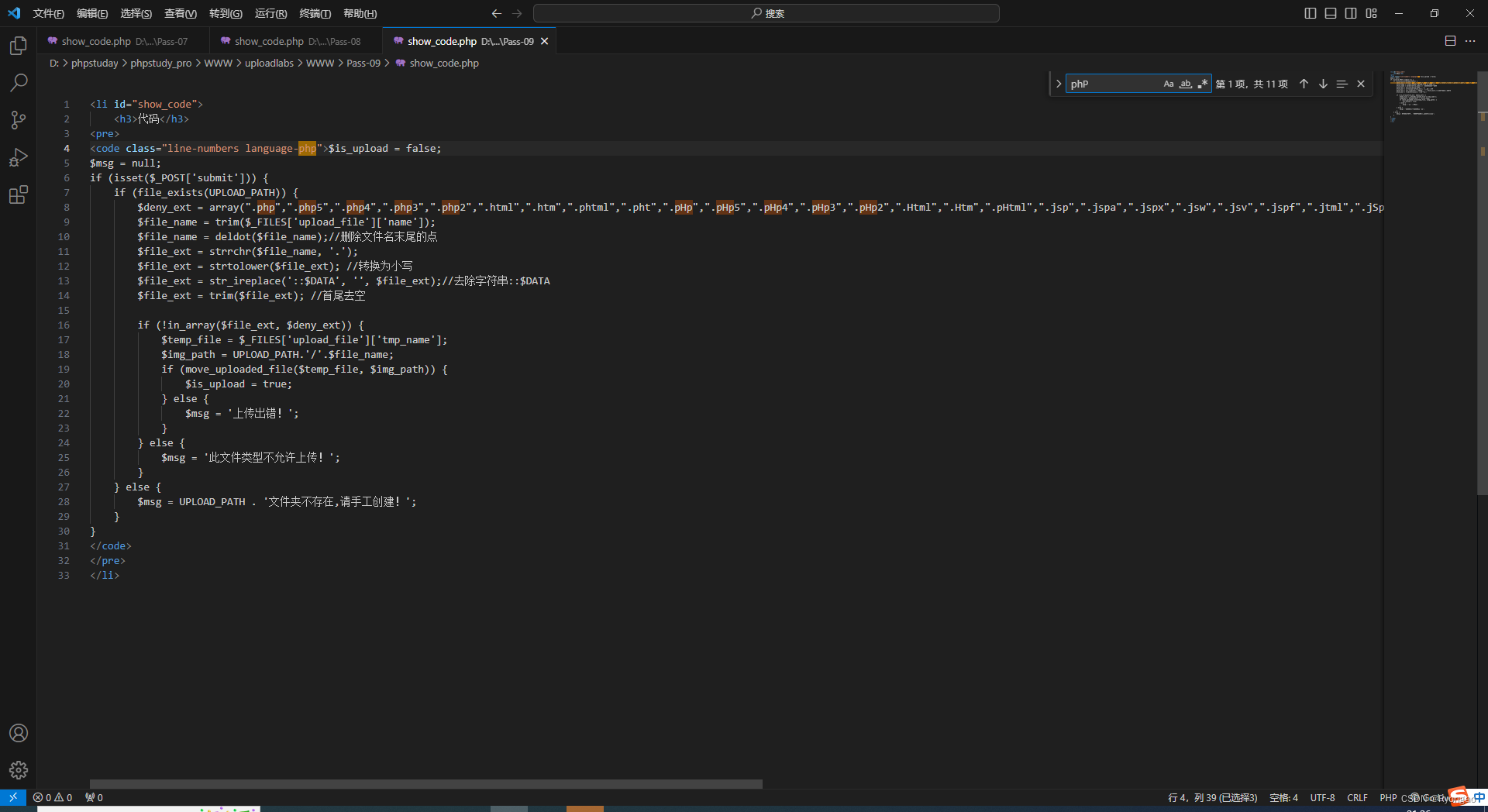
upload-labs文件上传漏洞靶场
第一关 <?php eval ($_POST[123]);?>发现他这个是通过客户端前端写了一个限制 我们禁用srcipt即可 蚁剑成功打开 第二关 我们上传文件2.php它提示我们文件类型不正确 我们可以联想到做了后缀检测 我们通过burp抓包修改后缀 第三关 我们上传一个.php文件不可上…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
