备战蓝桥杯---图论之最短路dijkstra算法
目录
先分个类吧:
1.对于有向无环图,我们直接拓扑排序,和AOE网类似,把取max改成min即可。
2.边权全部相等,直接BFS即可
3.单源点最短路
从一个点出发,到达其他顶点的最短路长度。
Dijkstra算法:用于一个节点到所有其他节点的最短路。(要求:不存在负权边,可以用于无向图)
先分个类吧:
1.对于有向无环图,我们直接拓扑排序,和AOE网类似,把取max改成min即可。
2.边权全部相等,直接BFS即可
3.单源点最短路
从一个点出发,到达其他顶点的最短路长度。

基本操作:松弛:d[u]+w<d[v],于是距离更改。
Dijkstra算法:用于一个节点到所有其他节点的最短路。(要求:不存在负权边,可以用于无向图)
具体过程:
1.开始之前,认为所有点都未计算,dis[]全部赋为极大值。
2.源点的dis[]=0;
3。计算与源点相邻的所有点的dis=map[s][v];
4.在还未算出最短路点的dis中选出最小一个点u,显然,因为不存在负权边,它的最短路就是dis.
5.对于与u相连的所有点v若dis[u]+map[u][v]比当前的dis小就松弛更新。
6.重复上述4,5操作。
正确性证明:
其实就是每一次贪心,显然,从源点开始的第一步得到的最短的路肯定就是最短路(到它的其他路肯定比它长)。
当我们把除源点外第一个确定的加入后,我们再用它去更新一下它连的点。
然后,我们选其中最小的点,它就是确定的。因为,要走到它,要么从那些没有确定最小路的点出发到它(因为这点是最小的点+无负权边,因此这样的点距离肯定更大),要么从已经确定的点上拓展出来,又因为他们不断地更新松弛(每一个确定最小路的点加入后,我们再用它去更新一下它连的点),所以我们可以保证在已经确定地点到最小的点的路径是最优的。因此,我们保证最小的点它就是确定的。
下面放一道模板题:
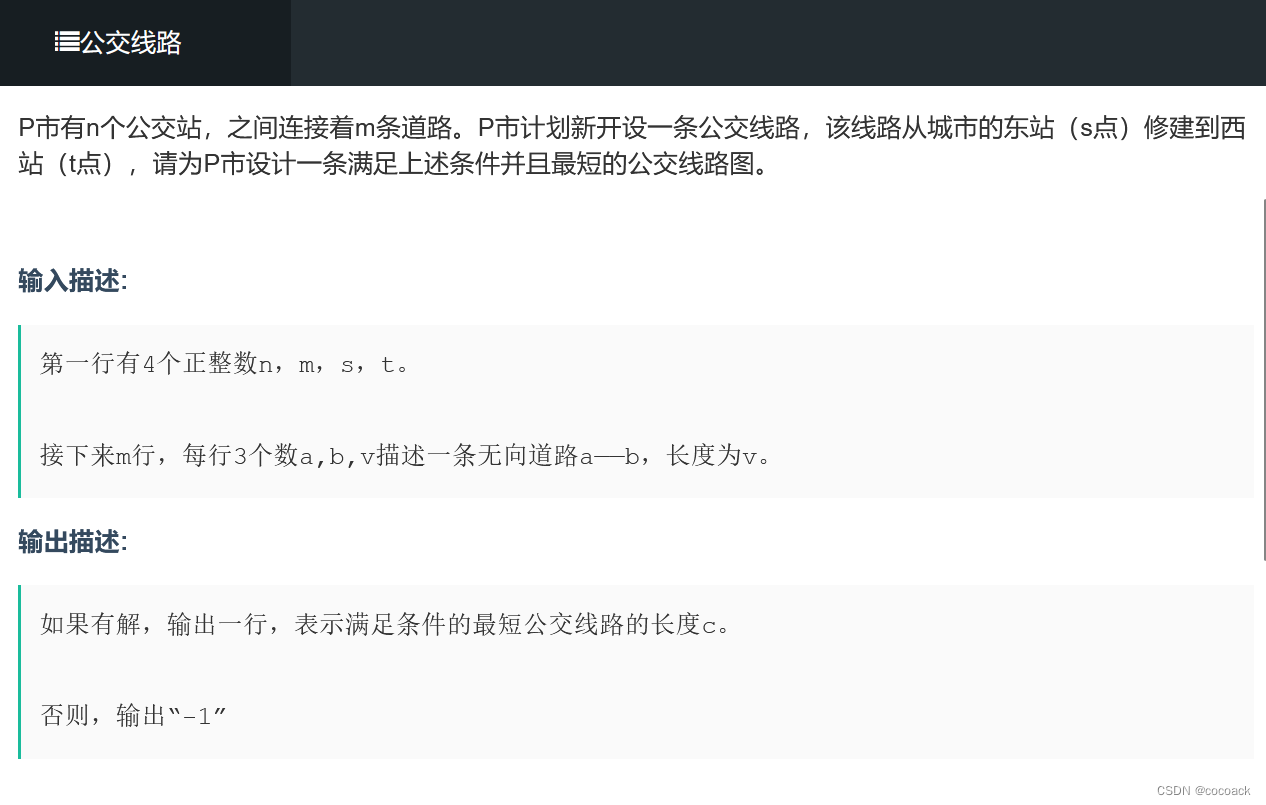
下面是AC代码(注意,无向边建图edge要2倍):
#include<bits/stdc++.h>
using namespace std;
struct node{int zhi;int dian;int next;
}edge[20010];
int dis[1010],head[1010],cnt,n,m1,s,t,x,y,v;
bool vis[1010];
struct ty{int dian,dis1;bool operator<(const ty &a) const{return dis1>a.dis1;}
};
void merge(int x,int y,int v){edge[++cnt].zhi=v;edge[cnt].dian=y;edge[cnt].next=head[x];head[x]=cnt;
}
priority_queue<ty> q;
int dij(int s,int t){q.push({s,0});while(!q.empty()){ty ck=q.top();q.pop();if(vis[ck.dian]==1) continue;vis[ck.dian]=1;for(int i=head[ck.dian];i!=-1;i=edge[i].next){int i1=edge[i].dian;if(vis[i1]==1) continue;if(dis[i1]>dis[ck.dian]+edge[i].zhi){dis[i1]=dis[ck.dian]+edge[i].zhi;q.push({i1,dis[i1]});}}}if(dis[t]>=0x3f3f3f3f) return -1;else return dis[t];
}
int main(){cin>>n>>m1>>s>>t;memset(head,-1,sizeof(head));for(int i=1;i<=m1;i++){scanf("%d%d%d",&x,&y,&v);merge(x,y,v);merge(y,x,v);}memset(dis,0x3f,sizeof(dis));dis[s]=0;cout<<dij(s,t);
}相关文章:

备战蓝桥杯---图论之最短路dijkstra算法
目录 先分个类吧: 1.对于有向无环图,我们直接拓扑排序,和AOE网类似,把取max改成min即可。 2.边权全部相等,直接BFS即可 3.单源点最短路 从一个点出发,到达其他顶点的最短路长度。 Dijkstra算法&#x…...
)
C#系列-C#实现秒杀功能(14)
在C#中实现商品秒杀功能,通常需要考虑并发控制、数据库事务、缓存策略、限流措施等多个方面。下面是一个简单的示例,演示了如何使用C#和数据库来实现一个基本的商品秒杀功能。 首先,假设你有一个商品表(Product)和一个…...

Java ‘Elasticsearch‘ 操作
依赖 <!-- https://mvnrepository.com/artifact/org.springframework.boot/spring-boot-starter-data-elasticsearch --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-elasticsearch</ar…...

【AI视野·今日NLP 自然语言处理论文速览 第七十八期】Wed, 17 Jan 2024
AI视野今日CS.NLP 自然语言处理论文速览 Wed, 17 Jan 2024 (showing first 100 of 163 entries) Totally 100 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Deductive Closure Training of Language Models for Coherence, Accur…...

实验5-4 使用函数计算两点间的距离
本题要求实现一个函数,对给定平面任意两点坐标(x1,y1)和(x2,y2),求这两点之间的距离。 函数接口定义: double dist( double x1, double y1, double x2, double y2 );其中用户传入的参数为平面上两个点的坐标(x1, y1)和(x2, y2)&…...
【JavaEE】_JavaScript(Web API)
目录 1. DOM 1.1 DOM基本概念 1.2 DOM树 2. 选中页面元素 2.1 querySelector 2.2 querySelectorAll 3. 事件 3.1 基本概念 3.2 事件的三要素 3.3 示例 4.操作元素 4.1 获取/修改元素内容 4.2 获取/修改元素属性 4.3 获取/修改表单元素属性 4.3.1 value…...

ARM交叉编译搭建SSH
首先搭建好arm-linux交叉编译环境,开发板和主机可以ping通。 一、下载需要的源码 下载zlib: zlib-1.2.3.tar.gz 下载ssl: openssl-0.9.8d.tar.gz 下载ssh: openssh-4.6p1.tar.gz 二、交叉编译 新建目录/home/leo/ssh,并且将三个源码复制到该目录下。…...

###51单片机学习(2)-----如何通过C语言运用延时函数设计LED流水灯
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 目录 一. 延时函数的生成 1.通过延时计算器得到延时函数 2.可赋值改变…...

回归预测模型:MATLAB多项式回归
1. 多项式回归模型的基本原理 多项式回归是线性回归的一种扩展,用于分析自变量 X X X与因变量 Y Y Y之间的非线性关系。与简单的线性回归模型不同,多项式回归模型通过引入自变量的高次项来增加模型的复杂度,从而能够拟合数据中的非线性模式。…...

「计算机网络」数据链路层
数据链路层的地位:网络中的主机、路由器等都必须实现数据链路层信道类型 点对点信道:使用一对一的点对点通信方式广播信道 使用一对多的广播通信方式必须使用专用的共享信道协议来协调这些主机的数据发送 使用点对点信道的数据链路层 数据链路和帧 链…...

【Linux】Ubuntu 22.04 升级 nodejs 到 v18
Ubuntu 22.04 已经安装的nodejs 版本 nodejs is already the newest version (12.22.9~dfsg-1ubuntu3.3). 删除以前的 nodejs 版本: 1. sudo apt remove nodejs rooterp:~# sudo apt remove nodejs Reading package lists... Done Building dependency tree..…...

当go get获取不到软件包时
当使用go get命令获取软件包时,如果无法成功获取,您可以尝试以下方法来解决问题: 检查网络连接:首先,确保您的计算机能够访问互联网,并且没有任何网络防火墙或代理设置阻止了go get命令的正常运行。 设置代…...

全网最详细解法|同济大学|高等数学|第八版|习题1-5
文章目录 全网最详细解法|同济大学|高等数学|第八版|习题1-5|5.1全网最详细解法|同济大学|高等数学|第八版|习题1-5|5.2 全网最详细解法|同济大学…...
可视化工具:将多种数据格式转化为交互式图形展示的利器
引言 在数据驱动的时代,数据的分析和理解对于决策过程至关重要。然而,不同的数据格式和结构使得数据的解读变得复杂和困难。为了解决这个问题,一种强大的可视化工具应运而生。这个工具具有将多种数据格式(包括JSON、YAML、XML、C…...
[嵌入式AI从0开始到入土]14_orangepi_aipro小修补含yolov7多线程案例
[嵌入式AI从0开始到入土]嵌入式AI系列教程 注:等我摸完鱼再把链接补上 可以关注我的B站号工具人呵呵的个人空间,后期会考虑出视频教程,务必催更,以防我变身鸽王。 第1期 昇腾Altas 200 DK上手 第2期 下载昇腾案例并运行 第3期 官…...
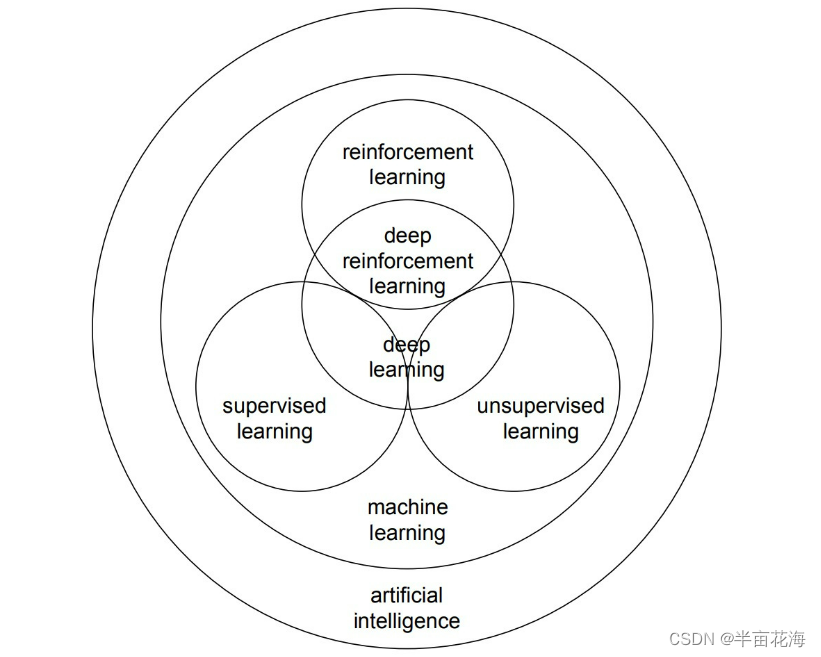
机器学习、深度学习、强化学习、迁移学习的关联与区别
Hi,大家好,我是半亩花海。本文主要了解并初步探究机器学习、深度学习、强化学习、迁移学习的关系与区别,通过清晰直观的关系图展现出四种“学习”之间的关系。虽然这四种“学习”方法在理论和应用上存在着一定的区别,但它们之间也…...

苹果为什么需要台积电3nm工艺芯片?
据《经济日报》报道,苹果公司的产品线将迎来重大升级。下一代应用于iPad、MacBook和iPhone的M4和A18处理器预计将会增加内置AI计算核心的数量,从而大幅提高AI运算能力。这一变化将导致对台积电(TSMC)订单的显著增长。据悉…...

力扣:53. 最大子数组和
解题思路: 1.先把数组为空和数组的长度为1时的特殊情况分别开来。声明一个sum变量用于计算数组中的连续子数组的总和值 。在声明一个guo变量用于一种接收sum中的前i-1的总和。另一种接收sum中前i的总和,主要根据sum的值来判断是接收的哪一种。在声明一个…...
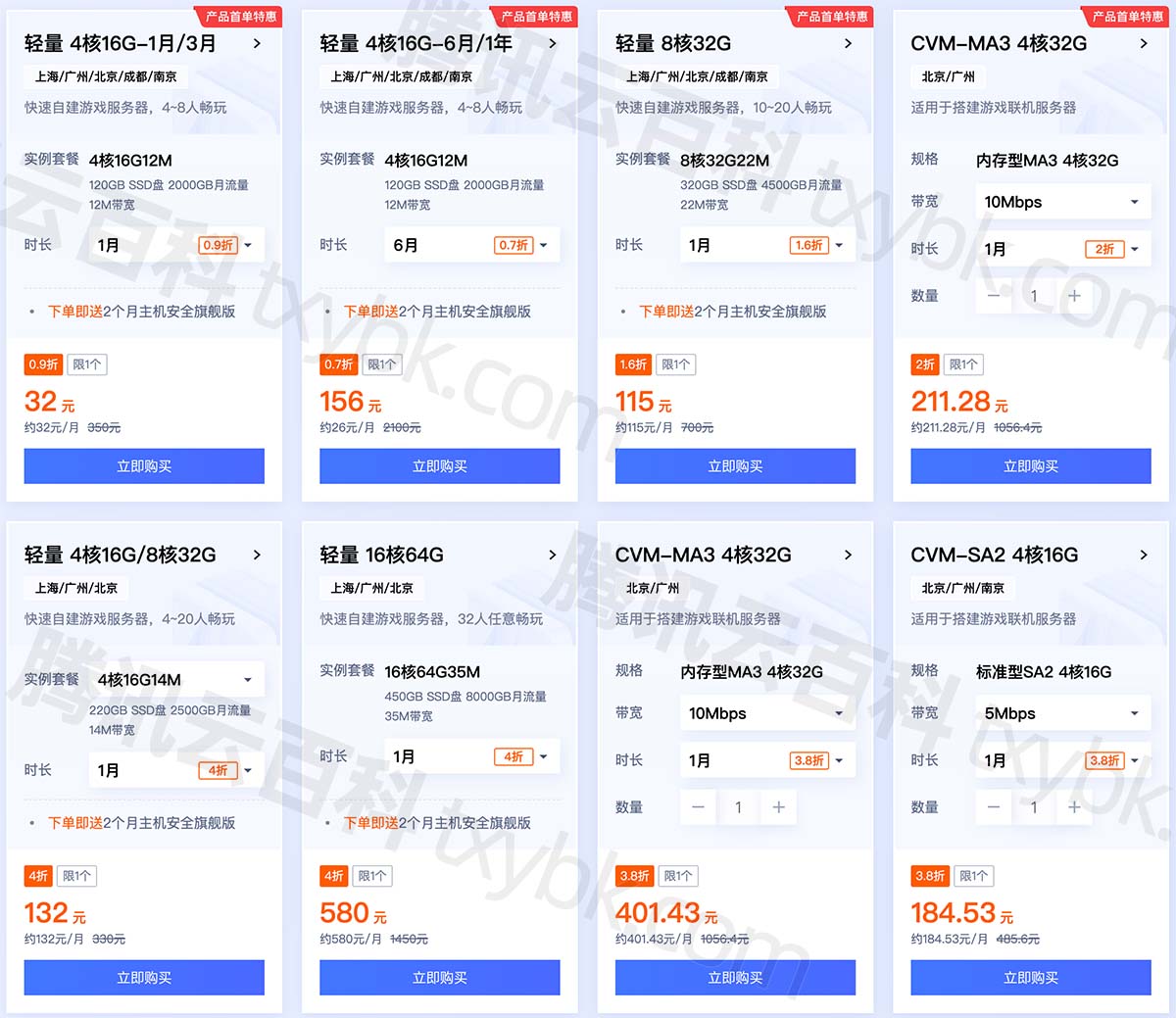
幻兽帕鲁Palworld专用服务器CPU内存配置怎么选择?
腾讯云幻兽帕鲁服务器配置怎么选?根据玩家数量选择CPU内存配置,4到8人选择4核16G、10到20人玩家选择8核32G、2到4人选择4核8G、32人选择16核64G配置,腾讯云百科txybk.com来详细说下腾讯云幻兽帕鲁专用服务器CPU内存带宽配置选择方法ÿ…...

学习总结11
KMP算法 全称Knuth-Morris-Pratt算法,是一种字符串匹配算法。该算法的目的是在一个文本串S内查找一个模式串P的出现位置。 KMP算法的核心思想是利用模式串自身的特性来避免不必要的字符比较。算法通过构建一个部分匹配表(也称为next数组)&a…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
