算法详解(力扣141——环形链表系列)
博主ID:代码小豪
文章目录
- 环形链表
- 环形链表的性质分析
- 快慢指针法
- 指针的追及相遇问题
- 环形链表(2)
环形链表
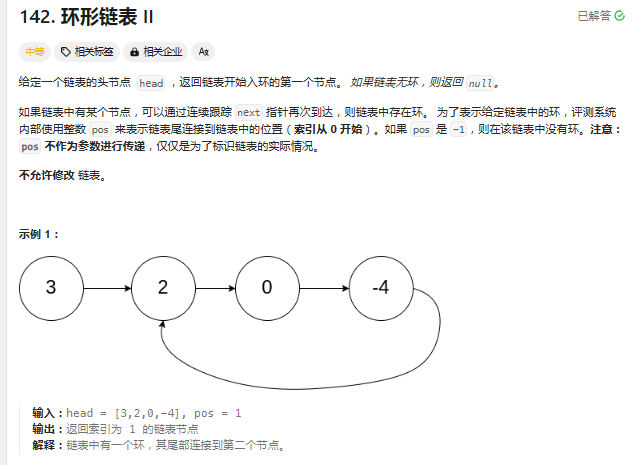
先来看看环形链表的原题:

中间的部分叙述有点繁杂,简单来概括就是,假如有一个节点,如果一直调用该节点的next,最后会回到该节点,那么这个链表就是带环的。
环形链表的性质分析
假如有个cur指针从头开始遍历链表,如果这个链表不是环形链表,那么这个cur指针会遍历至NULL指针处
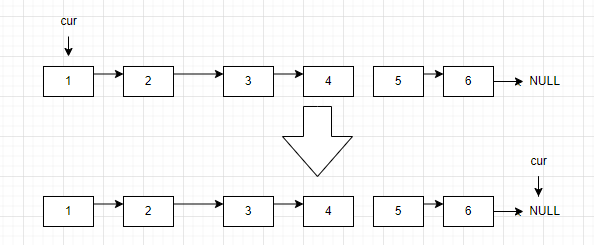
那么让一个指针从头开始遍历整个链表,如果这个指针到了NULL,就说明这个链表,不是环形链表。
while (cur){cur = cur->next;}return false;
但是如果这个链表是环形链表该如何证明呢?因为环形链表中是不在空节点的(NULL)。如果cur一直遍历,那么迭代就会进入死循环
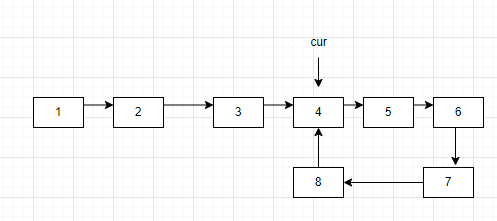
解决思路就是在环形链表当中加入一个标志指针,让这个指针处于环形处。
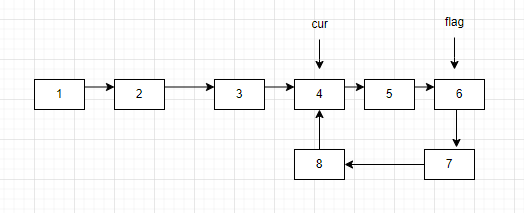
这样子让cur指针继续遍历链表,最后一定会遇上flag指针,证明这个链表是环形链表
快慢指针法
那么问题来了,如何让flag指针处于环内呢?因为如果计算机知道flag处于什么位置是环内,我又何必写一大堆代码证明这个链表是环形链表呢?而且如果这个链表不带环,那么flag又应该在什么位置呢?
为了解决这个问题,我们可以设置两个指针指向第一个节点,一个是快指针fast,一个是慢指针slow,让快指针一次递进多个节点,而慢指针依次递进一个节点,让这个操作进行循环。
如此操作,会发生两种情况
情况1,链表为非带环链表,fast指针来到空节点处(NULL),返回false
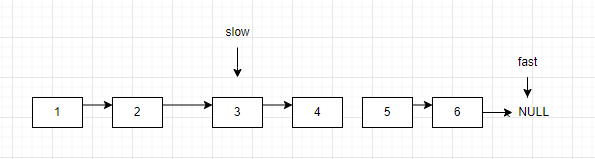
情况2,链表为带环链表,fast指针会一直循环遍历环形链表。slow一定会进入环内。
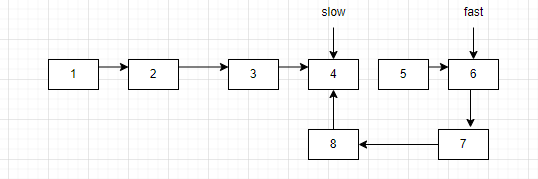
fast会在链表内循环遍历,所以fast有可能会和slow重合,如果fast和slow重合了,就说明这个链表是环形链表。
指针的追及相遇问题
通过前面前面分析可知,如果该链表是环形链表,那么快指针就有可能在环内与慢指针相遇,那么会不会发生快慢指针不会相遇的情况呢?
首先快指针一定是比慢指针移动更快的,我们假设快指针每次移动两个节点,慢指针每次移动一个节点。
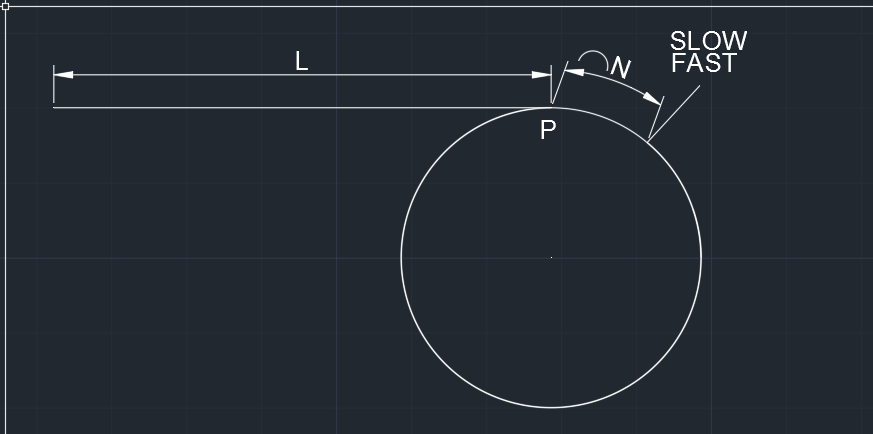
我们假设现在有一个环形链表,这个链表的入口点为点P。
设慢指针来到入口p时,快指针与慢指针的距离为N
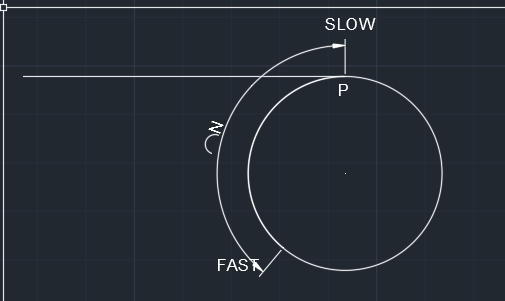
慢指针走一步,快指针会走两步,因此这两个指针的距离会随着执行次数,每次减一(慢指针的走1步,快指针的会走2步,那么快指针相距慢指针就近了一步)。
| 次数 | 距离 |
|---|---|
| 0 | N |
| 1 | N-1 |
| 2 | N-2 |
| 依此类推 | |
| N-2 | 2 |
| N-1 | 1 |
| N | 0 |
可以发现,如果快指针走两步,慢指针走一步,那么这两个指针一定会在环中相遇。
那么如果快指针一次移动三个节点,慢指针一次移动一个节点,我们能得出什么样的结论呢?
还是假设当慢指针到达入口点距离快指针的距离为N
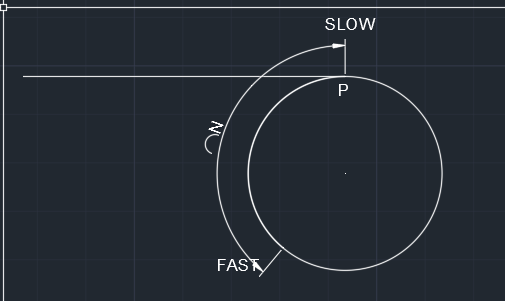
当慢指针与快指针的距离N为偶数时
| 次数 距离 | |
|---|---|
| 0 | N |
| 1 | N-2 |
| 2 | N-4 |
| 依次类推 | |
| N/2-1 | 2 |
| N/2 | 0 |
当N为偶数时,快慢指针会相遇
当快指针与慢指针之间的距离为奇数时
| 次数 距离 | |
|---|---|
| 0 | N |
| 1 | N-2 |
| 2 | N-4 |
| 依次类推 | |
| N/2-1 | 1 |
| N/2 | -1 |
可以发现快指针会越过慢指针,此时快指针会比慢指针多一个节点左右的距离,快指针需要再次遍历整个环形链表,直到与慢指针相遇。
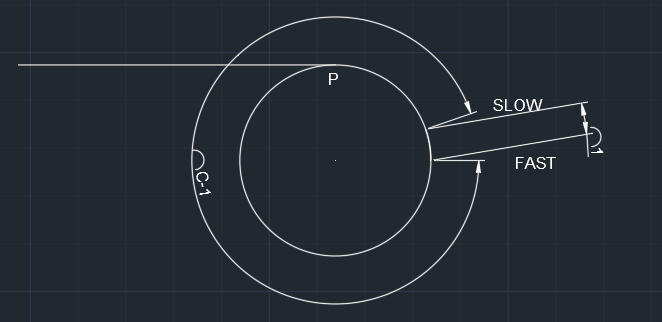
设环形链表的周长为C,那么此时快指针与慢指针的距离为C-1.
当C为奇数时,C-1为偶数
那么程序的运行次数与快慢指针的距离关系为
| 次数 距离 | |
|---|---|
| 0 | C-1 |
| 1 | C-3 |
| 2 | C-5 |
| 依次类推 | |
| (C-1)/2-1 | 2 |
| (C-1)/2 | 0 |
由此推出,当N为奇数,C为奇数时,快指针最后会追上慢指针。
当C为偶数时,C-1为奇数
| 次数 距离 | |
|---|---|
| 0 | C-1 |
| 1 | C-3 |
| 2 | C-5 |
| 依次类推 | |
| (C-1)/2-1 | 1 |
| (C-1)/2 | -1 |
可以发现快指针和慢指针的距离在这一次追及之后,快慢指针的距离又回到了C-1。所以当N为奇数,C为偶数(C-1为奇数)时,快指针走三个节点,慢指针走1个节点的方式会永远不会相遇。
综上所述,如果我们想用快慢指针相遇的方式证明环形链表,最好的方法是让快指针一次后进两个节点,而慢指针一次后进一个节点。
当快指针后进多个(大于等于2)的节点时,有可能会出现快慢指针永远无法相遇的情况。比如当快指针后进3个节点时,如果此时N为奇数,C为偶数时,快指针永远无法与慢指针相遇,从而导致死循环的出现
解题代码如下:
bool hasCycle(struct ListNode *head) {if(head==NULL)return false;struct ListNode*slow=head;struct ListNode*fast=head->next;while(fast){if(fast->next==NULL)return false;fast=fast->next->next;slow=slow->next;if(fast==slow)return true;}return false;
}
环形链表(2)
这是前面环形链表的变形体,这个OJ的要求是这样的:假设这是一个环形链表,那么就要找到这个链表的入口节点,并将这个节点返回。如果是非环形链表,则返回NULL指针。
首先,我们将这个问题的实现分为两个部分,第一、我们要先确定这是一个环形链表,然后,我们求出这个环形链表的入口点。
确定环形链表的方法已经说明过了,现在要思考的是如何找到这个入口点。
我们首先来思考一下快慢指针的位移关系,已知,快指针的速度是慢指针的两倍,因此当慢指针来到入口点L时,快指针已经移动2L了。
我们假设从链表头到入口点的距离为L,从入口点到达相遇点的距离为N,环形链表的周长为C。
如果L>C。假如slow移动了L的距离来到入口点,可以知道fast移动距离为2L,在圈内循环了x圈(x至少为1)
当slow来到相遇点时,那么slow移动的距离是L+N,而fast移动的距离为L+N+(x+1)C。
如果L<C。假如slow移动了L的距离来到入口点,可以知道fast移动距离为2L,在圈内循环了0圈
当slow来到相遇点时,那么slow移动的距离是L+N,而fast移动的距离为L+N+C。
根据fast的位移是slow的两倍可以得出:
当L>C时,2(L+N)=L+N+(x+1)C。
当L<C时,2(L+N)=L+N+C。
可以合并成一个公式:
2(L+N)=L+N+yC。(y>=1).
合并同类项得L=yC-N。
我们可以图中明显的看出一个关系
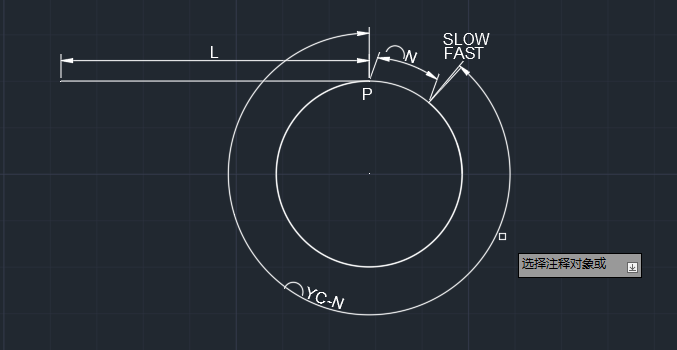
如果一个指针从相遇点移动YC-N个节点时,会来到入口点。而且一个指针从链表头开始移动L位时,回来到入口点。
并且L=yC-N。
可以得出,如果让一个指针从链表头开始移动,一个指针从相遇点开始移动。这两个指针会在入口点相遇。
代码如下:
struct ListNode *detectCycle(struct ListNode *head) {struct ListNode*fast=head;struct ListNode*slow=head;while(fast){if(fast->next==NULL)return NULL;fast=fast->next->next;slow=slow->next;if(fast==slow){struct ListNode*meet=slow;while(meet!=head){meet=meet->next;head=head->next;} return meet;}}return NULL;
}
相关文章:

算法详解(力扣141——环形链表系列)
博主ID:代码小豪 文章目录 环形链表环形链表的性质分析快慢指针法指针的追及相遇问题 环形链表(2) 环形链表 先来看看环形链表的原题: 中间的部分叙述有点繁杂,简单来概括就是,假如有一个节点,…...
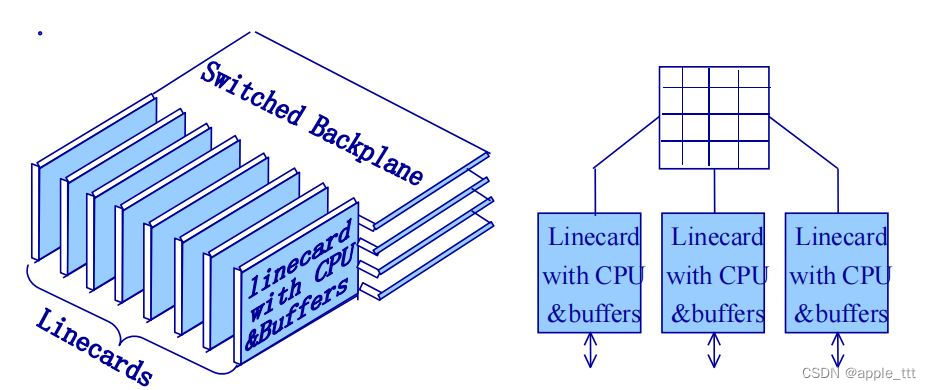
浅谈路由器交换结构
一、路由器技术概述 路由器(Router)是连接两个或多个网络的硬件设备,在网络间起网关的作用,是读取每一个数据包中的地址然后决定如何传送的专用智能性的网络设备。它能够理解不同的协议,例如某个局域网使用的以太网协议…...
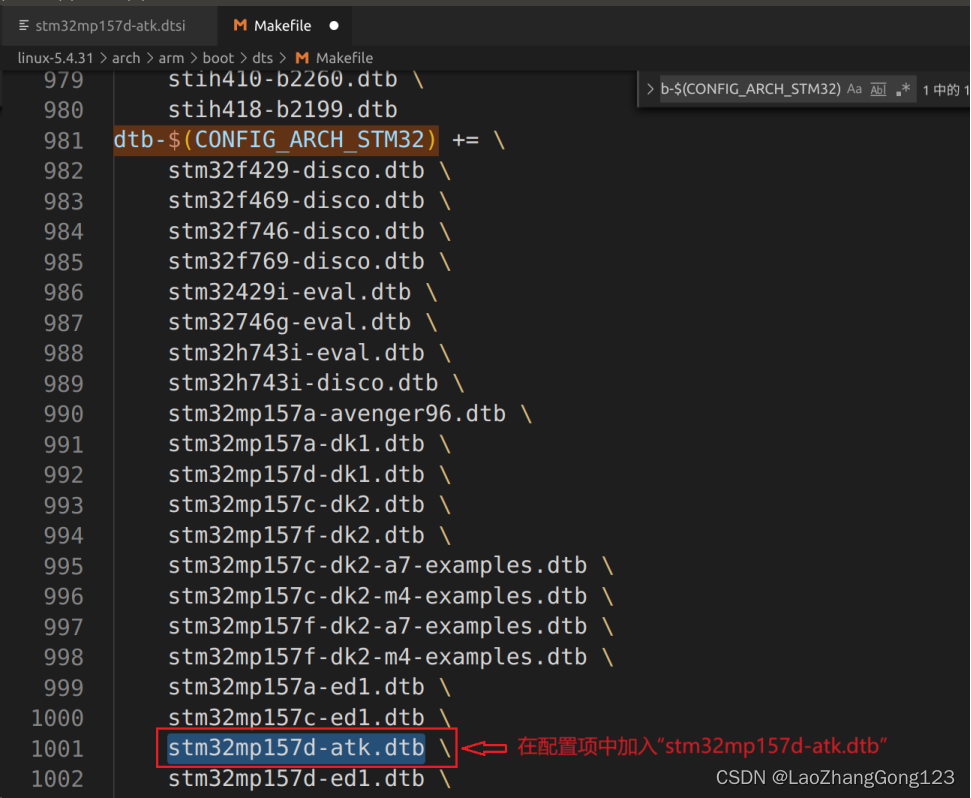
Linux第51步_移植ST公司的linux内核第3步_添加修改设备树
1、设备树文件的路径 1)、创建linux中的设备树头文件 在“my_linux/linux-5.4.31/arch/arm/boot/dts/”目录中,以“stm32mp15xx-edx.dtsi”为蓝本,复制一份,并命名为 “stm32mp157d-atk.dtsi”,这就是我们开发板的设备树头文件。…...
统计操作)
【PyTorch】PyTorch中张量(Tensor)统计操作
PyTorch深度学习总结 第五章 PyTorch中张量(Tensor)统计操作 文章目录 PyTorch深度学习总结前言一、最值查找二、特殊值查询 前言 上文介绍了PyTorch中张量(Tensor)的计算操作,本文将介绍张量的统计操作。 一、最值查找 函数描述torch.max()找出张量中的最大值to…...
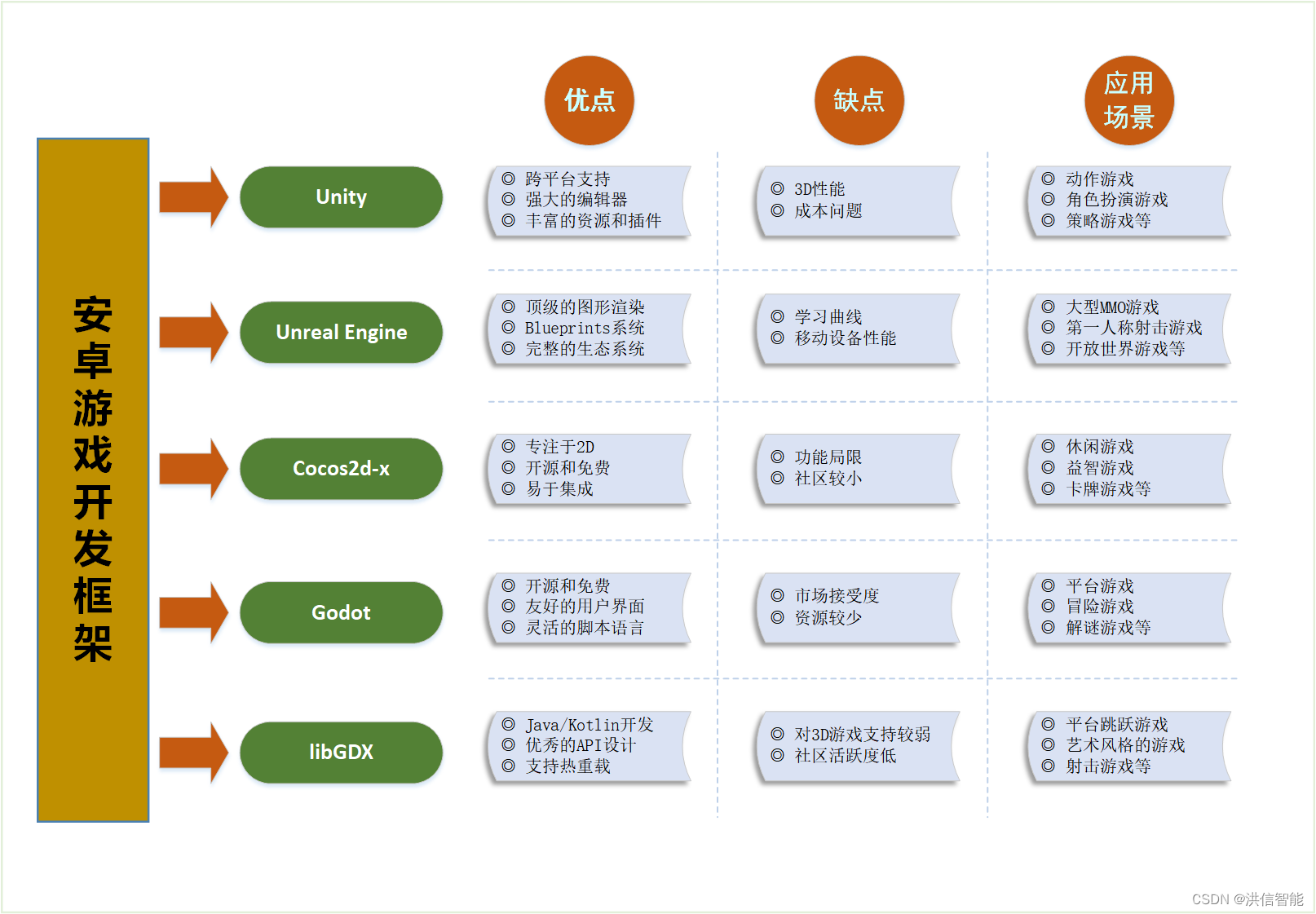
安卓游戏开发框架应用场景以及优劣分析
一、引言 在移动游戏开发领域,选择合适的开发框架是项目成功的关键因素之一。特别是对于安卓平台,由于其开放性和庞大的用户基础,不同的游戏开发框架应运而生,旨在帮助开发者高效地构建游戏应用。以下是一些流行的安卓游戏开发框架…...
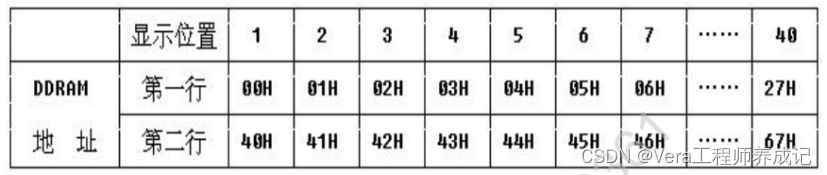
单片机学习笔记---LCD1602
LCD1602介绍 LCD1602(Liquid Crystal Display)液晶显示屏是一种字符型液晶显示模块,可以显示ASCII码的标准字符和其它的一些内置特殊字符(比如日文的片假名),还可以有8个自定义字符 显示容量:…...

django中实现适配器模式
在Django中实现适配器模式(Adapter Pattern)涉及到创建一个适配器类,它允许不兼容的接口之间进行交互。适配器模式通常用于将一个类的接口转换为另一个客户端期望的接口。 一:实现例子 下面是一个简单的例子,演示如何…...
--EXCEL排序)
题记(42)--EXCEL排序
目录 一、题目内容 二、输入描述 三、输出描述 四、输入输出示例 五、完整C语言代码 一、题目内容 Excel可以对一组纪录按任意指定列排序。现请你编写程序实现类似功能。 对每个测试用例,首先输出1行“Case i:”,其中 i 是测试用例的编号&#…...

【学网攻】 第(28)节 -- OSPF虚链路
系列文章目录 目录 系列文章目录 文章目录 前言 一、什么是OSPF虚链路? 二、实验 1.引入 实验目标 实验背景 技术原理 实验步骤 实验设备 实验拓扑图 实验配置 扩展 实验拓扑图 实验配置 实验验证 文章目录 【学网攻】 第(1)节 -- 认识网络【学网攻…...

百面嵌入式专栏(面试题)驱动开发面试题汇总1.0
沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇我们将介绍驱动开发面试题 。 1、Linux驱动程序的功能是什么? 对设备初始化和释放。进行内核与硬件的数据交互。检测和处理设备出现的错误。2、内核程序中申请内存使用什么函数? 答案:kmalloc()、kzalloc()、vm…...

Starknet 的 JavaScript 库:Starknet.js、get-starknet和starknet-react
文章目录 Starknet 的 JavaScript 库Starknet.jsget-starknetstarknet-reactStarknet 的 JavaScript 库Starknet.js 官方:https://www.starknetjs.com/ Starknet.js 是一个与 Starknet 交互的 JavaScript 库,通常以脚本或去中心化形式进行交互应用程序。 Starknet.js 的灵感…...
)
debian11 安装 k8s,containerd ,阿里云镜像(已成功)
1. 环境准备 系统要求:至少 2GB RAM(建议 4GB 或更多),网络连接。 节点准备:至少 3 台机器,1 台作为 Master 节点,2 台作为 Worker 节点。 安装sudo apt update apt install sudo设置主机名&a…...

Spring Task定时任务
目录 1、介绍 2、cron表达式 2.1、在线生成器 2.2、通配符 3、代码示例 3.1、使用步骤 3.2、 代码开发 3.3、测试 🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发…...

【设计模式】23中设计模式笔记
设计模式分类 模板方法模式 核心就是设计一个部分抽象类。 这个类具有少量具体的方法,和大量抽象的方法,具体的方法是为外界提供服务的点,具体方法中定义了抽象方法的执行序列 装饰器模式 现在有一个对象A,希望A的a方法被修饰 …...

类加载过程介绍
一、类的生命周期 类被加载到jvm虚拟机内存开始,到卸载出内存为止,他的生命周期可以分为:加载->验证->准备->解析->初始化->使用->卸载。 其中验证、准备、解析统一称为链接阶段 1、加载 将类的字节码载入方法区中…...

pytorch创建模型方式
1.继承自nn.Module的方式 from torch import nn import torch.nn.functional as F 继承自nn.Moduleclass LModel(nn.Module):def __init__(self):super().__init__()self.L1 nn.Linear(10,10)self.L2 nn.Linear(10,64)self.L3 nn.Linear(64,10)self.L4 nn.Linear(10,5)se…...
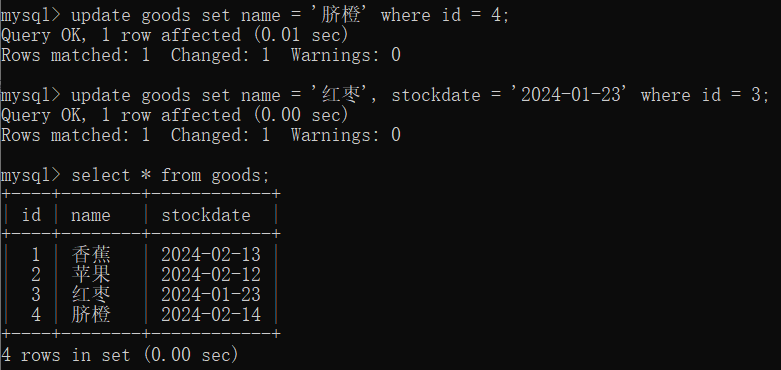
MySQL 基础知识(五)之数据增删改
目录 1 插入数据 2 删除数据 3 更改数据 创建 goods 表 drop table if exists goods; create table goods ( id int(10) primary key auto_increment, name varchar(14) unique, stockdate date )charsetutf8; 1 插入数据 当要插入的数据为日期/时间类型时,如果…...

紫微斗数双星组合:廉贞天府在辰戌
文章目录 前言内容总结 前言 紫微斗数双星组合:廉贞天府在辰戌 内容 紫微斗数双星组合:廉贞天府在辰戌 性格分析 廉贞天府同坐辰、戌宫,若无煞星冲破,为“天府朝垣格”,也为“府相朝垣格”,富贵双全&am…...

人工智能|深度学习——基于全局注意力的改进YOLOv7-AC的水下场景目标检测系统
代码下载: 基于全局注意力的改进YOLOv7-AC的水下场景目标检测系统.zip资源-CSDN文库 1.研究的背景 水下场景目标检测是水下机器人、水下无人机和水下监控等领域中的重要任务之一。然而,由于水下环境的复杂性和特殊性,水下目标检测面临着许多挑…...
:最简CPU)
使用 C++23 从零实现 RISC-V 模拟器(1):最简CPU
👉🏻 文章汇总「从零实现模拟器、操作系统、数据库、编译器…」:https://okaitserrj.feishu.cn/docx/R4tCdkEbsoFGnuxbho4cgW2Yntc 本节实现一个最简的 CPU ,最终能够解析 add 和 addi 两个指令。如果对计算机组成原理已经有所了…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
