备战蓝桥杯---图论之最短路Bellman-Ford算法及优化
目录
上次我们讲到复杂度为(n+m)logm(m为边,n为点)的迪杰斯特拉算法,其中有一个明显的不足就是它无法解决包含负权边的图。
于是我们引进Bellman-Ford算法。
核心:枚举所有的点,能松弛就松弛,直到所有点都不能松弛。
具体过程:
我们在外循环循环n-1(n为点数),然后在内循环上枚举所有的边,能松弛就松弛。
到这里,肯定有许多人对它正确性怀疑,其实,我们可以知道,在外循环循环k轮后,k步以内可以到的点的值<=从源点在k步以内能走到的最优解(有点类似广搜)。
具体来说,当k=2时,2步以内可以到的点的值<=2步内从源点走到该点的最小距离。(<=的原因在于枚举边的时候可能会被刚刚更新的点在被更新一遍)
上次我们讲到复杂度为(n+m)logm(m为边,n为点)的迪杰斯特拉算法,其中有一个明显的不足就是它无法解决包含负权边的图。
于是我们引进Bellman-Ford算法。
核心:枚举所有的点,能松弛就松弛,直到所有点都不能松弛。
具体过程:
我们在外循环循环n-1(n为点数),然后在内循环上枚举所有的边,能松弛就松弛。
到这里,肯定有许多人对它正确性怀疑,其实,我们可以知道,在外循环循环k轮后,k步以内可以到的点的值<=从源点在k步以内能走到的最优解(有点类似广搜)。
具体来说,当k=2时,2步以内可以到的点的值<=2步内从源点走到该点的最小距离。(<=的原因在于枚举边的时候可能会被刚刚更新的点在被更新一遍)
因此,在n-1轮后,因为每一个点最多被走一次(除非是负环,等下讨论),因此,利用上述结论,我们可以得出在外循环循环n-1轮后,所有的点的值为从源点出发走到的最优解。
下面我们讨论一下负环,其实,如果出现负环,最短路就应该为负无穷,我们为了判断负环,只要比较更新次数有无<=n-1即可。
因为这过于暴力,复杂度为o(n*m),基本一用就寄,于是我们考虑一下优化
我们不妨思考一个问题(这也是优化的关键)
一个点在什么情况下可以优化?
显然,只有到它的前一个点它的值优化改变后,那个点才可能被优化。因为边权是不变的,而前一个点它的值无法被优化时,dis[a]=map[a][b]+dis[b],相当于dis[b]不变,那么dis[a]肯定也不变。
在知道这个后,我们让dis[源点]=0,其他为极大值。
我们对于边的枚举,只要枚举上一次被更新的点的边就可以了。
我们用队列实现(即SPFA算法,复杂度为o(k*m)(k为每一个点入队的平均次数)
还是这一题,我们用这个方法实现一下。

下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
struct node{int zhi;int dian;int next;
}edge[20010];
int dis[1010],head[1010],cnt,n,m1,s,t,x,y,v;
bool vis[1010];
struct ty{int dian,dis1;bool operator<(const ty &a) const{return dis1>a.dis1;}
};
void merge(int x,int y,int v){edge[++cnt].zhi=v;edge[cnt].dian=y;edge[cnt].next=head[x];head[x]=cnt;
}
priority_queue<ty> q;
queue<int> q1;
int dij(int s,int t){q.push({s,0});while(!q.empty()){ty ck=q.top();q.pop();if(vis[ck.dian]==1) continue;vis[ck.dian]=1;for(int i=head[ck.dian];i!=-1;i=edge[i].next){int i1=edge[i].dian;if(vis[i1]==1) continue;if(dis[i1]>dis[ck.dian]+edge[i].zhi){dis[i1]=dis[ck.dian]+edge[i].zhi;q.push({i1,dis[i1]});}}}if(dis[t]>=0x3f3f3f3f) return -1;else return dis[t];
}
int spfa(int s,int t){q1.push(s);while(!q1.empty()){int hh=q1.front();vis[hh]=0;q1.pop();for(int i=head[hh];i!=-1;i=edge[i].next){int i1=edge[i].dian;if(dis[i1]>dis[hh]+edge[i].zhi){dis[i1]=dis[hh]+edge[i].zhi;if(vis[i1]==0){vis[i1]=1;q1.push(i1);}}}}if(dis[t]>=0x3f3f3f3f) return -1;else return dis[t];
}
int main(){cin>>n>>m1>>s>>t;memset(head,-1,sizeof(head));for(int i=1;i<=m1;i++){scanf("%d%d%d",&x,&y,&v);merge(x,y,v);merge(y,x,v);}memset(dis,0x3f,sizeof(dis));dis[s]=0;cout<<spfa(s,t);
}相关文章:

备战蓝桥杯---图论之最短路Bellman-Ford算法及优化
目录 上次我们讲到复杂度为(nm)logm(m为边,n为点)的迪杰斯特拉算法,其中有一个明显的不足就是它无法解决包含负权边的图。 于是我们引进Bellman-Ford算法。 核心:枚举所有的点,能松弛就松弛,直…...

C++ //练习 5.19 编写一段程序,使用do while循环重复地执行下述任务:首先提示用户输入两个string对象,然后挑出较短的那个并输出它。
C Primer(第5版) 练习 5.19 练习 5.19 编写一段程序,使用do while循环重复地执行下述任务:首先提示用户输入两个string对象,然后挑出较短的那个并输出它。 环境:Linux Ubuntu(云服务器&#x…...
算法刷题:有效三角形个数
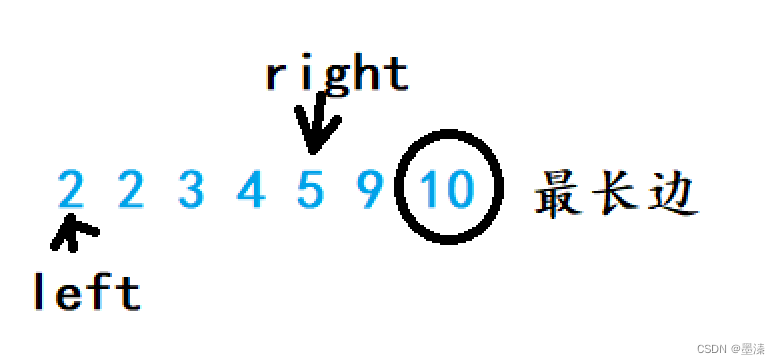
有效三角形个数 .题目链接题目详情算法原理补充知识点双指针:对撞指针 我的答案 . 题目链接 有效三角形个数 题目详情 算法原理 补充知识点 有效三角形需要满足的条件: ab>cac>bbc>a 其实在满足1的时候,c是最大的,那么2和3是显然成立的,因此我们可以这样解题: 对…...

python---变量
1.变量就是存储数据的空间,在内存上; 2.变量命名规则:(1)由数字,字母,下划线组成,数字不能开头; (2)不能和关键字冲突; (…...
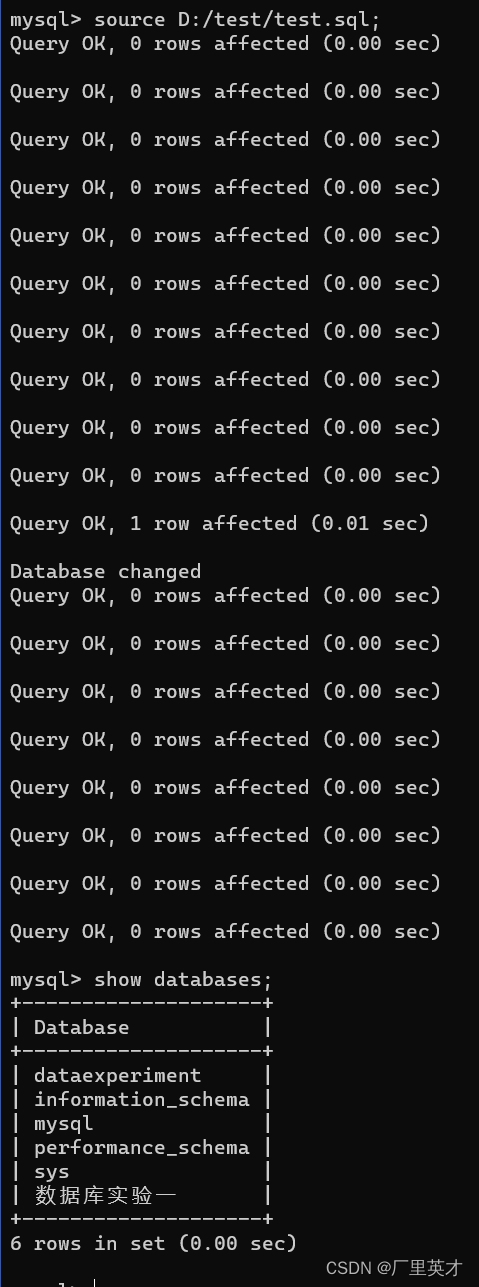
数据库第二次实验
目录 1 实验内容 2 SQL代码及运行截图 2.1 创建表并插入数据 2.1.1 创建表 2.1.2 插入数据 2.1.3 运行截图 2.2 修改表 2.2.1 SQL代码 2.2.2 运行截图 2.3 删除操作 2.3.1 SQL代码 2.3.2 运行截图 2.4 数据库的备份 2.5 数据库的恢复 1 实验内容 实验目的&#…...

容器高级知识:Kubernetes Pod 适配器模式详解
Kubernetes Pod 适配器(Adapter)模式详解 Kubernetes Pod 适配器模式是侧车(Sidecar)模式的一个特例,其中使用专用的 适配器容器 在主应用程序容器和其他服务或客户端之间 翻译 数据或信号。它充当桥梁,调整通信格式或协议以实现…...

云原生容器化-5 Docker常见操作命令
1.登录和退出docker仓库 使用docker login和docker logout分别用于登录和退出docker仓库。 #登录时携带用户名、密码、仓库地址信息 docker login --username test --password test123 192.168.0.22:8000 docker login --username seong --password 3er4#ER$ 192.168.0.22:8…...

几道简单的题目练一下手感
第 1 题 【 问答题 】 • 找和为K的两个元素 在一个长度为n(n < 1000)的整数序列中,判断是否存在某两个元素之和为k。 时间限制:1000 内存限制:65536 输入 第一行输入序列的长度n和k,用空格分开。 第二行输入序列中的n个整数&a…...
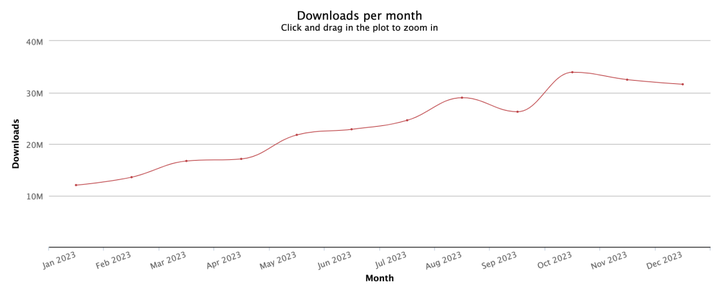
2023年哪个前端框架用的最多?
2023 年,TypeScript 的每月下载量持续稳定增长,年度累计下载量高达2,071,832,110(20.7 亿),展现了强大的市场需求和用户认可。 本文来通过详细的数据(2023 年 npm 累计下载量),看看…...
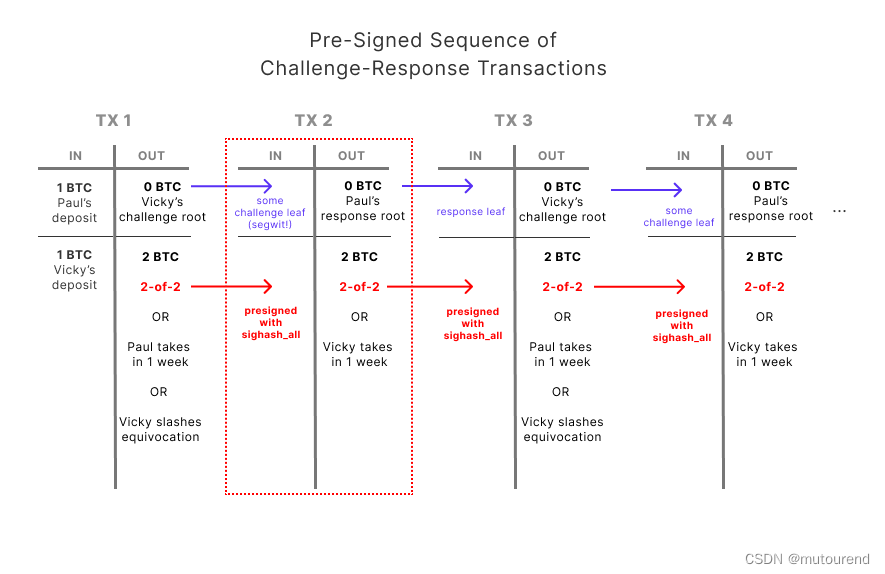
基于BitVM的乐观 BTC bridge
1. 引言 前序博客: 区块链互操作协议Bitcoin Bridge:治愈还是诅咒?BitVM:Bitcoin的链下合约 基于BitVM的乐观 BTC bridge: Trust-minimized two-way peg 机制 BitVM BTC bridge背后的主要思想是: 为比…...
谷歌浏览器安装扩展程序axure-chrome-extension
注: 文末附扩展附件:axure-chrome-extension_v0.7.0.crx 1、安装扩展程序axure-chrome-extension 找到axure-chrome-extension.crx,把axure-chrome-extension.crx后缀改为zip,然后解压,得到一个文件夹 2、打开谷歌浏览…...

C++学习:大小写转换
islower/isupper函数 islower和isupper是C标准库中的字符分类函数,用于检查一个字符是否为小写字母或大写字母。 islower和isupper函数需要包含头文件,也可用万能头文<bits/stdc.h>包含。 函数返回值为bool类型。 char ch1 A; char ch2 a;//…...

【王道数据结构】【chapter5树与二叉树】【P159t16】
试设计判断两棵二叉树是否相似的算法。所谓二叉树T1和T2相似,指的是T1和T2都是空的二叉树或都只有一个根节点;或者T1的左子树和T2的左子树是相似的,且T1的右子树和T2的右子树是相似的 #include <iostream> #include <stack> #inc…...

代码随想录算法训练营第51天 | 139.单词拆分 多重背包理论基础
单词拆分 这道题最后是判断能否组成,很像回溯法的问题形式,和分割回文串那道题比较类似,所以是可以用回溯法解决的,但是回溯法需要使用记忆化递归来避免超时。 class Solution{ public:bool backtracking(const string s, const …...

weilai8游戏爬虫
#!/usr/bin/python # -*- coding: UTF-8 -*- #!/usr/bin/python # -*- coding: UTF-8 -*- import os,csv import re import random import time import requests from lxml import etreefrom urllib.parse import quote, unquotepage98 sess requests.Session()#创建一个sessi…...
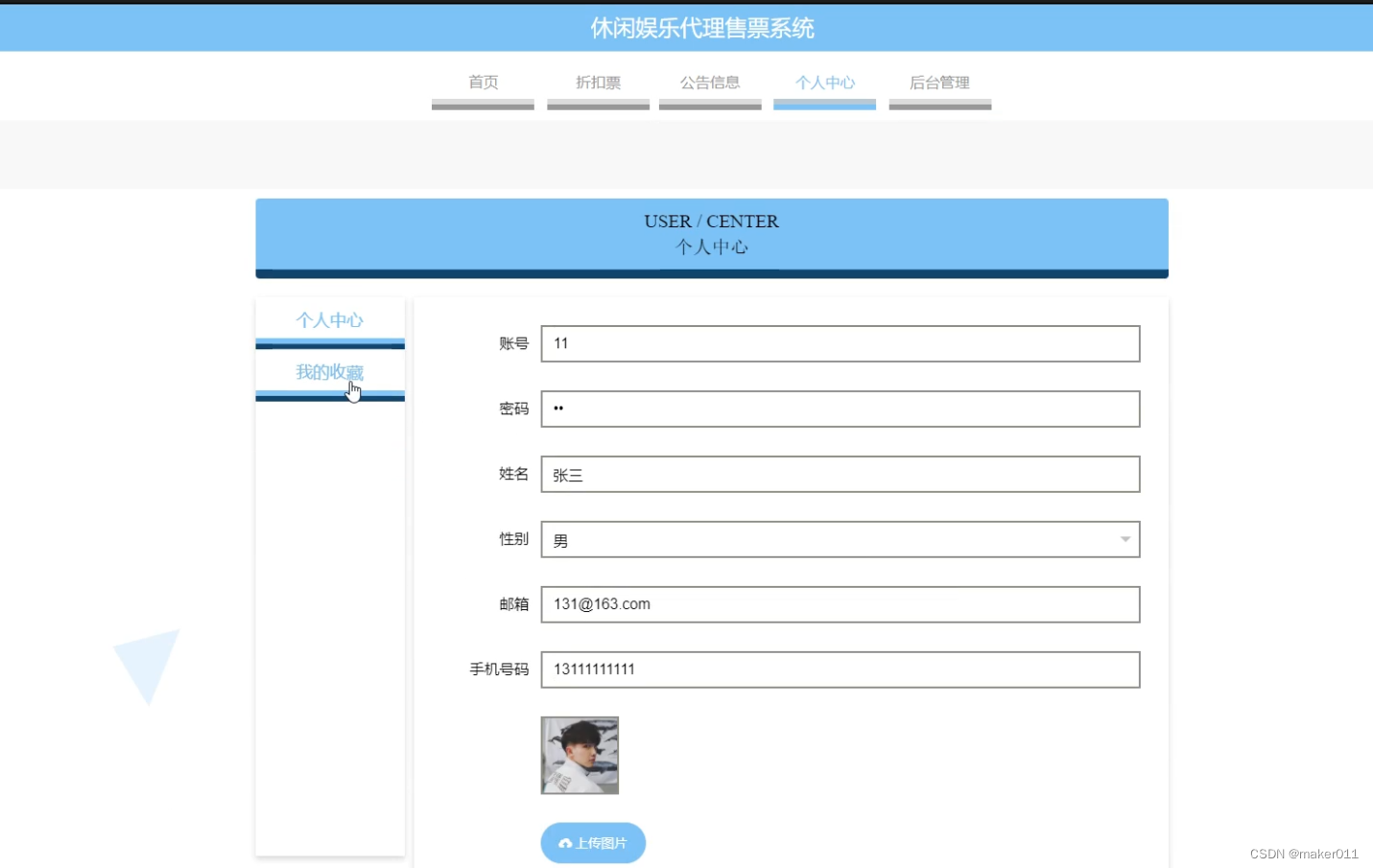
【Java程序设计】【C00261】基于Springboot的休闲娱乐代理售票系统(有论文)
基于Springboot的休闲娱乐代理售票系统(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的休闲娱乐代理售票系统 本系统分为系统功能模块、管理员功能模块以及用户功能模块。 系统功能模块:休闲娱乐代理…...
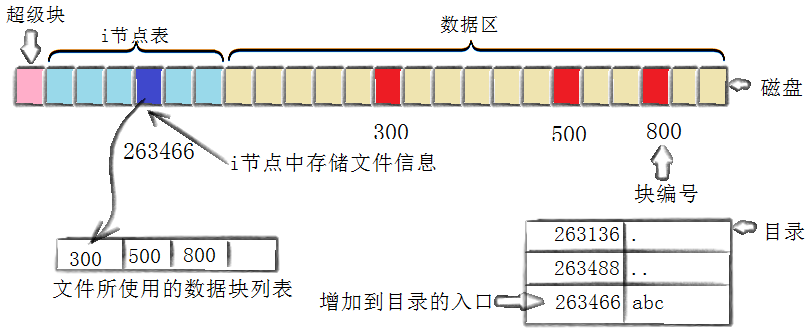
【Linux】学习-基础IO拓展篇
Linux基础IO拓展篇—详解文件系统 理解文件系统 在Linux基础IO篇中,我们站在用户的视角对文件进行了理解,主要是针对被打开的文件,那么有没有没有被打开的文件呢?当然有!今天我们换个视角,来站在系统的角…...
算法详解(力扣141——环形链表系列)
博主ID:代码小豪 文章目录 环形链表环形链表的性质分析快慢指针法指针的追及相遇问题 环形链表(2) 环形链表 先来看看环形链表的原题: 中间的部分叙述有点繁杂,简单来概括就是,假如有一个节点,…...
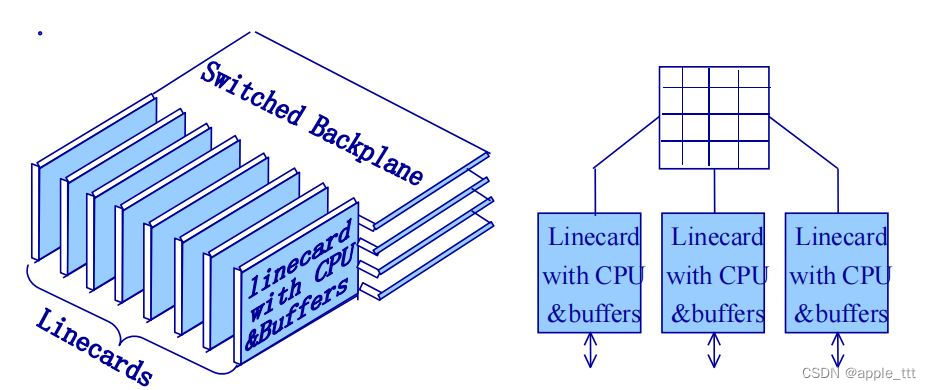
浅谈路由器交换结构
一、路由器技术概述 路由器(Router)是连接两个或多个网络的硬件设备,在网络间起网关的作用,是读取每一个数据包中的地址然后决定如何传送的专用智能性的网络设备。它能够理解不同的协议,例如某个局域网使用的以太网协议…...
Linux第51步_移植ST公司的linux内核第3步_添加修改设备树
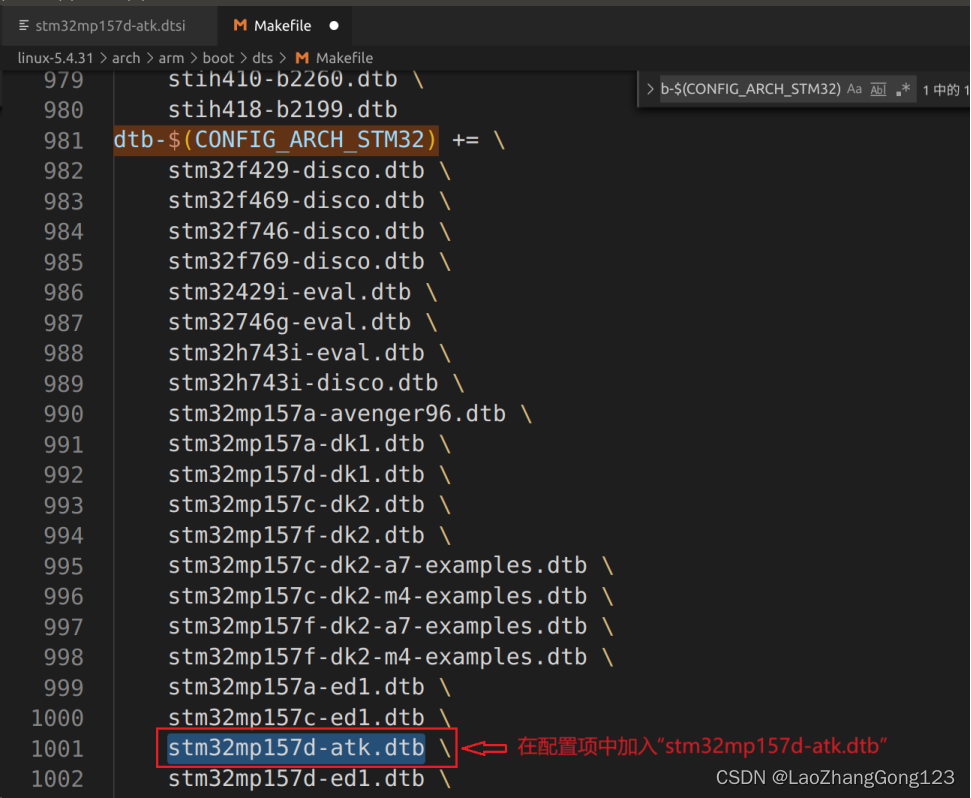
1、设备树文件的路径 1)、创建linux中的设备树头文件 在“my_linux/linux-5.4.31/arch/arm/boot/dts/”目录中,以“stm32mp15xx-edx.dtsi”为蓝本,复制一份,并命名为 “stm32mp157d-atk.dtsi”,这就是我们开发板的设备树头文件。…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...
