Duilib List 控件学习
这是自带的一个示例;
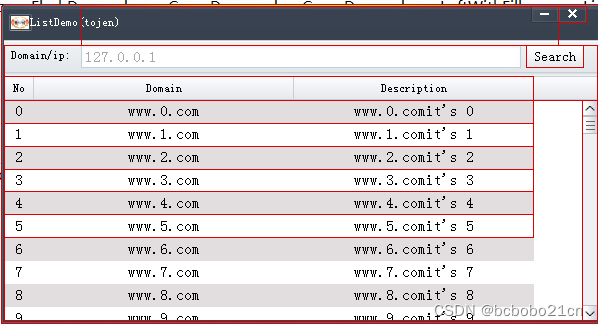
一开始运行的时候List中是空的,点击Search按钮以后就填充列表框;
先看一下列表框列头是在xml文件中形成的;
<List name="domainlist" bkcolor="#FFFFFFFF" ... menu="true">
<ListHeader height="24" menu="true">
<ListHeaderItem text="No" ... sepwidth="1"/>
<ListHeaderItem text="Domain" ... sepwidth="1"/>
<ListHeaderItem text="Description" ... sepwidth="1"/>
</ListHeader>
</List>
WinMain里面主要是读取资源文件,创建主框架窗口;
然后看一下Search按钮相关的;
此按钮在xml文件中的name为"btn";
在代码中使用如下一句,
m_pSearch = static_cast<CButtonUI*>(m_pm.FindControl(_T("btn"))
相关文章:

Duilib List 控件学习
这是自带的一个示例; 一开始运行的时候List中是空的,点击Search按钮以后就填充列表框; 先看一下列表框列头是在xml文件中形成的; <List name="domainlist" bkcolor="#FFFFFFFF" ... menu="true"> <ListHeader height="24…...

详细了解Node.js的配置与使用!
详细了解Node.js的配置与使用! Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。它允许开发者在服务器端运行 JavaScript,从而实现全栈 JavaScript 开发。本文将介绍 Node.js 的配置和 npm 的应用。 一、Node.js 配置 下载与安装 首先&…...

OpenCV 移动最小二乘图像变形
文章目录 一、简介二、实现代码三、实现效果参考文献一、简介 在现实生活中,我们常常应用一些刚性的变换来实现物体的旋转平移,对于非刚性的变换我们都没有在意,其实这种变换也是无处不在的,如我们经常看的动画就可以通过一些非刚性的变换达到一些非常夸张的效果。这里,我…...

【深度学习】S2 数学基础 P4 概率论
目录 基本概率论概率论公理随机变量 多个随机变量联合概率条件概率贝叶斯定理求和法则独立性 期望与方差小结 基本概率论 机器学习本质上,就是做出预测。而概率论提供了一种量化和表达不确定性水平的方法,可以帮助我们量化对某个结果的确定性程度。 在…...

跟我学c++中级篇——静态多态
一、多态 Polymorphism,多态。学习过c的人如果不知道多态,基本上就是打入c内部的C程序员了。在前边曾经对多态进行过分析,对其中的虚函数(虚表等)也进行过较为详细的说明。 多态其实非常好理解,不要硬扣书…...
)
设计模式--桥接模式(Bridge Pattern)
桥接模式(Bridge Pattern)是一种结构型设计模式,它主要是用于将抽象部分与实现部分分离,使它们可以独立地变化。 桥接模式主要包含以下几个角色: Abstraction(抽象类):定义抽象类的…...
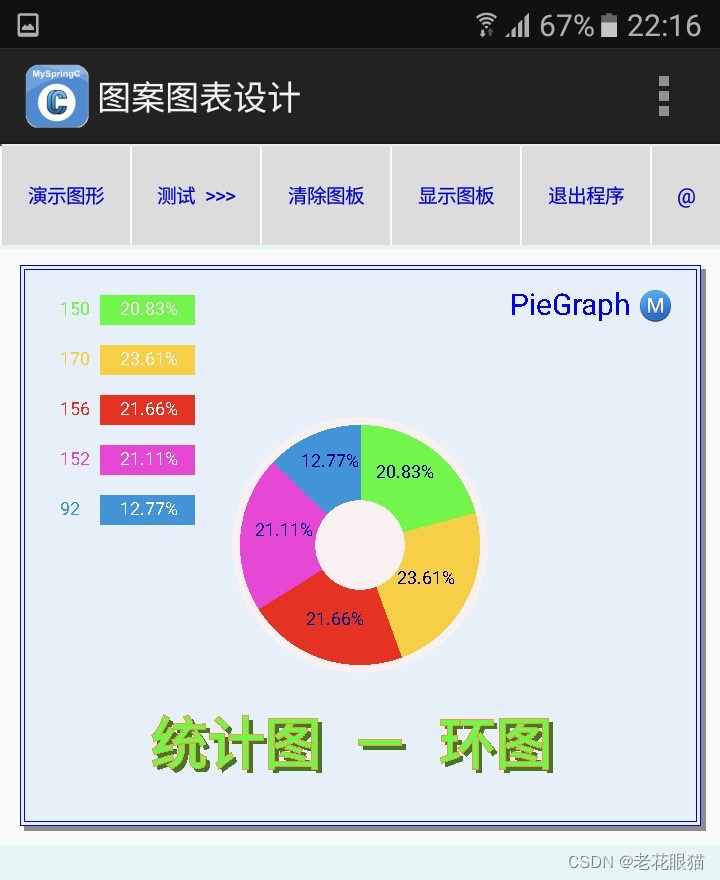
统计图饼图绘制方法(C语言)
统计图饼图绘制方法(C语言) 常用的统计图有条形图、柱形图、折线图、曲线图、饼图、环形图、扇形图。 前几类图比较容易绘制,饼图绘制较难。今值此介绍饼图的绘制方法。 本方法采用C语言的最基本功能: ( 1.)…...

洛谷C++简单题小练习day12—寻找最小值小程序
day12--寻找最小值--2.16 习题概述 题目描述 给出 n 和 n 个整数 ai,求这 n 个整数中最小值是什么。 输入格式 第一行输入一个正整数 n,表示数字个数。 第二行输入 n 个非负整数,表示 1,2…a1,a2…an,以空格隔开。 …...

相机图像质量研究(13)常见问题总结:光学结构对成像的影响--鬼影
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...
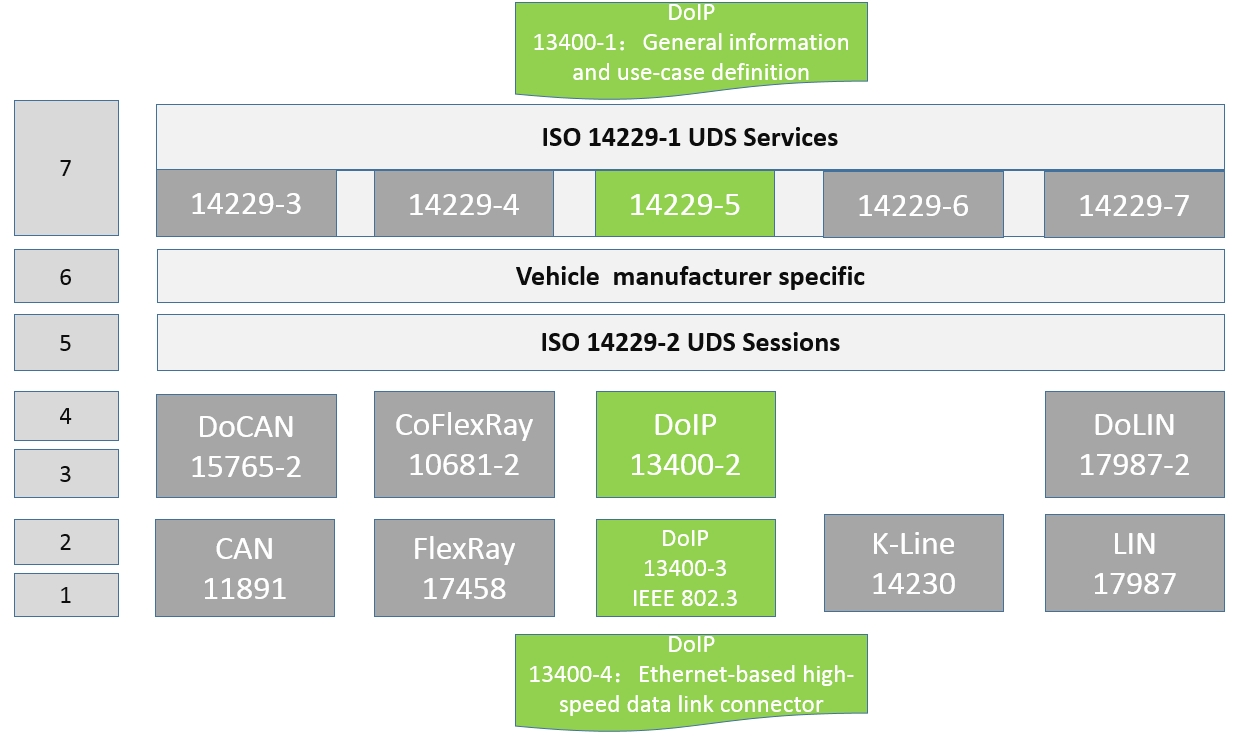
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师(Wechat:gongkenan2013)。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 本就是小人物,输了就是输了,不要在意别人怎么看自己。江湖一碗茶,…...

掘根宝典之C++包含对象的类,私有继承,保护继承,三大继承方式总结
包含对象成员的类 包含,组合和层次化:一个类里面的类成员之一是个类对象 我们来看个例子 #include<iostream> using namespace std; class AA { private:int a_; public:AA(int a):a_(a){}void A(){cout << a_ << endl;} }; class …...

第六篇:MySQL图形化管理工具
经过前五篇的学习,对于数据库这门技术的理解,我们已经在心中建立了一个城堡大致的雏形,通过命令行窗口(cmd)快速上手了【SQL语法-DDL-数据定义语言】等相关命令 道阻且长,数据库技术这一宝藏中还有数不清的…...

计算机网络——12DNS
DNS DNS的必要性 IP地址标识主机、路由器但IP地址不好记忆,不便于人类用使用(没有意义)人类一般倾向于使用一些有意义的字符串来标识Internet上的设备存在着“字符串”——IP地址的转换的必要性人类用户提供要访问机器的“字符串”名称由DN…...
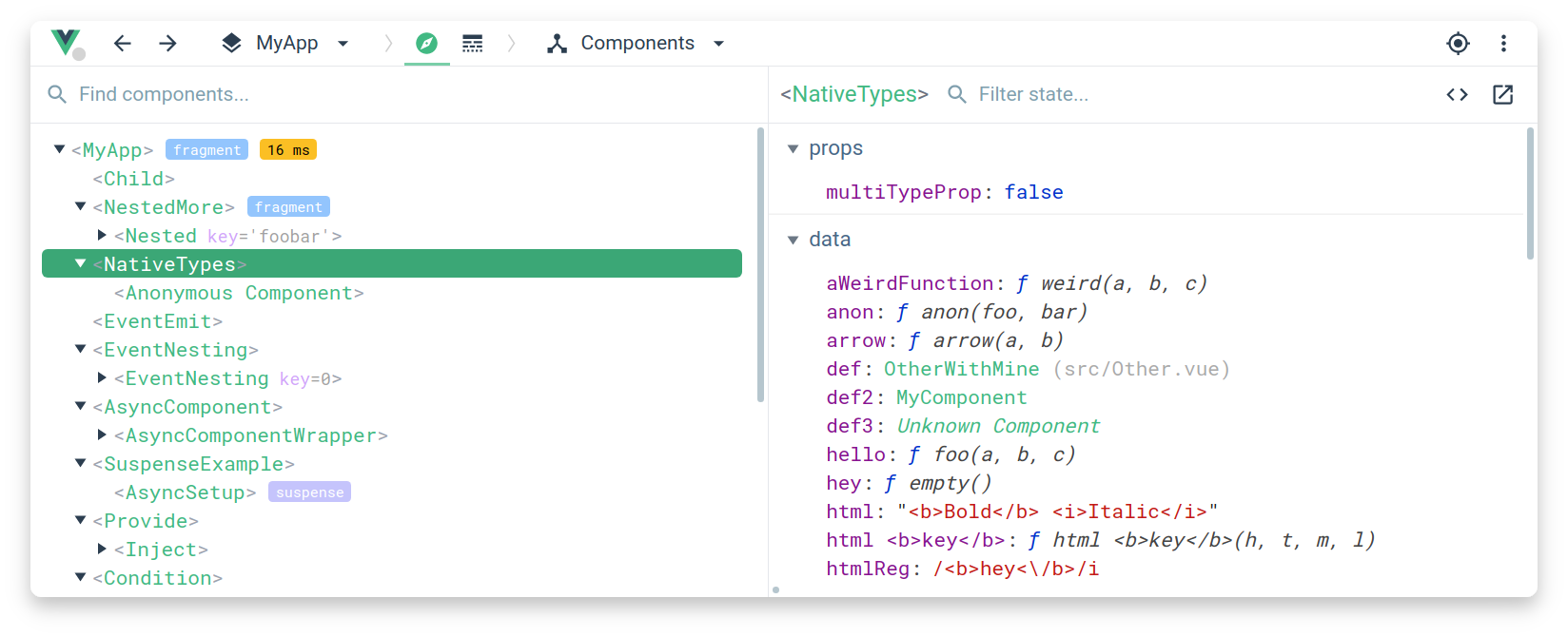
vue3-应用规模化-工具链
工具链 项目脚手架 Vite Vite 是一个轻量级的、速度极快的构建工具,对 Vue SFC 提供第一优先级支持。作者是尤雨溪,同时也是 Vue 的作者! 要使用 Vite 来创建一个 Vue 项目,非常简单: (推荐)…...
EasyExcel动态列导出
测试代码地址:https://gitee.com/wangtianwen1996/cento-practice/tree/master/src/test/java/com/xiaobai/easyexcel/dynamiccolumn 官方文档:https://easyexcel.opensource.alibaba.com/docs/2.x/quickstart/write 一、实现方式 1、根据需要导出的列…...

JAVA面试题11
什么是Java的访问修饰符,并列出它们的作用。 Java的访问修饰符包括public、private、protected和默认。它们的作用如下: public: 可以被任何其他类访问。 private: 只能被所在类访问,其他类无法访问。 protected: 可以被所在类和同一个包中的…...
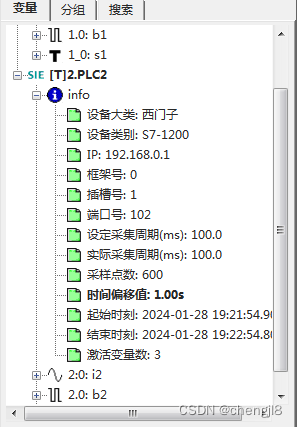
工业数据采集的时间不确定性及PLC-Recorder的通道偏移功能
目录 一、缘起 二、效果展示 三、设置方法 四、小结 一、缘起 大家都知道采集软件首先要尽可能还原数据原来的状态,给用户提供一个可以信赖的参考。但是,数据采集又有很多随机因素:Windows是一个周期不严格的系统、以太网通讯有时间波动、…...
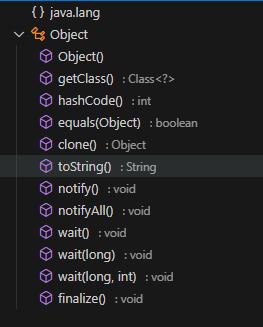
十五、Object 类
文章目录 Object 类6.1 public Object()6.2 toString方法6.3 hashCode和equals(Object)6.4 getClass方法6.5 clone方法6.6 finalize方法 Object 类 本文为书籍《Java编程的逻辑》1和《剑指Java:核心原理与应用实践》2阅读笔记 java.lang.Object类是类层次结构的根…...
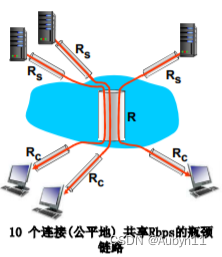
计算机网络——06分组延时、丢失和吞吐量
分组延时、丢失和吞吐量 分组丢失和延时是怎样发生的 在路由器缓冲区的分组队列 分组到达链路的速率超过了链路输出的能力分组等待排到队头、被传输 延时原因: 当当前链路有别的分组进行传输,分组没有到达队首,就会进行排队,从…...
[C#] 如何调用Python脚本程序
为什么需要C#调用python? 有以下几个原因需要C#调用Python: Python拥有丰富的生态系统:Python有很多强大的第三方库和工具,可以用于数据科学、机器学习、自然语言处理等领域。通过C#调用Python,可以利用Python的生态系…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
