数据结构-堆
1.容器
容器用于容纳元素集合,并对元素集合进行管理和维护.
传统意义上的管理和维护就是:增,删,改,查.
我们分析每种类型容器时,主要分析其增,删,改,查动作实现,及复杂度.
2.堆
2.1.结构
2.1.1.图解
堆是容器类型.
采用容器内元素在线性空间连续存储的组织方式(数组也是如此).
但除此之外,基于元素的组织方式,为其抽象出了一层二叉树的逻辑关系.
以一个具体实例来说明.
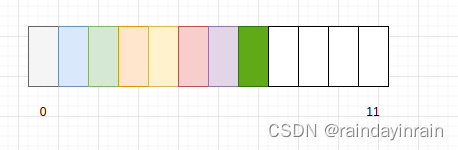
上图是代表了一个可容纳12个元素的线性空间.现在存储了8个有效元素.堆的元素存储和数组一致.
但堆为其顺序存储的元素抽象出了一层二叉树的逻辑关系.
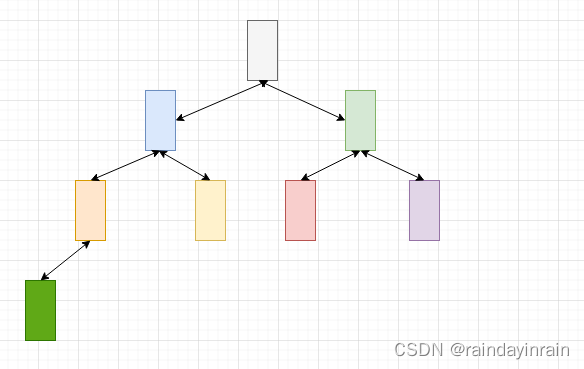
抽象的过程为,对顺序存储的每个元素,依次用这些元素顺序填满一颗满二叉树.
所谓满二叉树指的是,除了树最后一层,其余各层均是满的.最后一层,最后一个元素左边各个元素均是存在的.
如果观察特点可以得出以下结论,对顺序存储中索引为nIndex的元素.
逻辑结构里,其左孩子是索引为(2*nIndex+1)的元素,其右孩子是索引为(2*nIndex+2)的元素.
堆针对逻辑结构又施加了一层限制.
对最大堆来说,这层限制是:对堆中任一元素,该元素需要大于等于其左孩子,其右孩子上的元素.
对最小堆来说,这层限制是:对堆中任一元素,该元素需小于等于其左孩子,其右孩子上的元素.
在以上条件均满足下,可被利用的性质是:
(1). 首个元素是所有元素中最大的(对最大堆),最小的(对最小堆).
(2). 抽象出来的二叉树由于是满二叉树,其高度为:log以2为底n的对数.
2.1.2.存在一致性约束容器特点
(1). 插入无需提供位置信息.
(2). 不支持直接原地修改.一般分解为移除,添加两个过程.
(3). 由于元素值决定其位置,这类容器一般插入元素时,以std::pair<key, value>形式插入.即元素包含键,值两部分.键用来实现一致性约束.值是此键关联的实际内容.
2.2.动作
2.2.0.建堆
意思是直接给一个连续存储的元素集合,把这些元素集合调整为符合堆性质的元素集合.
最直观当然是对集合内每个元素直接执行插入,这样所有元素插入完毕,就得到一个由这些元素构成的堆.
这里介绍另一种方式.
从集合最后一个元素反向遍历到第一个元素.
对每次遍历到的元素,让其符合:以该元素为根子树中所有元素均满足堆的性质.
下面介绍针对每个遍历到元素的调节过程.
不妨假设我们现在遍历到的元素是p.假设是最小堆.
由于我们之前每次遍历时,均按上述要求.所以,p的左孩子为根子树中所有元素此时均满足堆的性质.p的右孩子为根子树也是如此.此刻子树中唯一可能不满足要求的就是p和其左,右孩子.
若p小于其左,右孩子上的元素,则无需调节.
否则,找到三者中最小元素q.交换此q和p的位置.
交换后对p和其左右孩子来说堆的性质得到满足.但对q来说,由于此位置元素变大了.所以,此刻子树中只有q与其左右孩子可能不满足堆的性质.这样,我们虽然未立即解决问题.但将问题转化为了一个同类型问题.
由于树的高度有限,每次转化后我们在更低一层子树上再次处理同类问题.
故,即使最坏下,至多经过有限次调节,也可解决问题.
2.2.1.增
堆中插入新元素.对于存在一致性约束的容器,元素插入到容器后,需经历调节过程.不需要也无法在指定位置实现插入.具体位置依赖调节过程.
插入过程可描述为:
(1). 将新元素放在数组尾后位置.
(2). 这样,此时数组对应的二叉树中,只有新节点p和其父亲q可能不满足堆的性质.
(3). 我们分析最小堆场景.比较p和q,若q中元素小于等于p,则无需调节.
(4). 若q中元素大于p,交换p,q内元素.交换后,由于q位置元素变小了.所以,q和其父节点可能不满足堆的性质.p位置元素变小了.故,以p和其左右孩子必然满足堆的性质.
这样,我们虽然未立即解决问题,但将问题转化了.由于树的高度有限,故,最坏下也能经过有限次迭代结束调节过程.
2.2.2.删
堆由于其性质,一般移除限定只能移除首个元素.我们分析移除首个元素过程.
删除首元素可描述为:
(1). 交换尾元素和首元素.递减有效元素数量.
(2). 我们分析最小堆场景.此时,首元素p相比原来变大了.此时,整棵树中只有p和其左右孩子可能不满足堆的性质.
(3). 我们寻找节点p,其左孩子lp,其右孩子rp,三者中最小元素及其位置.
(4). 若最小元素是p,则无需调节.
(5). 若最小元素是某个孩子cp(要么lp,要么rp).交换cp和p上元素.这样,交换后p和其左右孩子此时满足了堆的性质.但cp上元素变大了,所以,此时cp和其左右孩子可能不满足堆的性质.
这样,我们虽然未能立即解决问题.但将问题转化了.由于树的高度有限,故,最环下也能经过有限次迭代结束调节过程.
2.2.3.查
堆一般只提供访问首元素方法即可.
访问首元素直接基于索引访问即可.
2.2.4.改
对于存在一致性约束的容器,一般不会允许直接修改元素的值.
此类操作一般分解为:删除老元素,添加新元素两个过程来实现.
删除非首元素,类似删除首元素过程.只不过此时先交换删除位置元素和尾部元素.再从此开始进入调节流程.
2.3.时间复杂度
评价容器的依据一个是其占据的线性空间,一个是操作执行的时间复杂度.
堆的各个操作时间复杂度为:
(1). 增:Θ(log以2为底n的对数)
(2). 删:Θ(log以2为底n的对数)
(3). 查:Θ(1) (索引访问)
(4). 改:Θ(1) (log以2为底n的对数)
相关文章:

数据结构-堆
1.容器 容器用于容纳元素集合,并对元素集合进行管理和维护. 传统意义上的管理和维护就是:增,删,改,查. 我们分析每种类型容器时,主要分析其增,删,改ÿ…...

奔跑吧小恐龙(Java)
前言 Google浏览器内含了一个小彩蛋当没有网络连接时,浏览器会弹出一个小恐龙,当我们点击它时游戏就会开始进行,大家也可以玩一下试试,网址:恐龙快跑 - 霸王龙游戏. (ur1.fun) 今天我们也可以用Java来简单的实现一下这…...

Ubuntu 1804 And Above Coredump Settings
查看 coredump 是否开启 # 查询, 0 未开启, unlimited 开启 xiaoUbuntu:/var/core$ ulimit -c 0# 开启 xiaoUbuntu:/var/core$ ulimit -c unlimited查看 coredump 保存路径 默认情况下,Ubuntu 使用 apport 服务处理 coredump 文件ÿ…...

docker 2:安装
docker 2:安装 ubuntu 安装 docker sudo apt install docker.io 把当前用户放进 docker 用户组,避免每次运行 docker 命都要使用 sudo 或者 root 权限。 sudo usermod -aG docker $USERid $USER 看到用户已加入 docker 组 …...
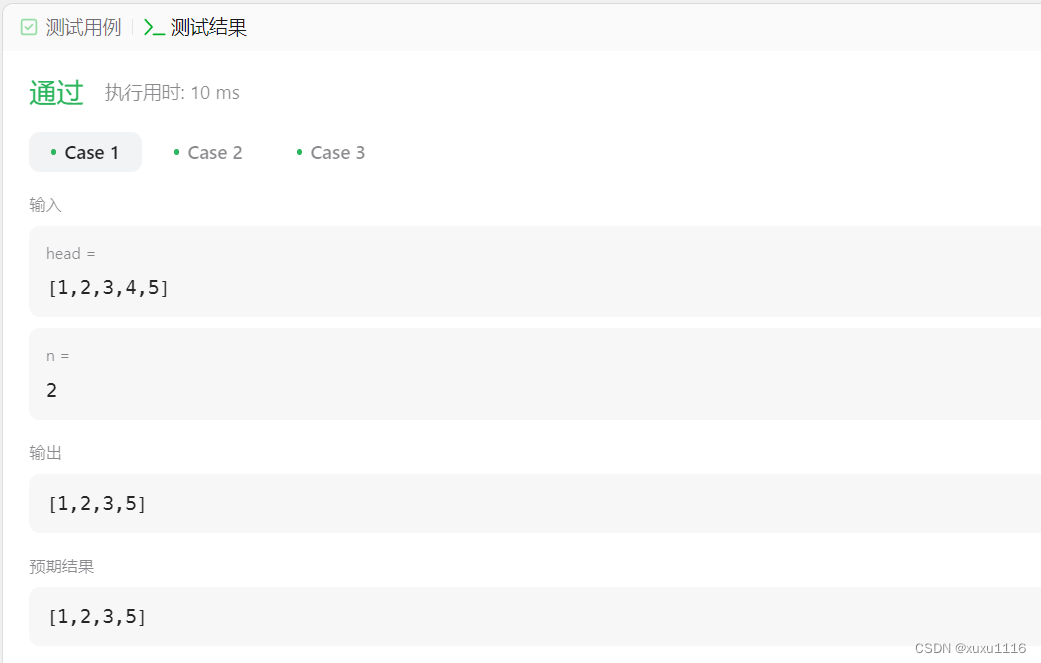
LeetCode Python - 19.删除链表的倒数第N个结点
目录 题目答案运行结果 题目 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5] 示例 2: 输入:head [1], n 1 输出&a…...
Spring Boot 笔记 005 环境搭建
1.1 创建数据库和表(略) 2.1 创建Maven工程 2.2 补齐resource文件夹和application.yml文件 2.3 porn.xml中引入web,mybatis,mysql等依赖 2.3.1 引入springboot parent 2.3.2 删除junit 依赖--不能删,删了会报错 2.3.3 引入spring web依赖…...
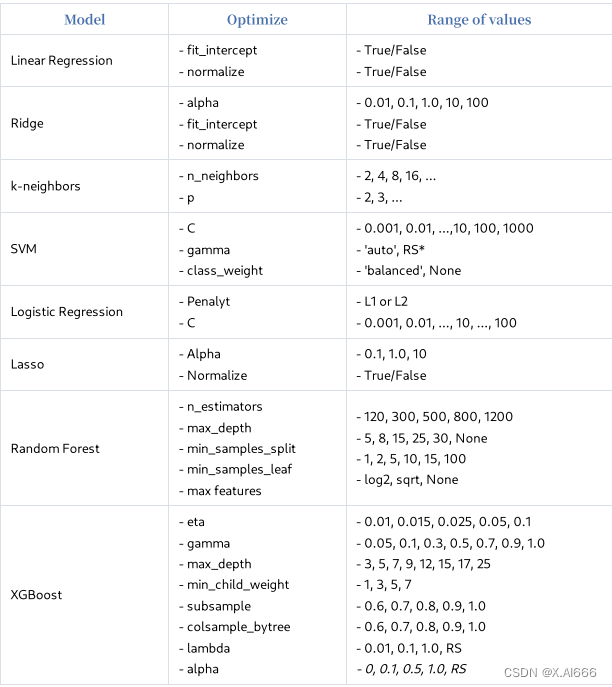
【解决(几乎)任何机器学习问题】:超参数优化篇(超详细)
这篇文章相当长,您可以添加至收藏夹,以便在后续有空时候悠闲地阅读。 有了优秀的模型,就有了优化超参数以获得最佳得分模型的难题。那么,什么是超参数优化呢?假设您的机器学习项⽬有⼀个简单的流程。有⼀个数据集&…...

面试计算机网络框架八股文十问十答第七期
面试计算机网络框架八股文十问十答第七期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)UDP协议为什么不可…...

Codeforces Round 926 (Div. 2)
A. Sasha and the Beautiful Array(模拟) 思路 最大值减去最小值 #include<iostream> #include<algorithm> using namespace std; const int N 110; int a[N];int main(){int t, n;cin>>t;while(t--){cin>>n;for(int i 0; i…...
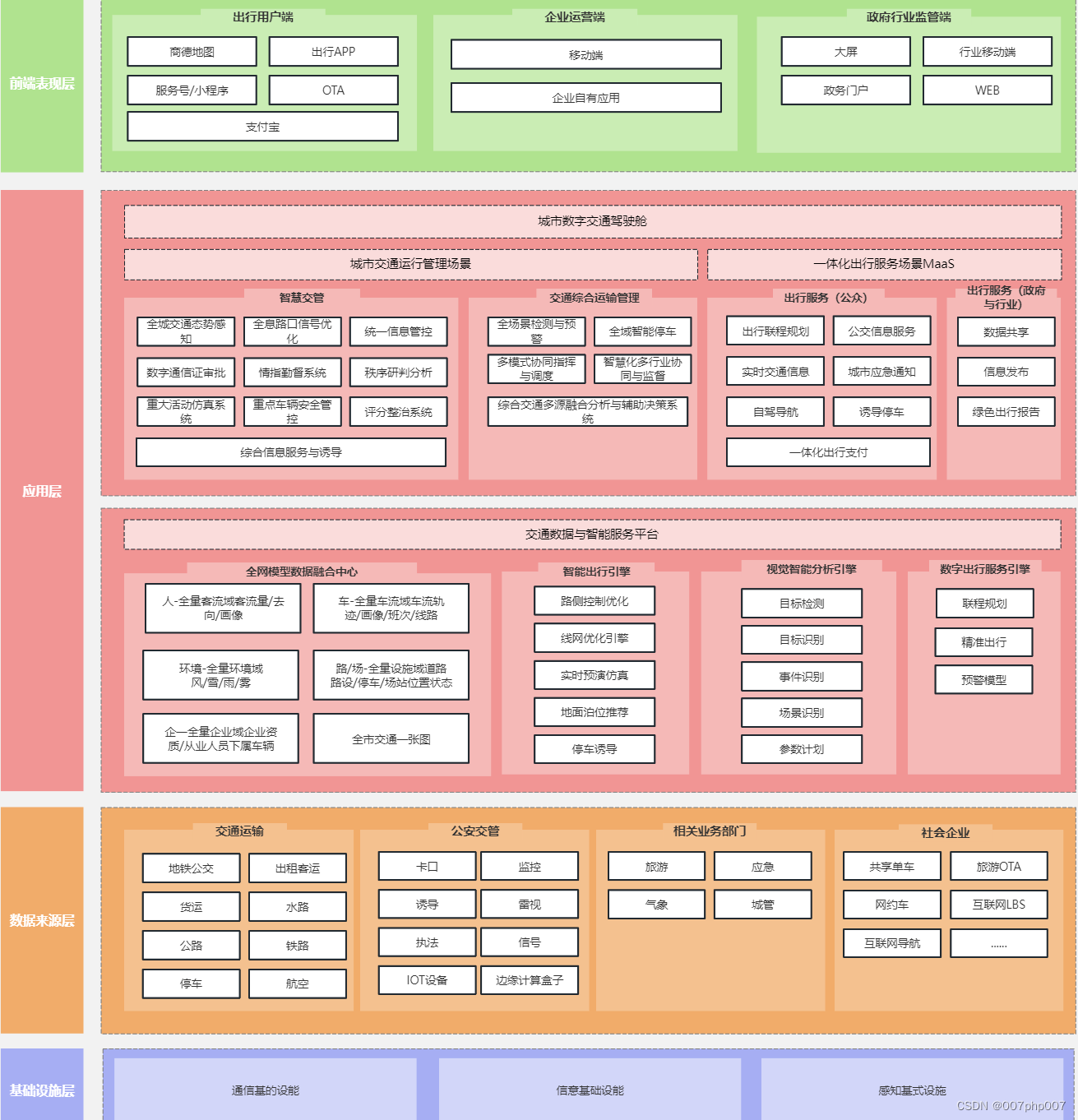
构建智慧交通平台:架构设计与实现
随着城市交通的不断发展和智能化技术的迅速进步,智慧交通平台作为提升城市交通管理效率和水平的重要手段备受关注。本文将探讨如何设计和实现智慧交通平台的系统架构,以应对日益增长的城市交通需求,并提高交通管理的智能化水平。 ### 1. 智慧…...
移动端设置position: fixed;固定定位,底部出现一条缝隙,不知原因,欢迎探讨!!!
1、问题 在父盒子中有一个子盒子,父盒子加了固定定位,需要子盒子上下都有要边距,用margin或者padding挤开时,会出现缝隙是子盒子背景颜色的。 测试过了,有些手机型号有,有些没有,微信小程序同移…...
有关网络安全的课程学习网页
1.思科网络学院 免费学习skillsforall的课程 课程链接:Introduction to Cybersecurity by Cisco: Free Online Course (skillsforall.com) 2.斯坦福大学计算机和网络安全基础 该证书对于初学者来说最有价值,它由最著名的大学之一斯坦福大学提供。您可…...

计算机网络-面试题
一、基础 1、网络编程 网络编程的本质是多台计算机之间的数据交换存在问题 如何准确的定位网络上一台或多台主机如何进行可靠传输2、网络协议 在计算机网络有序的交换数据,就必须遵守一些事先约定好的规则,比如交换数据的格式、是否需要发送一个应答信息。这些规则被称为网络…...

C++虚函数
C虚函数 在C中,虚函数(Virtual Function)是一个使用关键字virtual声明的成员函数,它在基类中被声明,以便在任何派生类中被重写(Override)。使用虚函数的目的是实现多态性——一种允许使用基类指…...
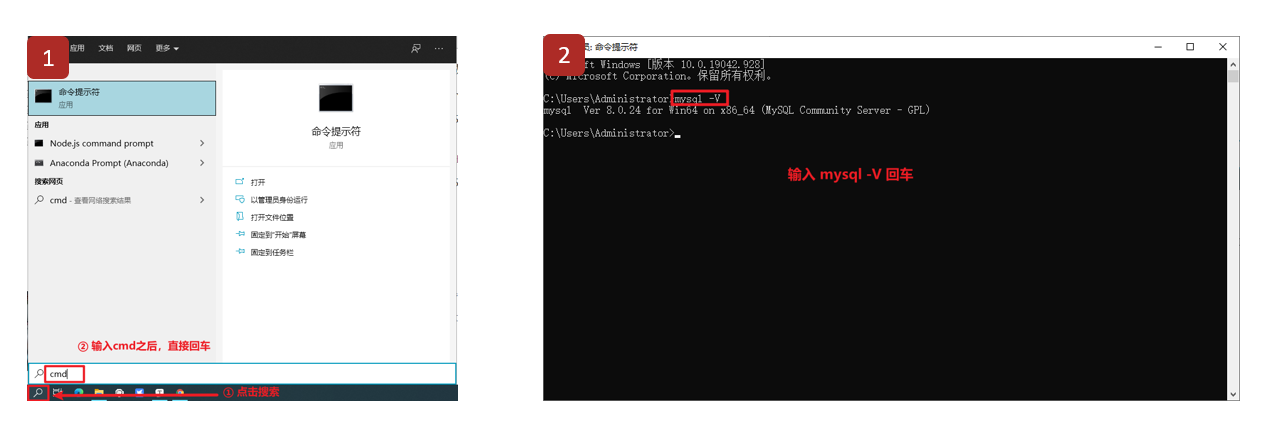
MySQL数据库基础(二):MySQL数据库介绍
文章目录 MySQL数据库介绍 一、MySQL介绍 二、MySQL的特点 三、MySQL版本 四、MySQL数据库下载与安装 1、下载 2、安装 五、添加环境变量(Windows) 六、检测环境变量是否配置成功 MySQL数据库介绍 一、MySQL介绍 MySQL是一个关系型数据库管理…...

常用文件命令
文章目录 文件命令文件内容查看catnlmoreless(more的plus版)headtailod 文件属性操作用户权限常见的权限chownchmodchgrpumask 隐藏属性常见的隐藏属性lsattrchattr 查找文件查看文件类型查找文件位置whichwhereislocatefind 文件操作(复制、…...

在屏蔽任何FRP环境下从零开始搭建安全的FRP内网穿透服务
背景 本人目前在境外某大学读博,校园网屏蔽了所有内网穿透的工具的数据包和IP访问,为了实现在家也能远程访问服务器,就不得不先开个学校VPN,再登陆。我们实验室还需要访问另一个大学的服务器,每次我都要去找另一个大学…...

OpenGL-ES 学习(1)---- AlphaBlend
AlphaBlend OpenGL-ES 混合本质上是将 2 个片元的颜色进行调和(一般是求和操作),产生一个新的颜色 OpenGL ES 混合发生在片元通过各项测试之后,准备进入帧缓冲区的片元和原有的片元按照特定比例加权计算出最终片元的颜色值,不再是新…...

Python 函数的学习笔记
Python 函数的学习笔记 0. Python 函数的概要说明1. 自定义函数示例2. 匿名函数示例3. 内置函数示例3-1. filter() 示例3-2. map() 示例3-3. reduce() 示例 4. 可变长参数*args和**kwargs示例4-1. *args(Positional Variadic Arguments)4-2. **kwargs&am…...

详解 Redis 实现数据去重
✨✨ 欢迎大家来到喔的嘛呀的博客✨✨ 🎈🎈希望这篇博客对大家能有帮助🎈🎈 目录 言 一. Redis去重原理 1. Redis Set 数据结构 2. 基于 Set 实现数据去重 3. 代码示例 4. 总结 …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...
