1 scala集合-数组
1 定长数组
定长数组,是指数组长度不可变。定义定长数组的方法有如下两种:
- 方法1:
var/val variable_name = new Array[元素类型](数组长度) // 通过制定长度定义
例如,定义一个长度为20的Int 类型数组。
scala> val a = new Array[Int](20)
val a: Array[Int] = Array(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
- 方法2:
val/var variable_name = Array(ele1, ele2, ele3, ...) // 使用元素直接定义
例如,定义一个数组元素为 1、2、3 的数组。
scala> val a = Array(1,2,3)
val a: Array[Int] = Array(1, 2, 3)
2 变长数组
变长数组的元素个数是可以增减的,我们可以添加、删除、修改元素。我们可以使用类 scala.collection.mutable.ArrayBuffer。
定义空变长数组的语法为:
val/var variable_name = ArrayBuffer[元素类型]()
例如,定义一个变长数组,初始元素为 1、2、3
scala> import scala.collection.mutable.ArrayBufferscala> val a = ArrayBuffer(1,2,3)
val a: scala.collection.mutable.ArrayBuffer[Int] = ArrayBuffer(1, 2, 3)
2.1 添加元素到变长数组
使用操作符 += 添加元素到变长数组,例如,向变长数组 a 中添加元素 4
scala> import scala.collection.mutable.ArrayBufferscala> val a = ArrayBuffer(1,2,3)
val a: scala.collection.mutable.ArrayBuffer[Int] = ArrayBuffer(1, 2, 3)scala> a+=4
val res0: scala.collection.mutable.ArrayBuffer[Int] = ArrayBuffer(1, 2, 3, 4)
2.2 添加数组到变长数组
使用操作符 ++= 可以添加一个数组到定长数组。
scala> import scala.collection.mutable.ArrayBufferscala> val a = ArrayBuffer(1,2,3,4)
val a: scala.collection.mutable.ArrayBuffer[Int] = ArrayBuffer(1, 2, 3, 4)scala> a ++= Array(5,6)
val res1: scala.collection.mutable.ArrayBuffer[Int] = ArrayBuffer(1, 2, 3, 4, 5, 6)
2.3 删除元素
使用操作符 -= 可以删除变长数组的一个元素。
scala> import scala.collection.mutable.ArrayBufferscala> val a = ArrayBuffer(1,2,3,4,5,6)
val a: scala.collection.mutable.ArrayBuffer[Int] = ArrayBuffer(1, 2, 3, 4, 5, 6)scala> a -= 4
val res2: scala.collection.mutable.ArrayBuffer[Int] = ArrayBuffer(1, 2, 3, 5, 6)
3 遍历数组
与 Java 一样,在 Scala 中,可以通过索引或 for 表达式遍历数组。
3.1 for 直接遍历
scala> val a = Array(1,2,3)
val a: Array[Int] = Array(1, 2, 3)scala> for(i <- a) println(i)
1
2
3
3.2 通过索引遍历
scala> val a = Array(1,2,3)
val a: Array[Int] = Array(1, 2, 3)
scala> for(idx <- 0 until a.length) println(a(idx))
1
2
3
相关文章:

1 scala集合-数组
1 定长数组 定长数组,是指数组长度不可变。定义定长数组的方法有如下两种: 方法1: var/val variable_name new Array[元素类型](数组长度) // 通过制定长度定义例如,定义一个长度为20的Int 类型数组。 scala> val a new …...

双场板功率GaN HEMT电容模型以精确模拟开关行为
标题:Capacitance Modeling in Dual Field-Plate Power GaN HEMT for Accurate Switching Behavior(TED.16年) 摘要 本文提出了一种基于表面电位的紧凑模型,用于模拟具有栅极和源极场板(FP)结构的AlGaN/G…...
OpenCV Mat实例详解 四
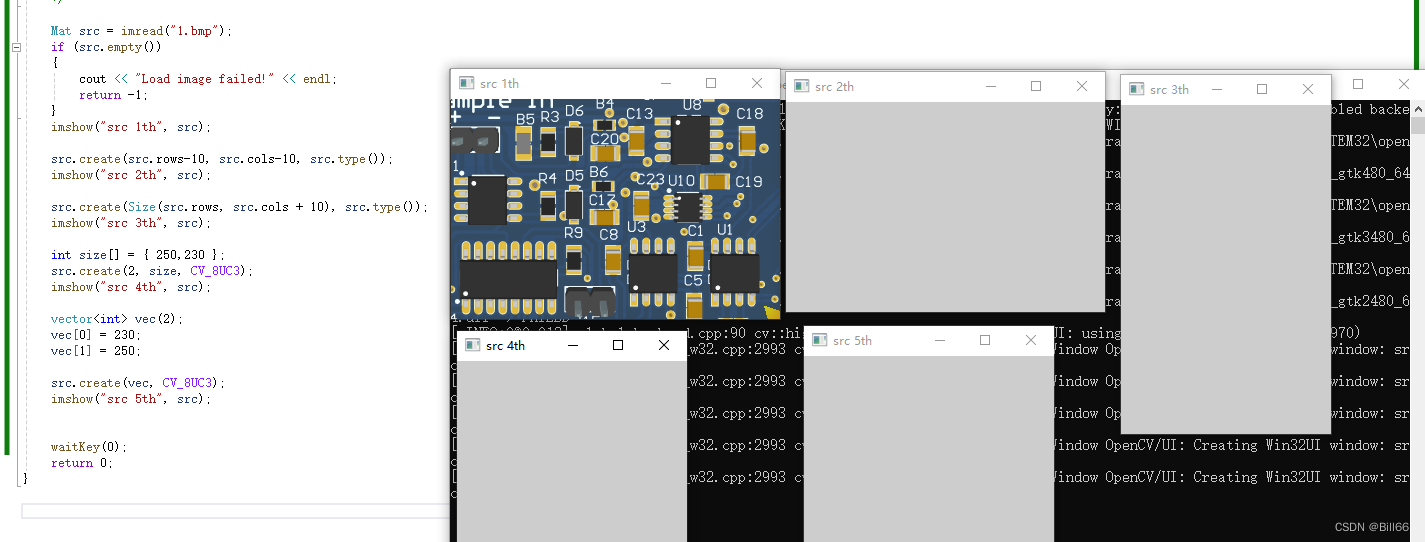
OpenCV Mat实例详解三中详细介绍来了OpenCV Mat类的公有静态成员函数,下面介绍OpenCV Mat类的其他常用成员函数。 OpenCV Mat类常用成员函数 Mat & adjustROI (int dtop, int dbottom, int dleft, int dright); dtop ROI 上边界移动值,如…...
Fluke ADPT 连接器新增对福禄克万用 Fluke 106 的支持
所需设备: 1、Fluke ADPT连接器; 2、Fluke 106; Fluke 106 拆机图: 显示界面如下图: 并且可以将波形导出到EXCEL: 福禄克万用表需要自己动手改造!!!...
算法-3-基本的数据结构
单双链表 1.单链表双链表如何反转 import java.util.ArrayList; import java.util.List;public class Code01_ReverseList {public static class Node {public int value;public Node next;public Node(int data) {value data;}}public static class DoubleNode {public int…...

探秘Java反射:灵活编程的利器
前言 大家好,我是chowley,不知道大家在学习Java的过程中有没有听过反射的概念,今天我来总结一下我心中的Java反射。 在Java编程中,反射是一种强大的工具,它允许程序在运行时检查和操作类、方法、属性等,而…...

记录 | ubuntu pyqt5 pycharm配置
Ubuntu16.04pycharmpyqt5安装与配置_ubuntu pycharm pyqt5-CSDN博客pycharm激活码 6ZUMD7WWWU-eyJsaWNlbnNlSWQiOiI2WlVNRDdXV1dVIiwibGljZW5zZWVOYW1lIjoiSmV0cyBHcm91cCIsImFzc2lnbmVlTmFtZSI6IiIsImFzc2lnbmVlRW1haWwiOiIiLCJsaWNlbnNlUmVzdHJpY3Rpb24iOiIiLCJjaGVja0NvbmN…...

ESP32学习(1)——环境搭建
使用的ESP32板子如下图所示 它可以用Arduino 软件,基于C语言开发。但是,在这里,我是用Thonny软件,基于micro_python对其进行开发。 1.安装Thonny Thonny的软件安装包,可以去它官网上下载。Thonny, Python IDE for begi…...

Attention Is All Your Need论文笔记
论文解决了什么问题? 提出了一个新的简单网络架构——transformer,仅仅是基于注意力机制,完全免去递推和卷积,使得神经网络训练地速度极大地提高。 We propose a new simple network architecture, the Transformer, based sole…...
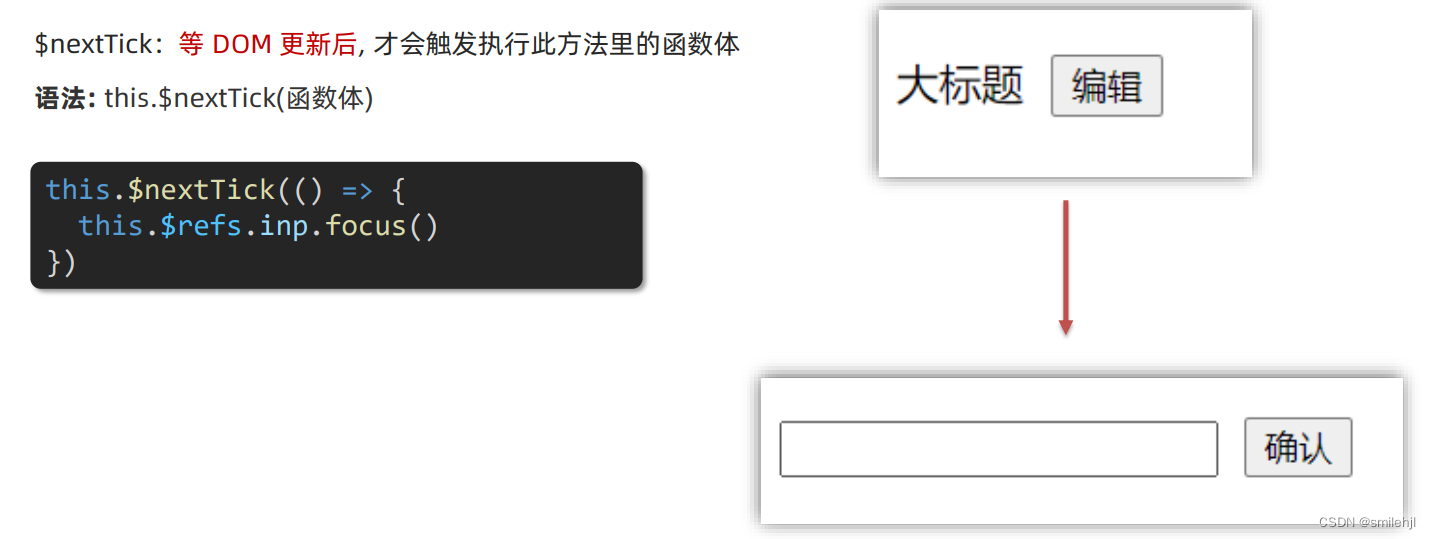
vue-进阶语法(四)
目录 v-model原理 v-model应用于组件 sync修饰符 ref 和 $refs(重点) $nextTick v-model原理 原理:v-model本质上是一个语法糖。例如应用在输入框上,就是 value属性 和 input事件 的合写。 作用:提供数据的双向…...
CGAL::2D Arrangements-7
7 几何Traits 几何Traits封装了几何实体的定义以及处理这些几何实体的几何predicates和构造的实现,供Arrangement_on_surface_2类模板和其他周边模块使用。应用于Arrangement的各种算法所确定的最小要求被组织在精细几何特征概念的层次中。每个概念列出的需求只包括…...

linux系统下vscode portable版本的rust环境搭建004:rust
目的:希望在获得一个新的系统之后,以最简便快速的方式搭配一个rust的编程环境命令在线安装只执行这句就行了 :curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh,因为是要portable安装所以按照以下的方式执行。 下载…...

从汇编角度解释线程间互斥-mutex互斥锁与lock_guard的使用
多线程并发的竞态问题 我们创建三个线程同时进行购票,代码如下 #include<iostream> #include<thread> #include<list> using namespace std; //总票数 int ticketCount100; //售票线程 void sellTicket(int idx) {while(ticketCount>0){cou…...
)
高程 | 多态性(c++)
文章目录 📚多态📚运算符重载🐇定义🐇规则🐇友元运算符重载函数🐇成员运算符重载函数 📚虚函数📚纯虚函数和抽象类 📚多态 多态:同样的消息被不同类型的对象…...
LV.23 D2 开发环境搭建及平台介绍 学习笔记
一、Keil MDK-ARM简介及安装 Keil MDK,也称MDK-ARM,Realview MDK (Microcontroller Development Kit)等。目前Keil MDK 由三家国内代理商提供技术支持和相关服务。 MDK-ARM软件为基于Cortex-M、Cortex-R4、ARM7、ARM9处理器设备…...

[uniapp生命周期]详细讲解uniapp中那些属于vue生命周期,那些属于uniapp独有的生命周期,以及这中间的区别 相关的内容和api 代码注释
目录 1. Vue.js生命周期函数2.Vue生命周期函数代码beforeCreatecreatedbeforeMountmountedbeforeUpdateupdatedbeforeDestroydestroyed$nextTick$forceUpdate$destroy 3. UniApp独有的生命周期函数onLaunchonShowonHideonError 4.总结 在UniApp中,除了Vue.js的生命周…...

【动态规划】【记忆化搜索】【状态压缩】1681. 最小不兼容性
作者推荐 【数位dp】【动态规划】【状态压缩】【推荐】1012. 至少有 1 位重复的数字 本文涉及知识点 动态规划汇总 状态压缩 记忆化搜索 1681. 最小不兼容性 给你一个整数数组 nums 和一个整数 k 。你需要将这个数组划分到 k 个相同大小的子集中,使得同一…...

JVM-类加载器 双亲委派机制
申明:文章内容是本人学习极客时间课程所写,文字和图片基本来源于课程资料,在某些地方会插入一点自己的理解,未用于商业用途,侵删。 什么是JVM JVM是Java Virtual Machine(Java虚拟机)的缩写&a…...

vue axios 请求后端无法传参问题
vue请求后端无法传参问题 问题描述处理过程总结 问题描述 在学习vue时,使用axios调用后端,发现无法把参数正确传到后端,现象如下: 使用vue发起请求,浏览器上已经有传参,但是后端没接收到对应的用户名密码&…...

打印最小公倍数
打印最小公倍数 题目描述: 输入2个整数m和n,计算m和n的最小公倍数,并打印出结果 测试1: 输入:18 24 输出:72 测试2: 输入:18 6 输出:18解法思路: 最小公倍数是指两个…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
