算法训练day29Leetcode491递增子序列46全排列47全排列Ⅱ
491 递增子序列
题目描述
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例 1:
输入:nums = [4,6,7,7] 输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
示例 2:
输入:nums = [4,4,3,2,1] 输出:[[4,4]]
提示:
1 <= nums.length <= 15-100 <= nums[i] <= 100
题目分析
而本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑!同一父节点下的同层上使用过的元素就不能再使用了
对于已经习惯写回溯的同学,看到递归函数上面的uset.insert(nums[i]);,下面却没有对应的pop之类的操作,应该很不习惯吧
这也是需要注意的点,unordered_set<int> uset; 是记录本层元素是否重复使用,新的一层uset都会重新定义(清空),所以要知道uset只负责本层!
acm模式代码
#include <iostream>
#include <vector>
#include <unordered_set>class Solution {
private:std::vector<std::vector<int>> result; // 用于存储所有递增子序列的结果集std::vector<int> path; // 用于在递归中构建当前递增子序列的路径// 回溯法主体函数void backtracking(std::vector<int>& nums, int startIndex) {// 如果路径长度大于1,将其加入结果集if (path.size() > 1) {result.push_back(path);// 注意这里不要加return,因为要取树上的所有节点}std::unordered_set<int> uset; // 使用set对本层元素进行去重for (int i = startIndex; i < nums.size(); i++) {// 如果当前元素小于路径中最后一个元素或者本层已经使用过该元素,则跳过if ((!path.empty() && nums[i] < path.back()) || uset.find(nums[i]) != uset.end()) {continue;}uset.insert(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用path.push_back(nums[i]);backtracking(nums, i + 1); // 递归调用,尝试下一个元素path.pop_back(); // 回溯,撤销上一步操作}}public:// 公有函数,调用此函数开始寻找所有递增子序列std::vector<std::vector<int>> findSubsequences(std::vector<int>& nums) {result.clear(); // 清空上一次的结果path.clear(); // 清空路径backtracking(nums, 0); // 从第一个元素开始递归return result; // 返回结果集}
};int main() {Solution solution;std::vector<int> nums = {4, 6, 7, 7}; // 示例数组auto subsequences = solution.findSubsequences(nums);std::cout << "Found " << subsequences.size() << " increasing subsequences:" << std::endl;for (const auto& seq : subsequences) {for (int num : seq) {std::cout << num << " ";}std::cout << std::endl;}return 0;
}
46 全排列
题目描述
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1] 输出:[[1]]
提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums中的所有整数 互不相同
题目分析
首先排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
acm模式代码
#include <iostream>
#include <vector>class Solution {
private:std::vector<std::vector<int>> result; // 用于存储所有可能的排列结果std::vector<int> path; // 临时存储一个排列结果// 回溯法函数void backtracking(std::vector<int> &nums, std::vector<bool>& used) {// 如果当前排列长度等于原数组长度,说明找到了一个完整的排列if (path.size() == nums.size()) {result.push_back(path); // 将当前排列加入结果集return;}for (int i = 0; i < nums.size(); i++) {// 如果数字已被使用,则跳过if (used[i] == true) {continue;}used[i] = true; // 标记数字为已使用path.push_back(nums[i]); // 将数字添加到当前排列路径中backtracking(nums, used); // 继续递归填充下一个数字path.pop_back(); // 回溯,从当前排列中移除最后一个数字used[i] = false; // 重置当前数字的使用状态}return;}
public:// 主函数,返回给定数组的所有排列组合std::vector<std::vector<int>> permute(std::vector<int>& nums) {std::vector<bool> used(nums.size(), false); // 初始化所有数字未被使用result.clear(); // 清空结果集path.clear(); // 清空当前路径backtracking(nums, used); // 开始回溯搜索return result; // 返回所有排列组合的结果集}
};int main() {Solution sol;std::vector<int> nums = {1, 2, 3}; // 示例数组std::vector<std::vector<int>> result = sol.permute(nums); // 获取所有排列// 打印所有排列for (const auto &path : result) {for (const int num : path) {std::cout << num << " ";}std::cout << std::endl;}return 0;
}
输出
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
47全排列Ⅱ
题目描述
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2],[1,2,1],[2,1,1]]
示例 2:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
1 <= nums.length <= 8-10 <= nums[i] <= 10
题目分析
去重最为关键的代码为:
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;
}对于排列问题,树层上去重和树枝上去重,都是可以的,但是树层上去重效率更高!
acm模式代码
#include <iostream>
#include <vector>
#include <algorithm> // 引入算法头文件用于排序class Solution {
private:std::vector<std::vector<int>> result; // 存储最终的排列结果std::vector<int> path; // 临时存储当前排列的路径// 回溯法函数,用于递归生成排列void backtracking(std::vector<int> &nums, std::vector<bool>& used) {// 如果当前路径长度等于原数组长度,说明找到了一个完整排列if (path.size() == nums.size()) {result.push_back(path); // 将当前路径添加到结果集中return; // 回溯}for (int i = 0; i < nums.size(); i++) {// 跳过已使用的元素或同一层级中的重复元素if (used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i -1])) {continue;}used[i] = true; // 标记当前元素为已使用path.push_back(nums[i]); // 将当前元素添加到路径中backtracking(nums, used); // 递归调用继续构建路径path.pop_back(); // 回溯,移除路径中的最后一个元素used[i] = false; // 重置当前元素为未使用}}
public:// 公共接口,返回给定数组的所有独特排列std::vector<std::vector<int>> permuteUnique(std::vector<int>& nums) {std::sort(nums.begin(), nums.end()); // 对数组进行排序,以便有效地跳过重复元素std::vector<bool> used(nums.size(), false); // 初始化使用标记数组result.clear(); // 清空结果集path.clear(); // 清空当前路径backtracking(nums, used); // 开始回溯搜索return result; // 返回结果集}
};int main() {Solution sol;std::vector<int> nums = {1, 1, 2, 3}; // 示例输入std::vector<std::vector<int>> result = sol.permuteUnique(nums); // 获取所有独特的排列// 打印所有排列for (const auto &path : result) {for (const int num : path) {std::cout << num << " ";}std::cout << std::endl;}return 0;
}
输出
1 1 2 3
1 1 3 2
1 2 1 3
1 2 3 1
1 3 1 2
1 3 2 1
2 1 1 3
2 1 3 1
2 3 1 1
3 1 1 2
3 1 2 1
3 2 1 1
相关文章:

算法训练day29Leetcode491递增子序列46全排列47全排列Ⅱ
491 递增子序列 题目描述 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。 数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一…...

内网穿透与搭建私人服务器
前言 内网穿透是一种技术,允许用户从外部网络访问内部私有网络中的服务器或设备。这对于想要从任何地方访问家中或办公室内部网络资源的用户非常有用。以下是为初学者准备的关于如何实现内网穿透以及搭建自己的私人服务器的详细指南。 在这个数字化时代,…...

交大论文下载器
原作者地址: https://github.com/olixu/SJTU_Thesis_Crawler 问题: http://thesis.lib.sjtu.edu.cn/的学位论文下载系统,该版权保护系统用起来很不方便,加载起来非常慢,所以该下载器实现将网页上的每一页的图片合并…...
)
全栈笔记_浏览器扩展篇(manifest.json文件介绍)
manifest.json介绍 是web扩展技术必不可少的插件配置文件,放在根目录作用: 指定插件的基本信息 name:名称manifest_version:manifest.json文件的版本号,可以写2或3version:版本description:描述定义插件的行为: browser_action:添加一个操作按钮到浏览器工具栏,点击按…...
)
蓝桥杯每日一题(python)
##斐波那契数列的应用 --- 题目斐波那契 题目: 如果数组 A (a0, a1, , an−1) 满足以下条件,就说它是一个斐波那契数组: 1. n ≥ 2; 2. a0 a1; 3. 对于所有的 i(i ≥ 2),都满足 ai ai−1 ai−2…...

【Vue】工程化开发脚手架Vue CLI
📝个人主页:五敷有你 🔥系列专栏:Vue⛺️稳重求进,晒太阳 工程化开发&脚手架Vue CLI 基本介绍 Vue Cli是Vue官方提供的一个全局命令工具 可以帮助我们快速创建一个开发Vue项目的标准化基础架子【集成了we…...

嵌入式培训机构四个月实训课程笔记(完整版)-Linux ARM驱动编程第三天-ARM Linux ADC和触摸屏开发 (物联技术666)
链接:https://pan.baidu.com/s/1V0E9IHSoLbpiWJsncmFgdA?pwd1688 提取码:1688 教学内容: 1、ADC S3C2440的A/D转换器包含一个8通道的模拟输入转换器,可以将模拟输入信号转换成10位数字编码。 在A/D转换时钟频率为2.5MHz时&…...
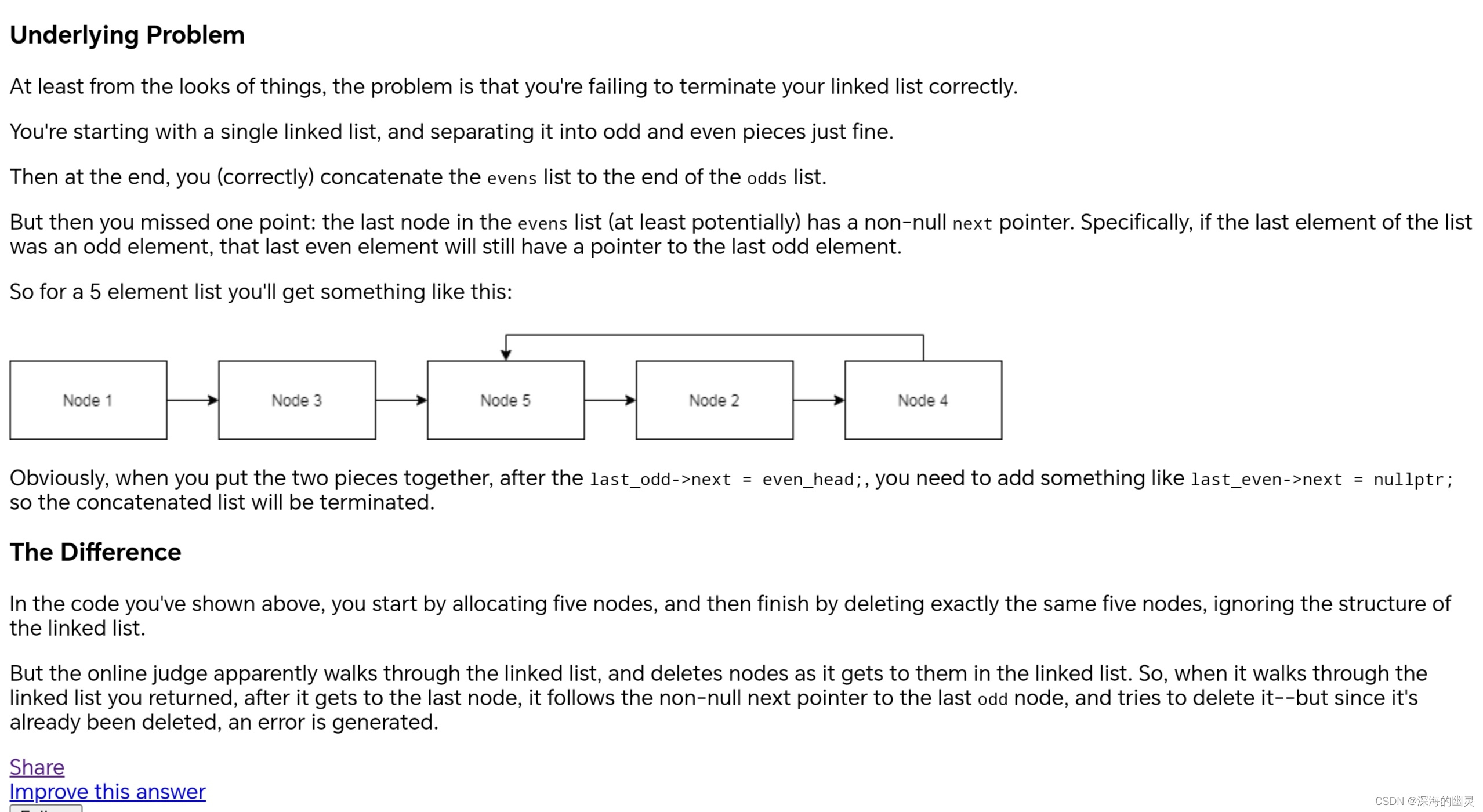
LeetCode “AddressSanitizer:heat-use-after-free on address“问题解决方法
heat-use-after-free : 访问堆上已经被释放的内存地址 现象:同样代码在LeetCode上报错,但是自己在IDE手动打印并不会报错 个人猜测,这个bug可能来源于LeetCode后台输出打印链表的代码逻辑问题。 问题描述 题目来自LeetCode的8…...

幸运彩票
L1-6 幸运彩票 分数 15 作者 陈越 单位 浙江大学 彩票的号码有 6 位数字,若一张彩票的前 3 位上的数之和等于后 3 位上的数之和,则称这张彩票是幸运的。本题就请你判断…...

搭建yum仓库服务器
安装 1.安装linux 1.1安装依赖 yum -y install gcc zlib zlib-devel pcre-devel openssl openssl-devel 1.2下载 cd /opt/nginx wget http://nginx.org/download/nginx-1.25.3.tar.gz 1.3解压 tar -xvf nginx-1.25.3.tar.gz 1.4配置 cd nginx-1.25.3 ./configure --pre…...

贪心算法练习day1
练习1--翻硬币 1)题目及要求 2)解题思路 输入的是字符串,要想将两组字符串进行一一对比,需要将字符串转换成字符数组,再使用for循环依次遍历字符数组,进行比对。 输入两行字符串,转换成两个字…...
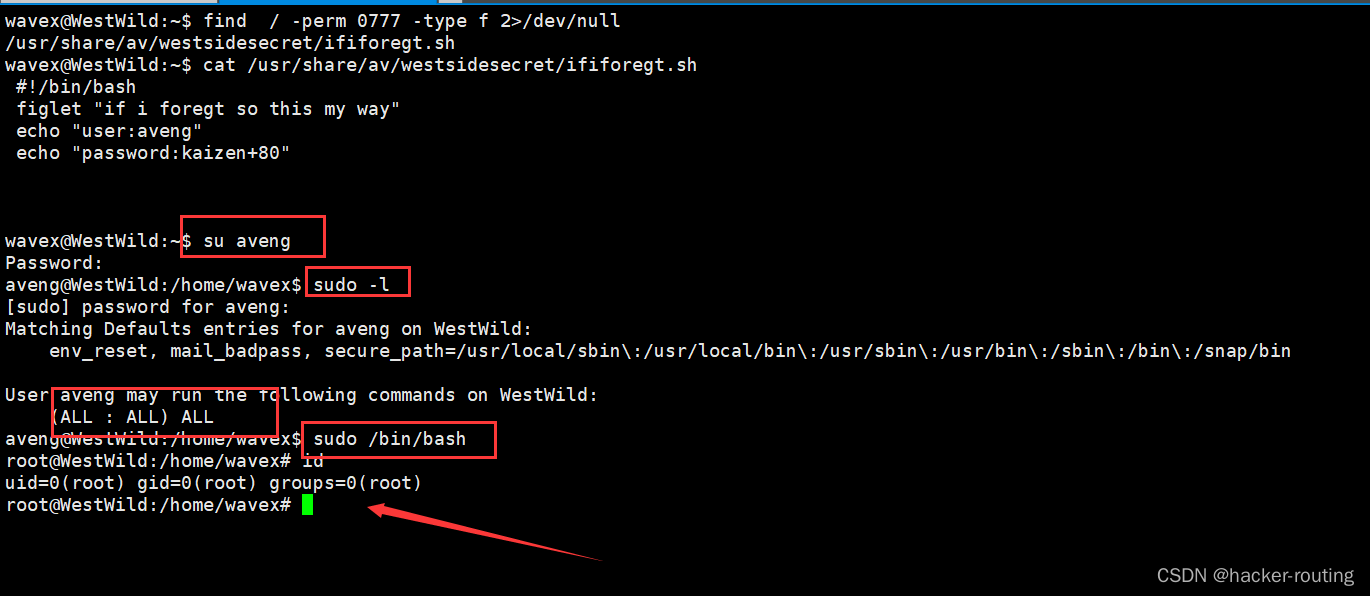
[VulnHub靶机渗透] WestWild 1.1
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【python】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏…...

如何使用 ControlValueAccessor 在 Angular 中创建自定义表单控件
简介 在 Angular 中创建表单时,有时您希望拥有一个不是标准文本输入、选择或复选框的输入。通过实现 ControlValueAccessor 接口并将组件注册为 NG_VALUE_ACCESSOR,您可以将自定义表单控件无缝地集成到模板驱动或响应式表单中,就像它是一个原…...
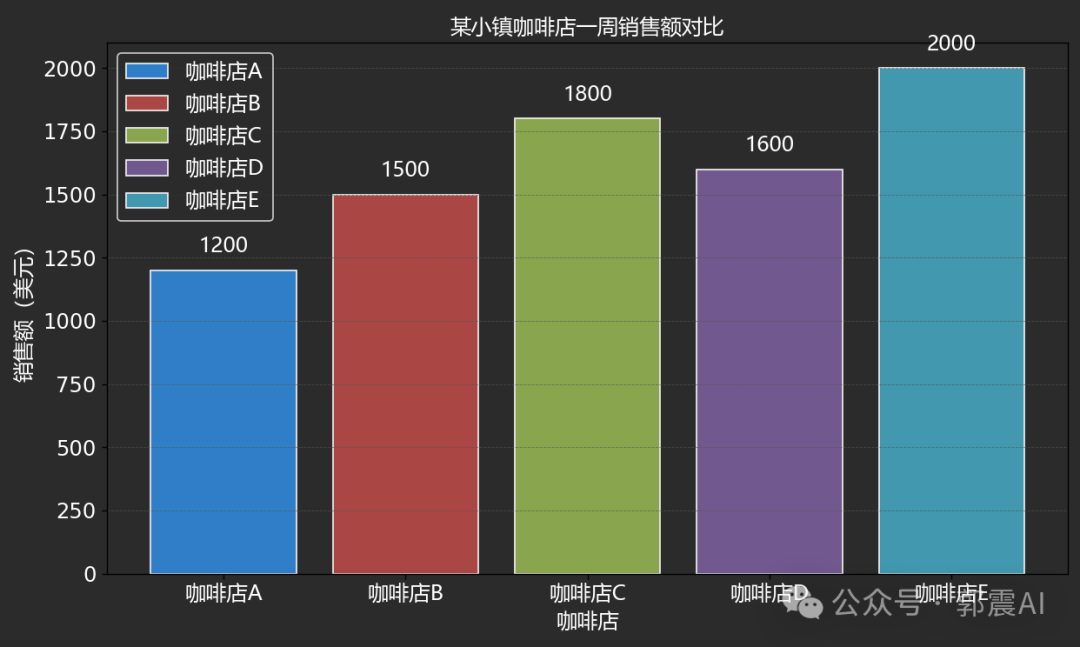
视频讲解:优化柱状图
你好,我是郭震 AI数据可视化 第三集:美化柱状图,完整视频如下所示: 美化后效果前后对比,前: 后: 附完整案例源码: util.py文件 import platformdef get_os():os_name platform.syst…...

OpenAI宣布ChatGPT新增记忆功能;谷歌AI助理Gemini应用登陆多地区
🦉 AI新闻 🚀 OpenAI宣布ChatGPT新增记忆功能,可以自由控制内存,提供个性化聊天和长期追踪服务 摘要:ChatGPT新增的记忆功能可以帮助AI模型记住用户的提问内容,并且可以自由控制其内存。这意味着用户不必…...

Solidworks:平面草图练习
继续练习平面草图,感觉基本入门了。...
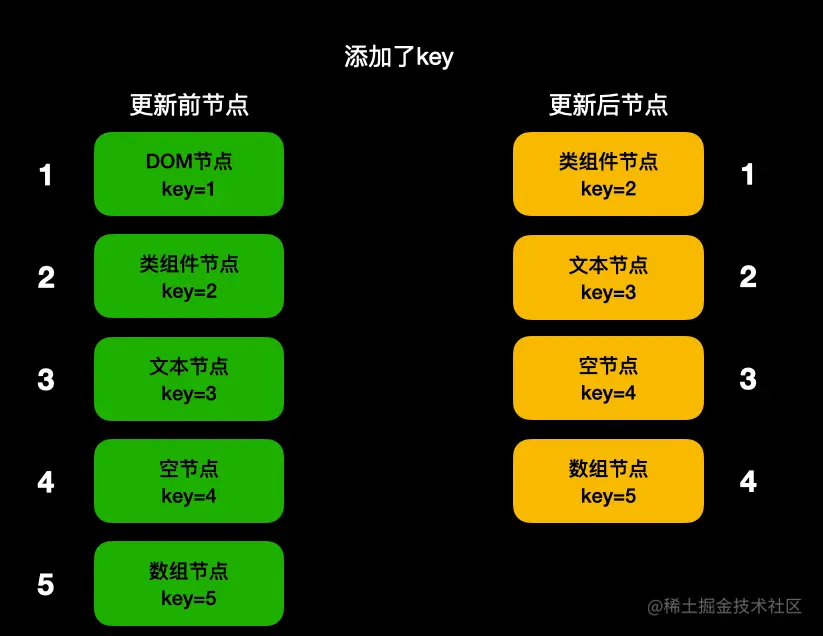
React18原理: 渲染与更新时的重点关注事项
概述 react 在渲染过程中要做很多事情,所以不可能直接通过初始元素直接渲染还需要一个东西,就是虚拟节点,暂不涉及React Fiber的概念,将vDom树和Fiber 树统称为虚拟节点有了初始元素后,React 就会根据初始元素和其他可…...
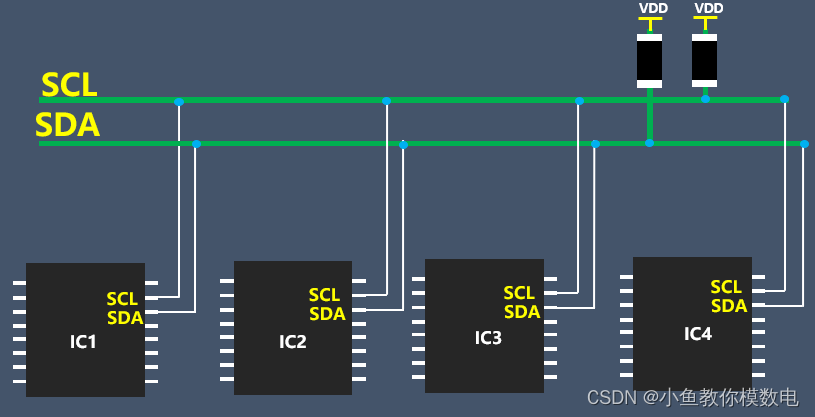
嵌入式I2C 信号线为何加上拉电阻(图文并茂)
IIC 是一个两线串行通信总线,包含一个 SCL 信号和 SDA 信号,SCL 是时钟信号,从主设备发出,SDA 是数据信号,是一个双向的,设备发送数据和接收数据都是通过 SDA 信号。 在设计 IIC 信号电路的时候我们会在 SC…...
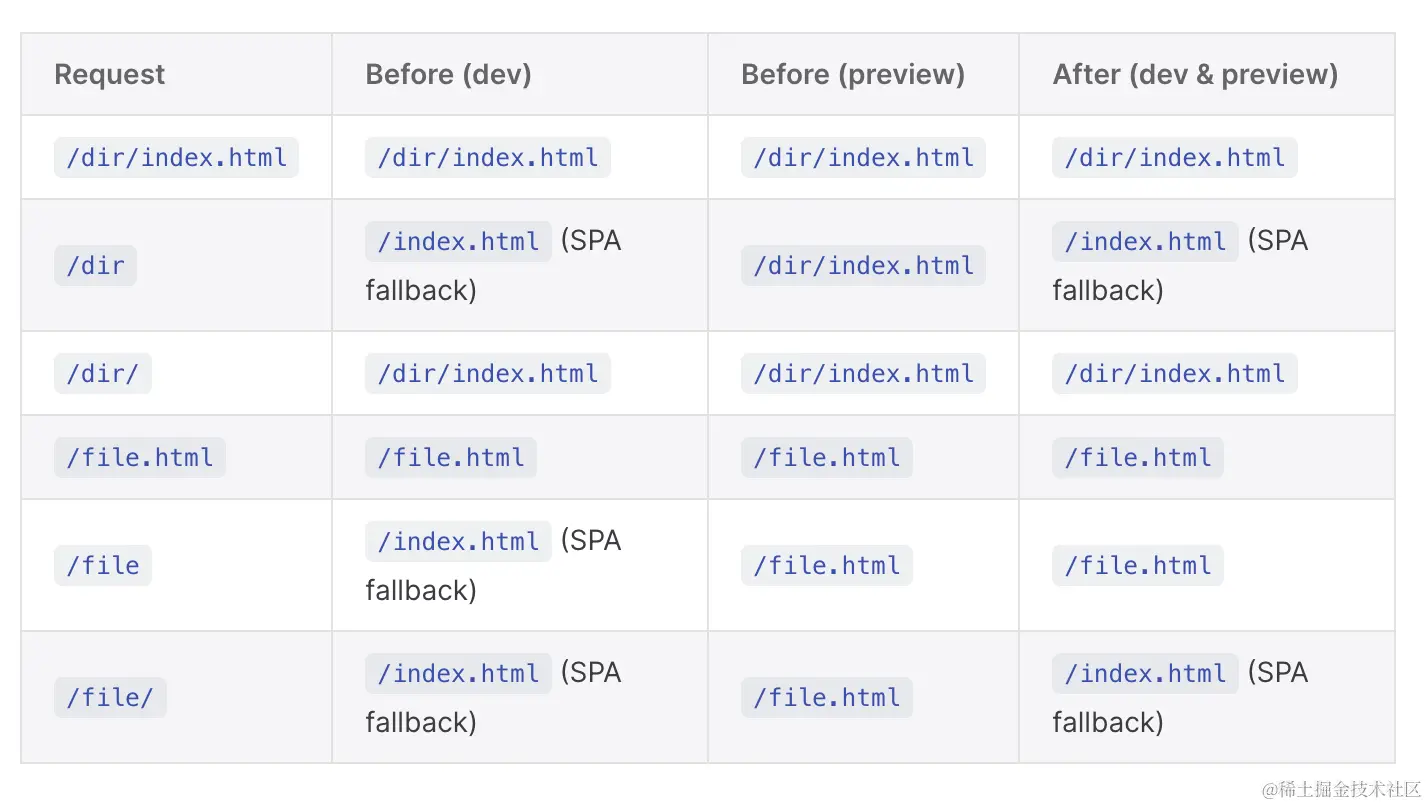
Vite 5.0 正式发布
11 月 16 日,Vite 5.0 正式发布,这是 Vite 道路上的又一个重要里程碑!Vite 现在使用 Rollup 4,这已经代表了构建性能的大幅提升。此外,还有一些新的选项可以改善开发服务器性能。 Vite 4 发布于近一年前,它…...
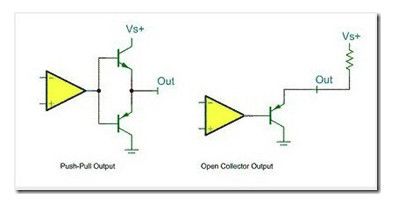
嵌入式STM32 单片机 GPIO 的工作原理详解
STM32的 GPIO 介绍 GPIO 是通用输入/输出端口的简称,是 STM32 可控制的引脚。GPIO 的引脚与外部硬件设备连接,可实现与外部通讯、控制外部硬件或者采集外部硬件数据的功能。 以 STM32F103ZET6 芯片为例子,该芯片共有 144 脚芯片,…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
