代码随想录算法训练营第31天|● 理论基础 ● 455.分发饼干 ● 376. 摆动序列 ● 53. 最大子序和
文章目录
- 理论基础
- 分发饼干
- 思路:
- 代码:
- 摆动序列
- 思路一 贪心算法:
- 代码:
- 思路二:动态规划(想不清楚)
- 代码:
- 最大子序和
- 思路:
- 代码:
理论基础
贪心算法其实就是没有什么规律可言,所以大家了解贪心算法 就了解它没有规律的本质就够了。
不用花心思去研究其规律, 没有思路就立刻看题解。
基本贪心的题目 有两个极端,要不就是特简单,要不就是死活想不出来。
学完贪心之后再去看动态规划,就会了解贪心和动规的区别
分发饼干
添加链接描述

思路:
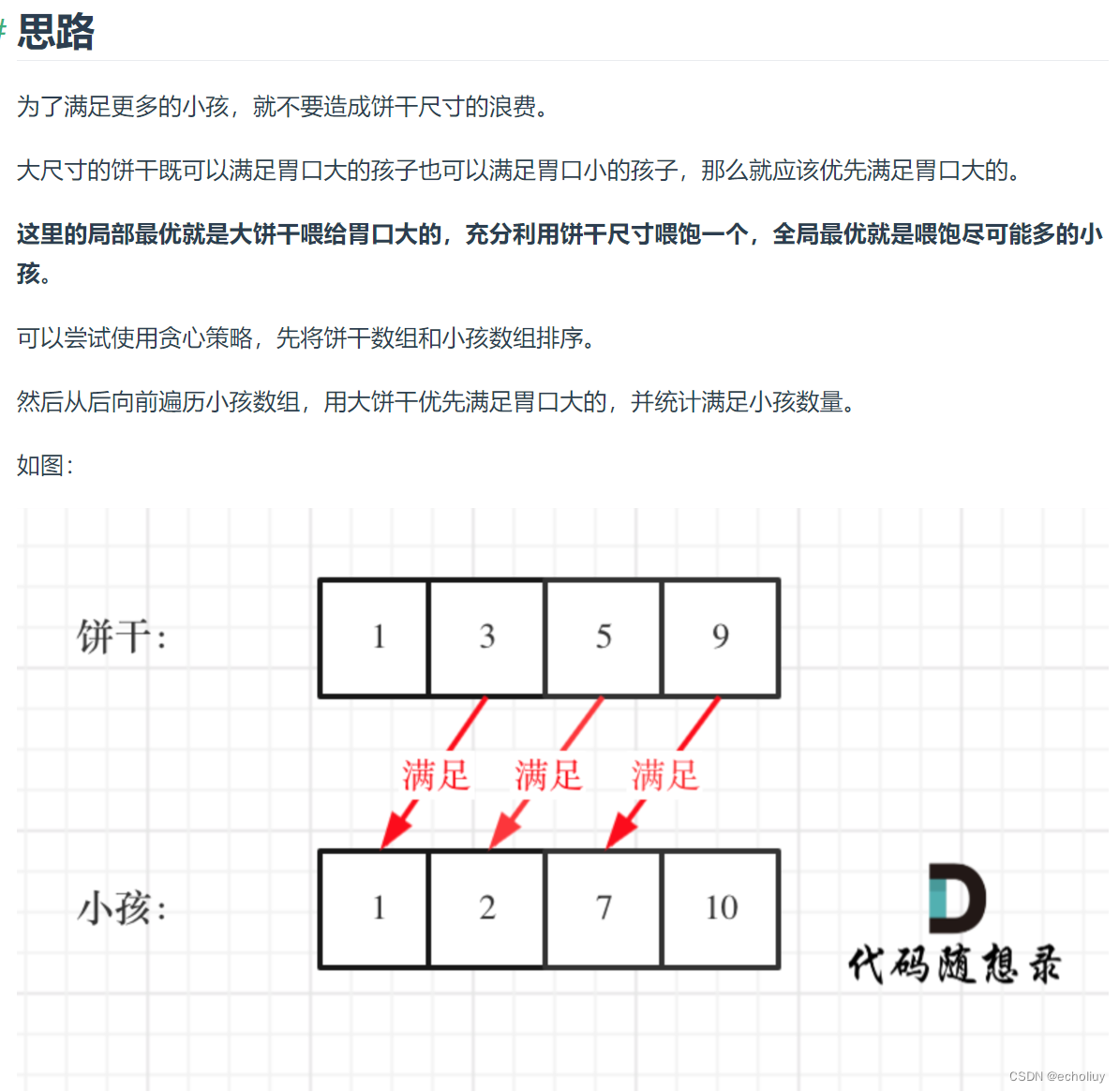
从代码中可以看出我用了一个 index 来控制饼干数组的遍历,遍历饼干并没有再起一个 for 循环,而是采用自减的方式,这也是常用的技巧。
有的同学看到要遍历两个数组,就想到用两个 for 循环,那样逻辑其实就复杂了。
代码:
class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int start = s.length-1;//饼干的下标int res=0;for(int i=g.length-1;i>=0;i--){// 循环判断if(start>=0&&s[start]>=g[i]){res++;start--;}}return res;}
}
摆动序列

思路一 贪心算法:
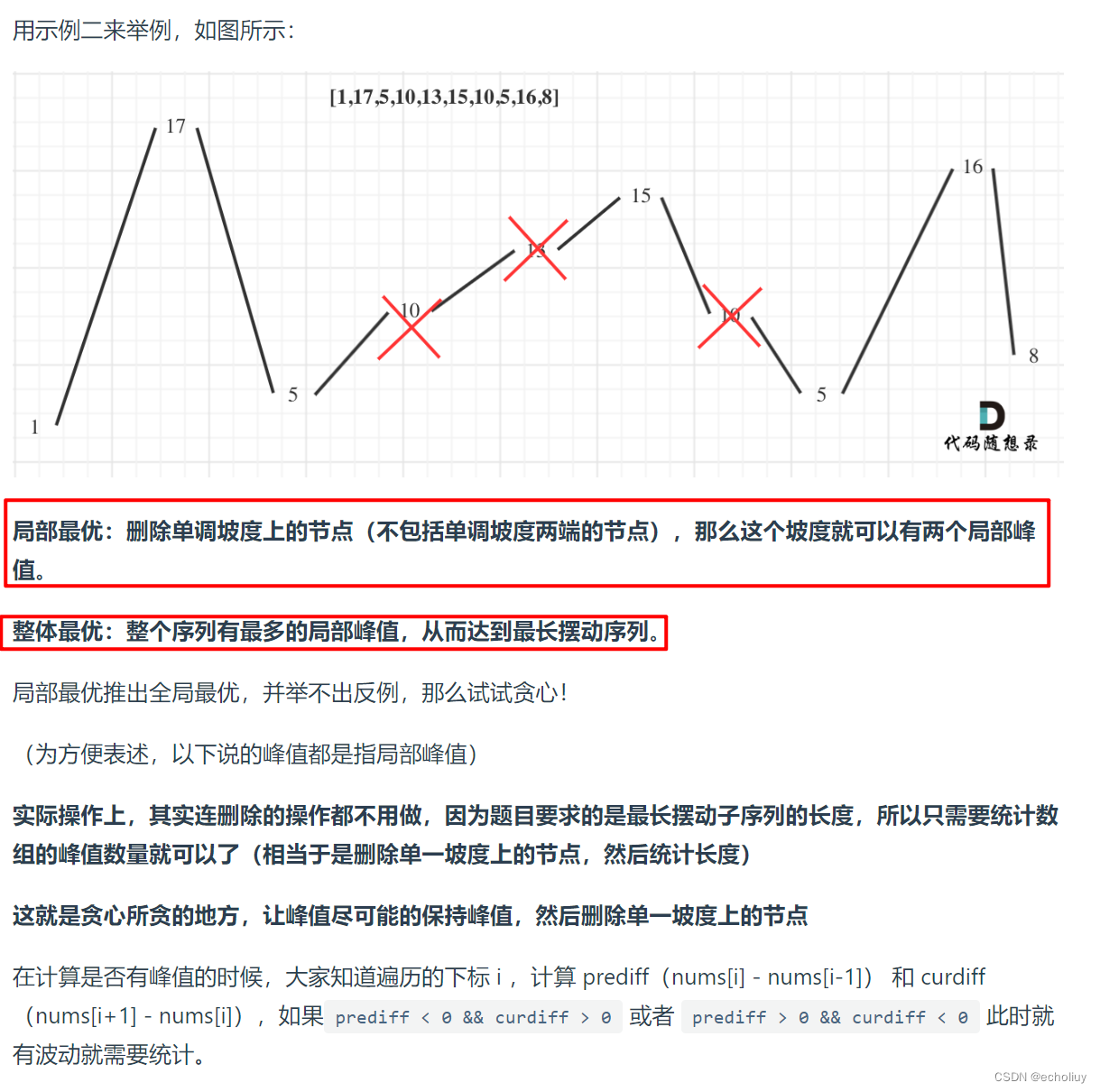
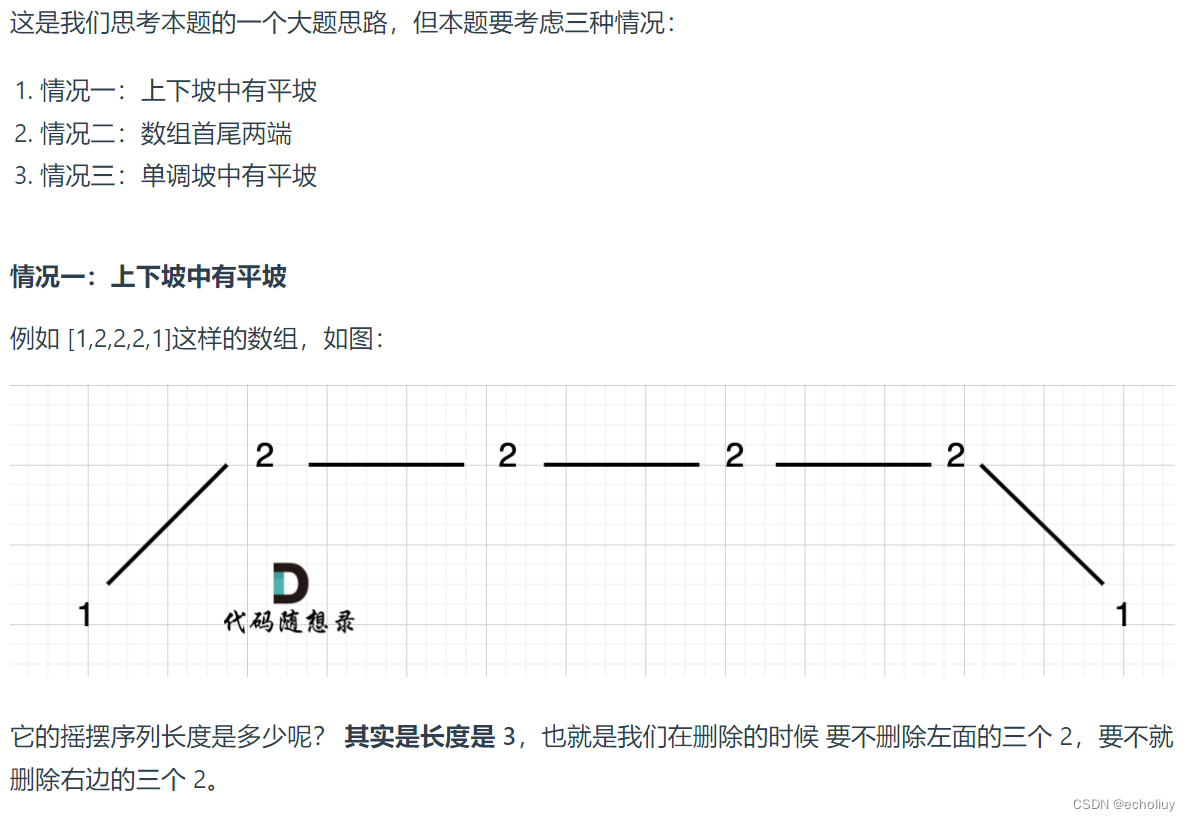
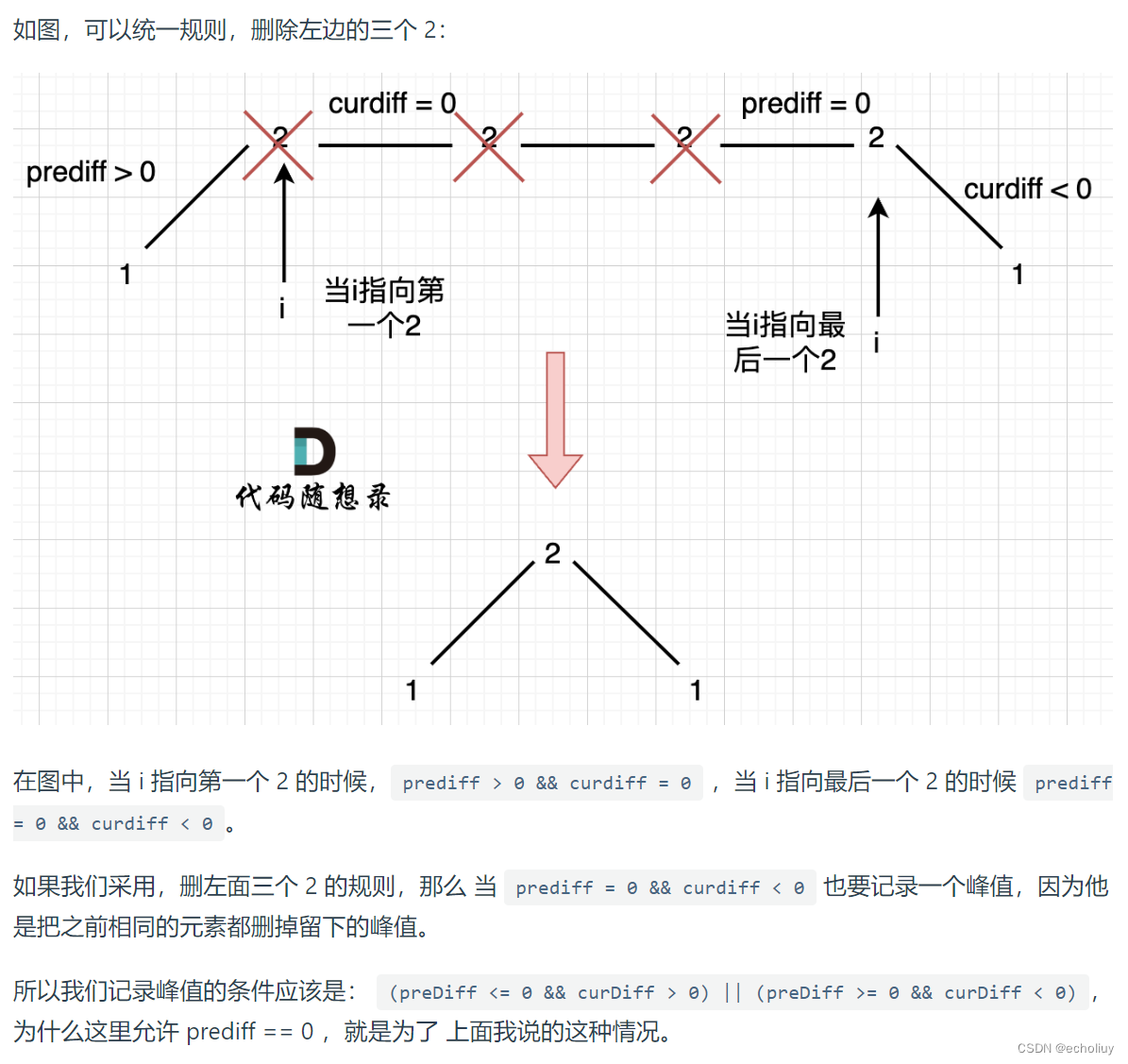

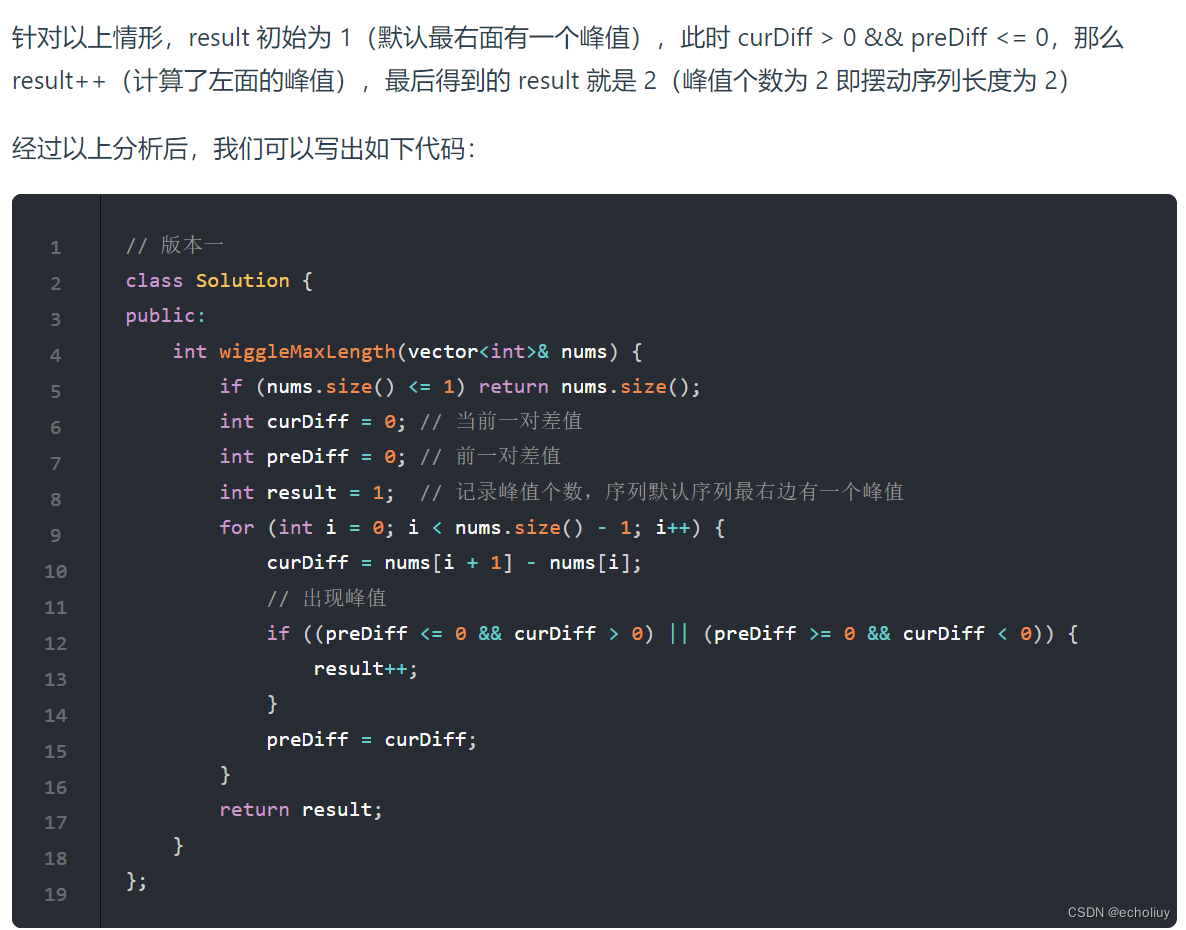
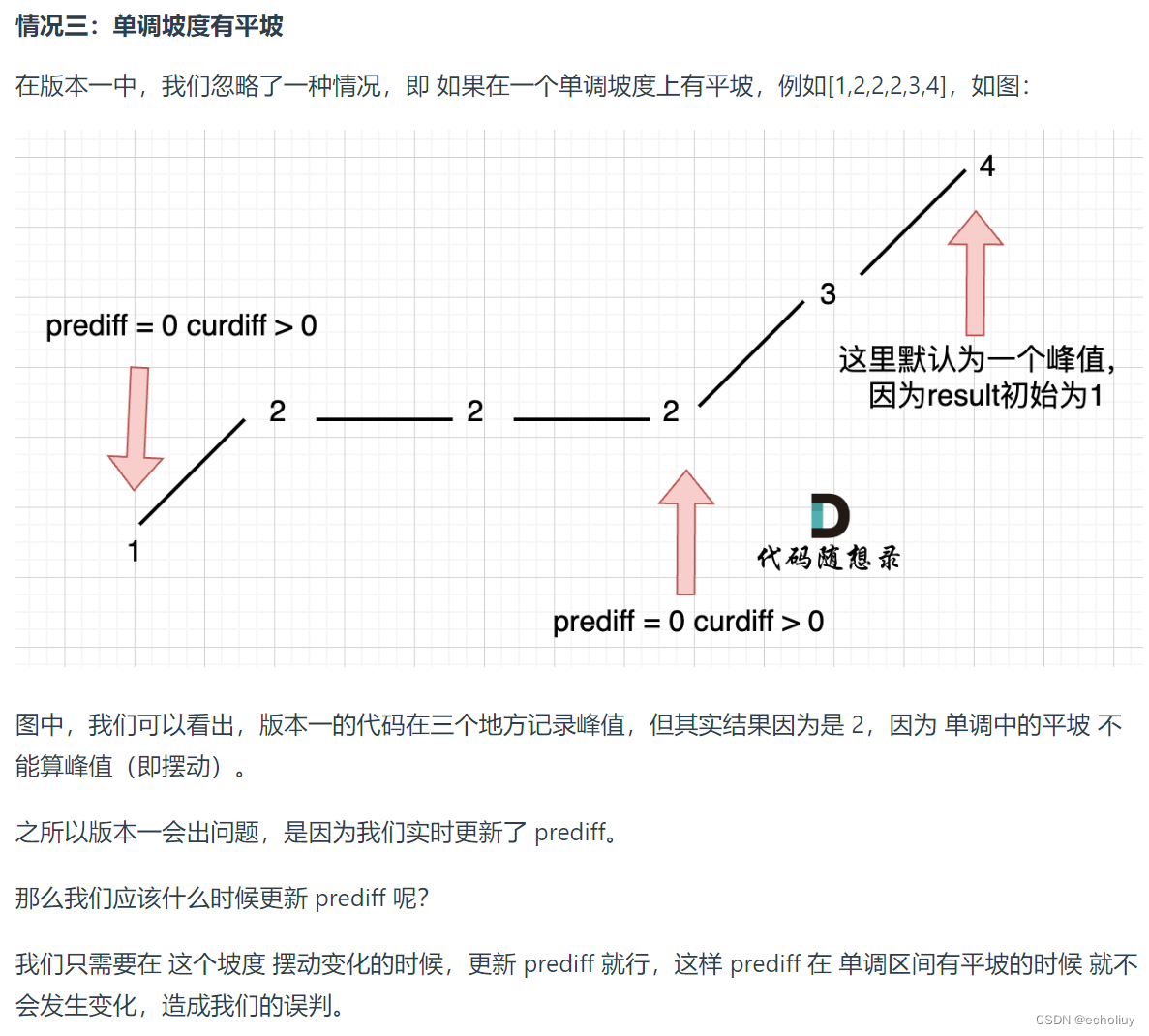
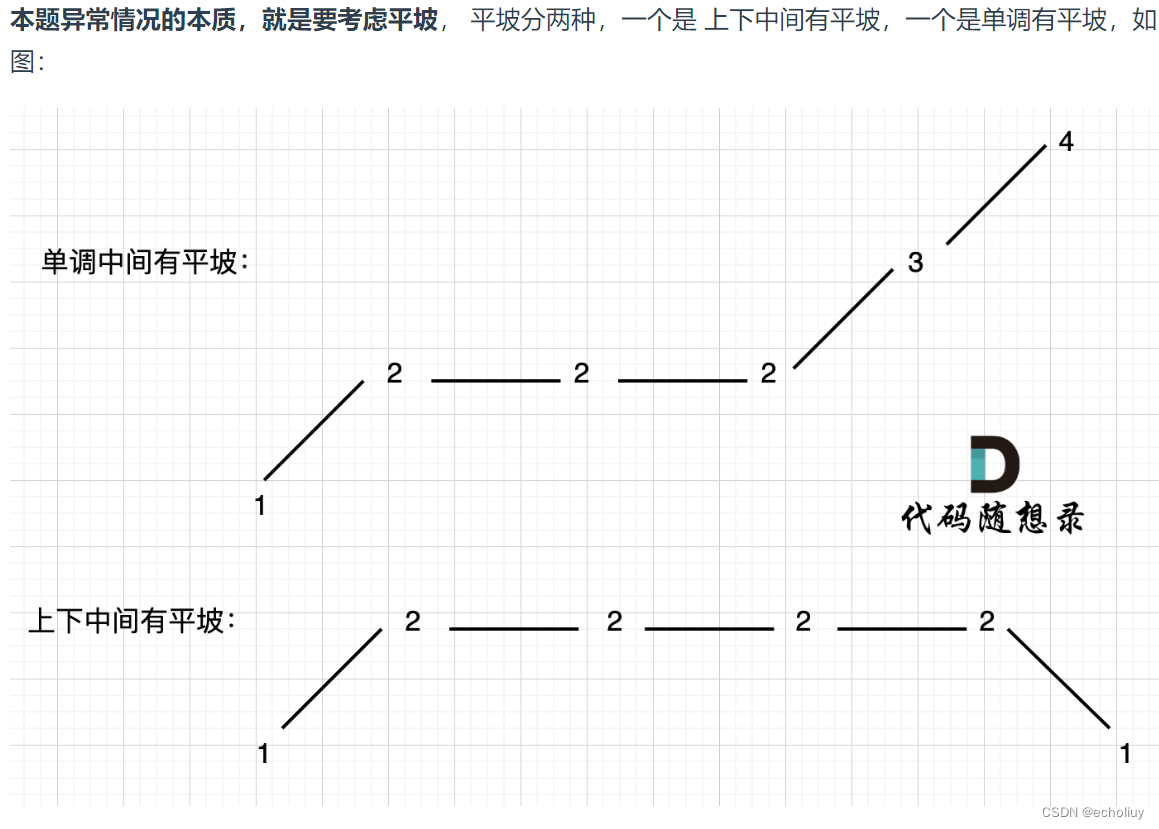
代码:
class Solution {public int wiggleMaxLength(int[] nums) {if (nums.length <= 1) {return nums.length;}//当前差值int curDiff = 0;//上一个差值int preDiff = 0;int count = 1;//默认最右边是峰值for (int i = 0; i < nums.length-1; i++) {//得到当前差值curDiff = nums[i+1] - nums[i];//如果当前差值和上一个差值为一正一负//等于0的情况表示初始时的preDiffif ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {count++;preDiff = curDiff;}}return count;}
}
思路二:动态规划(想不清楚)

代码:
class Solution {public int wiggleMaxLength(int[] nums) {// 0 i 作为波峰的最大长度// 1 i 作为波谷的最大长度int dp[][] = new int[nums.length][2];dp[0][0] = dp[0][1] = 1;for (int i = 1; i < nums.length; i++){//i 自己可以成为波峰或者波谷dp[i][0] = dp[i][1] = 1;for (int j = 0; j < i; j++){if (nums[j] > nums[i]){// i 是波谷dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);}if (nums[j] < nums[i]){// i 是波峰dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);}}}return Math.max(dp[nums.length - 1][0], dp[nums.length - 1][1]);}
最大子序和

思路:


代码:
class Solution {public int maxSubArray(int[] nums) {int sum = Integer.MIN_VALUE;int count = 0;for(int i=0;i<nums.length;i++){count+=nums[i];//?来判断是否结果是负数sum=Math.max(sum,count);// 取区间累计的最大值(相当于不断确定最大子序终止位置)if(count<0){//重置起始位置count=0;}}return sum;}
}
相关文章:

代码随想录算法训练营第31天|● 理论基础 ● 455.分发饼干 ● 376. 摆动序列 ● 53. 最大子序和
文章目录 理论基础分发饼干思路:代码: 摆动序列思路一 贪心算法:代码: 思路二:动态规划(想不清楚)代码: 最大子序和思路:代码: 理论基础 贪心算法其实就是没…...

无人机地面站技术,无人机地面站理论基础详解
地面站作为整个无人机系统的作战指挥中心,其控制内容包括:飞行器的飞行过程,飞行航迹, 有效载荷的任务功能,通讯链路的正常工作,以及 飞行器的发射和回收。 无人机地面站总述 地面站作为整个无人机系统的作战指挥中心…...

2024.2.13
21.C 22.D 23.B 5先出栈表示1,2,3,4已经入栈了,5出后4出,但之后想出1得先让3,2先后出栈,所以 B 不可能 24.10,12,120 25.2,5 26.可能会出现段错误…...

论文阅读:四足机器人对抗运动先验学习稳健和敏捷的行走
论文:Learning Robust and Agile Legged Locomotion Using Adversarial Motion Priors 进一步学习:AMP,baseline方法,TO 摘要: 介绍了一种新颖的系统,通过使用对抗性运动先验 (AMP) 使四足机器人在复杂地…...
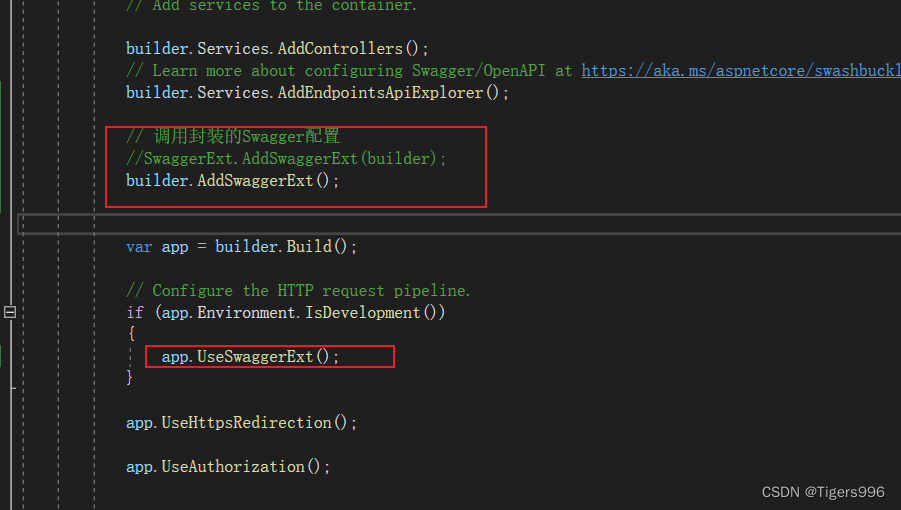
.NET Core WebAPI中封装Swagger配置
一、创建相关文件 创建一个Utility/SwaggerExt文件夹,添加一个类 二、在Program中找到Swagger相关配置信息 三、添加方法,在Program中调用 在SwaggerExt类中添加方法,将相关配置添写入 /// <summary> /// swagger配置 /// </sum…...

28. 找出字符串中第一个匹配项的下标
Problem: 28. 找出字符串中第一个匹配项的下标 文章目录 思路解题方法复杂度Code 思路 这个问题可以通过使用KMP(Knuth-Morris-Pratt)算法来解决。KMP算法是一种改进的字符串匹配算法,它的主要思想是当子串与目标字符串不匹配时,能…...

宿舍|学生宿舍管理小程序|基于微信小程序的学生宿舍管理系统设计与实现(源码+数据库+文档)
学生宿舍管理小程序目录 目录 基于微信小程序的学生宿舍管理系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、管理员模块的实现 (1)学生信息管理 (2)公告信息管理 (3)宿舍信息管理 &am…...
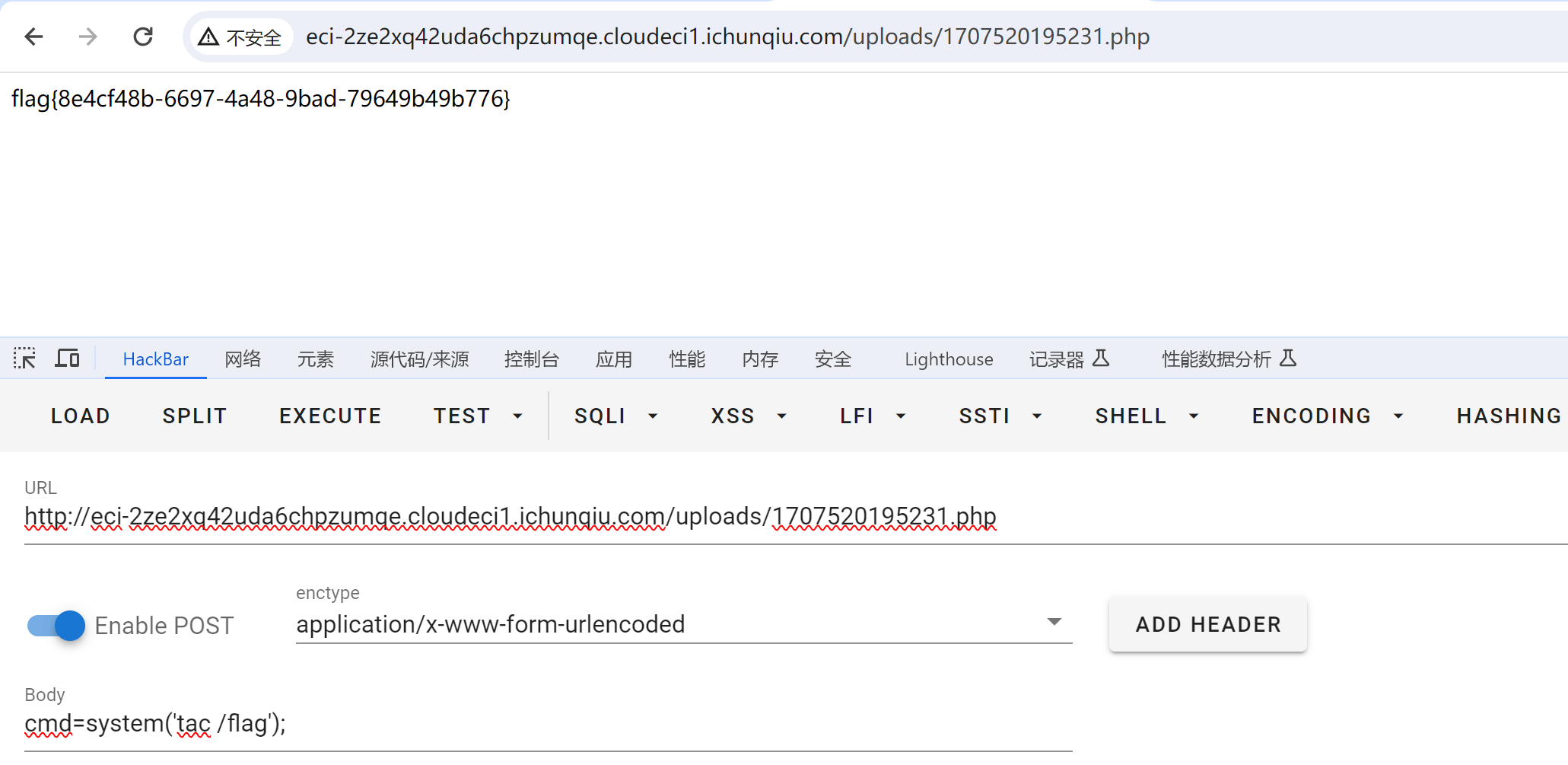
CVE-2022-25487 漏洞复现
漏洞描述:Atom CMS 2.0版本存在远程代码执行漏洞,该漏洞源于/admin/uploads.php 未能正确过滤构造代码段的特殊元素。攻击者可利用该漏洞导致任意代码执行。 其实这就是一个文件上传漏洞罢了。。。。 打开之后,/home路由是个空白 信息搜集&…...

C#面:强类型和弱类型
强类型 强类型是指在编程语言中,变量必须明确声明其数据类型,并且在编译时会进行类型检查的特性。它可以提高代码的可读性和可维护性,但有时需要显式地进行类型转换。换句话说,强类型语言要求变量的类型在编译时就要确定…...

nodejs和npm和vite
Nodejs 简单的说 Node.js 就是运行在服务端的 JavaScript。 Node.js 是一个基于 Chrome JavaScript 运行时建立的一个平台。 Node.js 是一个事件驱动 I/O 服务端 JavaScript 环境 用途: Node.js 可以被看作是一个 JavaScript 运行时环境,专门用于在服务…...
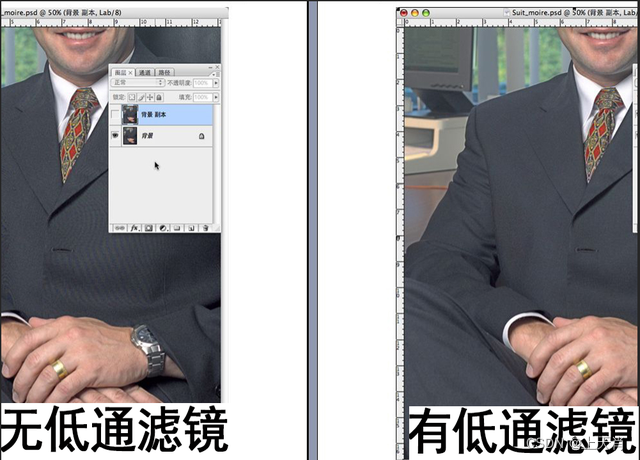
相机图像质量研究(24)常见问题总结:CMOS期间对成像的影响--摩尔纹
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...

Redis -- 数据库管理
目录 前言 切换数据库(select) 数据库中key的数量(dbsize) 清除数据库(flushall flushdb) 前言 MySQL有一个很重要的概念,那就是数据库database,一个MySQL里面有很多个database,一个datab…...
2023省赛真题:视频弹幕)
蓝桥杯(Web大学组)2023省赛真题:视频弹幕
思路: 主要是要仔细阅读题目以及理解给出的已有代码,进行函数间的调用、定时器的使用、元素移除、清除定时器等,注意细节。 笔记: height不要写成hight设置left时,记得加单位px可以获取left的值进行计算,但要注意sp…...

真假难辨 - Sora(OpenAI)/世界模拟器的技术报告
目录 引言技术报告汉译版英文原版 引言 Sora是OpenAI在2024年2月15日发布的世界模拟器,功能是通过文本可以生成一分钟的高保真视频。由于较高的视频质量,引起了巨大关注。下面是三个示例,在示例之后给出了其技术报告: tokyo-wal…...
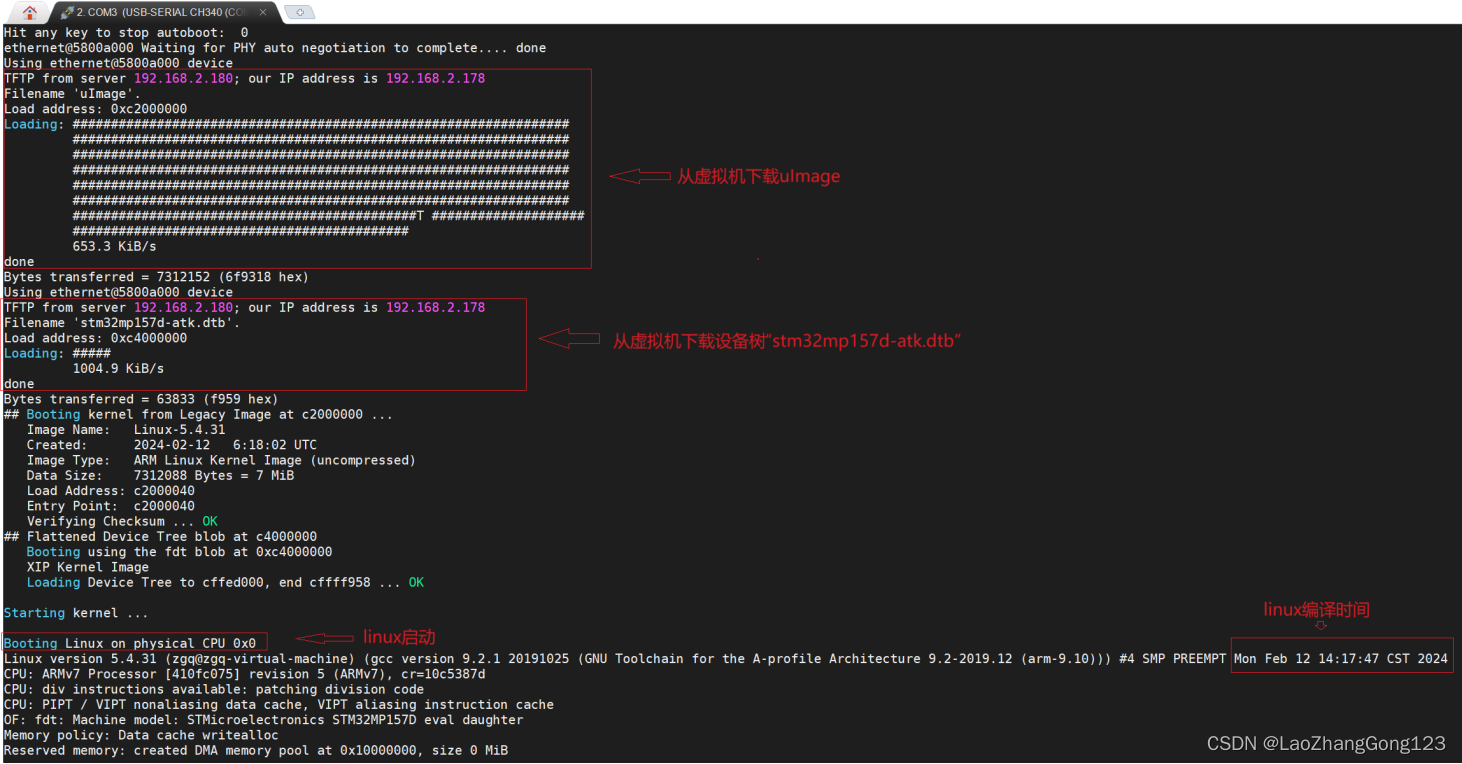
Linux第52步_移植ST公司的linux内核第4步_关闭内核模块验证和log信息时间戳_编译_并通过tftp下载测试
1、采用程序配置关闭“内核模块验证” 默认配置文件“stm32mp1_atk_defconfig”路径为“arch/arm/configs”; 使用VSCode打开默认配置文件“stm32mp1_atk_defconfg”,然后将下面的4条语句屏蔽掉,如下: CONFIG_MODULE_SIGy CONFIG_MODULE_…...
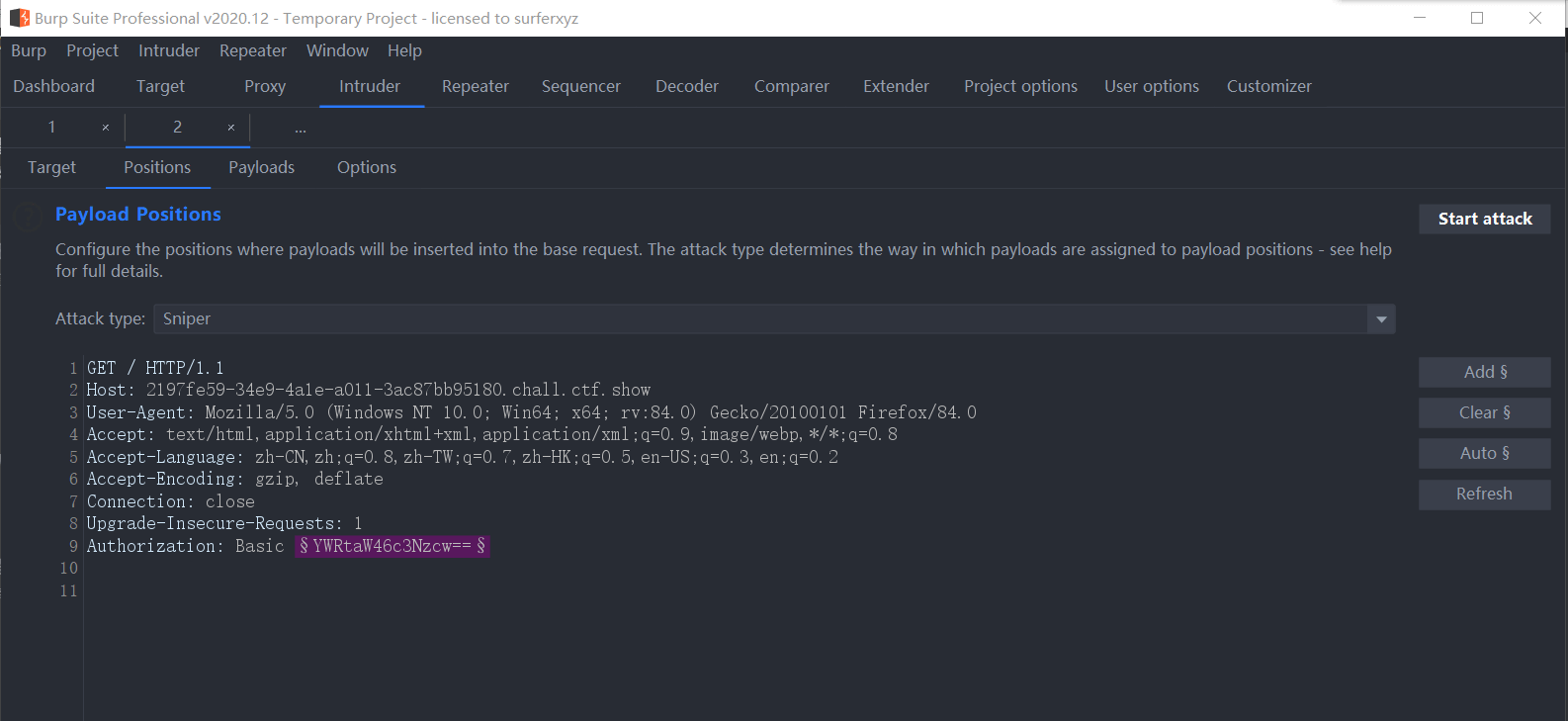
ctfshow-web21~28-WP
爆破(21-28) web21 题目给了一个zip文件,打开后解压是爆破的字典,我们抓包一下网址看看 发现账号和密码都被base64了,我们发送到intruder模块,给爆破的位置加上$符圈住 去base64解码一下看看格式...

鸿蒙开发系列教程(二十四)--List 列表操作(3)
列表编辑 1、新增列表项 定义列表项数据结构和初始化列表数据,构建列表整体布局和列表项。 提供新增列表项入口,即给新增按钮添加点击事件。 响应用户确定新增事件,更新列表数据。 2、删除列表项 列表的删除功能一般进入编辑模式后才可…...

线性代数笔记2--矩阵消元
0. 简介 矩阵消元 1. 消元过程 实例方程组 { x 2 y z 2 3 x 8 y z 12 4 y z 2 \begin{cases} x2yz2\\ 3x8yz12\\ 4yz2 \end{cases} ⎩ ⎨ ⎧x2yz23x8yz124yz2 矩阵化 A [ 1 2 1 3 8 1 0 4 1 ] X [ x y z ] A \begin{bmatrix} 1 & 2 & 1 \\ 3 & …...

透光力之珠——光耦固态继电器的独特特点解析
光耦固态继电器作为现代电子控制领域中的重要组件,以其独特的特点在工业、通信、医疗等多个领域得到广泛应用。本文将深入剖析光耦固态继电器的特点,揭示其在电子控制中的卓越性能。 光耦固态继电器的光电隔离技术 光耦固态继电器以其光电隔离技术而脱颖…...
)
C#系列-EntityFrameworkCore.Transactions.Abstractions应用场景+实例(38)
EntityFrameworkCore.Transactions.Abstractions应用场景 EntityFrameworkCore.Transactions.Abstractions 并不是一个官方的或广泛认可的 NuGet 包名称。在 Entity Framework Core (EF Core) 中,事务管理通常是通过 DbContext 的内置方法来实现的,如 Sa…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
