线性代数笔记2--矩阵消元
0. 简介
矩阵消元
1. 消元过程
实例方程组
{ x + 2 y + z = 2 3 x + 8 y + z = 12 4 y + z = 2 \begin{cases} x+2y+z=2\\ 3x+8y+z=12\\ 4y+z=2 \end{cases} ⎩ ⎨ ⎧x+2y+z=23x+8y+z=124y+z=2
矩阵化
A = [ 1 2 1 3 8 1 0 4 1 ] X = [ x y z ] A= \begin{bmatrix} 1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1 \end{bmatrix} \\ X= \begin{bmatrix} x\\y\\z \end{bmatrix} A= 130284111 X= xyz
B = [ 2 12 2 ] B= \begin{bmatrix} 2\\12\\2 \end{bmatrix} B= 2122
消元
[ 1 2 1 3 8 1 0 4 1 ] ⟶ ( 2 , 1 ) [ 1 2 1 0 2 − 2 0 4 1 ] ⟶ ( 3 , 2 ) [ 1 2 1 0 2 − 2 0 0 5 ] \begin{bmatrix} 1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1 \end{bmatrix} \stackrel{(2,1)}{\longrightarrow} \begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 4 & 1 \end{bmatrix} \stackrel{(3,2)}\longrightarrow \begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & -2\\ 0 & 0 & 5 \end{bmatrix} 130284111 ⟶(2,1) 1002241−21 ⟶(3,2) 1002201−25
回代
[ 2 12 2 ] ⟶ r o w 2 − 3 r o w 1 [ 2 6 2 ] ⟶ r o w 3 − 2 r o w 2 [ 2 6 − 10 ] \begin{bmatrix} 2 \\ 12 \\ 2 \end{bmatrix} \stackrel{row_2-3row_1}\longrightarrow \begin{bmatrix} 2 \\ 6 \\ 2 \end{bmatrix} \stackrel{row_3-2row_2}\longrightarrow \begin{bmatrix} 2 \\ 6 \\-10 \end{bmatrix} 2122 ⟶row2−3row1 262 ⟶row3−2row2 26−10
求解
[ 1 2 1 0 2 − 2 0 0 5 ] [ x y z ] = [ 2 6 − 10 ] \begin{bmatrix} 1 & 2 & 1\\ 0 & 2 & -2\\ 0 & 0 & 5 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\z \end{bmatrix} =\begin{bmatrix} 2 \\ 6 \\ -10 \end{bmatrix} 1002201−25 xyz = 26−10
结果
[ x y z ] = [ 2 1 − 2 ] \begin{bmatrix} x \\y \\z \end{bmatrix}= \begin{bmatrix} 2\\1 \\ -2 \end{bmatrix} xyz = 21−2
2. 消元矩阵
将上述消元的过程变为矩阵相乘的形式。
向量式思考
矩阵乘列向量
[ . . . . . . . . . ] [ x y z ] = [ x ∗ c o l 1 + y ∗ c o l 2 + z ∗ c o l 3 ] \begin{bmatrix} . & . & .\\ . & . & .\\ . & . & . \end{bmatrix} \begin{bmatrix}\ x \\ y\\ z \end{bmatrix}= \begin{bmatrix} x*col1 +y*col2 +z*col3 \end{bmatrix} ......... xyz =[x∗col1+y∗col2+z∗col3]
行向量乘矩阵
[ x y z ] [ . . . . . . . . . ] = [ x ∗ r o w 1 + y ∗ r o w 2 + z ∗ r o w 3 ] \begin{bmatrix}\ x \ y\ z \end{bmatrix} \begin{bmatrix} . & . & .\\ . & . & .\\ . & . & . \end{bmatrix}= \begin{bmatrix} x*row1 \\+\\y*row2 \\+\\z*row3 \end{bmatrix} [ x y z] ......... = x∗row1+y∗row2+z∗row3
一个矩阵左边乘一个单位矩阵并不改变其值
A = [ 1 2 1 3 8 1 0 4 1 ] = [ 1 0 0 0 1 0 0 0 1 ] [ 1 2 1 3 8 1 0 4 1 ] A= \begin{bmatrix} 1 & 2 & 1\\ 3 & 8 & 1\\ 0 & 4 & 1 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 1\\ 3 & 8 & 1\\ 0 & 4 & 1 \end{bmatrix} A= 130284111 = 100010001 130284111
而做行的加减则可以
A = [ 1 2 1 3 8 1 0 4 1 ] A ′ = [ 1 0 0 − 3 1 0 0 0 1 ] [ 1 2 1 3 8 1 0 4 1 ] = [ 1 2 1 0 2 − 2 0 4 1 ] A= \begin{bmatrix} 1 & 2 & 1\\ 3 & 8 & 1\\ 0 & 4 & 1 \end{bmatrix}\\ A'= \begin{bmatrix} 1 & 0 &0\\ -3 & 1 & 0\\ 0 &0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 1\\ 3 & 8 & 1\\ 0 & 4 &1 \end{bmatrix}=\\ \begin{bmatrix} 1 & 2 &1 \\ 0 & 2 & -2\\ 0& 4 & 1 \end{bmatrix} A= 130284111 A′= 1−30010001 130284111 = 1002241−21
实际上这个过程就是,我们在之前的消元过程中的第二行减去三倍第一行的过程。我们继续下去将这个矩阵对角化。
A ′ ′ = [ 1 0 0 0 1 0 0 − 2 1 ] A ′ = [ 1 0 0 0 1 0 0 − 2 1 ] [ 1 2 1 0 2 − 2 0 4 1 ] = [ 1 2 1 0 2 − 2 0 0 5 ] A''= \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & -2 & 1 \end{bmatrix} A'\\= \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & -2 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 1\\ 0 & 2 & -2 \\ 0 & 4 & 1 \end{bmatrix}\\= \begin{bmatrix} 1 & 2 & 1\\ 0 & 2 & -2\\ 0 & 0 & 5 \end{bmatrix} A′′= 10001−2001 A′= 10001−2001 1002241−21 = 1002201−25
我们令最后的上三角矩阵为
U = [ 1 2 1 0 2 − 2 0 0 5 ] U=\begin{bmatrix} 1 & 2 & 1\\ 0 & 2 & -2\\ 0 & 0 & 5 \end{bmatrix} U= 1002201−25
两个变换矩阵为
E 21 = [ 1 0 0 − 3 1 0 0 0 1 ] E 32 = [ 1 0 0 0 1 0 0 − 2 1 ] E_{21}=\begin{bmatrix} 1 & 0 &0\\ -3 & 1 & 0\\ 0 &0 & 1 \end{bmatrix} \\ E_{32}=\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & -2 & 1 \end{bmatrix} E21= 1−30010001 E32= 10001−2001
则 E 32 ( E 21 A ) = U E_{32}(E_{21}A)=U E32(E21A)=U
而矩阵乘法满足结合律证明即
E 32 E 21 A = E 32 ( E 21 A ) E_{32}E_{21}A=E_{32}(E_{21}A) E32E21A=E32(E21A)
所以最终消元的过程变成了寻找矩阵E的过程
E = E 32 E 21 E=E_{32}E_{21} E=E32E21
这一过程。
3. 置换矩阵
在上述的消元矩阵中,我们并没有进行列的交换。那么如何进行交换呢?
我们知道在原矩阵基础左边乘单位矩阵,矩阵不会发生变化。
A = [ 1 2 3 4 ] = [ 1 0 0 1 ] [ 1 2 3 4 ] A= \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}=\ \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} A=[1324]= [1001][1324]
如何交换两行呢,将单位矩阵变形
A ′ = [ 0 1 1 0 ] [ 1 2 3 4 ] = [ 3 4 1 2 ] A'= \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}= \begin{bmatrix} 3 & 4\\ 1 & 2 \end{bmatrix} A′=[0110][1324]=[3142]
推广到多行
A = [ 1 2 3 4 5 6 7 8 9 ] A= \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} A= 147258369
- 行变换
交换第一行和第三行
A ′ = [ 0 0 1 0 1 0 1 0 0 ] [ 1 2 3 4 5 6 7 8 9 ] A'= \begin{bmatrix} 0 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} A′= 001010100 147258369
交换第一行和第二行
A ′ ′ = [ 0 1 0 1 0 0 0 0 1 ] [ 1 2 3 4 5 6 7 8 9 ] A''= \begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} A′′= 010100001 147258369
所以交换任意两行,只需将单位矩阵中对应行 1 1 1的位置进行交换。
- 列变换
在矩阵左边乘是对原矩阵行变换,而在矩阵右边则是列变换
交换矩阵两列
A = [ 1 2 3 4 ] A ′ = [ 1 2 3 4 ] [ 0 1 1 0 ] = [ 2 1 4 3 ] A= \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} \\ A'= \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}= \begin{bmatrix} 2 & 1\\ 4 & 3 \end{bmatrix} A=[1324]A′=[1324][0110]=[2413]
交换多列也是一样的效果
交换第 1 1 1第 2 2 2列
A = [ 1 2 3 4 5 6 7 8 9 ] A ′ = [ 1 2 3 4 5 6 7 8 9 ] [ 0 1 0 1 0 0 0 0 1 ] = [ 2 1 3 5 4 6 8 7 9 ] A= \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{bmatrix} \\ A'= \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{bmatrix} \begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1\\ \end{bmatrix}= \begin{bmatrix} 2 & 1 & 3\\ 5 & 4 & 6\\ 8 & 7 & 9\\ \end{bmatrix} A= 147258369 A′= 147258369 010100001 = 258147369
所以交换任意两列,只需将单位矩阵中对应行 1 1 1的位置进行交换。
与行交换的不同地方在于,矩阵乘的在右边了。
4. 矩阵的逆
A = [ 1 0 0 − 3 1 0 0 0 1 ] A − 1 = [ 1 0 0 3 1 0 0 0 1 ] A − 1 A = [ 1 0 0 3 1 0 0 0 1 ] [ 1 0 0 − 3 1 0 0 0 1 ] = [ 1 0 0 0 1 0 0 0 1 ] A= \begin{bmatrix} 1 & 0 & 0\\ -3 & 1 &0\\ 0 & 0 & 1 \end{bmatrix}\\ A^{-1}= \begin{bmatrix} 1 & 0 & 0\\ 3 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix}\\ A^{-1}A= \begin{bmatrix} 1 & 0 & 0\\ 3 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\ -3 & 1 &0\\ 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 &0\\ 0 & 0 & 1 \end{bmatrix} A= 1−30010001 A−1= 130010001 A−1A= 130010001 1−30010001 = 100010001
相关文章:

线性代数笔记2--矩阵消元
0. 简介 矩阵消元 1. 消元过程 实例方程组 { x 2 y z 2 3 x 8 y z 12 4 y z 2 \begin{cases} x2yz2\\ 3x8yz12\\ 4yz2 \end{cases} ⎩ ⎨ ⎧x2yz23x8yz124yz2 矩阵化 A [ 1 2 1 3 8 1 0 4 1 ] X [ x y z ] A \begin{bmatrix} 1 & 2 & 1 \\ 3 & …...

透光力之珠——光耦固态继电器的独特特点解析
光耦固态继电器作为现代电子控制领域中的重要组件,以其独特的特点在工业、通信、医疗等多个领域得到广泛应用。本文将深入剖析光耦固态继电器的特点,揭示其在电子控制中的卓越性能。 光耦固态继电器的光电隔离技术 光耦固态继电器以其光电隔离技术而脱颖…...
)
C#系列-EntityFrameworkCore.Transactions.Abstractions应用场景+实例(38)
EntityFrameworkCore.Transactions.Abstractions应用场景 EntityFrameworkCore.Transactions.Abstractions 并不是一个官方的或广泛认可的 NuGet 包名称。在 Entity Framework Core (EF Core) 中,事务管理通常是通过 DbContext 的内置方法来实现的,如 Sa…...

PMDG 737
在Simbrief中生成计划后下载两个文件 放到C:\Users\32497\AppData\Local\Packages\Microsoft.FlightSimulator_8wekyb3d8bbwe\LocalState\packages\pmdg-aircraft-737(微软商店版本) 加油 先在飞行计划中查看计划燃油数量 MCDU中, AIRPLANE SEVICE 第二页, REQUEST FUEL TR…...

深入探索Midjourney:领航人工智能的新征程
深入探索Midjourney:领航人工智能的新征程 引言 在这个数据驱动、以技术创新为核心的时代,Midjourney以其独特的特性在人工智能领域中崭露头角。作为一款前沿的人工智能工具,它不仅重新定义了人机交互的方式,而且为各行各业提供…...
ChatGPT高效提问—prompt实践(漏洞风险分析-重构建议-识别内存泄漏)
ChatGPT高效提问—prompt实践(漏洞风险分析-重构建议-识别内存泄漏) 1.1 漏洞和风险分析 ChatGPT还可以帮助开发人员预测代码的潜在风险,识别其中的安全漏洞,而不必先运行它,这可以让开发人员及早发现错误࿰…...

【AIGC】Stable Diffusion 的提示词入门
一、正向提示词和反向提示词 Stable Diffusion 中的提示词通常用于指导用户对生成的图像进行控制。这些提示词可以分为正向提示词(Positive Prompts)和反向提示词(Negative Prompts)两类,它们分别影响图像生成过程中的…...
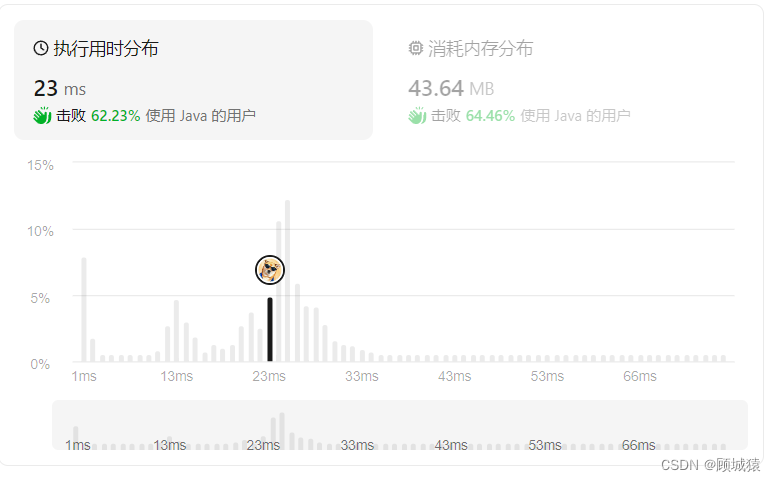
力扣---通配符匹配
题目描述: 给你一个输入字符串 (s) 和一个字符模式 (p) ,请你实现一个支持 ? 和 * 匹配规则的通配符匹配: ? 可以匹配任何单个字符。 * 可以匹配任意字符序列(包括空字符序列)。 判定匹配成功的充要条件是ÿ…...

Rust 原生类型
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、标量类型(scalar type)二、 复合类型(compound type)总结 前言 Rust 学习系列 ,rust中的原生类…...
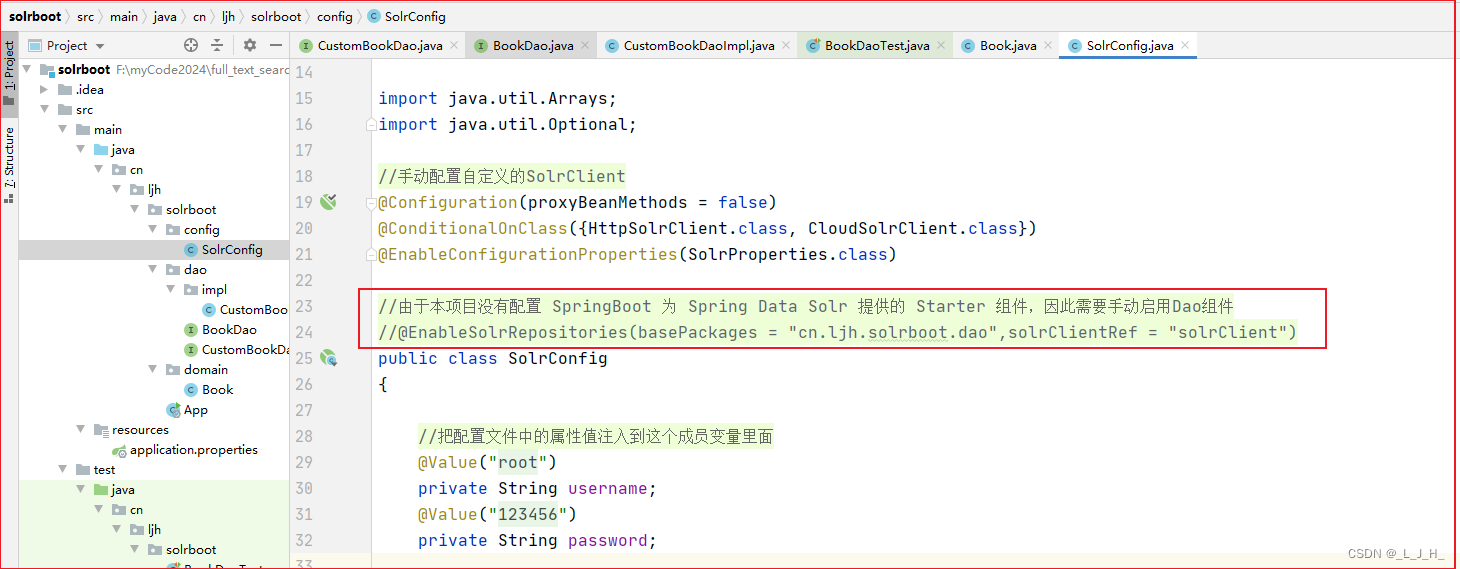
09、全文检索 -- Solr -- SpringBoot 整合 Spring Data Solr (生成DAO组件 和 实现自定义查询方法)
目录 SpringBoot 整合 Spring Data SolrSpring Data Solr的功能(生成DAO组件):Spring Data Solr大致包括如下几方面功能:Query查询(属于半自动)代码演示:1、演示通过dao组件来保存文档1、实体类…...

C# CAD SelectionFilter下TypedValue数组
SelectionFilter是用于过滤AutoCAD实体的类,在AutoCAD中,可以使用它来选择具有特定属性的实体。构造SelectionFilter对象时,需要传入一个TypedValue数组,它用于定义选择规则。 在TypedValue数组中,每个元素表示一个选…...

python 爬虫篇(3)---->Beautiful Soup 网页解析库的使用(包含实例代码)
Beautiful Soup 网页解析库的使用 文章目录 Beautiful Soup 网页解析库的使用前言一、安装Beautiful Soup 和 lxml二、Beautiful Soup基本使用方法标签选择器1 .string --获取文本内容2 .name --获取标签本身名称3 .attrs[] --通过属性拿属性的值标准选择器find_all( name , at…...

第十二周学习报告
比赛 参加了一场 div 2 ,B 题,C 题没写出来,B 是一个排序去重+双指针,C题是要观察出一个数学结论(因为数据范围太大,我暴力做直接超时了) 排 6253 ,表现分是 998 &…...

Redis面试题整理(持续更新)
1. 缓存穿透? 缓存穿透是指查询一个一定不存在的数据,如果从存储层查不到数据则不写入缓存,这将导致这个不存在的数据每次请求都要到 DB 去查询,可能导致DB挂掉,这种情况大概率是遭到了攻击。 解决方案: …...
一周学会Django5 Python Web开发-Django5 Hello World编写
锋哥原创的Python Web开发 Django5视频教程: 2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~共计14条视频,包括:2024版 Django5 Python we…...
讲解用Python处理Excel表格
我们今天来一起探索一下用Python怎么操作Excel文件。与word文件的操作库python-docx类似,Python也有专门的库为Excel文件的操作提供支持,这些库包括xlrd、xlwt、xlutils、openpyxl、xlsxwriter几种,其中我最喜欢用的是openpyxl,这…...

WEB APIs(1)
变量声明const(修饰常量) const优先,如react,基本const, 对于引用数据类型,可用const声明,因为储存的是地址 何为APIs 可以使用js操作HTML和浏览器 分类:DOM(文档对象…...

C++重新入门-基本输入输出
C 的 I/O 发生在流中,流是字节序列。如果字节流是从设备(如键盘、磁盘驱动器、网络连接等)流向内存,这叫做输入操作。如果字节流是从内存流向设备(如显示屏、打印机、磁盘驱动器、网络连接等),这…...

【C语言】解析刘谦春晚魔术《守岁共此时》
今年的春晚上刘谦表演了魔术《守岁共此时》,台上台下积极互动(尤其是小尼),十分的有趣。刘谦老师的魔术不仅仅是他的高超手法,还有这背后的严谨逻辑,下面我们来用C语言来解析魔术吧。 源代码 #define _CRT…...

剑指offer——数值的整数次方
目录 1. 题目描述2. 一般思路2.1 有问题的思路2.2 全面但不高效的思路2.3 面试小提示 3. 全面又高效的思路 1. 题目描述 题目:实现函数 double Power(double base,int exponent),求base 的exponent 次方。不得使用库函数,同时不需要考虑大数问题 2. 一般…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
