剑指offer——数值的整数次方
目录
- 1. 题目描述
- 2. 一般思路
- 2.1 有问题的思路
- 2.2 全面但不高效的思路
- 2.3 面试小提示
- 3. 全面又高效的思路
1. 题目描述
- 题目:实现函数 double Power(double base,int exponent),求base 的exponent 次方。不得使用库函数,同时不需要考虑大数问题
2. 一般思路
2.1 有问题的思路
- 由于不需要考虑大数问题,这道题看起来很简单,可能不少应聘者在看到题目30秒后就能写出如下的代码:
#include <stdio.h>float Power(double base, int exponent)
{double result = 1.0;for (int i = 0; i < exponent; i++){result *= base;}return result;
}int main()
{double base = 0;int exponent = 0;scanf("%lf %d", &base, &exponent);printf("%lf", Power(base, exponent));return 0;
}
- 运行结果为:
- 不过遗憾的是,写得快不一定就能得到面试官的青睐,
- 因为面试官会问要是输入的指数(exponent)小于1
- 即是零和负数的时候怎么办?上面的代码完全没有考虑,只包括了指数是正数的情况。
2.2 全面但不高效的思路
- 我们知道当指数为负数的时候,可以先对指数求绝对值,然后算出次方的结果之后再取倒数。
- 既然有求倒数,我们很自然就要想到有没有可能对0求倒数,如果对0求倒数怎么办?
- 当底数(base)是零且指数是负数的时候,如果不做特殊处理,就会出现对0求倒数从而导致程序运行出错。怎么告诉函数的调用者出现了这种错误?
- 前面提到我们可以采用3种方法返回值、全局代码和异常。
- 面试的时候可以向面试官阐述每种方法的优缺点,然后一起讨论决定选用哪种方式。
- 最后需要指出的是,由于0的0次方在数学上是没有意义的,因此无论是输出0还是1都是可以接受的,
- 但这都需要和面试官说清楚,表明我们已经考虑到这个边界值了。
- 有了这些相对而言已经全面很多的考虑,我们就可以把最初的代码修改如下:
#define wucha 0.00000001
#include <stdio.h>
#include <math.h>float Power(double base, int exponent)
{if (abs(base) < wucha){return 0.0;}//底数为0,(底数指数都为0则结果默认为0)if (exponent == 0){return 1.0;}//指数为0double result = 1.0;if (exponent > 0){for (int i = 0; i < exponent; i++){result *= base;}return result;}//指数为正else if (exponent < 0){for (int i = 0; i > exponent; i--){result *= base;}return 1 / result;}//指数为负
}int main()
{double base = 0;int exponent = 0;while (scanf("%lf %d", &base, &exponent) != EOF){printf("%lf\n", Power(base, exponent));}return 0;
}
- 运行结果为:
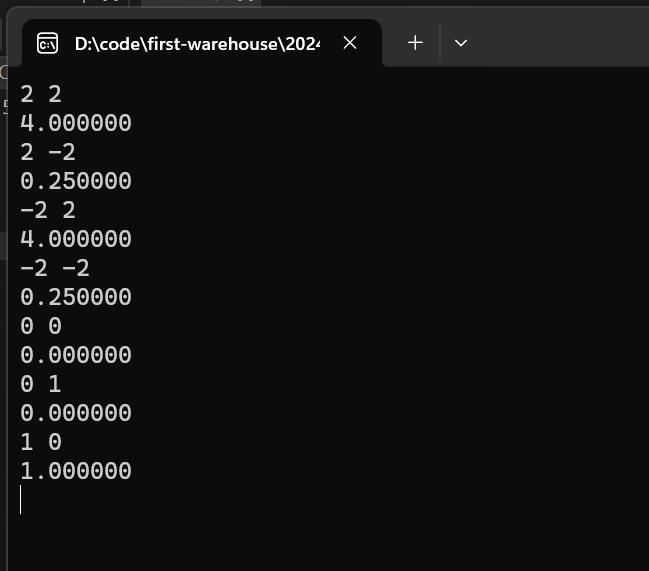
- 一个细节值得我们注意:在判断底数base是不是等于0时,不能直接写base=-0,
- 这是因为在计算机内表示小数时(包括 foat和 double 型小数)都有误差。判断两个小数是否相等,只能判断它们之差的绝对值是不是在一个很小的范围内。
- 如果两个数相差很小,就可以认为它们相等。
2.3 面试小提示
- 由于计算机表示小数(包括 foat和 double 型小数)都有误差,我们不能直接用等号(==)判断两个小数是否相等。如果两个小数的差的绝对值很小,比如小于 0.0000001,就可以认为它们相等。
3. 全面又高效的思路
- 此时我们考虑得已经很周详了,已经能够达到很多面试官的要求了。
- 但是如果我们碰到的面试官是一个在效率上追求完美的人,那么他有可能会提醒我们函数 Power还有更快的办法。
- 如果输入的指数 exponent为32,我们在函数 Power的循环中需要做 31次乘法。
- 但我们可以换一种思路考虑:我们的目标是求出一个数字的 32次方,如果我们已经知道了它的16次方,那么只要在 16 次方的基础上再平方一次就可以了。而16次方是8次方的平方。
- 这样以此类推,我们求32次方只需要做5次乘法:先求平方,在平方的基础上求4次方,在4次方的基础上求8次方,在8次方的基础上求16次方,最后在16次方的基础上求32次方。
- 也就是说,我们可以用如下公式求a的n次方:
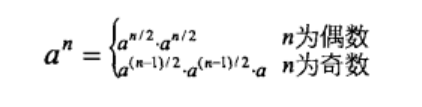
- 代码如下:
#include <stdio.h>float Power2(double base, unsigned int exponent)
{if (exponent == 0){return 1;}if (exponent == 1){return base;}double result = Power2(base, exponent >> 1);result *= result;if (exponent & 1 == 1){result *= result;}return result;
}int main()
{double base = 0;unsigned int exponent = 0;while (scanf("%lf %d", &base, &exponent) != EOF){printf("%lf\n", Power2(base, exponent));}return 0;
}
- 但是美中不足的是这个代码只能求非负数的非负数幂
最后,
恭喜你又遥遥领先了别人!

相关文章:

剑指offer——数值的整数次方
目录 1. 题目描述2. 一般思路2.1 有问题的思路2.2 全面但不高效的思路2.3 面试小提示 3. 全面又高效的思路 1. 题目描述 题目:实现函数 double Power(double base,int exponent),求base 的exponent 次方。不得使用库函数,同时不需要考虑大数问题 2. 一般…...

Tied Block Convolution: 具有共享较薄滤波器的更简洁、更出色的CNN
摘要 https://arxiv.org/pdf/2009.12021.pdf 卷积是卷积神经网络(CNN)的主要构建块。我们观察到,随着通道数的增加,优化后的CNN通常具有高度相关的滤波器,这降低了特征表示的表达力。我们提出了Tied Block Convolutio…...
算法沉淀——BFS 解决 FloodFill 算法(leetcode真题剖析)
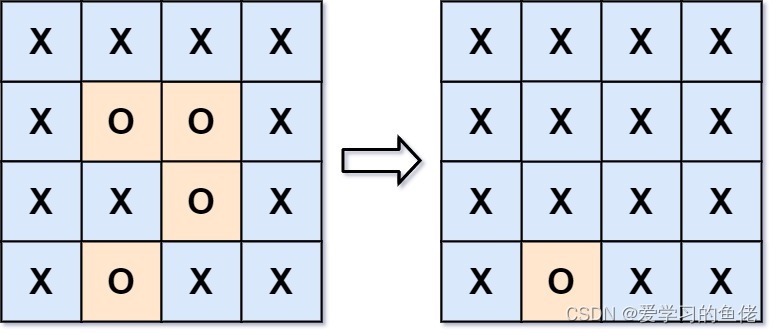
算法沉淀——BFS 解决 FloodFill 算法 01.图像渲染02.岛屿数量03.岛屿的最大面积04.被围绕的区域 BFS(广度优先搜索)解决 Flood Fill 算法的基本思想是通过从起始点开始,逐层向外扩展,访问所有与起始点相连且具有相同特性…...
wordpress外贸成品网站模板
首页大图slider轮播,橙色风格的wordpress外贸网站模板 https://www.zhanyes.com/waimao/6250.html 蓝色经典风格的wordpress外贸建站模板 https://www.zhanyes.com/waimao/6263.html...
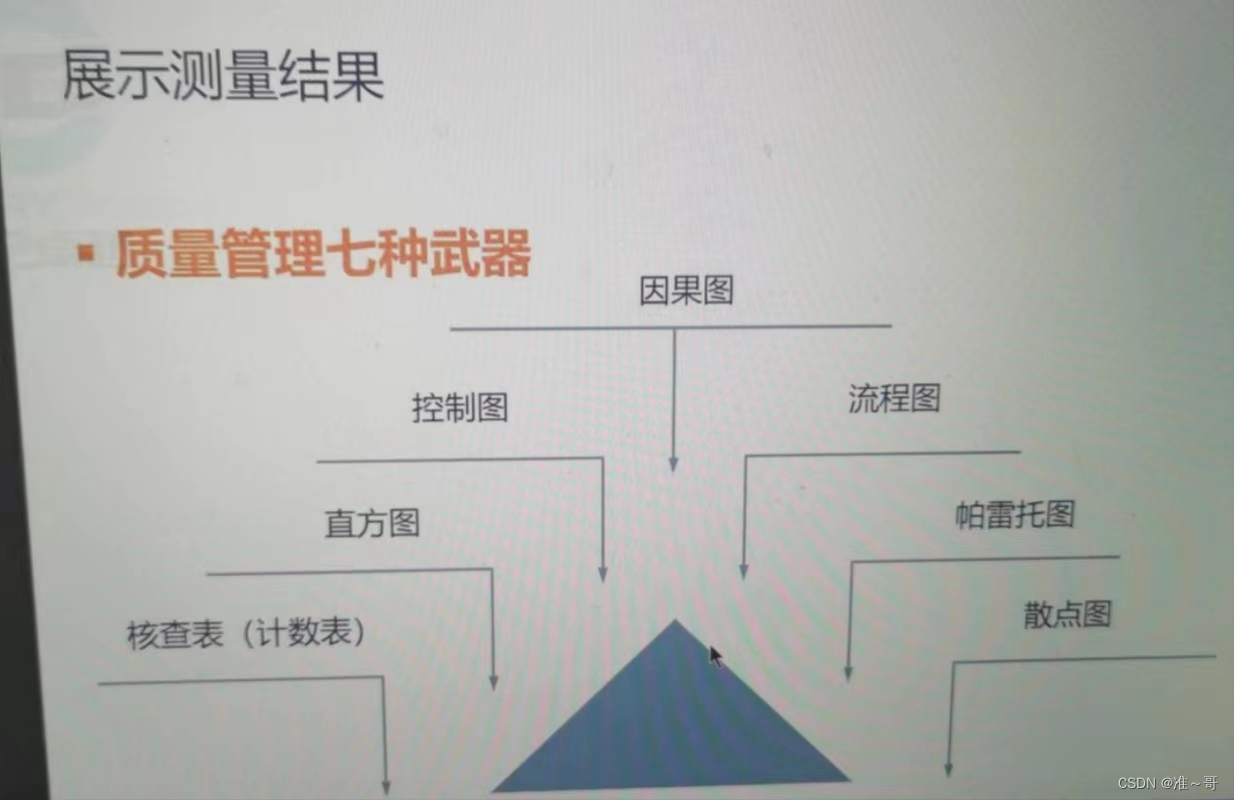
如何使用六图一表七种武器
六图一表七种武器用于质量管理: 描述当遇到问题时应该用那张图来解决: 一、如果题目说出了质量问题需要找原因? 解:用因果图,因果图也称石川图或鱼骨图 二、如果要判断过程是否稳定受控? 解:…...

阿里云游戏服务器租用费用价格组成,费用详单
阿里云游戏服务器租用价格表:4核16G服务器26元1个月、146元半年,游戏专业服务器8核32G配置90元一个月、271元3个月,阿里云服务器网aliyunfuwuqi.com分享阿里云游戏专用服务器详细配置和精准报价: 阿里云游戏服务器租用价格表 阿…...
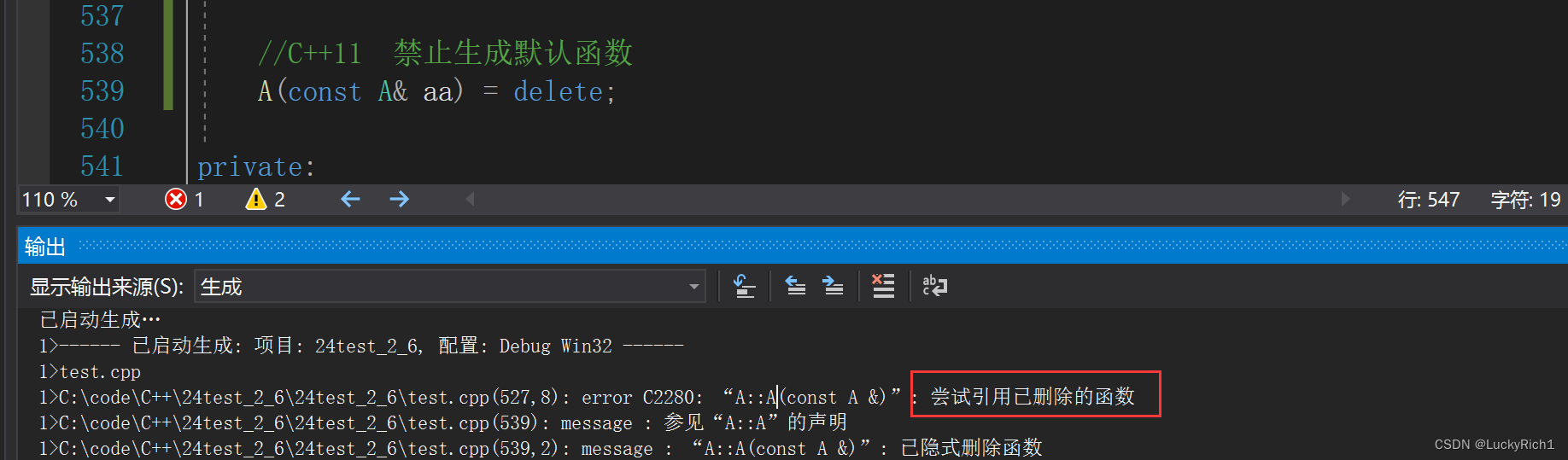
【C++】C++11上
C11上 1.C11简介2.统一的列表初始化2.1 {} 初始化2.2 initializer_list 3.变量类型推导3.1auto3.2decltype3.3nullptr 4.范围for循环5.final与override6.智能指针7. STL中一些变化8.右值引用和移动语义8.1左值引用和右值引用8.2左值引用与右值引用比较8.3右值引用使用场景和意义…...

【前端高频面试题--git篇】
🚀 作者 :“码上有前” 🚀 文章简介 :前端高频面试题 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 前端高频面试题--git篇 往期精彩内容常用命令git add 和 git stage 有什么区别怎么使用git连接…...

c++创建对象
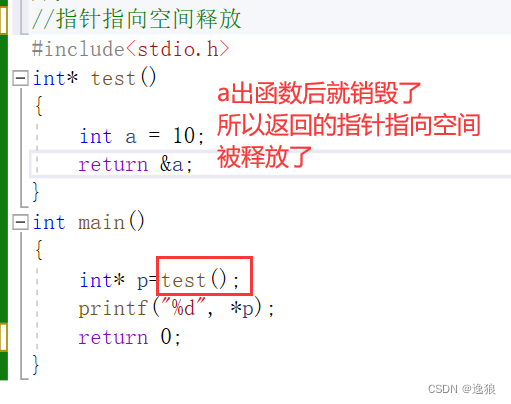
c创建对象 1.声明一个对象,然后使用默认构造函数来创建对象: class MyClass { public:MyClass() {// 构造函数代码} };int main() {MyClass obj; // 声明并创建一个对象return 0; }2.使用new和指针动态创建对象:不会自动释放 使用 new 运算…...

软件实例分享,洗车店系统管理软件会员卡电子系统教程
软件实例分享,洗车店系统管理软件会员卡电子系统教程 一、前言 以下软件教程以 佳易王洗车店会员管理软件V16.0为例说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 1、会员卡号可以绑定车牌号或手机号 2、卡号也可以直接使用手机号&a…...

【Docker进阶】镜像制作-用Dockerfile制作镜像(一)
进阶一 docker镜像制作 文章目录 进阶一 docker镜像制作用dockerfile制作镜像dockerfile是什么dockerfile格式为什么需要dockerfileDockerfile指令集合FROMMAINTAINERLABELCOPYENVWORKDIR 用dockerfile制作镜像 用快照制作镜像的缺陷: 黑盒不可重复臃肿 docker…...

数据密集型应用系统设计
数据密集型应用系统设计 原文完整版PDF:https://pan.quark.cn/s/d5a34151fee9 这本书的作者是少有的从工业界干到学术界的牛人,知识面广得惊人,也善于举一反三,知识之间互相关联,比如有个地方把读路径比作programming …...
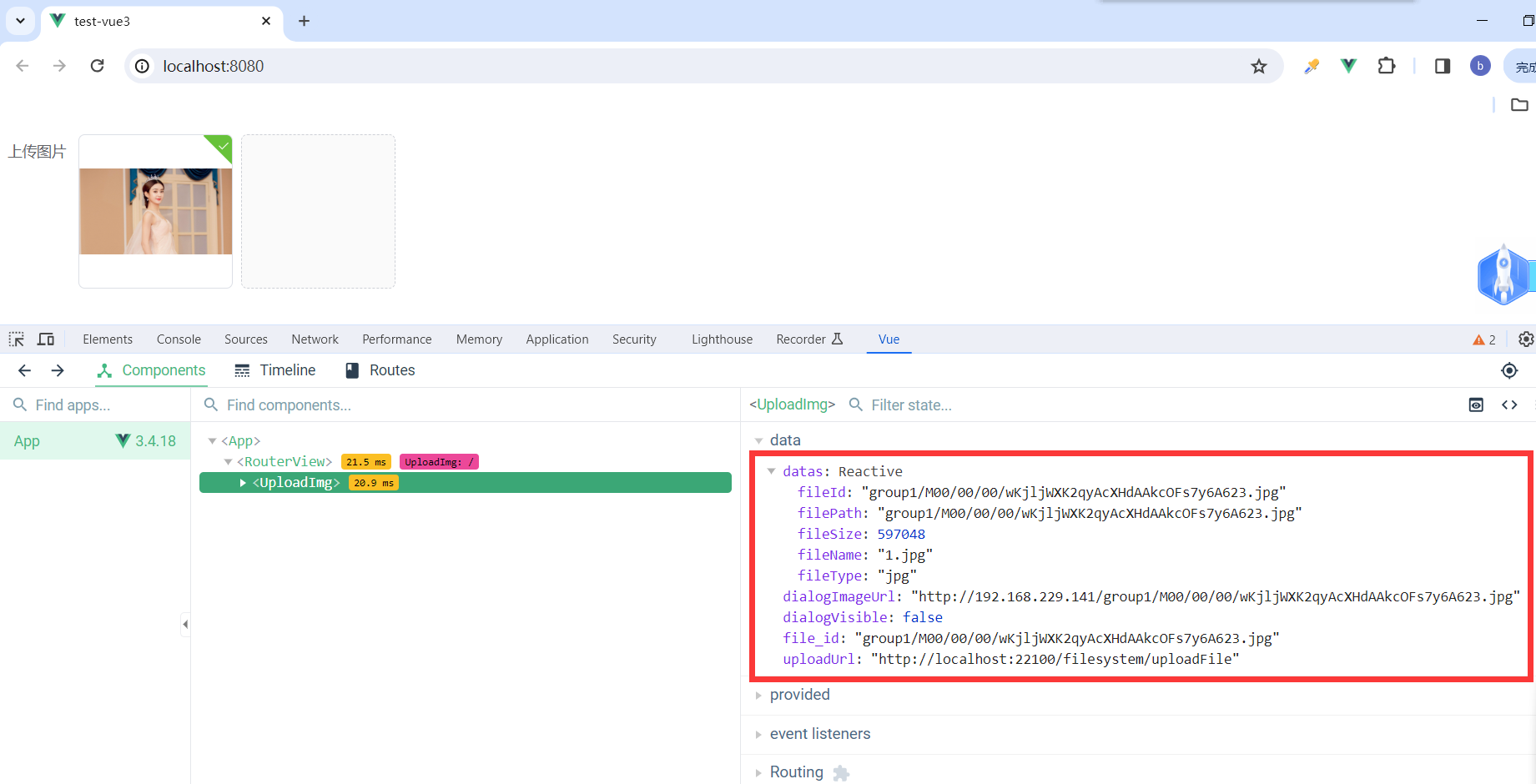
分布式文件系统 SpringBoot+FastDFS+Vue.js【一】
分布式文件系统 SpringBootFastDFSVue.js【一】 一、分布式文件系统1.1.文件系统1.2.什么是分布式文件系统1.3.分布式文件系统的出现1.3.主流的分布式文件系统1.4.分布式文件服务提供商1.4.1.阿里OSS1.4.2.七牛云存储1.4.3.百度云存储 二、fastDFS2.1.fastDSF介绍2.2.为什么要使…...
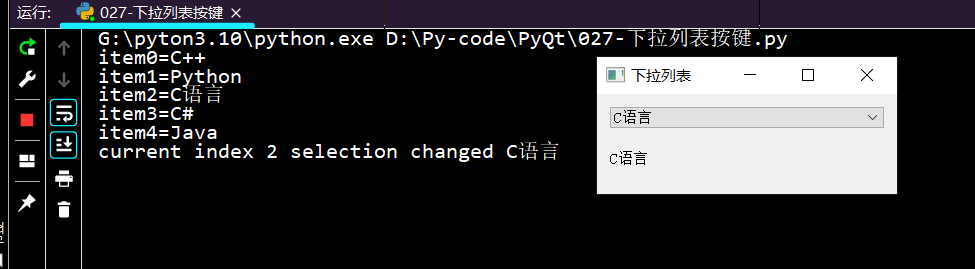
【PyQt】11-QTextEdit、QPushButton
文章目录 前言一、文本输入-QTextEdit1.1 代码1.2 运行结果 二、QPushButton2.1.1 按钮上添加文本2.1.2 按键的弹跳效果2.1.3 两个信号可以绑定一个槽。2.1.4 带图标的按键运行结果 2.1.5 按键不可用以及回车默认完整代码2.2 单选按键控件运行结果 2.3 复选框(多选框…...
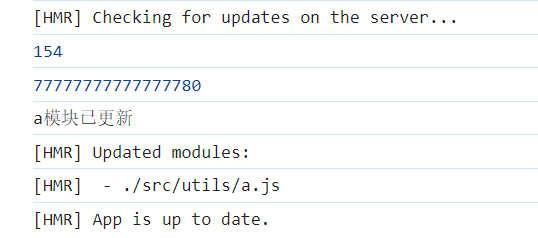
初识webpack(二)解析resolve、插件plugins、dev-server
目录 (一)webpack的解析(resolve) 1.resovle.alias 2.resolve.extensions 3.resolve.mainFiles (二) plugin插件 1.CleanWebpackPlugin 2.HtmlWebpackPlugin 3.DefinePlugin (三)webpack-dev-server 1.开启本地服务器 2.HMR模块热替换 3.devServer的更多配置项 (…...
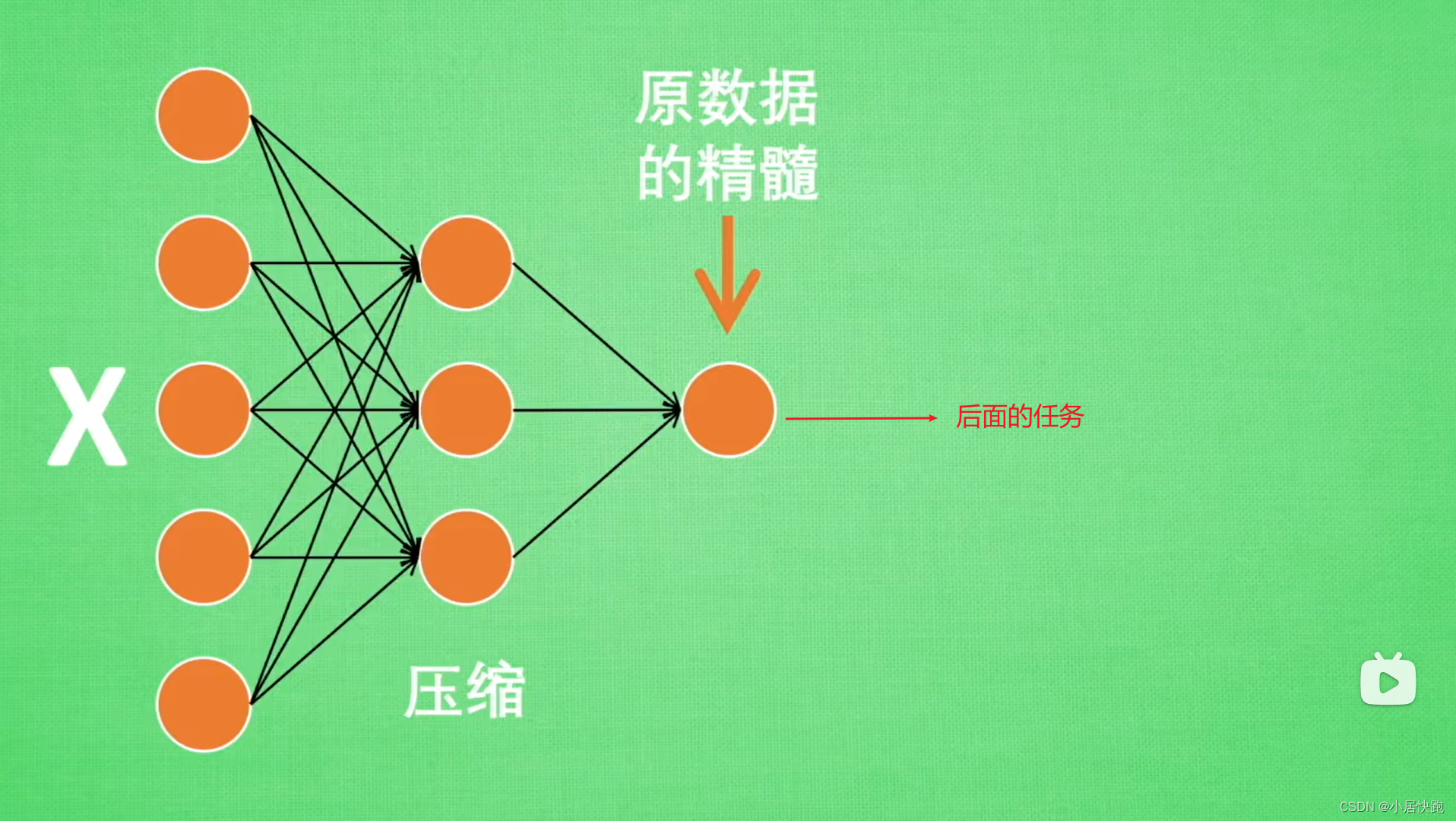
什么是自编码器Auto-Encoder?
来源:https://www.bilibili.com/video/BV1Vx411j78H/?spm_id_from333.1007.0.0&vd_sourcef66cebc7ed6819c67fca9b4fa3785d39 为什么要压缩呢? 让神经网络直接从上千万个神经元中学习是一件很吃力的事情,因此通过压缩提取出原图片中最具代…...

openGauss学习笔记-219 openGauss性能调优-确定性能调优范围-硬件瓶颈点分析-网络
文章目录 openGauss学习笔记-219 openGauss性能调优-确定性能调优范围-硬件瓶颈点分析-网络219.1 查看网络状况 openGauss学习笔记-219 openGauss性能调优-确定性能调优范围-硬件瓶颈点分析-网络 获取openGauss节点的CPU、内存、I/O和网络资源使用情况,确认这些资源…...
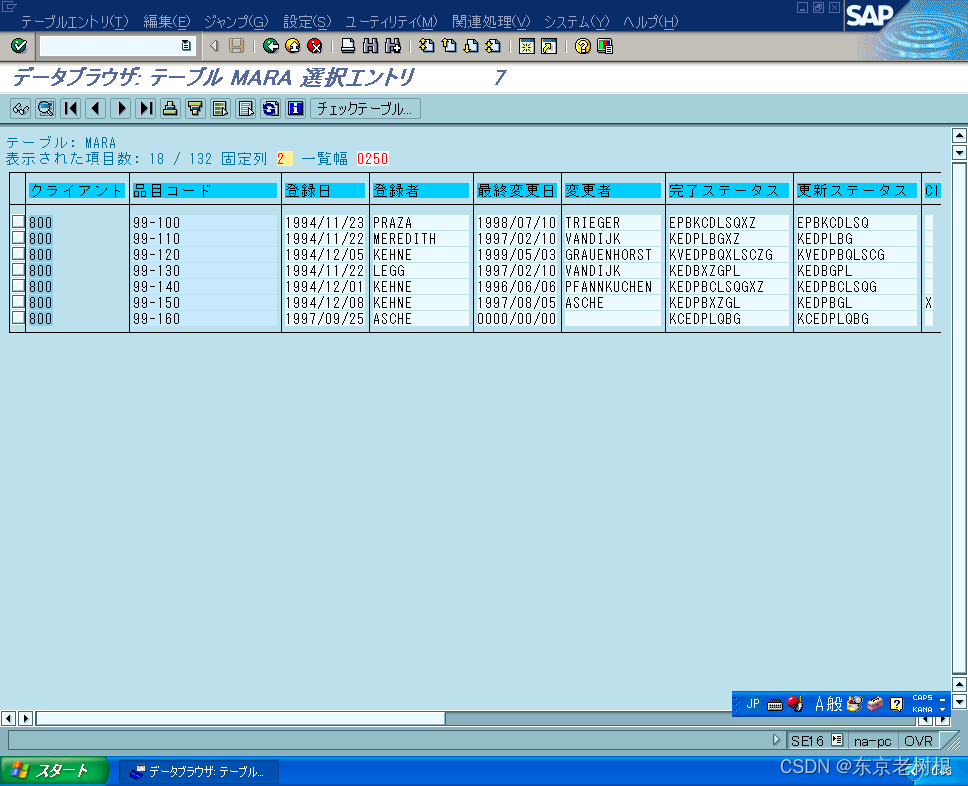
SAP PP学习笔记- 豆知识01 - 怎么查询既存品目
SAP系统当中已经有哪些品目要怎么查询呢? 1,MM60 品目一览 这里可以输入Plant,然后可以查询该工厂的所有品目。 2,SE16 > MARA MARA 品目一般Data,存放的是品目基本信息。 如果要查询该品目属于哪个Plant&#x…...

相机的机身马达有什么用?
新手疑问: 为什么我的尼康D3200相机明明拥有拍视频能力,但是拍摄视频时却不能对焦 科普时间 那是因为你的相机缺少机身马达,并且你所使用的镜头也没有马达!机身马达是用于给镜头提供对焦动力的装置。它的作用是使相机具备自动对焦功能。如…...
拿捏c语言指针(上)
目录 前言 编辑 指针 内存与地址 计算机常见单位 理解编址 取地址,指针变量,解引用 取地址 指针变量 解引用 指针变量大小 指针类型的作用 char*解引用后 指针-整数 应用 void*指针 const修饰指针变量 const修饰普通变量 const修饰指…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...
