线性代数的本质 2 线性组合、张成的空间、基
基于3Blue1Brown视频的笔记
一种新的看待方式
对于一个向量,比如说,如何看待其中的3和-2?
一开始,我们往往将其看作长度(从向量的首走到尾部,分别在x和y上走的长度)。
在有了数乘后,我们可以将其视为对向量进行缩放的标量,缩放的对象是两个特殊的向量 和
,这两个向量也被称为xy坐标系的基向量。
也就是有:
这种把向量看作向量的数乘的和的思想正体现了数乘和相加是线性代数的核心。

这里很自然引出一个问题,可不可以换另外的向量作基向量?
比如这里我们用 和
,想象一下任意缩放这两个向量,然后相加,得到不同的结果。
感性上,我们可以得到所有二维平面中的向量;实际上,确实如此。
具体为什么,以及在这样的基下,坐标和向量的关系,可以暂且往后放。目前需要认识到的是,每当我们用数字描述向量时,它都依赖于我们正在使用的基。
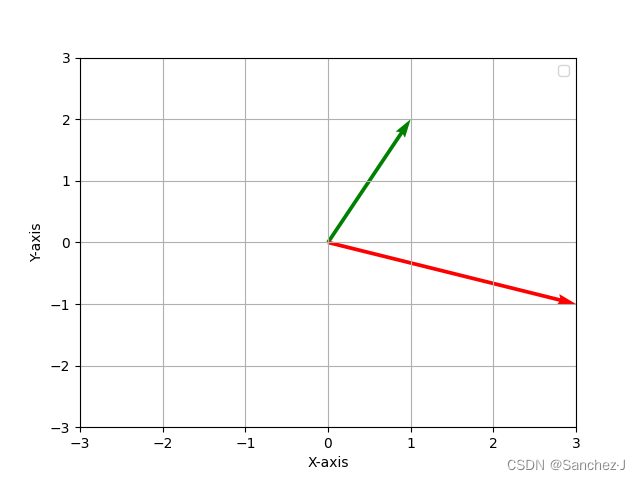
线性组合
两个数乘向量的和被称为这两个向量的线性组合。在xy坐标系,任意取两个向量进行线性组合时,组合出的所有向量实际上有3种情况:
- 两个向量都是零向量时,只能得到零向量。
- 两个向量恰好在一条直线上时,得到的向量终点也全在这条直线上。
- 其余情况,能得到整个平面所有向量。
张成的空间
这里又引入一点术语:
所有可以表示为给定向量线性组合的向量的集合,称为给定向量张成的空间。
所以,对于大多数二维向量来说,它们张成的空间是整个二维平面的向量;但当共线时,它们张成的空间就是终点落在一条直线上的向量的集合。
我们可以总结,张成的空间实际上就是在问:仅仅通过向量加法与向量数乘这两种基础运算,能获得的所有向量的集合是什么?
向量与点
由于在线性代数中,向量的起点总是在原点,因此可以直接用终点坐标来表示向量,即用点来表示向量。
线性相关/无关
在三维坐标系中,先取两个不共线的向量,两者张成以一个平面,然后再取一个向量,如果没有落在这个平面,那么三者的线性组合可以得到整个三维空间的所有向量。
而当这第3个向量恰好落在前两个向量张成的平面里时,三者张成的空间没有变化,至少有一个向量对张成的空间没有贡献,可以删去而不减小张成的空间,这种情况称它们是线性相关的前面两个向量共线的情况也是如此。
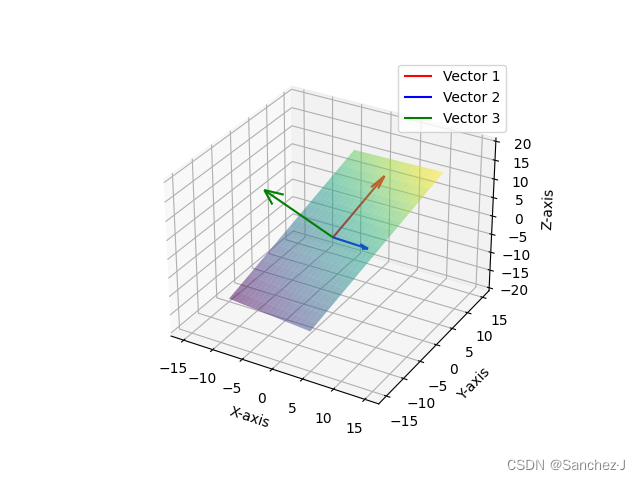
另一种对于线性相关等效的描述是:其中一个向量能被其他向量的线性组合表示(因为这个向量已经落在它们张成的空间中了)
而如果每一个向量都不是多余的,都给张成的空间增添了新的维度,那么我们称它们线性无关
基
基(basis)是什么在前文已经提到过了,其严格定义是:
向量空间的一组基是张成该空间的一个线性无关的向量集
相关文章:

线性代数的本质 2 线性组合、张成的空间、基
基于3Blue1Brown视频的笔记 一种新的看待方式 对于一个向量,比如说,如何看待其中的3和-2? 一开始,我们往往将其看作长度(从向量的首走到尾部,分别在x和y上走的长度)。 在有了数乘后࿰…...

- 工程实践 - 《QPS百万级的有状态服务实践》01 - 存储选型实践
本文属于专栏《构建工业级QPS百万级服务》 《QPS百万级的无状态服务实践》已经完成。截止目前为止,支持需求“给系统传入两个日期,计算间隔有多少天”的QPS百万级服务架构已经完成。如图1: 图1 可是这个架构不能满足需求“给系统传入两个日期…...
SECS/GEM的HSMS通讯?金南瓜方案
High Speed SECS Message Service (HSMS) 是一种基于 TCP/IP 的协议,它使得 SECS 消息通信更加快速。这通常用作设备间通信的接口。 HSMS 状态逻辑变化(序列): 1.Not Connected:准备初始化 TCP/IP 连接,但尚…...

wayland(xdg_wm_base) + egl + opengles——dma_buf 作为纹理数据源(五)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、EGL dma_buf import 相关的数据结构和函数1. EGLImageKHR2. eglCreateImageKHR()3. glEGLImageTargetTexture2DOES()二、egl 中 import dma_buf 作为纹理的代码实例1. egl_wayland_dmabuf_…...

【VTKExamples::PolyData】第二十八期 LinearExtrusion
很高兴在雪易的CSDN遇见你 VTK技术爱好者 QQ:870202403 前言 本文分享VTK样例LinearExtrusion,并解析接口vtkLinearExtrusionFilter,希望对各位小伙伴有所帮助! 感谢各位小伙伴的点赞+关注,小易会继续努力分享,一起进步! 你的点赞就是我的动力(^U^)ノ~YO 目录…...
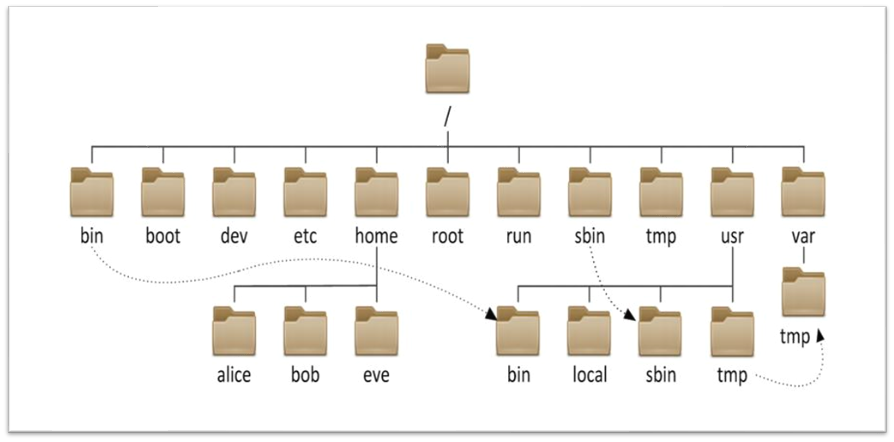
Linux操作系统基础(五):Linux的目录结构
文章目录 Linux的目录结构 一、Linux目录与Windows目录区别 二、常见目录介绍(记住重点) Linux的目录结构 一、Linux目录与Windows目录区别 Linux的目录结构是一个树型结构 Windows 系统 可以拥有多个盘符, 如 C盘、D盘、E盘 Linux 没有盘符 这个概…...

SolidWorks如何在一个零件的基础上绘制另一个零件
经过测试,新建零件,然后插入零件a,在a的基础上绘制b,这种做法无法断开a与b的联系。虽然可以通过切除命令,切除b,但不是正途。 在装配体中可以实现: (1)建立装配体 (2&…...
)
gin(结)
gin day1 今天的目标就是学懂,看懂每一步代码。 gin框架 gin框架就是go语言的web框架。框架你也可以理解成一个库。里面有一堆封装好的工具,帮你实现各种各样的功能,这样使得你可以关注业务本身,而在写代码上少费力。 快速入门&…...

JavaScript 设计模式之桥接模式
桥接模式 通过桥接模式,我们可以将业务逻辑与元素的事件解耦,也可以更灵活的创建一些对象 倘若我们有如下代码 const dom document.getElementById(#test)// 鼠标移入移出事件 // 鼠标移入时改变背景色和字体颜色 dom.onmouseenter function() { th…...

B3651 [语言月赛202208] 数组调整
题目描述 给出一个长度为 n 的数组,第 i 个数为ai。 为了调整这个数组,需要将第 k 个数改变为 −ak。 请你求出调整后的数组中所有数的和。 输入格式 输入共两行。 输入的第一行为两个整数 n,k。 输入的第二行为 n 个整数,第 i 个…...
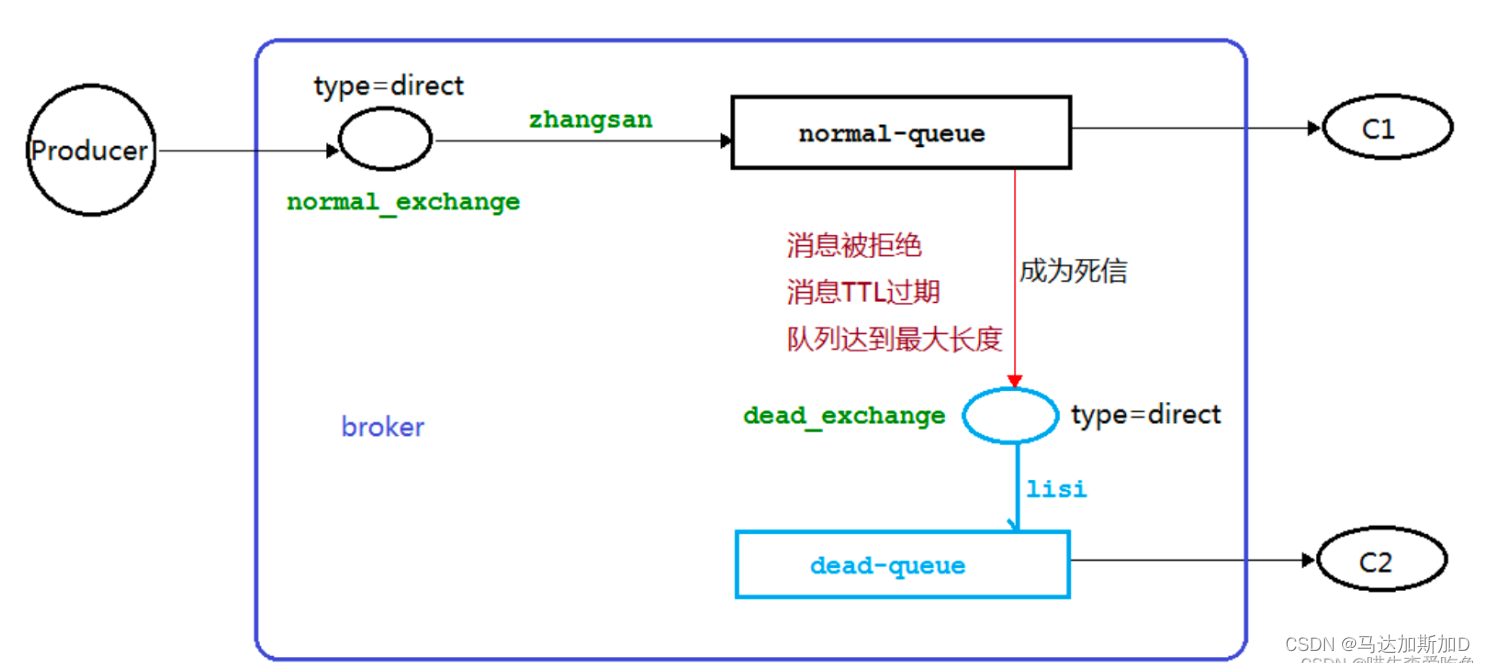
MessageQueue --- RabbitMQ
MessageQueue --- RabbitMQ RabbitMQ IntroRabbitMQ 核心概念RabbitMQ 分发类型Dead letter (死信)保证消息的可靠传递 RabbitMQ Intro 2007年发布,是一个在AMQP(高级消息队列协议)基础上完成的,可复用的企业消息系统,…...
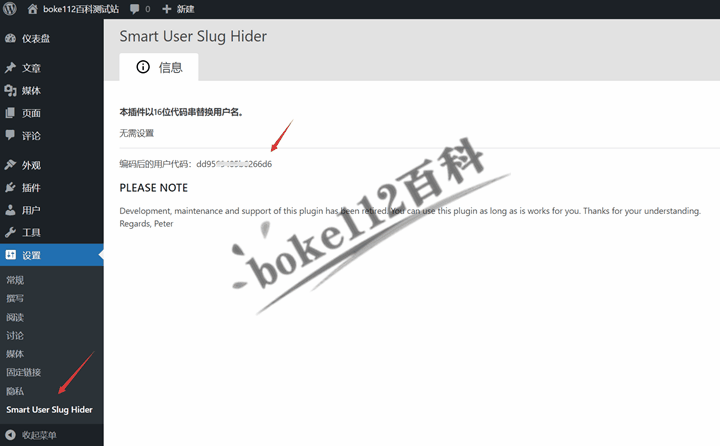
WordPress作者页面链接的用户名自动变成16位字符串串插件Smart User Slug Hider
WordPress默认的作者页面URL链接地址格式为“你的域名/author/admin”,其中admin就是你的用户名,这样的话就会暴露我们的用户名。 为了解决这个问题,前面boke112百科跟大家分享了『如何将WordPress作者存档链接中的用户名改为昵称或ID』一文…...

Nvidia 携手 RTX 推出的本地运行 AI 聊天机器人
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
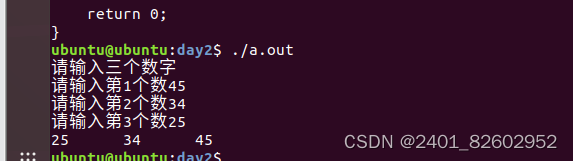
年假作业day2
1.打印字母图形 #include<stdio.h> #include<string.h> int main(int argc, const char *argv[]) { int i,j; char k; for(i1;i<7;i) { for(j1;j<i;j) { printf("%c",_); } for(j0,…...

HTML-多媒体嵌入-MDN文档学习笔记
HTML-多媒体与嵌入 查看更多学习笔记:GitHub:LoveEmiliaForever MDN中文官网 HTML-中的图片 将图片放入网页 可以使用<img/>来将图片嵌入网页,它是一个空元素,最少只需src属性即可工作 <img src"图片链接"…...

openJudge | 距离排序 C语言
总时间限制: 1000ms 内存限制: 65536kB 描述 给出三维空间中的n个点(不超过10个),求出n个点两两之间的距离,并按距离由大到小依次输出两个点的坐标及它们之间的距离。 输入 输入包括两行,第一行包含一个整数n表示点的个数,第二…...

【教程】MySQL数据库学习笔记(三)——数据定义语言DDL(持续更新)
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【MySQL数据库学习】系列文章 第一章 《认识与环境搭建》 第二章 《数据类型》 第三章 《数据定义语言DDL》 文章目录 【MyS…...
)
[leetcode]买卖股票的最佳时机 (动态规划)
121. 买卖股票的最佳时机 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从…...

隐函数的求导【高数笔记】
1. 什么是隐函数? 2. 隐函数的做题步骤? 3. 隐函数中的复合函数求解法,与求导中复合函数求解法有什么不同? 4. 隐函数求导的过程中需要注意什么?...
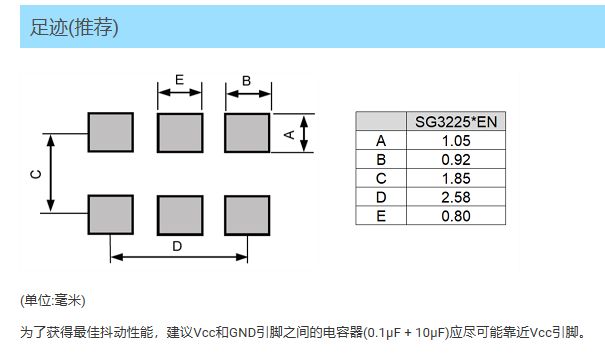
SG3225EEN晶体振荡器规格书
SG3225EEN 晶振是EPSON/爱普生的一款额定频率25 MHz至500 MHz的石英晶体振荡器,6脚贴片,LV-PECL输出,3225封装常规有源晶振,具有小尺寸,轻薄型,高稳定性,低相位抖动,低电源电压&…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
