深度学习之梯度下降算法
梯度下降算法
- 梯度下降算法
- 数学公式
- 结果
- 梯度下降算法存在的问题
- 随机梯度下降算法
梯度下降算法
数学公式


这里案例是用梯度下降算法,来计算 y = w * x
先计算出梯度,再进行梯度的更新
import numpy as np
import matplotlib.pyplot as pltx_data = [1.0, 2.0, 3.0, 4.0]
y_data = [2.0, 4.0, 6.0, 8.0]mse_list= []
w_list = []w = 1.0 #注意:这里设初始权重为1.0
def forward(x):return w*x
def const(xs, ys):const = 0for x, y in zip(xs, ys):y_pred = forward(x)const += (y_pred - y)**2return const/ len(xs)def gradient(xs, ys):grad = 0for x, y in zip(xs, ys):grad += 2 * x * (w * x - y)return grad / len(xs)print('Predict (befortraining)',4,forward(4))#100轮
for epoch in range(100):const_val = const(x_data, y_data) #损失值,为了绘图,才算他grad_val = gradient(x_data, y_data) # gradient函数求梯度值w = w - 0.01 * grad_val#这里学习率取的 0.01,要尽量小mse_list.append(const_val)print('Epoch:', epoch, 'w=', w, 'cost=', const_val)
print('Predict(after training)', 4, forward(4))#绘图
w_list = np.arange(0, 100, 1)
plt.plot(w_list, mse_list)
plt.xlabel("epoch")
plt.ylabel("mse")
plt.show()
结果
Predict (befortraining) 4 4.0
Epoch: 0 w= 1.15 cost= 7.5
Epoch: 1 w= 1.2774999999999999 cost= 5.418750000000001
Epoch: 2 w= 1.385875 cost= 3.9150468750000016
Epoch: 3 w= 1.47799375 cost= 2.828621367187501
Epoch: 4 w= 1.5562946874999999 cost= 2.0436789377929685
Epoch: 5 w= 1.6228504843749998 cost= 1.4765580325554204
Epoch: 6 w= 1.6794229117187498 cost= 1.0668131785212922
Epoch: 7 w= 1.7275094749609374 cost= 0.7707725214816338
Epoch: 8 w= 1.7683830537167968 cost= 0.55688314677048
Epoch: 9 w= 1.8031255956592773 cost= 0.40234807354167157
Epoch: 10 w= 1.8326567563103857 cost= 0.29069648313385765
Epoch: 11 w= 1.857758242863828 cost= 0.21002820906421227
Epoch: 12 w= 1.8790945064342537 cost= 0.15174538104889318
Epoch: 13 w= 1.8972303304691156 cost= 0.10963603780782546
Epoch: 14 w= 1.9126457808987483 cost= 0.07921203731615392
Epoch: 15 w= 1.925748913763936 cost= 0.05723069696092115
Epoch: 16 w= 1.9368865766993457 cost= 0.041349178554265495
Epoch: 17 w= 1.9463535901944438 cost= 0.02987478150545676
Epoch: 18 w= 1.9544005516652772 cost= 0.021584529637692605
Epoch: 19 w= 1.9612404689154856 cost= 0.015594822663232907
Epoch: 20 w= 1.9670543985781628 cost= 0.011267259374185785
Epoch: 21 w= 1.9719962387914383 cost= 0.00814059489784921
Epoch: 22 w= 1.9761968029727226 cost= 0.0058815798136960945
Epoch: 23 w= 1.9797672825268142 cost= 0.004249441415395416
Epoch: 24 w= 1.9828021901477921 cost= 0.0030702214226231784
Epoch: 25 w= 1.9853818616256234 cost= 0.0022182349778452353
Epoch: 26 w= 1.9875745823817799 cost= 0.0016026747714931776
Epoch: 27 w= 1.989438395024513 cost= 0.0011579325224038112
Epoch: 28 w= 1.991022635770836 cost= 0.0008366062474367442
Epoch: 29 w= 1.9923692404052107 cost= 0.0006044480137730437
Epoch: 30 w= 1.993513854344429 cost= 0.0004367136899510165
Epoch: 31 w= 1.9944867761927647 cost= 0.00031552564098961234
Epoch: 32 w= 1.99531375976385 cost= 0.00022796727561499308
Epoch: 33 w= 1.9960166957992724 cost= 0.0001647063566318346
Epoch: 34 w= 1.9966141914293816 cost= 0.00011900034266650408
Epoch: 35 w= 1.9971220627149744 cost= 8.597774757655033e-05
Epoch: 36 w= 1.9975537533077283 cost= 6.211892262405537e-05
Epoch: 37 w= 1.9979206903115692 cost= 4.488092159587483e-05
Epoch: 38 w= 1.9982325867648338 cost= 3.242646585301842e-05
Epoch: 39 w= 1.9984976987501089 cost= 2.3428121578803835e-05
Epoch: 40 w= 1.9987230439375925 cost= 1.692681784068377e-05
Epoch: 41 w= 1.9989145873469536 cost= 1.2229625889894448e-05
Epoch: 42 w= 1.9990773992449105 cost= 8.835904705448865e-06
Epoch: 43 w= 1.999215789358174 cost= 6.383941149688757e-06
Epoch: 44 w= 1.9993334209544478 cost= 4.612397480649774e-06
Epoch: 45 w= 1.9994334078112805 cost= 3.33245717977035e-06
Epoch: 46 w= 1.9995183966395884 cost= 2.4077003123843227e-06
Epoch: 47 w= 1.9995906371436503 cost= 1.7395634756983151e-06
Epoch: 48 w= 1.9996520415721026 cost= 1.2568346111911193e-06
Epoch: 49 w= 1.9997042353362873 cost= 9.080630065859313e-07
Epoch: 50 w= 1.9997486000358442 cost= 6.560755222580743e-07
Epoch: 51 w= 1.9997863100304676 cost= 4.7401456483160105e-07
Epoch: 52 w= 1.9998183635258975 cost= 3.4247552309066444e-07
Epoch: 53 w= 1.999845608997013 cost= 2.4743856543302625e-07
Epoch: 54 w= 1.999868767647461 cost= 1.7877436352529204e-07
Epoch: 55 w= 1.9998884525003418 cost= 1.2916447764716773e-07
Epoch: 56 w= 1.9999051846252904 cost= 9.332133510001552e-08
Epoch: 57 w= 1.999919406931497 cost= 6.742466460983543e-08
Epoch: 58 w= 1.9999314958917724 cost= 4.8714320180508126e-08
Epoch: 59 w= 1.9999417715080066 cost= 3.5196096330379474e-08
Epoch: 60 w= 1.9999505057818057 cost= 2.542917959872535e-08
Epoch: 61 w= 1.999957929914535 cost= 1.8372582260029613e-08
Epoch: 62 w= 1.9999642404273548 cost= 1.327419068279643e-08
Epoch: 63 w= 1.9999696043632516 cost= 9.590602768272778e-09
Epoch: 64 w= 1.9999741637087638 cost= 6.929210500056835e-09
Epoch: 65 w= 1.9999780391524493 cost= 5.006354586314298e-09
Epoch: 66 w= 1.999981333279582 cost= 3.617091188568193e-09
Epoch: 67 w= 1.9999841332876447 cost= 2.6133483837386546e-09
Epoch: 68 w= 1.999986513294498 cost= 1.888144207242458e-09
Epoch: 69 w= 1.9999885363003234 cost= 1.3641841897252644e-09
Epoch: 70 w= 1.999990255855275 cost= 9.856230770713489e-10
Epoch: 71 w= 1.9999917174769837 cost= 7.121126731808042e-10
Epoch: 72 w= 1.9999929598554362 cost= 5.145014063749241e-10
Epoch: 73 w= 1.9999940158771208 cost= 3.7172726609486193e-10
Epoch: 74 w= 1.9999949134955526 cost= 2.6857294975413565e-10
Epoch: 75 w= 1.9999956764712197 cost= 1.9404395619846422e-10
Epoch: 76 w= 1.9999963250005368 cost= 1.4019675835727846e-10
Epoch: 77 w= 1.9999968762504563 cost= 1.0129215790946163e-10
Epoch: 78 w= 1.9999973448128878 cost= 7.318358408922187e-11
Epoch: 79 w= 1.9999977430909546 cost= 5.2875139505922e-11
Epoch: 80 w= 1.9999980816273113 cost= 3.820228829502065e-11
Epoch: 81 w= 1.9999983693832146 cost= 2.7601153294430312e-11
Epoch: 82 w= 1.9999986139757324 cost= 1.994183325506297e-11
Epoch: 83 w= 1.9999988218793725 cost= 1.4407974526944569e-11
Epoch: 84 w= 1.9999989985974667 cost= 1.0409761596639575e-11
Epoch: 85 w= 1.9999991488078466 cost= 7.521052753355296e-12
Epoch: 86 w= 1.9999992764866696 cost= 5.43396061571672e-12
Epoch: 87 w= 1.9999993850136693 cost= 3.926036544289031e-12
Epoch: 88 w= 1.999999477261619 cost= 2.8365614029723025e-12
Epoch: 89 w= 1.9999995556723762 cost= 2.0494156128291866e-12
Epoch: 90 w= 1.9999996223215197 cost= 1.480702779721521e-12
Epoch: 91 w= 1.9999996789732917 cost= 1.0698077583047718e-12
Epoch: 92 w= 1.999999727127298 cost= 7.729361059472377e-13
Epoch: 93 w= 1.9999997680582033 cost= 5.584463360924549e-13
Epoch: 94 w= 1.9999998028494728 cost= 4.034774778538369e-13
Epoch: 95 w= 1.9999998324220518 cost= 2.915124779890719e-13
Epoch: 96 w= 1.999999857558744 cost= 2.1061776543919866e-13
Epoch: 97 w= 1.9999998789249325 cost= 1.521713353234463e-13
Epoch: 98 w= 1.9999998970861925 cost= 1.0994378986595627e-13
Epoch: 99 w= 1.9999999125232637 cost= 7.943438830326513e-14
Predict(after training) 4 7.999999650093055

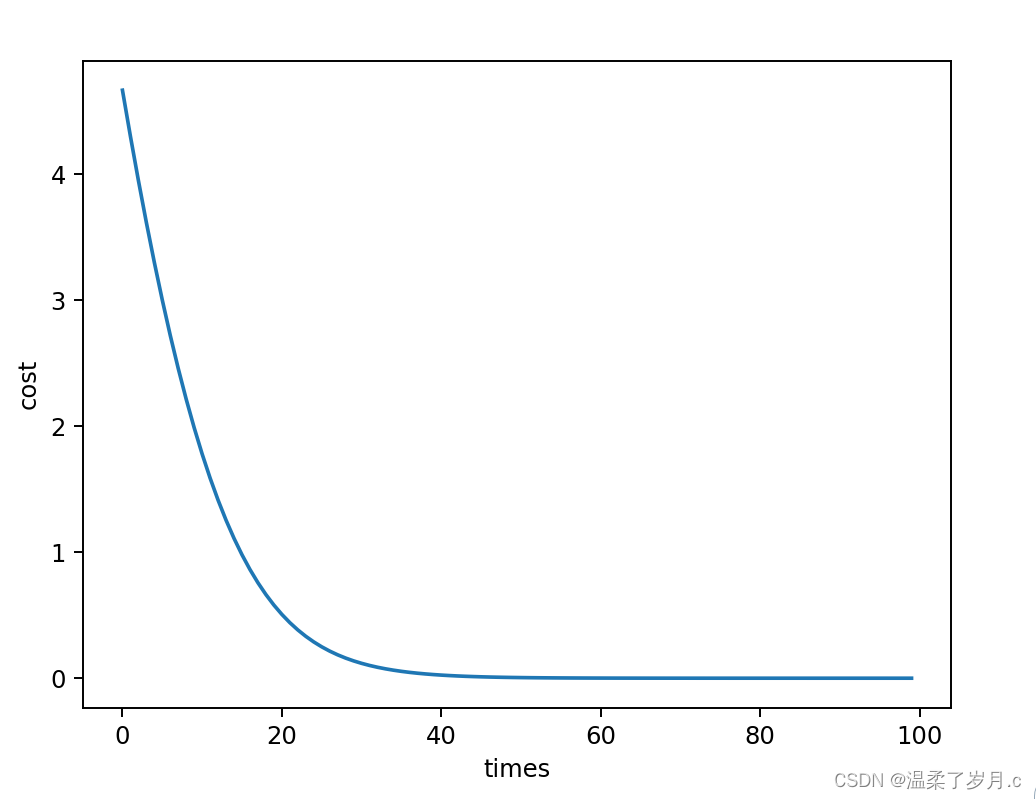
横坐标表示训练的轮数,纵坐标为损失值,通过图分析,随着训练轮数的增加,损失值逐渐减少,趋于0(可能会不等于0)
梯度下降算法存在的问题
使用梯度下降算法,如果遇到鞍点(总体梯度和为0的点),那么就会导致w = w - 学习率 * w中,w 不会改变,就导致w不能够继续更新,为了解决这个问题,就提出了随机梯度下降算法,随机选取一组(x, y)作为梯度下降的依据
随机梯度下降算法
随机梯度下降
#随机梯度算法import numpy as np
import matplotlib.pyplot as pltx_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]w=1.0def forward(x):return w*x#计算MSE
def cost(xs, ys):cost = 0for x, y in zip(xs, ys):y_pred = forward(x)cost += (y_pred - y)**2return cost / len(xs)def gradient(xs, ys):grad = 0for x, y in zip(xs, ys):grad += 2*w*(w*x-y)return grad/len(xs)mse_list = []for epoch in range(100):cost_val = cost(x_data, y_data) #绘图才绘制grad_val = gradient(x_data, y_data) #计算梯度w -= 0.01*grad_valmse_list.append(cost_val)print('Epoch:', epoch, 'w=', w, 'cost=', cost_val)
print('Predict(after training)', 4, forward(4))w_list = np.arange(0, 100, 1)
plt.plot(w_list, mse_list)
plt.ylabel('cost')
plt.xlabel('times')
plt.show()
相关文章:

深度学习之梯度下降算法
梯度下降算法 梯度下降算法数学公式结果 梯度下降算法存在的问题随机梯度下降算法 梯度下降算法 数学公式 这里案例是用梯度下降算法,来计算 y w * x 先计算出梯度,再进行梯度的更新 import numpy as np import matplotlib.pyplot as pltx_data [1.0,…...
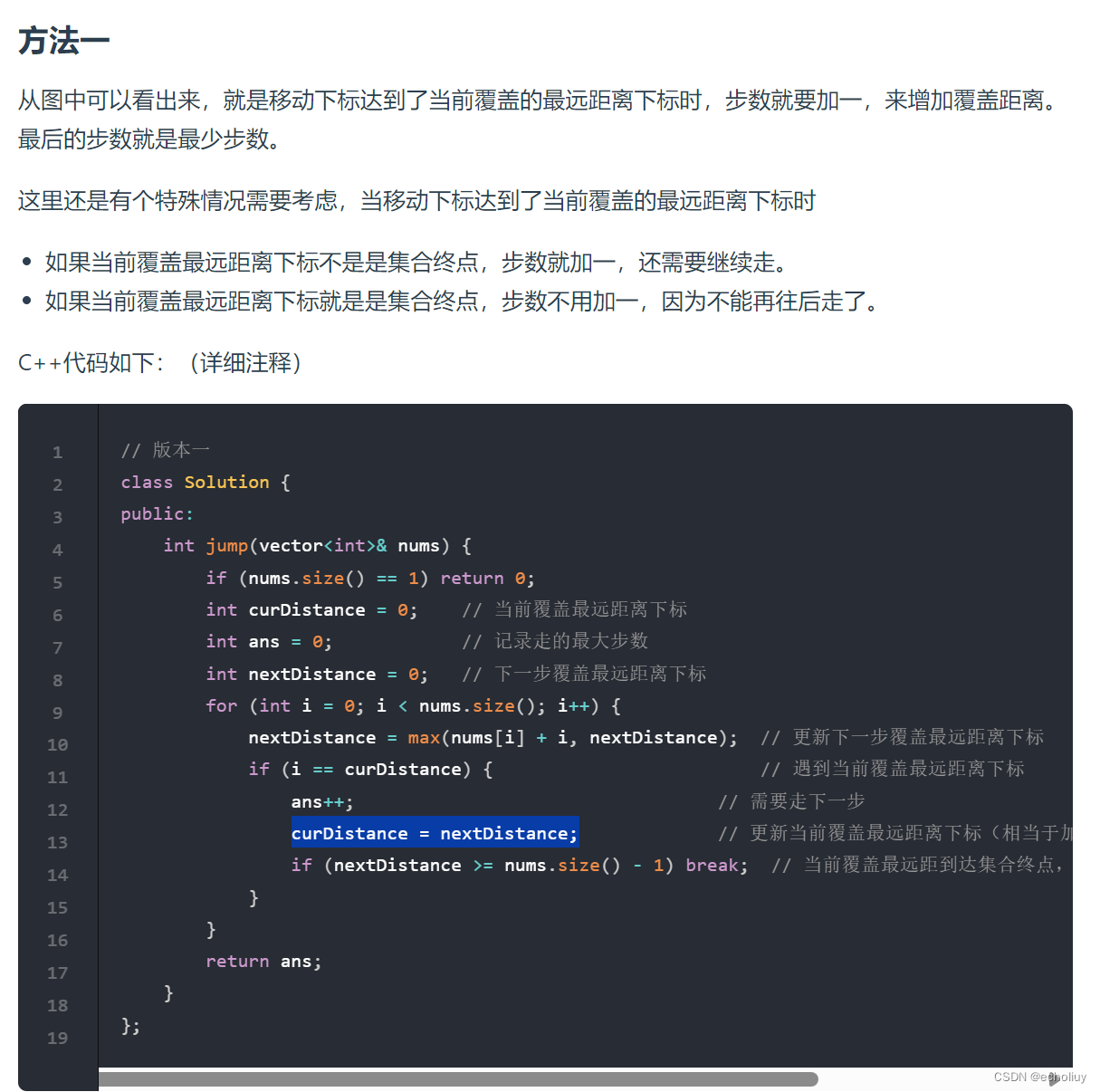
代码随想录第32天|● 122.买卖股票的最佳时机II ● 55. 跳跃游戏 ● 45.跳跃游戏II
文章目录 买卖股票思路一:贪心代码: 思路:动态规划代码: 跳跃游戏思路:贪心找最大范围代码: 跳跃游戏②思路:代码: 方法二:处理方法一的特殊情况 买卖股票 思路一&#x…...
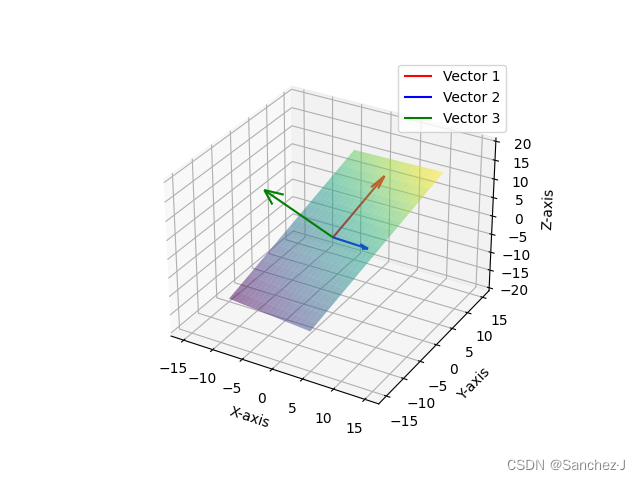
线性代数的本质 2 线性组合、张成的空间、基
基于3Blue1Brown视频的笔记 一种新的看待方式 对于一个向量,比如说,如何看待其中的3和-2? 一开始,我们往往将其看作长度(从向量的首走到尾部,分别在x和y上走的长度)。 在有了数乘后࿰…...

- 工程实践 - 《QPS百万级的有状态服务实践》01 - 存储选型实践
本文属于专栏《构建工业级QPS百万级服务》 《QPS百万级的无状态服务实践》已经完成。截止目前为止,支持需求“给系统传入两个日期,计算间隔有多少天”的QPS百万级服务架构已经完成。如图1: 图1 可是这个架构不能满足需求“给系统传入两个日期…...
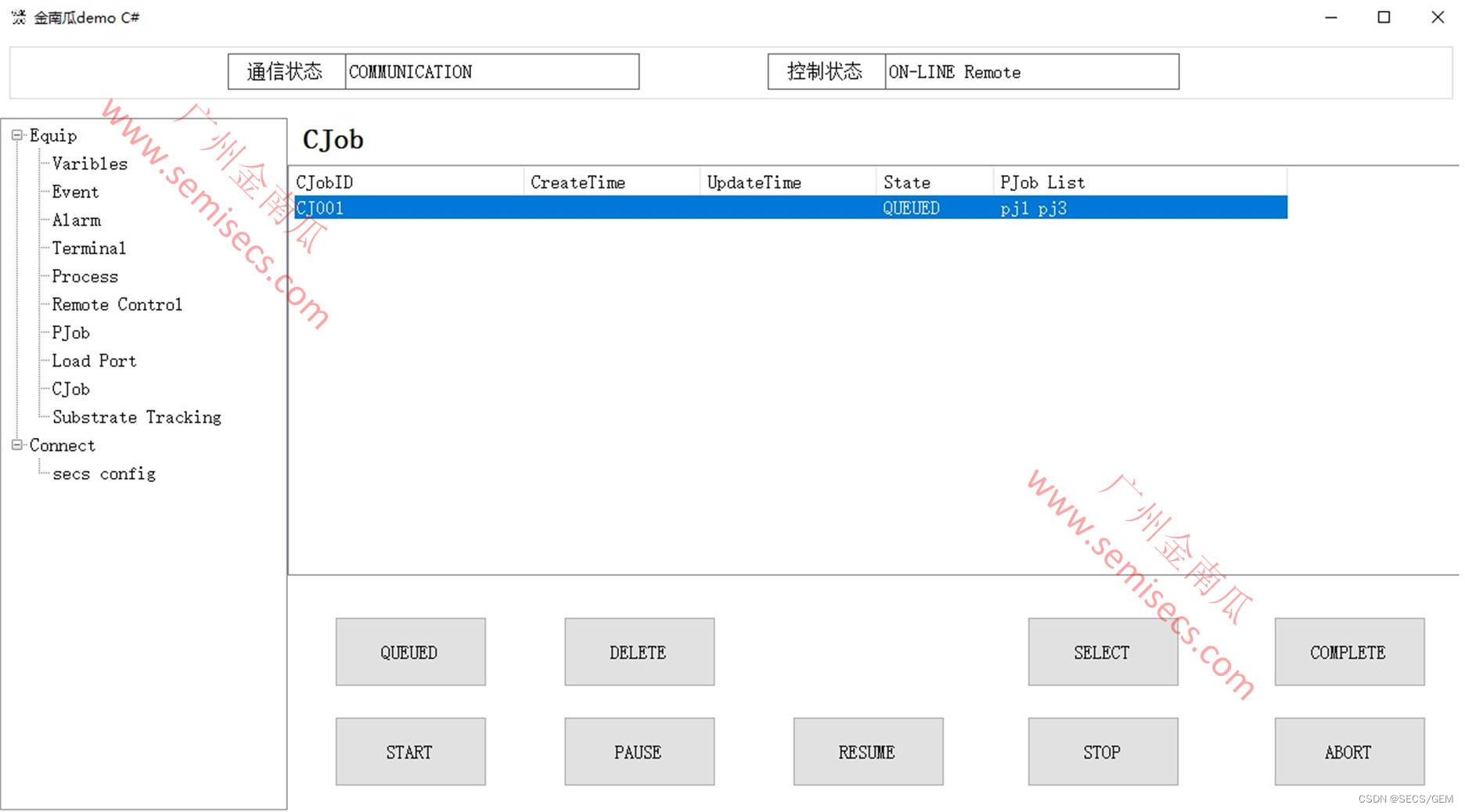
SECS/GEM的HSMS通讯?金南瓜方案
High Speed SECS Message Service (HSMS) 是一种基于 TCP/IP 的协议,它使得 SECS 消息通信更加快速。这通常用作设备间通信的接口。 HSMS 状态逻辑变化(序列): 1.Not Connected:准备初始化 TCP/IP 连接,但尚…...

wayland(xdg_wm_base) + egl + opengles——dma_buf 作为纹理数据源(五)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、EGL dma_buf import 相关的数据结构和函数1. EGLImageKHR2. eglCreateImageKHR()3. glEGLImageTargetTexture2DOES()二、egl 中 import dma_buf 作为纹理的代码实例1. egl_wayland_dmabuf_…...

【VTKExamples::PolyData】第二十八期 LinearExtrusion
很高兴在雪易的CSDN遇见你 VTK技术爱好者 QQ:870202403 前言 本文分享VTK样例LinearExtrusion,并解析接口vtkLinearExtrusionFilter,希望对各位小伙伴有所帮助! 感谢各位小伙伴的点赞+关注,小易会继续努力分享,一起进步! 你的点赞就是我的动力(^U^)ノ~YO 目录…...
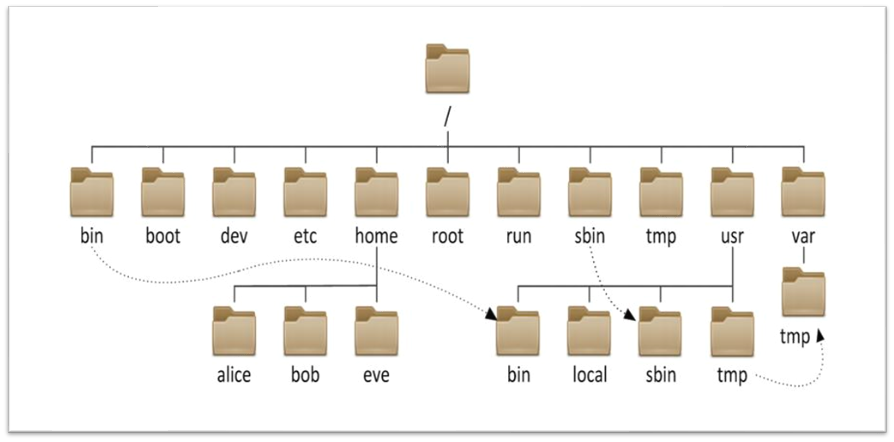
Linux操作系统基础(五):Linux的目录结构
文章目录 Linux的目录结构 一、Linux目录与Windows目录区别 二、常见目录介绍(记住重点) Linux的目录结构 一、Linux目录与Windows目录区别 Linux的目录结构是一个树型结构 Windows 系统 可以拥有多个盘符, 如 C盘、D盘、E盘 Linux 没有盘符 这个概…...

SolidWorks如何在一个零件的基础上绘制另一个零件
经过测试,新建零件,然后插入零件a,在a的基础上绘制b,这种做法无法断开a与b的联系。虽然可以通过切除命令,切除b,但不是正途。 在装配体中可以实现: (1)建立装配体 (2&…...
)
gin(结)
gin day1 今天的目标就是学懂,看懂每一步代码。 gin框架 gin框架就是go语言的web框架。框架你也可以理解成一个库。里面有一堆封装好的工具,帮你实现各种各样的功能,这样使得你可以关注业务本身,而在写代码上少费力。 快速入门&…...

JavaScript 设计模式之桥接模式
桥接模式 通过桥接模式,我们可以将业务逻辑与元素的事件解耦,也可以更灵活的创建一些对象 倘若我们有如下代码 const dom document.getElementById(#test)// 鼠标移入移出事件 // 鼠标移入时改变背景色和字体颜色 dom.onmouseenter function() { th…...

B3651 [语言月赛202208] 数组调整
题目描述 给出一个长度为 n 的数组,第 i 个数为ai。 为了调整这个数组,需要将第 k 个数改变为 −ak。 请你求出调整后的数组中所有数的和。 输入格式 输入共两行。 输入的第一行为两个整数 n,k。 输入的第二行为 n 个整数,第 i 个…...
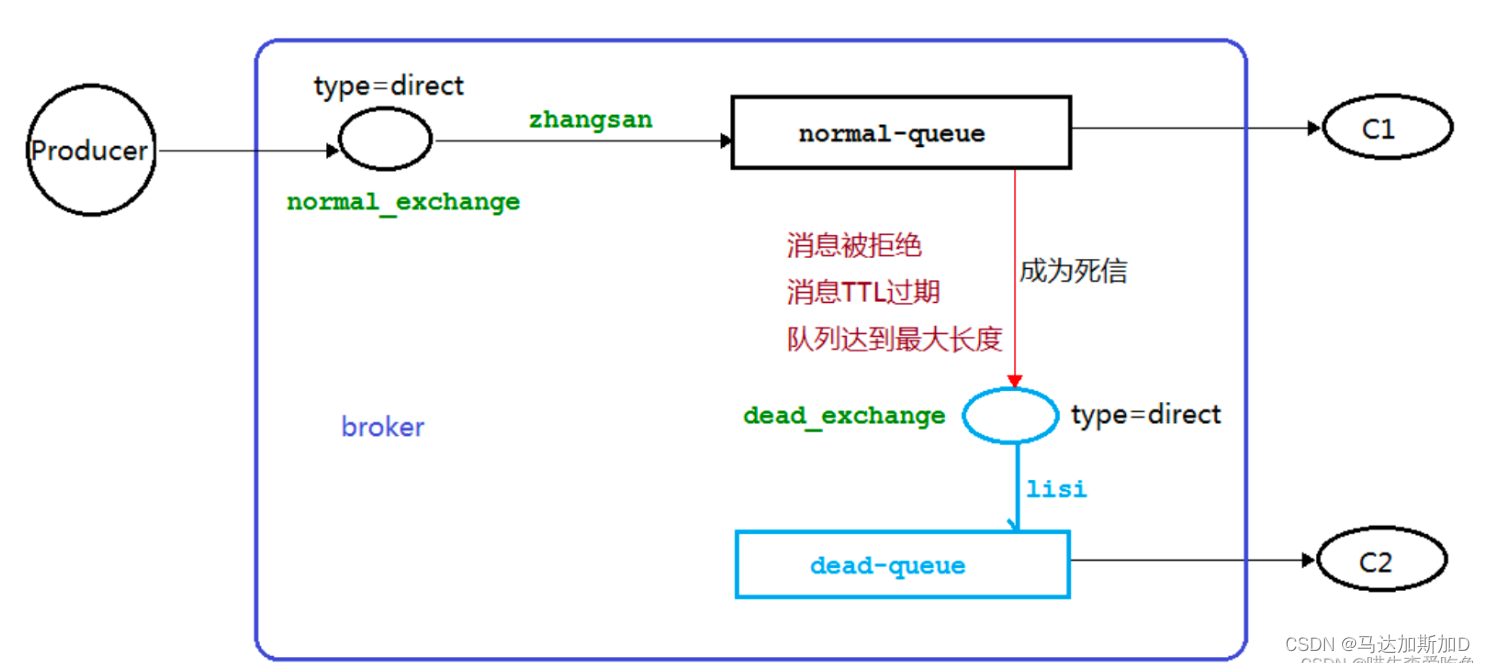
MessageQueue --- RabbitMQ
MessageQueue --- RabbitMQ RabbitMQ IntroRabbitMQ 核心概念RabbitMQ 分发类型Dead letter (死信)保证消息的可靠传递 RabbitMQ Intro 2007年发布,是一个在AMQP(高级消息队列协议)基础上完成的,可复用的企业消息系统,…...
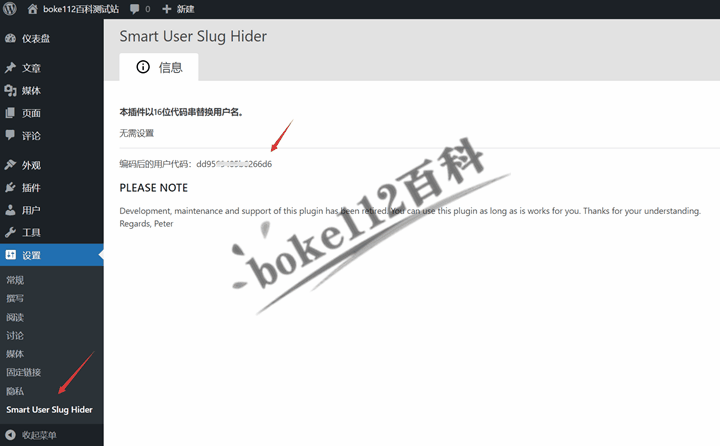
WordPress作者页面链接的用户名自动变成16位字符串串插件Smart User Slug Hider
WordPress默认的作者页面URL链接地址格式为“你的域名/author/admin”,其中admin就是你的用户名,这样的话就会暴露我们的用户名。 为了解决这个问题,前面boke112百科跟大家分享了『如何将WordPress作者存档链接中的用户名改为昵称或ID』一文…...

Nvidia 携手 RTX 推出的本地运行 AI 聊天机器人
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
年假作业day2
1.打印字母图形 #include<stdio.h> #include<string.h> int main(int argc, const char *argv[]) { int i,j; char k; for(i1;i<7;i) { for(j1;j<i;j) { printf("%c",_); } for(j0,…...

HTML-多媒体嵌入-MDN文档学习笔记
HTML-多媒体与嵌入 查看更多学习笔记:GitHub:LoveEmiliaForever MDN中文官网 HTML-中的图片 将图片放入网页 可以使用<img/>来将图片嵌入网页,它是一个空元素,最少只需src属性即可工作 <img src"图片链接"…...

openJudge | 距离排序 C语言
总时间限制: 1000ms 内存限制: 65536kB 描述 给出三维空间中的n个点(不超过10个),求出n个点两两之间的距离,并按距离由大到小依次输出两个点的坐标及它们之间的距离。 输入 输入包括两行,第一行包含一个整数n表示点的个数,第二…...

【教程】MySQL数据库学习笔记(三)——数据定义语言DDL(持续更新)
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【MySQL数据库学习】系列文章 第一章 《认识与环境搭建》 第二章 《数据类型》 第三章 《数据定义语言DDL》 文章目录 【MyS…...
)
[leetcode]买卖股票的最佳时机 (动态规划)
121. 买卖股票的最佳时机 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
