找负环(图论基础)
文章目录
- 负环
- spfa找负环
- 方法一
- 方法二
- 实际效果
负环
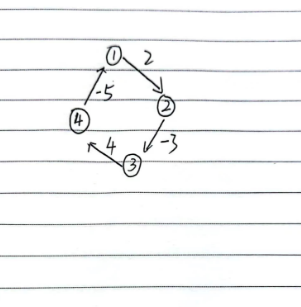
环内路径上的权值和为负。
spfa找负环
两种基本的方法
- 统计每一个点的入队次数,如果一个点入队了n次,则说明存在负环
- 统计当前每个点中的最短路中所包含的边数,如果当前某个点的最短路所包含的边数大于等于n,也说明存在负环
实际上两种方法是等价的,都是判断是否路径包含n条边, n n n条边的话就有 n + 1 n+1 n+1个点
用的更多的还是第二种方法。
方法一
c n t [ x ] : 表示 x 的入队次数 cnt[x]:表示x的入队次数 cnt[x]:表示x的入队次数
#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define inf 0x3f3f3f3f*1llusing namespace std;void solve()
{int n,m1,m2;cin>>n>>m1>>m2;vector<vector<pii>>g(n+1);rep(i,1,m1){int u,v,w;cin>>u>>v>>w;g[u].pb({v,w});g[v].pb({u,w});} rep(i,1,m2){int u,v,w;cin>>u>>v>>w;g[u].pb({v,-w});}vector<int>inq(n+1,0);vector<int>cnt(n+1,0);vector<int>d(n+1,0);queue<int>q;rep(i,1,n){q.push(i);inq[i]=1;}while(q.size()){auto t=q.front();q.pop();int u=t;inq[u]=0;for(auto it:g[u]){int v=it.x,w=it.y;if(d[v]>d[u]+w){d[v]=d[u]+w;if(!inq[v]){q.push(v);inq[v]=1;cnt[v]++;if(cnt[v]>=n){cout<<"YES"<<endl;return;}}}}}cout<<"NO"<<endl;
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
// freopen("1.in", "r", stdin);int _;cin>>_;while(_--)solve();return 0;
}
方法二
c n t [ x ] : 表示从起点到 x 所经过的最短路径的边数 cnt[x]:表示从起点到x所经过的最短路径的边数 cnt[x]:表示从起点到x所经过的最短路径的边数
#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define inf 0x3f3f3f3f*1llusing namespace std;void solve()
{int n,m1,m2;cin>>n>>m1>>m2;vector<vector<pii>>g(n+1);rep(i,1,m1){int u,v,w;cin>>u>>v>>w;g[u].pb({v,w});g[v].pb({u,w});} rep(i,1,m2){int u,v,w;cin>>u>>v>>w;g[u].pb({v,-w});}vector<int>inq(n+1,0);vector<int>cnt(n+1,0);vector<int>d(n+1,0);queue<int>q;rep(i,1,n){q.push(i);inq[i]=1;}while(q.size()){auto t=q.front();q.pop();int u=t;inq[u]=0;for(auto it:g[u]){int v=it.x,w=it.y;if(d[v]>d[u]+w){d[v]=d[u]+w;cnt[v]=cnt[u]+1;if(cnt[v]>=n){cout<<"YES"<<endl;return;}if(!inq[v]){q.push(v);inq[v]=1;}}}}cout<<"NO"<<endl;
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
// freopen("1.in", "r", stdin);int _;cin>>_;while(_--)solve();return 0;
}实际效果


方法一跑出来的结果是 1024 m s 1024ms 1024ms
方法二跑出来的结果是 671 m s 671ms 671ms
相关文章:

找负环(图论基础)
文章目录 负环spfa找负环方法一方法二实际效果 负环 环内路径上的权值和为负。 spfa找负环 两种基本的方法 统计每一个点的入队次数,如果一个点入队了n次,则说明存在负环统计当前每个点中的最短路中所包含的边数,如果当前某个点的最短路所…...
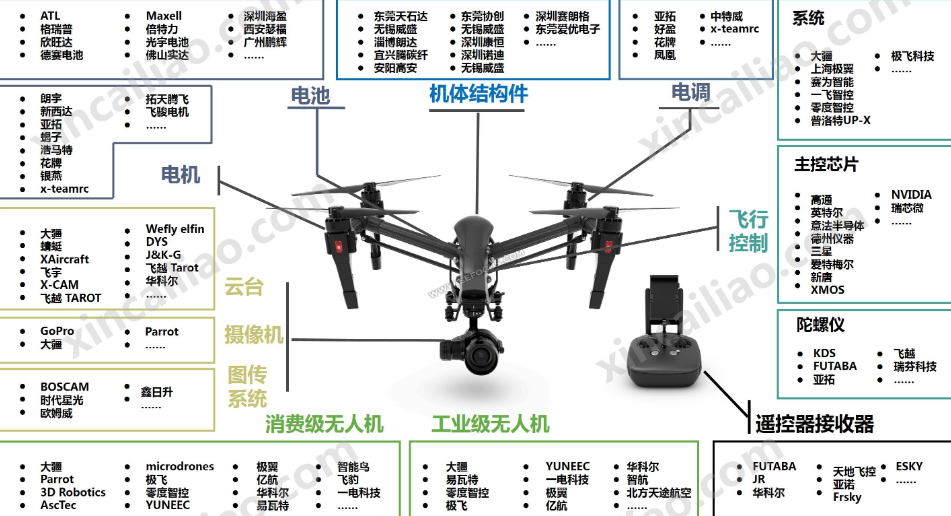
无人机飞控算法原理基础研究,多旋翼无人机的飞行控制算法理论详解,无人机飞控软件架构设计
多旋翼无人机的飞行控制算法主要涉及到自动控制器、捷联式惯性导航系统、卡尔曼滤波算法和飞行控制PID算法等部分。 自动控制器是无人机飞行控制的核心部分,它负责接收来自无人机传感器和其他系统的信息,并根据预设的算法和逻辑,对无人机的姿…...
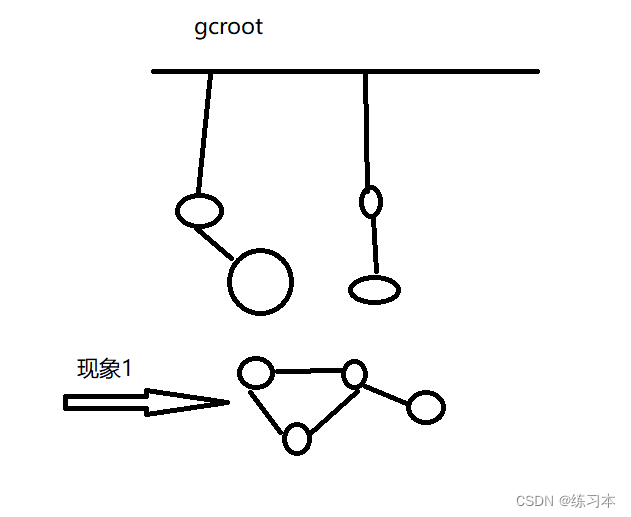
关于内存相关的梳理
1 关键字 总结 (lowmemory,anr in) 2 知识储备 虚拟机原理 垃圾回收算法 又包含标记 和清除两种算法 标记:程序计数器-已过时,可达性分析 具体可见 http://help.eclipse.org/luna/index.jsp?topic%2Forg.ec…...
7.JS里表达式,if条件判断,三元运算符,switch语句,断点调试
表达式和语句的区别 表达式就是可以被求值的代码比如什么a 1 语句就是一段可以执行的代码比如什么if else 直接给B站的黑马程序员的老师引流一波总结的真好 分支语句 就是基本上所有的语言都会有的if else 语句就是满足不同的条件执行不同的代码,让计算机有条件…...
RK3568平台开发系列讲解(存储篇)文件句柄与文件描述符介绍
🚀返回专栏总目录 文章目录 一、什么是文件句柄二、什么是文件描述符2.1、files_struct 结构体2.2、fdtable 结构体三、数据结构关系图沉淀、分享、成长,让自己和他人都能有所收获!😄 一、什么是文件句柄 用户空间的进程通过open系统调用打开一个文件之后,内核返回的就是…...
【C++】类和对象(五)友元、内部类、匿名对象
前言:前面我们说到类和对象是一个十分漫长的荆棘地,今天我们将走到终点,也就是说我们对于C算是正式的入门了。 💖 博主CSDN主页:卫卫卫的个人主页 💞 👉 专栏分类:高质量C学习 &…...
攻防世界 CTF Web方向 引导模式-难度1 —— 1-10题 wp精讲
目录 view_source robots backup cookie disabled_button get_post weak_auth simple_php Training-WWW-Robots view_source 题目描述: X老师让小宁同学查看一个网页的源代码,但小宁同学发现鼠标右键好像不管用了。 不能按右键,按F12 robots …...

Docker之MongoDB安装、创建用户及登录认证
Docker之MongoDB安装、创建用户及登录认证 文章目录 Docker之MongoDB安装、创建用户及登录认证1. 拉取镜像2. 创建宿主机容器数据卷3. 运行mongodb容器1. 运行容器2. 创建用户3. 创建数据库并设置密码 1. 拉取镜像 docker pull mongo:4.2.212. 创建宿主机容器数据卷 运行docke…...
紫微斗数双星组合:天机天梁在辰戌
文章目录 前言内容总结 前言 紫微斗数双星组合:天机天梁在辰戌 内容 紫微斗数双星组合:天机天梁在辰戌 性格分析 在紫微斗数命盘中,天梁星是一颗“荫星”,能够遇难呈祥,化解凶危,主寿,主贵。…...

N-144基于微信小程序在线订餐系统
开发工具:IDEA、微信小程序 服务器:Tomcat9.0, jdk1.8 项目构建:maven 数据库:mysql5.7 前端技术:vue、ElementUI、 Vant Weapp 服务端技术:springbootmybatisredis 本系统分微信小程序和…...

[UI5 常用控件] 09.IconTabBar,IconTabHeader,TabContainer
文章目录 前言1. IconTabBar1.1 简介1.2 基本结构1.3 用法1.3.1 颜色,拖放,溢出1.3.2 Icons Only , Inner Contents1.3.3 showAll,Count,key,IconTabSeparator 1.3.4 Only Text1.3.5 headerMode-Inline1.3.6 design,IconTabSeparator-icon1.3.7 DensityM…...

CCF编程能力等级认证GESP—C++5级—20231209
CCF编程能力等级认证GESP—C5级—20231209 单选题(每题 2 分,共 30 分)判断题(每题 2 分,共 20 分)编程题 (每题 25 分,共 50 分)小杨的幸运数烹饪问题 答案及解析单选题判断题编程题1编程题2 单…...

【论文精读】GPT2
摘要 在单一领域数据集上训练单一任务的模型是当前系统普遍缺乏泛化能力的主要原因,要想使用当前的架构构建出稳健的系统,可能需要多任务学习。但多任务需要多数据集,而继续扩大数据集和目标设计的规模是个难以处理的问题,所以只能…...

10-k8s中pod的探针
一、探针的概念 一般时候,探针的设置,都是为了优化业务时,需要做的事情;属于后期工作; 1,探针的分类 1,健康状态检查探针:livenessProbe 当我们设置了这个探针之后,检查…...
【Langchain Agent研究】SalesGPT项目介绍(二)
【Langchain Agent研究】SalesGPT项目介绍(一)-CSDN博客 上节课,我们介绍了SalesGPT他的业务流程和技术架构,这节课,我们来关注一下他的项目整体结构、poetry工具和一些工程项目相关的设计。 项目整体结构介绍 我们把…...

《UE5_C++多人TPS完整教程》学习笔记4 ——《P5 局域网连接(LAN Connection)》
本文为B站系列教学视频 《UE5_C多人TPS完整教程》 —— 《P5 局域网连接(LAN Connection)》 的学习笔记,该系列教学视频为 Udemy 课程 《Unreal Engine 5 C Multiplayer Shooter》 的中文字幕翻译版,UP主(也是译者&…...
【运维测试】移动测试自动化知识总结第1篇:移动端测试介绍(md文档已分享)
本系列文章md笔记(已分享)主要讨论移动测试相关知识。主要知识点包括:移动测试分类及android环境搭建,adb常用命令,appium环境搭建及使用,pytest框架学习,PO模式,数据驱动࿰…...

高校疫情防控系统的全栈开发实战
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...

OpenTitan- 开源安全芯片横空出世
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
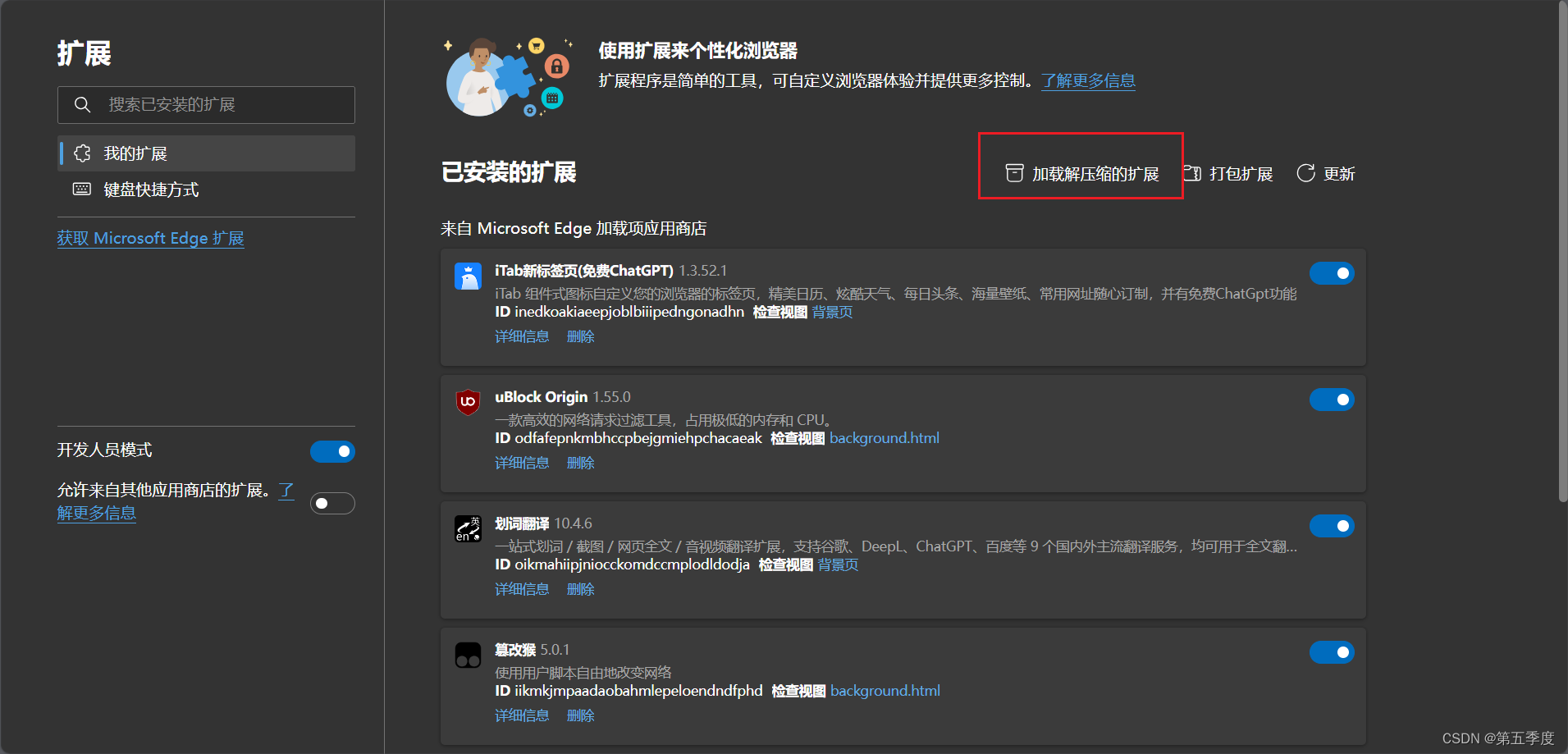
简单的edge浏览器插件开发记录
今天在浏览某些网页的时候,我想要屏蔽掉某些信息或者修改网页中的文本的颜色、背景等等。于是在浏览器的控制台中直接输入JavaScript操作dom完成了我想要的功能。但是每次在网页之间跳转该功能都会消失,我需要反复复制粘贴js脚本,无法实现自动…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
