解决ubuntu登录密码问题
解决ubuntu登录密码问题
不要随便删除密码，不要随便改密码，很容导致密码过期，或者密码无效。参考了很多人的做法，都没有得到解决。下面的过程，够详细了，我就是这么搞好的。
1、重启虚拟机，不停地址按“ESC键”，频率越高越容易出现下面的菜单
2、移动向下光标键，至“Ubuntu 高级选项”
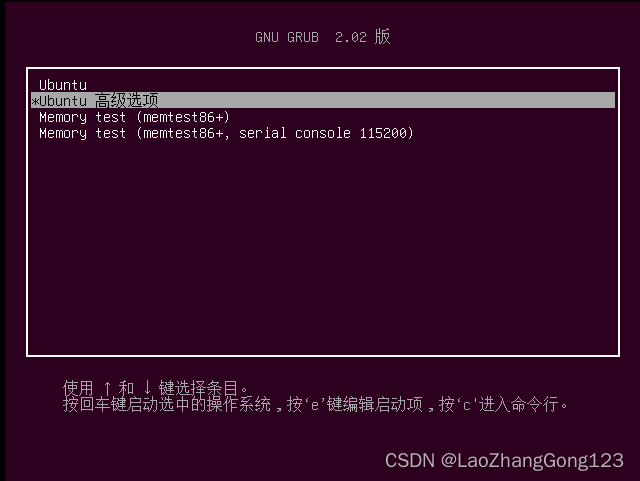
3、按“回车键”，得到下面的界面：
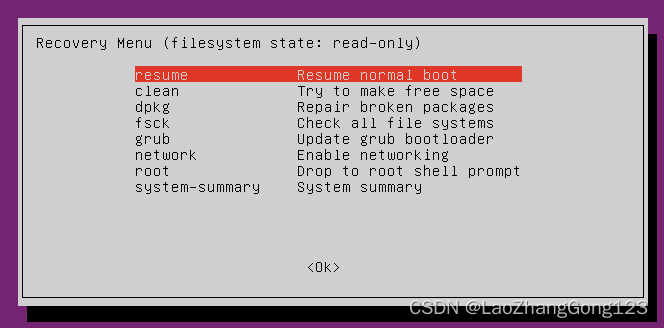
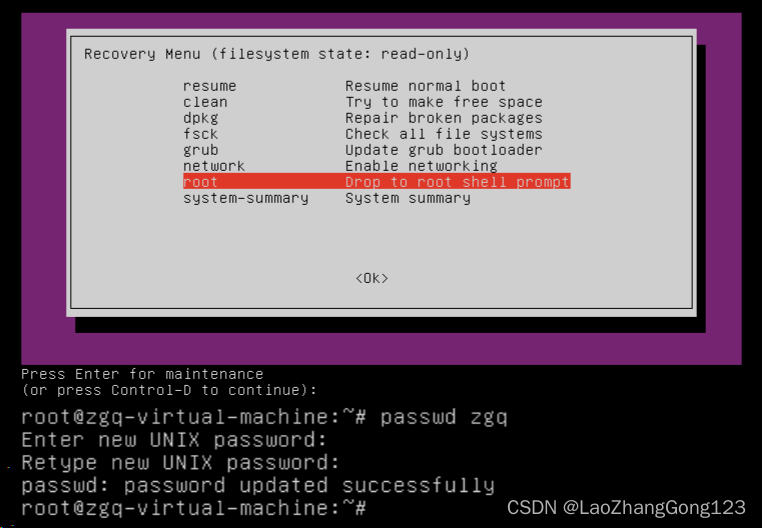
4、移动向下光标键至“root Drop to root shell prompt”，得到下面的界面：
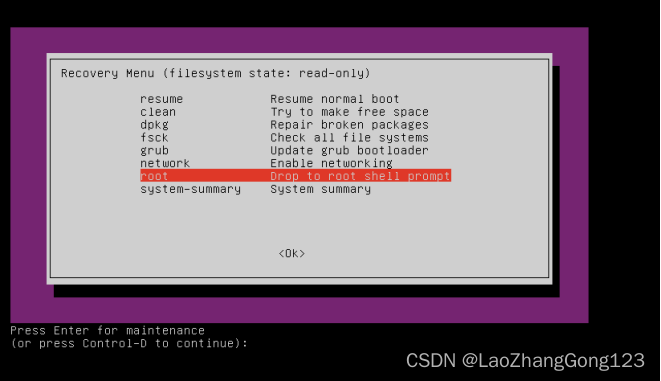
5、输入passwd zgq
这个zgq就是虚拟机用户名
按“回车键”，得到下图：
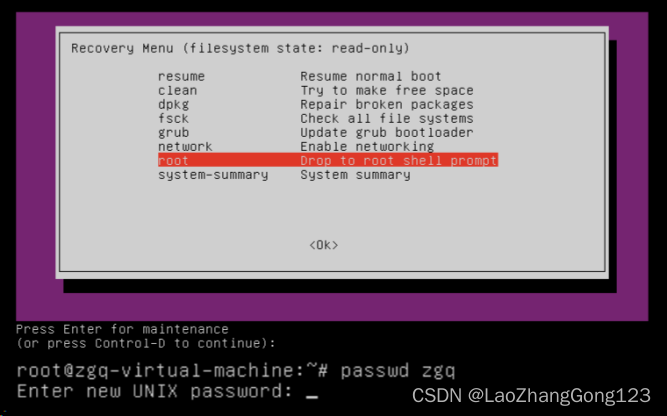
6、在“Enter new UNIX password:”之后，输入新密码123456
按“回车键”
Retype new UNIX password:，输入新密码123456
按“回车键”，出现“passwd: password updated successfully”
7、如果出现“Sorry, passwords do not match”，比如下面的界面，这时，就要重新输入“passwd zgq回车”，再输入密码。没有出现，就跳过这一步。
8、输入“exit”，见下图：
9、按“回车键”，过几分钟，就可以得到下面的界面
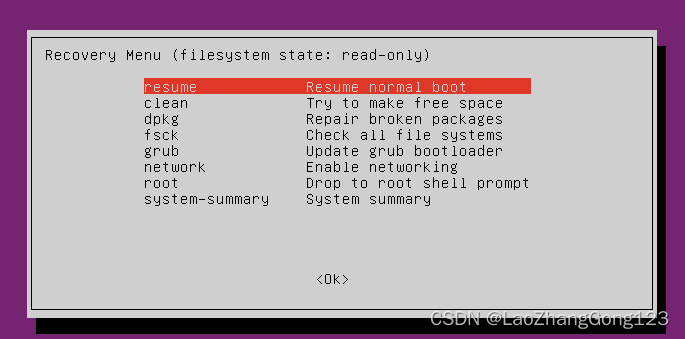
10、按“TAB键”至“Ok”，得到下面的界面：
11、按“回车键”。若还有界面弹出，就执行：
按“TAB键”至“Ok”再按“回车键”，直至虚拟机启动为止。
终于搞好了，差点就要重新安装了。
相关文章：
解决ubuntu登录密码问题
解决ubuntu登录密码问题 不要随便删除密码，不要随便改密码，很容导致密码过期，或者密码无效。参考了很多人的做法，都没有得到解决。下面的过程，够详细了，我就是这么搞好的。 1、重启虚拟机，不停…...
Ubuntu忘记登录密码重置步骤
Ubuntu忘记登录密码重置步骤 1.开机界面长按shitf键，进入grub，并选择Advanced options for ubuntu，按下回车 2.选择一个较新版本的recovery mode，按下回车 3.会跑一些数据，等待跑完后会出现下面的界面，选择…...
MySQL数据库基础（五）：SQL语言讲解
文章目录 SQL语言讲解 一、SQL概述 二、SQL语句分类 1、DDL 2、DML 3、DQL 4、DCL 三、SQL基本语法 1、SQL语句可以单行或多行书写，以分号结尾 2、可使用空格和缩进来增强语句的可读性 3、MySQL数据库的SQL语句不区分大小写，关键字建议使用大写…...
python-使用ffmpeg批量修改文件的后缀名
import os import subprocessdef convert_ogg_to_mp3(directory):for filename in os.listdir(directory):if filename.endswith(".ogg"):# 获取文件的完整路径file_path os.path.join(directory, filename)# 创建一个新的文件名，只是将扩展名从.ogg更改…...
关于jupyter的一些小笔记
关于jupyter的一些小笔记 1.Jupyter Notebook：单/多行注释，组合键：选中代码，按Ctrl /。 2.安装PHATE包 使用pip直接进行安装 pip install --user phate成功解决AttributeError: module ‘numpy’ has no attribute ‘float’. 报…...
macOS 安装 conda
macOS 安装 conda 安装 conda参考 Conda是一个开源的软件包管理系统和环境管理系统，用于安装和管理软件包和其依赖项。 安装 conda mkdir miniconda3 cd miniconda3 bash Miniconda3-latest-MacOSX-x86_64.sh$ conda list参考 macOS 安装 conda开始使用conda...
C++并发编程 -3.同步并发操作
本文介绍如何使用条件变量控制并发的同步操作、C 并发三剑客，函数式编程 一.条件变量 1.概念 C条件变量（condition variable）是一种多线程编程中常用的同步机制，用于线程间的通信和协调。它允许一个或多个线程等待某个条件的发生…...
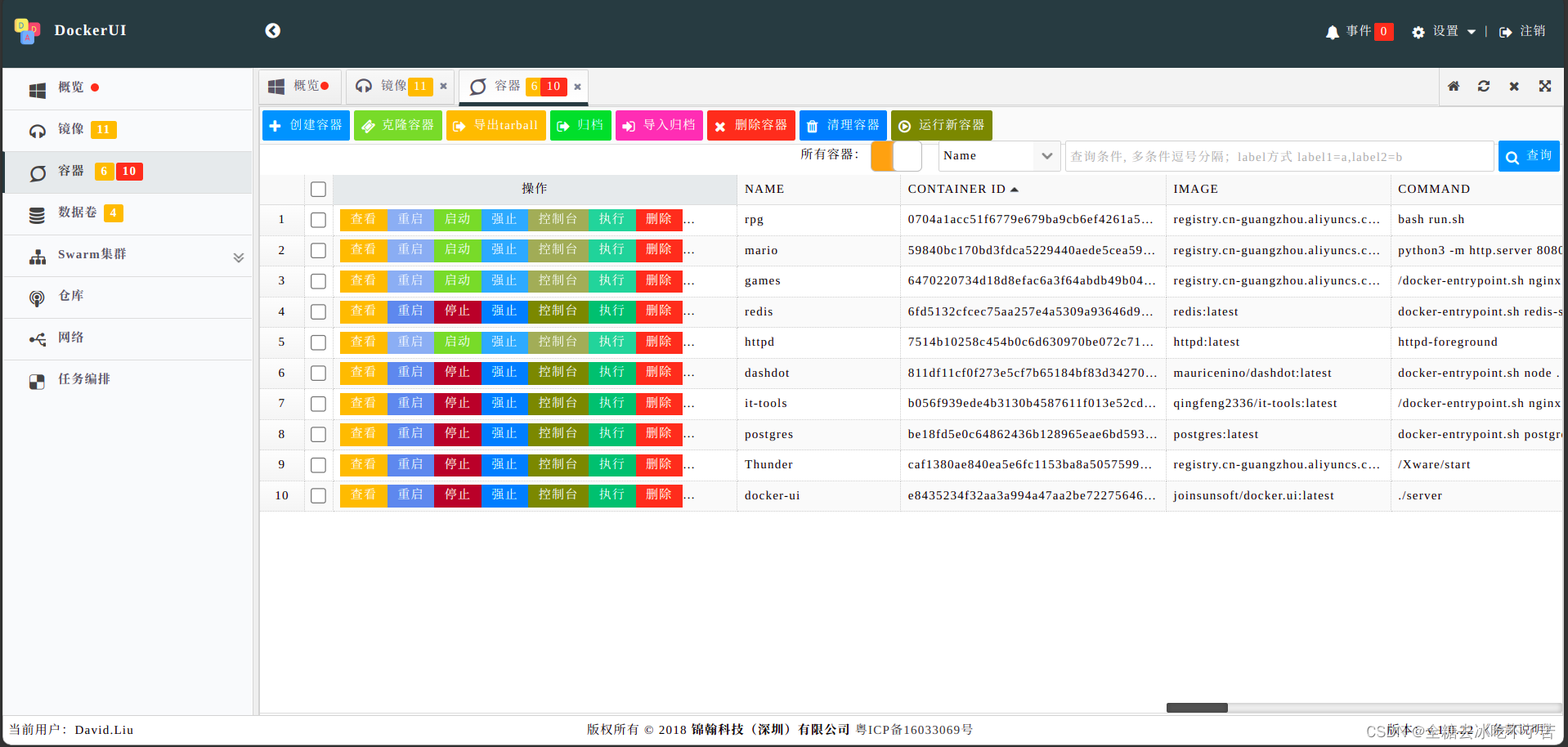
【打工日常】使用docker部署可视化工具docker-ui
一、docker-ui介绍 docker-ui是一个易用且轻量化的Docker管理工具，透过Web界面的操作，方便快捷操作docker容器化工作。 docker-ui拥有易操作化化界面，不须记忆docker指令，仅需下载镜像即可立刻加入完成部署。基于docker的特性&…...
LGAMEFI基于BPL公链开发的第一生态：开启RWA游戏娱乐与DeFi融合的新纪元
在去中心化金融（DeFi）与游戏娱乐的结合趋势中，BPL公链上的LGAMEFI项目代表了前沿的技术革新和市场领导。这种将web2上成熟页游进行RWA链改，不仅仅是将游戏热门领域融合，更是在寻找一种全新的参与者经验，将玩…...
AI专题：5G-A扬帆风正劲，踏AI增长新浪潮
今天分享的是AI系列深度研究报告：《AI专题：5G-A扬帆风正劲，踏AI增长新浪潮》。 （报告出品方：开源证券） 报告共计：22页 足立连接，拓展算力，双曲线稳步发力 中兴通讯拥…...
C++Linux网络编程：poll模型和简单使用
文章目录 poll模型pollfd结构体nfds_t的定义 一个简单的poll服务器总结 poll模型 poll模型和select模型类似，都是在指定时间内轮询一定数量的文件描述符，以测试其中是否有就绪者，需要使用头文件poll.h： #include <poll.h>…...
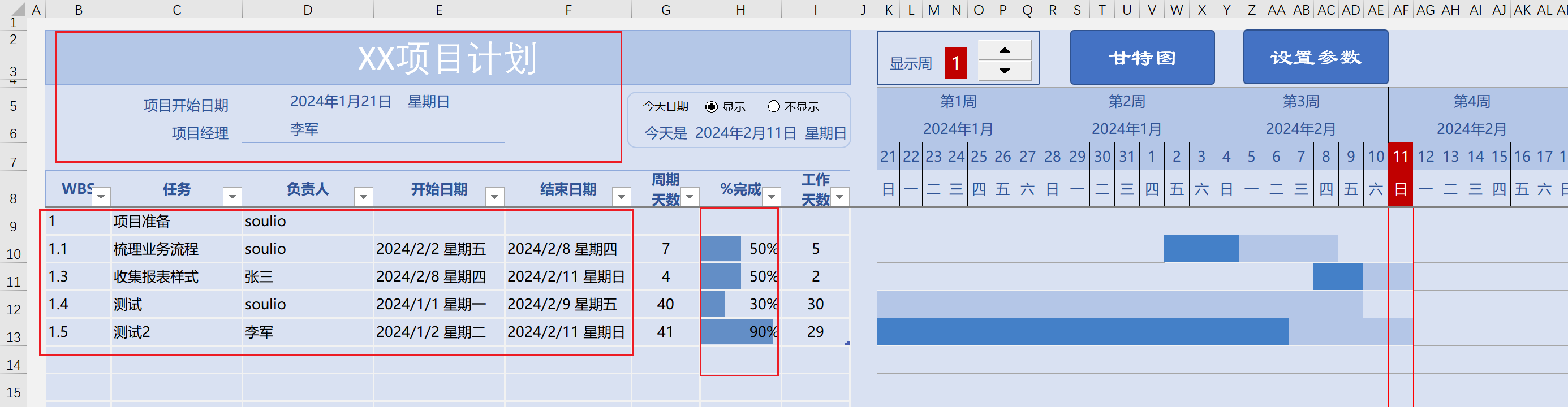
Excel模板2：进度条甘特图
Excel模板2：进度条甘特图 今天复刻B站up【名字叫麦兜的狗狗】的甘特图：还在买Excel模板吗？自己做漂亮简洁的甘特图吧！_哔哩哔哩_bilibili 阿里网盘永久分享：https://www.alipan.com/s/cXhq1PNJfdm 当前效果&…...
数据结构:4_二叉树
二叉树 一.树概念及结构 1. 树的概念 树是一种非线性的数据结构，它是由n（n>0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。 有一个**特殊的…...
设计模式之：状态模式（State Pattern）
状态模式（State Pattern） 状态模式是一种行为设计模式，允许一个对象在其内部状态改变时改变它的行为。这种模式通过把状态的变化逻辑分布到State的子类之间，减少了相互间的依赖，使得状态的切换更加清晰。 状态模式的…...
【微服安全】API密钥和令牌与微服务安全的关系
什么是 API 密钥和令牌 API 密钥 API 密钥是一串用于识别应用程序或用户的字符串。它通常用于授权应用程序或用户访问 API。API 密钥可以是公开的，也可以是私有的。公开的 API 密钥可供任何人使用，而私有的 API 密钥只能由授权的应用程序或用户使用。 …...
Mock.js
在开发后端的应用中，我们使用postman来测试接口，观察和验证前后端之间的数据传递是否正常。 在开发前端的应用中，我们使用Mock.js来模拟后端服务，以便进行前端业务逻辑的开发和测试。 一般情况下，个人开发或者小团队开…...
【c++】list详细讲解
> 作者简介：დ旧言~，目前大二，现在学习Java，c，c，Python等 > 座右铭：松树千年终是朽，槿花一日自为荣。 > 目标：熟悉list库 > 毒鸡汤：你的脸上云淡…...
C#面：在.NET中 类 System.Web.UI.Page 可以被继承吗？
可以。 它是 ASP.NET WebForms中的一个重要类，用于表示 Web 页面。通过继承 System.Web.UI.Page 类，可以创建自定义的 Web 页面，并在其中添加自己的逻辑和功能。 继承 System.Web.UI.Page 类的好处是，可以重用和扩展已有的功能。…...
AI：128-基于机器学习的建筑物能源消耗预测
🚀点击这里跳转到本专栏，可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航！ 从基础到实践，深入学习。无论你是初学者还是经验丰富的老手，对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带有在本地跑过的关键代码，详细讲解供…...
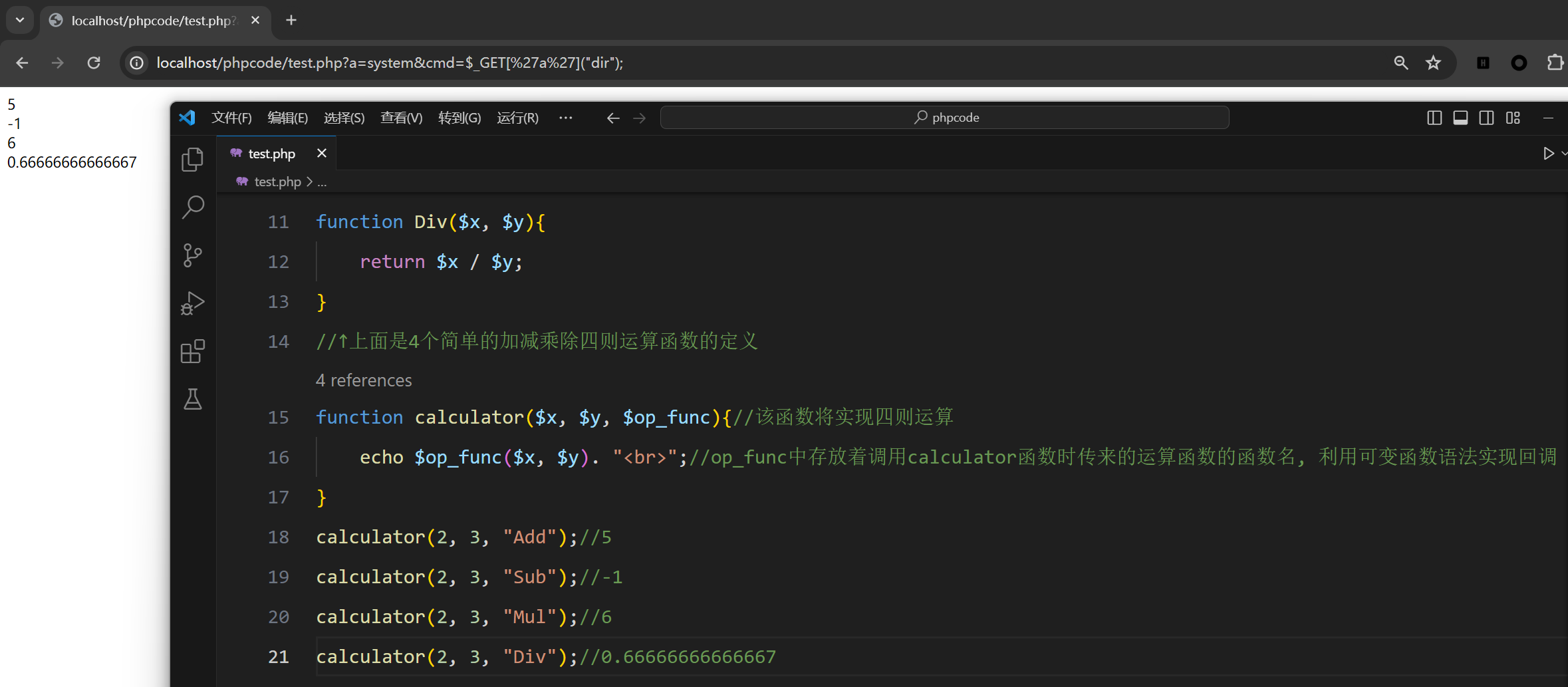
php基础学习之可变函数（web渗透测试关键字绕过rce和回调函数）
可变函数 看可变函数的知识点之前，蒟蒻博主建议你先去看看php的可变变量，会更加方便理解，在本篇博客中的第五块知识点->php基础学习之变量-CSDN博客 描述 当一个变量所保存的值刚好是一个函数的名字（由函数命名规则可知该值必…...
Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
19c补丁后oracle属主变化，导致不能识别磁盘组
补丁后服务器重启，数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后，存在与用户组权限相关的问题。具体表现为，Oracle 实例的运行用户（oracle）和集…...
【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1：执行计划绑定问题？尝试：SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库，并对 SQL 进行优化了，添加了强制索引。 UAT 环境已经生效，但 PROD 环境强制索…...
大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动（如演唱会、马拉松赛事、高考中考等）期间，城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例，暖城商圈曾因观众集中离场导致周边…...
ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++，无法导入ardupilot代码，会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入（联动）2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展，人们对手机的需求越来越大，各种手机软件也都在被广泛应用，但是对于手机进行数据信息管理，对于手机的各种软件也是备受用户的喜爱，社区养老保险系统小程序被用户普遍使用，为方…...
使用LangGraph和LangSmith构建多智能体人工智能系统
现在，通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战，比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存，但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程，可以参考这篇文章，我觉得写的非常…...
篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...