DS:八大排序之直接插入排序、希尔排序和选择排序
创作不易,感谢三连支持!!
一、排序的概念及运用
1.1 排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起 来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记 录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列 r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据 的排序。
关于这些基础概念我会在后面慢慢介绍!
1.2 排序的运用
我们在淘宝购买商品的时候,可以选择让商品根据销量、信用、价格、综合程度进行排序
还有高校排名,以及考试的排名,都是通过排序来完成的!!
排序存在的意义:帮助我们筛选出最优的选择
1.3 常见的排序算法
二、直接插入排序
2.1 思路
直接插入排序的思想:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
这就和我们小时候玩扑克牌摸牌整理的一样,一次与前面的排比较找到合适的位置插入!

2.2 直接插入排序的实现
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
我们先按照上面的思路,先模拟摸一张牌的过程,假设目前手上的牌是2 4 9 然后摸到了1张3,我们设置最后一张牌9的下标位置为end(2),然后让新摸的牌为temp(a[3]),开始慢慢往前比较,发现较大的就交换位置。
int end=2;int temp=a[3];while (end >= 0){if (a[end] > temp)//如果前面的数比后面的数大,就前面元素插入到后面的位置{ a[end + 1] = a[end];--end;}elsebreak;}a[end+1] = temp;//不写在循环里面,是避免end减成-1,此时说明新加入的牌是最小的,正好放在一开始的位置
上述过程可以实现插入一张牌,那么整体的实现就在外面加个for循序即可!!
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int temp = a[i+1];while (end >= 0){if (a[end] > temp)//如果前面的数比后面的数大,就前面元素插入到后面的位置a[end + 1] = a[end];elsebreak;--end;}a[end + 1] = temp;//不写在循环里面,是避免end减成-1,此时说明新加入的牌是最小的,正好放在一开始的位置}
}但要注意的是:外面的for循环的判断条件,i < n - 1, 也就是说i最多走到n - 2的位置即倒数第二个元素,原因是:tmp是每次要插入的元素,而tmp = a[end +1]是end的下一个位置,如果让end到最后一个元素的位置即n-1处,那tmp = a[end+1]就会越界!所以i只能到倒数第二个元素的位置!
2.3 复杂度分析
时间复杂度:O(N^2) ---> 单趟是O(N),最坏情况N个元素都要走一次单趟(基本上逆序)
空间复杂度:O(1) ---> 额外使用空间的个数是常数个
当要排序的序列接近有序时性能最好O(N)(接近有序)
三、希尔排序
3.1 思路
希尔排序其实是直接插入排序的一种变形,我们知道对于直接插入排序来说,最坏的情况就是逆序,此时的时间复杂度就是O(N^2),最好的情况是接近有序,此时时间复杂度为O(N),这个时候希尔有了一个想法:有没有一种方法可以让一组无序的数据经过处理后使他接近有序,然后再最后实现一次直接插入排序呢?
最后希尔发明出来了希尔排序
3.2 希尔排序的实现
具体思路:
1、对无序的数组进行预排序,使其接近有序。
2、最后再来一次直接插入排序
这里的预排指的是:间隔gap的元素为一组,总计gap组,我们先假设gap为3,然后我们画个图来理解一下:

根据我们之前写的直接插入排序算法,我们可以先实现将红色的一组进行排序的算法
int gap = 3;
for (int i = 0; i < n - gap; i+=gap)
{int end = i;int temp = a[i + gap];while (end >= 0){if (a[end] > temp)//如果前面的数比后面的数大,就前面元素插入到后面的位置a[end + gap] = a[end];elsebreak;end -= gap;}a[end + gap] = temp;
}我们发现,如果我们一开始让i=1,就可以实现蓝色组的排序,让i=2的话,就可以实现绿色组的排序,所以为了让三组都完成排序,我们再外面再嵌套一层循环!
int gap = 3;
for (int j = 0; j < gap; j++)
{for (int i = j; i < n - gap; i += gap){int end = i;int temp = a[i + gap];while (end >= 0){if (a[end] > temp)//如果前面的数比后面的数大,就前面元素插入到后面的位置a[end + gap] = a[end];elsebreak;end -= gap;}a[end + gap] = temp;}
}这样我们就实现了三组的预排序了!!
但其实上面的代码还可以优化成两层循环!!
int gap = 3;for (int i = 0; i < n - gap; i ++){int end = i;int temp = a[i + gap];while (end >= 0){if (a[end] > temp)//如果前面的数比后面的数大,就前面元素插入到后面的位置a[end + gap] = a[end];elsebreak;end -= gap;}a[end + gap] = temp;}刚刚那种写法是一组一组去完成预排,而现在这种写法是实现多组并排,效果是一样的!!
这样的预排序有什么意义呢?
1、 gap越大,大的数可以更快到后面,小的数可以更快到前面,但是越不接近有序
2、gap越小,大的小的就挪动的越慢,但是也越接近有序
3、gap==1时,就是直接插入排序(我们可以发现当gap等于1时,这个预排序算法与直接插入排序算法的写法是一样的!!)
现在来分析gap该取多少合适?
首先,gap是不能随便取的,因为比如说有100万个数据,gap取3,显然是不合适的,所以我们的gap一定要跟数据个数n建立联系,gap具体取多少是最合适的没有得到很好的证明,所以我们使用Knuth的思路来将我们的希尔排序完善好!!

void ShellSort(int* a, int n)
{//gap>1 预排序//gap=1 直接插入排序int gap = n;while (gap > 1){gap = gap / 3 + 1;//这是为了保证gap最后一定为0for (int i = 0; i < n - gap; i++){int end = i;int temp = a[i + gap];while (end >= 0){if (a[end] > temp)//如果前面的数比后面的数大,就前面元素插入到后面的位置a[end + gap] = a[end];elsebreak;end -= gap;}a[end + gap] = temp;}}
}需要注意的是:gap = gap / 3 + 1是为了保证gap最后一定会等于1,也就是一定会在最后进行一次直接插入排序,保证有序,而前面gap>1的过程都是在进行预排序!!
3.3 复杂度分析
 因为预排是一个逐渐转好的过程,所以我们还按照最坏情况去考虑是不合理的,因此这边是难以计算的,我们看看书上的讲解
因为预排是一个逐渐转好的过程,所以我们还按照最坏情况去考虑是不合理的,因此这边是难以计算的,我们看看书上的讲解
《数据结构(C语言版)》--- 严蔚敏
《数据结构-用面相对象方法与C++描述》--- 殷人昆

因为咋们的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时就按o(N^1.25)到o(1.6N^1.25)到来算
四、选择排序
4.1 思路
选择排序的思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
这个其实也跟摸扑克牌有关,但是这次跟直接插入排序不一样的是,直接插入排序是一次摸一张牌然后插入调整,而选择排序是一次性拿了所有牌,再逐个把小的数往前放!
4.2 选择排序的实现
1、在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
2、若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
3、在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
我们拿到所有的牌后,每次都把最小的牌往前放
void SelectSort(int* a, int n)
{for (int begin = 0; begin < n; begin++){int min = begin;//记录最小元素的下标for (int i = begin+1; i < n; i++){if (a[min] > a[i])min = i;//记录最小的牌的下标}Swap(&a[begin], &a[min]);}
}但是每次遍历就记一张最小的牌,效率太低下了,所以我们改造一下该算法,使得该算法每遍历一次就记住最小的牌和最大的牌,然后分别放在两边!!
void SelectSort(int* a, int n)
{int left = 0; int right = n - 1;while (left < right){int min = left;int max = left;for (int i = left+1; i <= right; i++){if (a[min] > a[i])min = i;if (a[max] < a[i])max = i;}//这里要考虑一种情况,就是如果最大的数恰好就在最左端,那么就会导致第二次swap换到后面的就不是最大的数而是最小的数了Swap(&a[min], &a[left]);//如果max和begin重叠,修正一下if (max == left)max = min;Swap(&a[max], &a[right]);left++;right--;}
}易错点1:min和max要从他们后面的第一张牌开始去一张一张比较
易错点2:交换的时候,如果最大的元素恰好在最左边,那么就有可能被最小的元素给交换过去了,所以这个时候要注意及时地修正!!
4.3 复杂度分析
时间复杂度:O(N^2)
单趟无论选择一个还是选择两个,都得遍历一遍,复杂度为O(N),整体还得遍历一遍O(N)
空间复杂度:O(1)
相关文章:

DS:八大排序之直接插入排序、希尔排序和选择排序
创作不易,感谢三连支持!! 一、排序的概念及运用 1.1 排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起 来的操作。稳定性&…...
)
【MySQL】-21 MySQL综合-8(MySQL默认值+MySQL非空约束+MySQL查看表中的约束)
MySQL默认值MySQL非空约束MySQL查看表中的约束 MySQL默认值在创建表时设置默认值约束在修改表MySQL默认值在创建表时设置默认值约束在修改表时添加默认值约束删除默认值约束删除默认值约束 MySQL非空约束在创建表时设置非空约束在修改表时添加非空约束删除非空约束 MySQL查看表…...

力扣hot3--并查集+哈希
第一想法是排个序然后遍历一遍,but时间复杂度就超啦 并查集居然与哈希结合了() 已经好久没用过并查集了,,,我们用哈希表f_node中来记录原结点的父节点,其中key是原结点,value是父节点…...
微信网页版能够使用(会顶掉微信app的登陆)
一、文件结构 新建目录chrome新建icons,其中图片你自己找吧新建文件manifest.json新建文件wx-rules.json 二、文件内容 对应的png你们自己改下 1、manifest.json {"manifest_version": 3,"name": "wechat-need-web","author…...
会影响word文档中插入图片的分辨率吗?)
word软件中硬件图像加速有什么用处?禁用硬件图形加速(G)会影响word文档中插入图片的分辨率吗?
问题描述:word软件中硬件图像加速有什么用处?禁用硬件图形加速(G)会影响word文档中插入图片的分辨率吗? 问题解答: 在 Microsoft Word 中,硬件图形加速主要用于提高图形元素的渲染速度和性能,特别是处理大…...
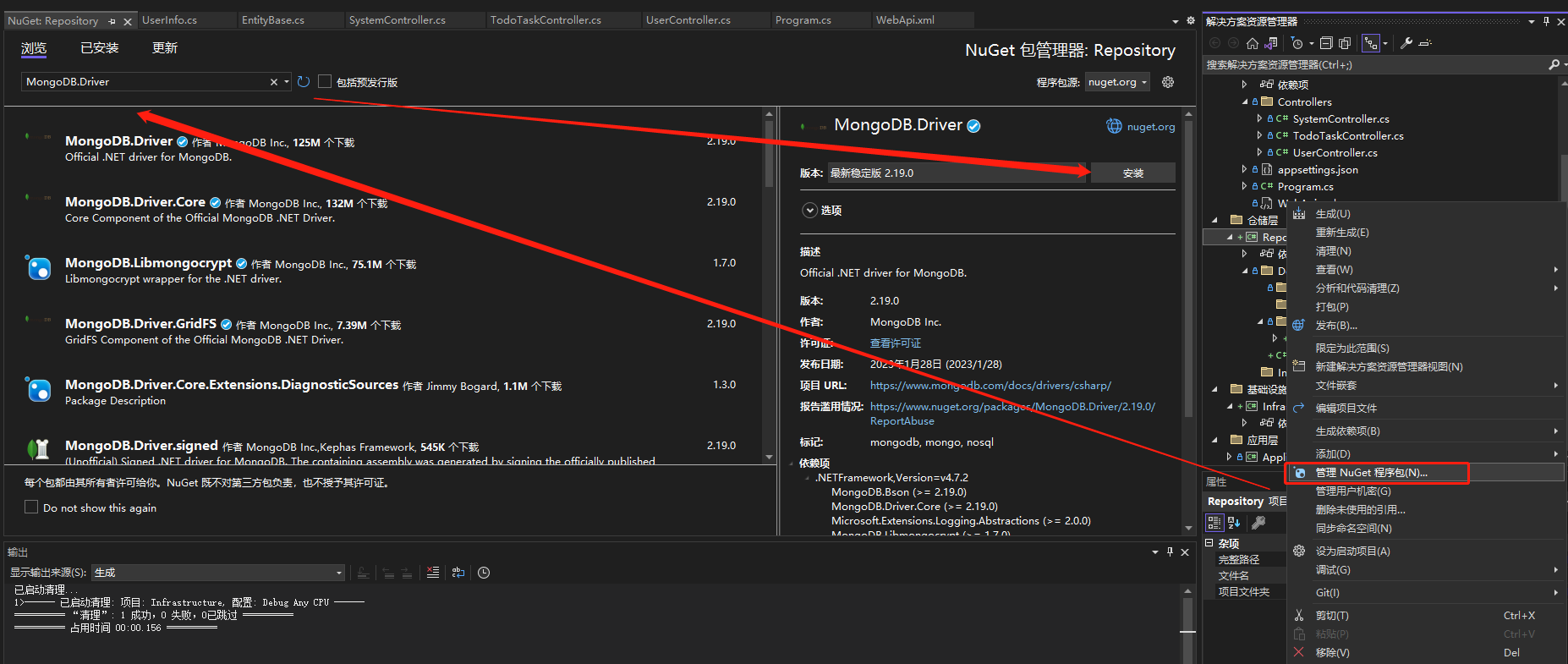
.NET Core MongoDB数据仓储和工作单元模式封装
前言 上一章我们把系统所需要的MongoDB集合设计好了,这一章我们的主要任务是使用.NET Core应用程序连接MongoDB并且封装MongoDB数据仓储和工作单元模式,因为本章内容涵盖的有点多关于仓储和工作单元的使用就放到下一章节中讲解了。仓储模式(R…...

lua:有关表访问的metamethod
针对在两种正常状态:表的不存在的域的查询和修改,Lua也提供了改变 tables的行为的方法。 index metamethod 我们可以通过index元方法来实现访问table内部不存在的域时人为操控返回数据。 比如以下测试代码: local set {1,2,3} setmetata…...
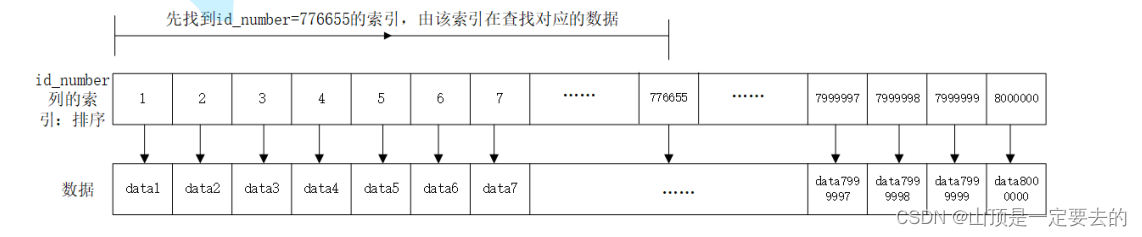
【MySQL】索引事务
MySQL索引事务 1. 索引1.1 概念1.2 作用1.3 使用场景1.4 使用1.5 案例 2. 事务2.2 事物的概念2.3 使用 3. 内容重点总结 1. 索引 1.1 概念 索引是一种特殊的文件,包含着对数据表里所有记录的引用指针。可以对表中的一列或多列创建索引, 并指定索引的类…...

ChatGPT重大升级:能自动记住用户的习惯和喜好,用户有权决定是否共享数据给OpenAI
OpenAI刚刚宣布了ChatGPT的一项激动人心的更新! OpenAI在ChatGPT中新加了记忆功能和用户控制选项,这意味着GPT能够在与用户的互动中记住之前的对话内容,并利用这些信息在后续的交谈中提供更加相关和定制化的回答。 这一功能目前正处于测试阶…...

CSS设置盒子阴影
语法 box-shadow: *h-shadow v-shadow blur spread color* inset; 注释: box-shadow向框添加一个或多个阴影. 该属性是由逗号分隔的阴影列表,每个阴影由2-4个长度值、可选的颜色值及可选的inset关键词来规定。省略长度的值是0。 外阴影 a、给元素右边框和下边框加外阴影——把…...
文件夹删不掉,显示在另一个文件中打开怎么办
问题: 一、想要删掉这个文件夹,却因为文件夹中的文件打开了删不掉,这里我因为做的测试,所以是知道打开了什么 二、一般情况下文件比较多时,是不知道打开了什么的,长这个样子 解决: 一、打开任…...
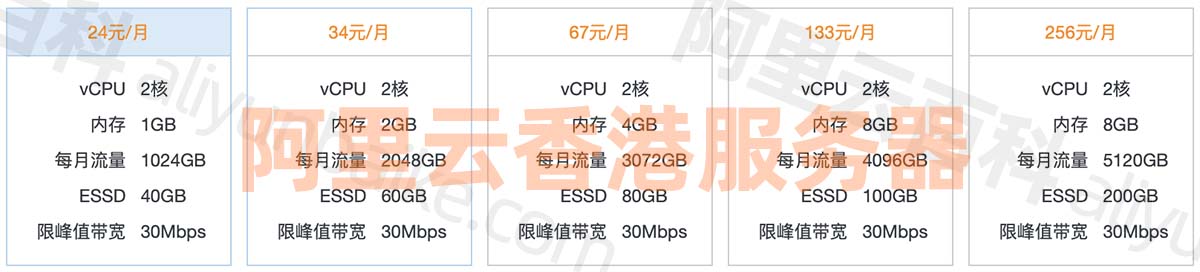
阿里云香港云服务器租用_BGP多线网络_CN2高速线路测试
阿里云香港服务器中国香港数据中心网络线路类型BGP多线精品,中国电信CN2高速网络高质量、大规格BGP带宽,运营商精品公网直连中国内地,时延更低,优化海外回中国内地流量的公网线路,可以提高国际业务访问质量。阿里云服务…...

C# 异步方法的使用场景
我一直认为C#的异步方法只是一堆华而不实的东西,坑特别多,比起直接自建线程也没有任何优势。 直到有一天,一个需求场景,让我再次想到了C#的异步方法。 需求场景如下:需要写一个程序控制机械臂完成各种动作。每个动作要…...

Lua 教程
Lua 教程 (今天又又又开新坑啦) Lua 教程 手册简介 Lua 是一种轻量小巧的脚本语言,用标准C语言编写并以源代码形式开放。 手册说明 Lua是什么? Lua 是一个小巧的脚本语言。是巴西里约热内卢天主教大学(Pontifical Catholic University of Rio de …...

CleanMyMac X2024版本有哪些常见的使用场景?
CleanMyMac X作为一款Mac电脑清理和优化工具,具有多种使用场景。以下是一些常见的使用场景: 清理系统垃圾文件:CleanMyMac X可以智能扫描Mac磁盘空间,清理系统冗余文件和各种软件应用产生的垃圾文件,如缓存、日志文件…...

《Docker快速入门:从0到1构建你的第一个容器!》
《Docker快速入门:从0到1构建你的第一个容器!》 前言 欢迎来到Docker的世界,一个让应用程序打包、部署和运行更加容易的神奇平台。Docker改变了我们对于应用开发和分发的看法,它通过容器技术让软件的携带和运行变得前所未有的轻…...

NLP_Transformer架构
文章目录 Transformer架构剖析编码器-解码器架构各种注意力的应用Transformer中的自注意力Transformer中的多头自注意力Transformer中的编码器-解码器注意力Transformer中的注意力掩码和因果注意力 编码器的输入和位置编码编码器的内部结构编码器的输出和编码器-解码器的连接解…...

CVE-2012-2311 漏洞复现
CVE-2012-2311 这个漏洞被爆出来以后,PHP官方对其进行了修补,发布了新版本5.4.2及5.3.12,但这个修复是不完全的,可以被绕过,进而衍生出CVE-2012-2311漏洞。 PHP的修复方法是对-进行了检查: if(query_str…...

多线程面试题汇总
多线程面试题汇总 一、多线程1、线程的生命周期2、线程的创建(函数创建)3、线程的创建(使用类)4、守护线程 二、全局解释器锁1、使用单线程实现累加到5000000002、使用多线程实现累加到5000000003、总结 三、线程安全1、多线程之数…...
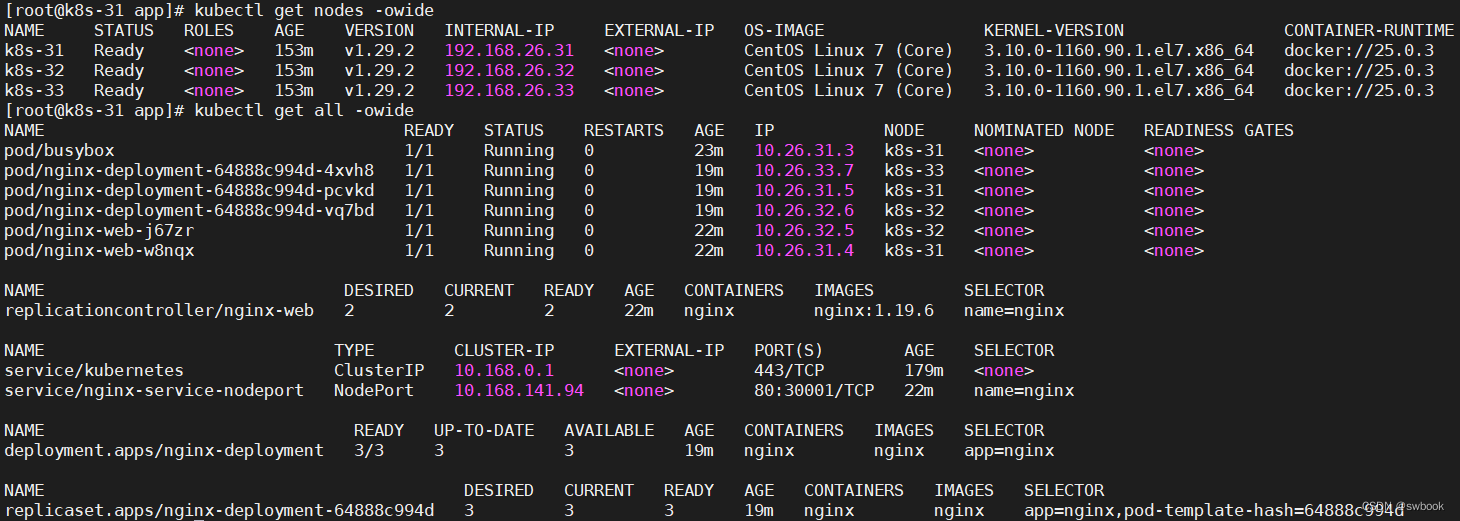
CentOS7.9+Kubernetes1.29.2+Docker25.0.3高可用集群二进制部署
CentOS7.9Kubernetes1.29.2Docker25.0.3高可用集群二进制部署 Kubernetes高可用集群(Kubernetes1.29.2Docker25.0.3)二进制部署二进制软件部署flannel v0.22.3网络,使用的etcd是版本3,与之前使用版本2不同。查看官方文档进行了解…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...