【数据结构】16 二叉树的定义,性质,存储结构(以及先序、后序、中序遍历)
二叉树
一个二叉树是一个有穷的结点集合。
它是由根节点和称为其左子树和右子树的两个不相交的二叉树组成的。
二叉树可具有以下5种形态。
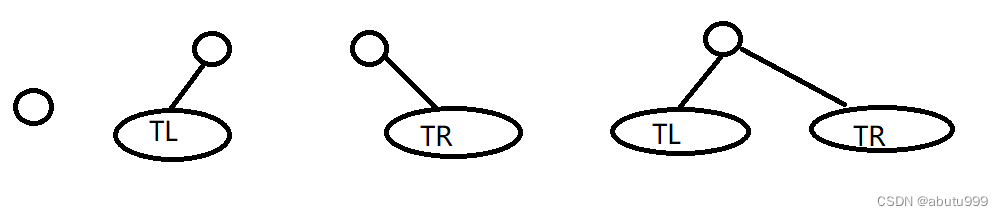
性质
- 一个二叉树第i层的最大结点数为 2 i − 1 2^{i-1} 2i−1, i ≥ 1 i \geq 1 i≥1
每层最大结点可以对应完美二叉树(满二叉树),其所有分支结点都存在左右子树,并且所有叶结点都在同一层上。
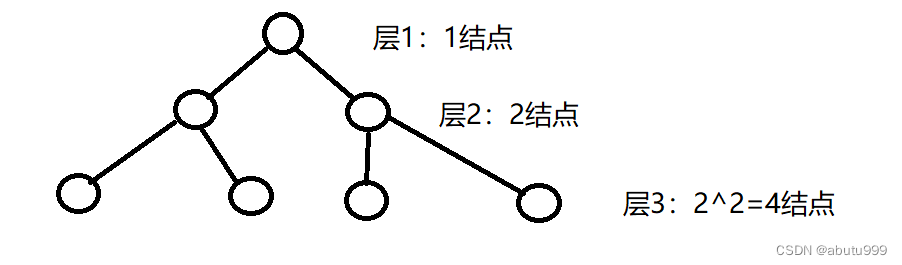
- 深度为k的二叉树有最大结点总数: 2 k − 1 2^k-1 2k−1, k ≥ 1 k \geq 1 k≥1
1 + 2 + . . . + 2 k − 1 = 2 k − 1 1 + 2 + ... +2^{k-1} = 2^k-1 1+2+...+2k−1=2k−1 - 对任何非空的二叉树 T n T_n Tn,若 n 0 n_0 n0是叶结点的个数, n 2 n_2 n2是度为2的非叶结点的个数,则: n 0 = n 2 + 1 n_0 = n_2 +1 n0=n2+1。
一颗二叉树:总结点数 = 叶节点 + 度为1的结点 + 度为2的结点
又:总结点数 = 总边数+1
且:总边数 = 2 ∗ 2* 2∗度为2的结点 + 度为1的结点
由此得到: n 0 = n 2 + 1 n_0 = n_2 +1 n0=n2+1 - 具有n个结点的完全二叉树的深度k为 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2{n} \rfloor +1 ⌊log2n⌋+1
(1) 满二叉树时:
k深度: 结点 2 k − 1 2^k-1 2k−1
n = 2 k − 1 n = 2^k-1 n=2k−1 得 k = l o g 2 n + 1 k = log_2{n+1} k=log2n+1
(2)最底层只有一个结点
k深度: 结点 2 k − 1 2^{k-1} 2k−1
解得: k = l o g 2 n + 1 k = log_2{n} +1 k=log2n+1
即 l o g 2 ( n + 1 ) ≤ k ≤ l o g 2 n + 1 log_2{(n+1)} \leq k \leq log_2n +1 log2(n+1)≤k≤log2n+1
则具有n个结点的完全二叉树的深度k为 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2{n} \rfloor +1 ⌊log2n⌋+1
存储结构
顺序存储
这种结构是川一组连续的存储单元(比如数组)存储二叉树结点的数据,结点的父子系是通过它们相对位置来反映的,而不需要任何附加的存储单元来存放指针,通常情况下顺序存储结构用于完全二叉树
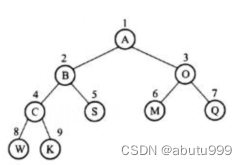
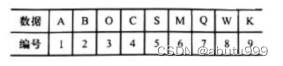
具体实现是从树的根结点开始,从上层至下层,每层从左到右,依次给结点编号并将数据存放到一个数组的对应单元中。
结点C的父结点是结点B,它的左孩子是结点w,右孩子是结点K。C结点存储单元的下标是4,将其除以2得到它的父结点B的存储单元下标,而将其乘以2则是它的左孩子w存储单元的下标,当然将其乘2再加1则是它右孩子K的存储单元下标。
链式存储
虽然顺序存储的空间利用率高,计算简单,但是其不适于一般的二叉树
如图为给定的二叉树。给出了从上至下、从左至右的层序存储的对应结点编号,其中灰色结点是为了满足顺序存储要求而增加的“虚”结点,可以在相应的存储单元存放一个特殊的数值,以区别于其他“实结点”。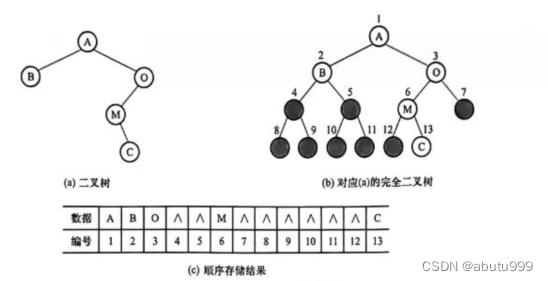
可以看到,5个结点的二叉树,顺序存储需要13个存储单元,超过一半的存储空间浪费掉了。更有甚者,对一个深度为h的右斜二叉树来讲,需要2-1个存储单元,而实际上该斜二叉树只有k个结点。
另外,二叉树的顺序存储方式避免不了顺序存储的固有缺点,即不易实现增加、删除操作。因此,二叉树的顺序存储方式适用于一定的条件,对于不需要修改的完全二叉树,是一种较好的选择。
实际上,二叉树的最常用表示方法是用链表表示,每个结点由数据和左右指针三个数据成员组成。
结构定义
typedef int ElementType;
typedef struct TNode* Position;
typedef Position BinTree;
struct TNode {ElementType Data;//结点数据BinTree Left; //指向左子树BinTree Right; //指向右子树
};操作实现
遍历
我们用L,V,R分别表示遍历左分支L,访问结点V,遍历右分支R,那么可以有以下6种情况:LVR,LRV,VLR,VRL,RLV,RVL。
规定:访问左分支在右分支之前,只剩下:LVR, LRV, VLR。
我们按照V的位置分别将其命名为:中序遍历,后序遍历,先序遍历
中序遍历
对树的任一结点的访问是在先遍历完其左子树后进行的,访问此结点后,在对其右子树遍历
遇到每个结点,其遍历过程
- 中序遍历左子树
- 访问根节点
- 中序遍历右节点
void InorderTraveral(BinTree BT) {if (BT) {InorderTraveral(BT->Left);printf("%d\n, BT->Data");InorderTraveral(BT->Right);}
}
后序遍历
对结点的左右子树先进行遍历,然后才对此结点访问。遍历是从根节点开始,遇到每个结点时,其遍历过程是:
- 后序遍历其左子树
- 后序遍历其右子树
- 访问根节点
void PostorderTraversal(BinTree BT) {if (BT) {PostorderTraversal(BT->Left);printf("%d\n, BT->Data");PostorderTraversal(BT->Right);}
}
先序遍历
对结点的访问是在其左、右子树遍历之前进行的。遍历是从根节点开始,遇到每个结点时,其遍历过程是:
- 访问根结点
- 先序遍历其左子树
- 先序遍历其右子树
void PreorderTraversal(BinTree BT) {if (BT) {printf("%d\n, BT->Data");PreorderTraversal(BT->Left);PreorderTraversal(BT->Right);}
}非递归遍历
在沿左子树深入时,进入一个结点就将其压入堆栈。
若是先序遍历,则在入栈之前访问之;当沿左分支深入不下去时,则返回,即从堆栈中弹出前面压入的结点;
若为中序遍历,则此时访同该结点,然后从该结点的右子树继续深入;
若为后序遍历,则将此结点二次入栈,然后从该结点的右子树继续深入,与前面类同,仍为进入一个结点入栈一个结点,深入不下去再返回,直到第二次从栈里弹出该结点,才访问之。
对于非递归中序遍历,遇到一个节点就将其压栈,并去遍历其左子树;当左子树结束后,从栈顶弹出结点并访问它,然后按其右指针再去中序遍历该节点的右子树。
void InorderTraversalUn(BinTree BT) {BinTree T;Stack S = CreateStack(100);T = BT;while (T || !IsEmpty(S)) {while (T) {Push(S, T);T = T->Left;}T = Pop(S);printf("%d\n, T->Data");T = T->Right;}}
层序遍历
层序遍历是按照树的层次,从第一层的根结点开始向下逐层访问每个结点,对每一层的结点按照从左到右的顺序访问。
可以设置一个队列结构,遍历从根节点开始,首先将根节指针入队,然后执行以下操作:
- 从队列取出一个元素
- 访问该元素所指向的结点
- 若元素所指向的结点的左右孩子非空,将其左、右孩子的指针入队。
不断执行这三步,直到队列为空。
void LevelorderTraversal(BinTree BT) {Queue Q;BinTree T;T = BT;Q = CreateQueue(100);AddQ(Q, T);while (!IsEmptyQ(Q)) {T = DeleteQ(Q);printf("%d\n, T->Data");if (!T->Left) { AddQ(Q, T->Left); }if (!T->Right) { AddQ(Q, T->Right); }}
}
相关文章:

【数据结构】16 二叉树的定义,性质,存储结构(以及先序、后序、中序遍历)
二叉树 一个二叉树是一个有穷的结点集合。 它是由根节点和称为其左子树和右子树的两个不相交的二叉树组成的。 二叉树可具有以下5种形态。 性质 一个二叉树第i层的最大结点数为 2 i − 1 2^{i-1} 2i−1, i ≥ 1 i \geq 1 i≥1 每层最大结点可以对应完美二叉树(…...
GPT SOVITS项目 一分钟克隆 (文字输出)
步骤流程:(首先使用UVR 提取人声文件,然后按下面步骤进行) 注意这里提交的音频是参考的音频...

python34-Python列表和元组之加法
列表和元组支持加法运算,加法的和就是两个列表或元组所包含的元素的总和。 需要指出的是,列表只能和列表相加;元组只能和元组相加;元组不能直接和列表相加。 如下代码示范了元组和列表的加法运算。 # !/usr/bin/env python# -*- coding: utf-8 -*-# T…...
)
不做程序员了(转岗半年后对程序员岗位的思考)
不做程序员了(转岗半年后对程序员岗位的思考) 前言 好久没有更新了,已经久到CSDN的小编来问我为什么不更了。原因是我半年前转岗了,不再做程序员了,由程序员变为了产品经理。废话不多说,换个视角来给大家…...
DS:八大排序之直接插入排序、希尔排序和选择排序
创作不易,感谢三连支持!! 一、排序的概念及运用 1.1 排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起 来的操作。稳定性&…...
)
【MySQL】-21 MySQL综合-8(MySQL默认值+MySQL非空约束+MySQL查看表中的约束)
MySQL默认值MySQL非空约束MySQL查看表中的约束 MySQL默认值在创建表时设置默认值约束在修改表MySQL默认值在创建表时设置默认值约束在修改表时添加默认值约束删除默认值约束删除默认值约束 MySQL非空约束在创建表时设置非空约束在修改表时添加非空约束删除非空约束 MySQL查看表…...

力扣hot3--并查集+哈希
第一想法是排个序然后遍历一遍,but时间复杂度就超啦 并查集居然与哈希结合了() 已经好久没用过并查集了,,,我们用哈希表f_node中来记录原结点的父节点,其中key是原结点,value是父节点…...
微信网页版能够使用(会顶掉微信app的登陆)
一、文件结构 新建目录chrome新建icons,其中图片你自己找吧新建文件manifest.json新建文件wx-rules.json 二、文件内容 对应的png你们自己改下 1、manifest.json {"manifest_version": 3,"name": "wechat-need-web","author…...
会影响word文档中插入图片的分辨率吗?)
word软件中硬件图像加速有什么用处?禁用硬件图形加速(G)会影响word文档中插入图片的分辨率吗?
问题描述:word软件中硬件图像加速有什么用处?禁用硬件图形加速(G)会影响word文档中插入图片的分辨率吗? 问题解答: 在 Microsoft Word 中,硬件图形加速主要用于提高图形元素的渲染速度和性能,特别是处理大…...
.NET Core MongoDB数据仓储和工作单元模式封装
前言 上一章我们把系统所需要的MongoDB集合设计好了,这一章我们的主要任务是使用.NET Core应用程序连接MongoDB并且封装MongoDB数据仓储和工作单元模式,因为本章内容涵盖的有点多关于仓储和工作单元的使用就放到下一章节中讲解了。仓储模式(R…...

lua:有关表访问的metamethod
针对在两种正常状态:表的不存在的域的查询和修改,Lua也提供了改变 tables的行为的方法。 index metamethod 我们可以通过index元方法来实现访问table内部不存在的域时人为操控返回数据。 比如以下测试代码: local set {1,2,3} setmetata…...
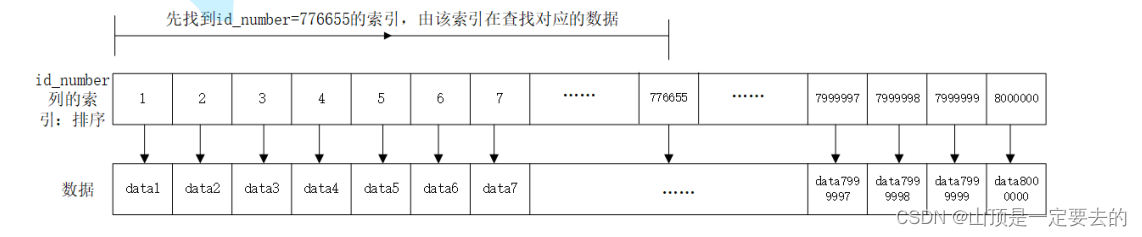
【MySQL】索引事务
MySQL索引事务 1. 索引1.1 概念1.2 作用1.3 使用场景1.4 使用1.5 案例 2. 事务2.2 事物的概念2.3 使用 3. 内容重点总结 1. 索引 1.1 概念 索引是一种特殊的文件,包含着对数据表里所有记录的引用指针。可以对表中的一列或多列创建索引, 并指定索引的类…...

ChatGPT重大升级:能自动记住用户的习惯和喜好,用户有权决定是否共享数据给OpenAI
OpenAI刚刚宣布了ChatGPT的一项激动人心的更新! OpenAI在ChatGPT中新加了记忆功能和用户控制选项,这意味着GPT能够在与用户的互动中记住之前的对话内容,并利用这些信息在后续的交谈中提供更加相关和定制化的回答。 这一功能目前正处于测试阶…...

CSS设置盒子阴影
语法 box-shadow: *h-shadow v-shadow blur spread color* inset; 注释: box-shadow向框添加一个或多个阴影. 该属性是由逗号分隔的阴影列表,每个阴影由2-4个长度值、可选的颜色值及可选的inset关键词来规定。省略长度的值是0。 外阴影 a、给元素右边框和下边框加外阴影——把…...
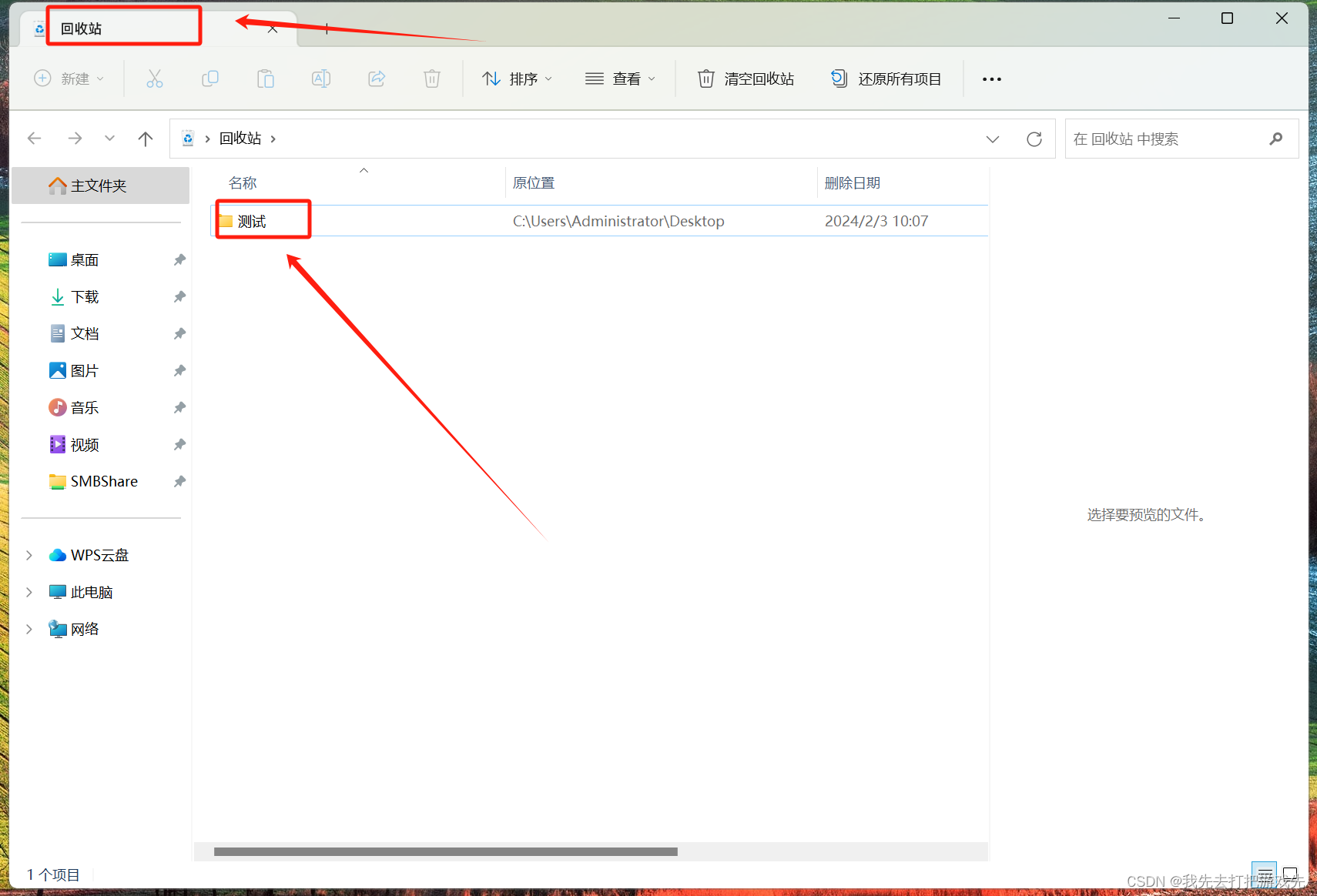
文件夹删不掉,显示在另一个文件中打开怎么办
问题: 一、想要删掉这个文件夹,却因为文件夹中的文件打开了删不掉,这里我因为做的测试,所以是知道打开了什么 二、一般情况下文件比较多时,是不知道打开了什么的,长这个样子 解决: 一、打开任…...
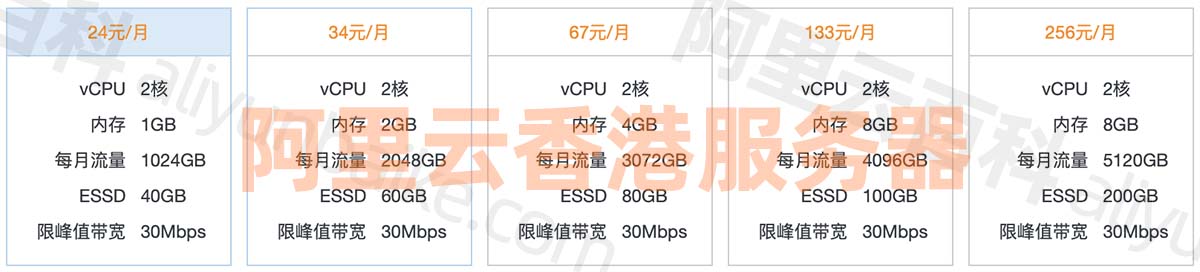
阿里云香港云服务器租用_BGP多线网络_CN2高速线路测试
阿里云香港服务器中国香港数据中心网络线路类型BGP多线精品,中国电信CN2高速网络高质量、大规格BGP带宽,运营商精品公网直连中国内地,时延更低,优化海外回中国内地流量的公网线路,可以提高国际业务访问质量。阿里云服务…...

C# 异步方法的使用场景
我一直认为C#的异步方法只是一堆华而不实的东西,坑特别多,比起直接自建线程也没有任何优势。 直到有一天,一个需求场景,让我再次想到了C#的异步方法。 需求场景如下:需要写一个程序控制机械臂完成各种动作。每个动作要…...

Lua 教程
Lua 教程 (今天又又又开新坑啦) Lua 教程 手册简介 Lua 是一种轻量小巧的脚本语言,用标准C语言编写并以源代码形式开放。 手册说明 Lua是什么? Lua 是一个小巧的脚本语言。是巴西里约热内卢天主教大学(Pontifical Catholic University of Rio de …...

CleanMyMac X2024版本有哪些常见的使用场景?
CleanMyMac X作为一款Mac电脑清理和优化工具,具有多种使用场景。以下是一些常见的使用场景: 清理系统垃圾文件:CleanMyMac X可以智能扫描Mac磁盘空间,清理系统冗余文件和各种软件应用产生的垃圾文件,如缓存、日志文件…...

《Docker快速入门:从0到1构建你的第一个容器!》
《Docker快速入门:从0到1构建你的第一个容器!》 前言 欢迎来到Docker的世界,一个让应用程序打包、部署和运行更加容易的神奇平台。Docker改变了我们对于应用开发和分发的看法,它通过容器技术让软件的携带和运行变得前所未有的轻…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
