无人驾驶LQR控制算法 c++ 实现
参考博客:
(1)LQR的理解与运用 第一期——理解篇
(2)线性二次型调节器(LQR)原理详解
(3)LQR控制基本原理(包括Riccati方程具体推导过程)
(4)【基础】自动驾驶控制算法第五讲 连续方程的离散化与离散LQR原理
0 前言
LQR:线性二次调节器,设计状态反馈控制器的方法
1 LQR算法原理
系统: x ˙ = A x + B u \dot x=Ax+Bu x˙=Ax+Bu
线性反馈控制器: u = − K x u=-Kx u=−Kx

让系统稳定的条件是矩阵 A c l A_{cl} Acl的特征值实部均为负数。因此我们可以手动选择几个满足上述条件的特征值,然后反解出K,从而得到控制器。
代价函数 J J J

在系统稳定的前提下,通过设计合适的K,让代价函数J最小。
Q大:希望状态变量x更快收敛
R大:希望输入量u收敛更快,以更小的代价实现系统稳定
1.1 连续时间LQR推导
具体推导参见博客:线性二次型调节器(LQR)原理详解
求解连续时间LQR反馈控制器参数K的过程:
(1)设计参数矩阵Q、R
(2)求解Riccati方程 A T P + P A − P B R − 1 B T P + Q = 0 A^TP+PA-PBR^{-1}B^TP+Q=0 ATP+PA−PBR−1BTP+Q=0得到P
(3)计算 K = R − 1 B T P K=R^{-1}B^TP K=R−1BTP得到反馈控制量 u = − k x u=-kx u=−kx
1.2 离散时间LQR推导
离散情况下的LQR推导有最小二乘法和动态规划算法
详细推导见博客:连续时间LQR和离散时间LQR笔记
离散系统:
x ( K + 1 ) = A x ( k ) + B u ( k ) x(K+1)=Ax(k)+Bu(k) x(K+1)=Ax(k)+Bu(k)
代价函数:
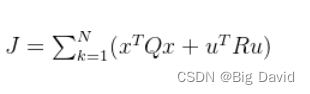
设计步骤:
① 确定迭代范围N
② 设置迭代初始值 P N = Q P_N=Q PN=Q
③ t = N , . . . , 1 t=N,...,1 t=N,...,1,从后向前循环迭代求解离散时间的代数Riccati方程
P t − 1 = Q + A T P t A − A T P t B ( R + B T P t + 1 B ) − 1 B T P t A P_{t-1}=Q+A^TP_tA-A^TP_tB(R+B^TP_{t+1}B)^{-1}B^TP_tA Pt−1=Q+ATPtA−ATPtB(R+BTPt+1B)−1BTPtA
④ t = 0 , . . . , N t=0,...,N t=0,...,N循环计算反馈系数 K t = ( R + B T P t + 1 B ) − 1 B T P t + 1 A K_t=(R+B^TP_{t+1}B)^{-1}B^TP_{t+1}A Kt=(R+BTPt+1B)−1BTPt+1A 得到控制量 u t = − K t x t u_t=-K_tx_t ut=−Ktxt
2 LQR代码
主要步骤:
(1)确定迭代范围N,预设精度EPS
(2)设置迭代初始值P = Qf,Qf = Q
(3)循环迭代, t = 1 , . . . , N t=1,...,N t=1,...,N
P n e w = Q + A T P A − A T P B ( R + B T P B ) − 1 B T P A P _{new} =Q+A ^TPA−A ^TPB(R+B ^T PB) ^{−1}B ^TPA Pnew=Q+ATPA−ATPB(R+BTPB)−1BTPA
若 ∣ ∣ P n e w − P ∣ ∣ < E P S ||P_{new}-P||<EPS ∣∣Pnew−P∣∣<EPS:跳出循环;否则: P = P n e w P=P_{new} P=Pnew
(4)计算反馈系数 K = ( R + B T P n e w B ) − 1 B T P n e w A K=(R + B^TP_{new}B)^{-1}B^TP_{new}A K=(R+BTPnewB)−1BTPnewA
(5)最终的优化控制量 u ∗ = − K x u^*=-Kx u∗=−Kx
Reference_path.h
#pragma once#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <Eigen/Dense>using namespace std;
using namespace Eigen;#define PI 3.1415926struct refTraj
{MatrixXd xref, dref;int ind;
};struct parameters
{int L;int NX, NU, T;double dt;
};class ReferencePath
{
public:ReferencePath();vector<double> calcTrackError(vector<double> robot_state);double normalizeAngle(double angle);// 计算参考轨迹点,统一化变量数组,便于后面MPC优化使用.refTraj calc_ref_trajectory(vector<double> robot_state, parameters param, double dl = 1.0);public:vector<vector<double>> ref_path; // x, y, 切线方向, kvector<double> ref_x, ref_y;
};
Reference_path.cpp
#include "Reference_path.h"ReferencePath::ReferencePath()
{ref_path = vector<vector<double>>(1000, vector<double>(4));// 生成参考轨迹for (int i = 0; i < 1000; i++){ref_path[i][0] = 0.1 * i;ref_path[i][1] = 2 * sin(ref_path[i][0] / 3.0);ref_x.push_back(ref_path[i][0]);ref_y.push_back(ref_path[i][1]);}double dx, dy, ddx, ddy;for (int i = 0; i < ref_path.size(); i++){if (i == 0) {dx = ref_path[i + 1][0] - ref_path[i][0];dy = ref_path[i + 1][1] - ref_path[i][1];ddx = ref_path[2][0] + ref_path[0][0] - 2 * ref_path[1][0];ddy = ref_path[2][1] + ref_path[0][1] - 2 * ref_path[1][1];} else if (i == ref_path.size() - 1) {dx = ref_path[i][0] - ref_path[i- 1][0];dy = ref_path[i][1] - ref_path[i- 1][1];ddx = ref_path[i][0] + ref_path[i- 2][0] - 2 * ref_path[i - 1][0];ddy = ref_path[i][1] + ref_path[i - 2][1] - 2 * ref_path[i - 1][1];} else {dx = ref_path[i + 1][0] - ref_path[i][0];dy = ref_path[i + 1][1] - ref_path[i][1];ddx = ref_path[i + 1][0] + ref_path[i - 1][0] - 2 * ref_path[i][0];ddy = ref_path[i + 1][1] + ref_path[i - 1][1] - 2 * ref_path[i][1];}ref_path[i][2] = atan2(dy, dx);//计算曲率:设曲线r(t) =(x(t),y(t)),则曲率k=(x'y" - x"y')/((x')^2 + (y')^2)^(3/2).ref_path[i][3] = (ddy * dx - ddx * dy) / pow((dx * dx + dy * dy), 3.0 / 2); // k计算}
}
// 计算跟踪误差
vector<double> ReferencePath::calcTrackError(vector<double> robot_state)
{double x = robot_state[0], y = robot_state[1];vector<double> d_x(ref_path.size()), d_y(ref_path.size()), d(ref_path.size());for (int i = 0; i < ref_path.size(); i++){d_x[i]=ref_path[i][0]-x;d_y[i]=ref_path[i][1]-y;d[i] = sqrt(d_x[i]*d_x[i]+d_y[i]*d_y[i]);}double min_index = min_element(d.begin(), d.end()) - d.begin();double yaw = ref_path[min_index][2];double k = ref_path[min_index][3];double angle = normalizeAngle(yaw - atan2(d_y[min_index], d_x[min_index]));double error = d[min_index];if (angle < 0) error *= -1;return {error, k, yaw, min_index};
}double ReferencePath::normalizeAngle(double angle)
{while (angle > PI){angle -= 2 * PI;}while (angle < -PI){angle += 2 * PI;}return angle;
}// 计算参考轨迹点,统一化变量数组,只针对MPC优化使用
// robot_state 车辆的状态(x,y,yaw,v)
refTraj ReferencePath::calc_ref_trajectory(vector<double> robot_state, parameters param, double dl)
{vector<double> track_error = calcTrackError(robot_state);double e = track_error[0], k = track_error[1], ref_yaw = track_error[2], ind = track_error[3];refTraj ref_traj;ref_traj.xref = MatrixXd(param.NX, param.T + 1);ref_traj.dref = MatrixXd (param.NU,param.T);int ncourse = ref_path.size();ref_traj.xref(0,0)=ref_path[ind][0];ref_traj.xref(1,0)=ref_path[ind][1];ref_traj.xref(2,0)=ref_path[ind][2];//参考控制量[v,delta]double ref_delta = atan2(k * param.L, 1);for(int i=0;i<param.T;i++){ref_traj.dref(0,i)=robot_state[3];ref_traj.dref(1,i)=ref_delta;}double travel = 0.0;for(int i = 0; i < param.T + 1; i++){travel += abs(robot_state[3]) * param.dt;double dind = (int)round(travel / dl);if(ind + dind < ncourse){ref_traj.xref(0,i)=ref_path[ind + dind][0];ref_traj.xref(1,i)=ref_path[ind + dind][1];ref_traj.xref(2,i)=ref_path[ind + dind][2];}else{ref_traj.xref(0,i)=ref_path[ncourse-1][0];ref_traj.xref(1,i)=ref_path[ncourse-1][1];ref_traj.xref(2,i)=ref_path[ncourse-1][2];}}return ref_traj;
}
LQR.h
#pragma once#define EPS 1.0e-4
#include <Eigen/Dense>
#include <vector>
#include <iostream>
using namespace std;
using namespace Eigen;class LQR {
private:int N;
public:LQR(int n);MatrixXd calRicatti(MatrixXd A, MatrixXd B, MatrixXd Q, MatrixXd R);double LQRControl(vector<double> robot_state, vector<vector<double>> ref_path, double s0, MatrixXd A, MatrixXd B, MatrixXd Q, MatrixXd R);
};
LQR.cpp
#include "LQR.h"LQR::LQR(int n) : N(n) {}
// 解代数里卡提方程
MatrixXd LQR::calRicatti(MatrixXd A, MatrixXd B, MatrixXd Q, MatrixXd R)
{MatrixXd Qf = Q;MatrixXd P_old = Qf;MatrixXd P_new;// P _{new} =Q+A ^TPA−A ^TPB(R+B ^T PB) ^{−1}B ^TPAfor (int i = 0; i < N; i++){P_new = Q + A.transpose() * P_old * A - A.transpose() * P_old * B * (R + B.transpose() * P_old * B).inverse() * B.transpose() * P_old * A;if ((P_new - P_old).maxCoeff() < EPS && (P_old - P_new).maxCoeff() < EPS) break;P_old = P_new;}return P_new;
}double LQR::LQRControl(vector<double> robot_state, vector<vector<double>> ref_path, double s0, MatrixXd A, MatrixXd B, MatrixXd Q, MatrixXd R)
{MatrixXd X(3, 1);X << robot_state[0] - ref_path[s0][0],robot_state[1] - ref_path[s0][1],robot_state[2] - ref_path[s0][2];MatrixXd P = calRicatti(A, B, Q, R);// K=(R + B^TP_{new}B)^{-1}B^TP_{new}AMatrixXd K = (R + B.transpose() * P * B).inverse() * B.transpose() * P * A;MatrixXd u = -K * X; // [v - ref_v, delta - ref_delta]return u(1, 0);
}
main.cpp
#include "LQR.h"
#include "KinematicModel.h"
#include "matplotlibcpp.h"
#include "Reference_path.h"
#include "pid_controller.h"namespace plt = matplotlibcpp;int main()
{int N = 500; // 迭代范围double Target_speed = 7.2 / 3.6;MatrixXd Q(3,3);Q << 3,0,0,0,3,0,0,0,3;MatrixXd R(2,2);R << 2.0,0.0,0.0,2.0;//保存机器人(小车)运动过程中的轨迹vector<double> x_, y_;ReferencePath referencePath;KinematicModel model(0, 1.0, 0, 0, 2.2, 0.1);PID_controller PID(3, 0.001, 30, Target_speed, 15.0 / 3.6, 0.0);LQR lqr(N);vector<double> robot_state;for (int i = 0; i < 700; i++){plt::clf();robot_state = model.getState();vector<double> one_trial = referencePath.calcTrackError(robot_state);double k = one_trial[1], ref_yaw = one_trial[2], s0 = one_trial[3];double ref_delta = atan2(k * model.L, 1); // L = 2.2vector<MatrixXd> state_space = model.stateSpace(ref_delta, ref_yaw);double delta = lqr.LQRControl(robot_state, referencePath.ref_path, s0, state_space[0], state_space[1], Q, R);delta = delta + ref_delta;double a = PID.calOutput(model.v);model.updateState(a, delta);cout << "Speed: " << model.v << " m/s" << endl;x_.push_back(model.x);y_.push_back(model.y);//画参考轨迹plt::plot(referencePath.ref_x, referencePath.ref_y, "b--");plt::grid(true);plt::ylim(-5, 5);plt::plot(x_, y_, "r");plt::pause(0.01);}const char* filename = "./LQR.png";plt::save(filename);plt::show();return 0;
}
CMakeList.txt
cmake_minimum_required(VERSION 3.0.2)
project(LQR)## Compile as C++11, supported in ROS Kinetic and newer
# add_compile_options(-std=c++11)## Find catkin macros and libraries
## if COMPONENTS list like find_package(catkin REQUIRED COMPONENTS xyz)
## is used, also find other catkin packages
find_package(catkin REQUIRED COMPONENTSroscppstd_msgs
)set(CMAKE_CXX_STANDARD 11)file(GLOB_RECURSE PYTHON2.7_LIB "/usr/lib/python2.7/config-x86_64-linux-gnu/*.so")
set(PYTHON2.7_INLCUDE_DIRS "/usr/include/python2.7")catkin_package(
# INCLUDE_DIRS include
# LIBRARIES huatu
# CATKIN_DEPENDS roscpp std_msgs
# DEPENDS system_lib
)include_directories(include${PYTHON2.7_INLCUDE_DIRS}
)add_executable(lqr_controller src/LQR.cppsrc/KinematicModel.cppsrc/main.cppsrc/pid_controller.cppsrc/Reference_path.cpp)
target_link_libraries(lqr_controller ${PYTHON2.7_LIB})
3 PID vs Pure pursuit vs Stanley vs LQR
横向控制算法
(1)PID:鲁棒性较差,对路径无要求,转弯不会内切,速度增加会有一定超调,速度增加稳态误差变大,适用场景:路径曲率较小及低速的跟踪场景
(2)Pure pursuit:鲁棒性较好,对路径无要求,转弯内切速度增加变得严重,速度增加会有一定超调,速度增加稳态误差变大,适用场景:路径连续或不连续或者低速的跟踪场景
(3)Stanley:鲁棒性好,对路径要求曲率连续,转弯不会内切,速度增加会有一定超调,速度增加稳态误差变大,适用场景:路径平滑的中低速跟踪场景
(4)LQR:鲁棒性较差,对路径要求曲率连续,不会转弯内切,曲率快速变化时超调严重,稳态误差小,除非速度特别大,适用场景:路径平滑的中高速城市驾驶跟踪场景
相关文章:
无人驾驶LQR控制算法 c++ 实现
参考博客: (1)LQR的理解与运用 第一期——理解篇 (2)线性二次型调节器(LQR)原理详解 (3)LQR控制基本原理(包括Riccati方程具体推导过程) (4)【基础…...
Karnaugh map (卡诺图)
【Leetcode】 289. Game of Life According to Wikipedia’s article: “The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.” The board is made up of an m x n grid of cells, wh…...

C# CAD 框选pdf输出
在C#中进行AutoCAD二次开发时,实现框选(窗口选择)实体并输出这些实体到PDF文件通常涉及以下步骤: public ObjectIdCollection GetSelectedEntities() {using (var acTrans HostApplicationServices.WorkingDatabase.Transaction…...

【Linux】 Linux 小项目—— 进度条
进度条 基础知识1 \r && \n2 行缓冲区3 函数介绍 进度条实现版本 1代码实现运行效果 版本2 Thanks♪(・ω・)ノ谢谢阅读!!!下一篇文章见!!! 基础知识 1 \r &&a…...
Sora和Pika,RunwayMl,Stable Video对比!网友:Sora真王者,其他都是弟
大家好,我是木易,一个持续关注AI领域的互联网技术产品经理,国内Top2本科,美国Top10 CS研究生,MBA。我坚信AI是普通人变强的“外挂”,所以创建了“AI信息Gap”这个公众号,专注于分享AI全维度知识…...

Go内存优化与垃圾收集
Go提供了自动化的内存管理机制,但在某些情况下需要更精细的微调从而避免发生OOM错误。本文介绍了如何通过微调GOGC和GOMEMLIMIT在性能和内存效率之间取得平衡,并尽量避免OOM的产生。原文: Memory Optimization and Garbage Collector Management in Go 本…...

【Spring】Bean 的生命周期
一、Bean 的生命周期 Spring 其实就是一个管理 Bean 对象的工厂,它负责对象的创建,对象的销毁等 所谓的生命周期就是:对象从创建开始到最终销毁的整个过程 什么时候创建 Bean 对象?创建 Bean 对象的前后会调用什么方法…...
云计算基础-存储基础
存储概念 什么是存储: 存储就是根据不同的应用程序环境,通过采取合理、安全、有效的方式将数据保存到某些介质上,并能保证有效的访问,存储的本质是记录信息的载体。 存储的特性: 数据临时或长期驻留的物理介质需要保…...
问题:人的安全知识和技能是天生的。() #媒体#知识分享#学习方法
问题:人的安全知识和技能是天生的。() 人的安全知识和技能是天生的。() 参考答案如图所示 问题:()是党和国家的根本所在、命脉所在,是全国各族人民的利益所在、幸福所在。 A.人民当家作主 B.坚持和完善…...
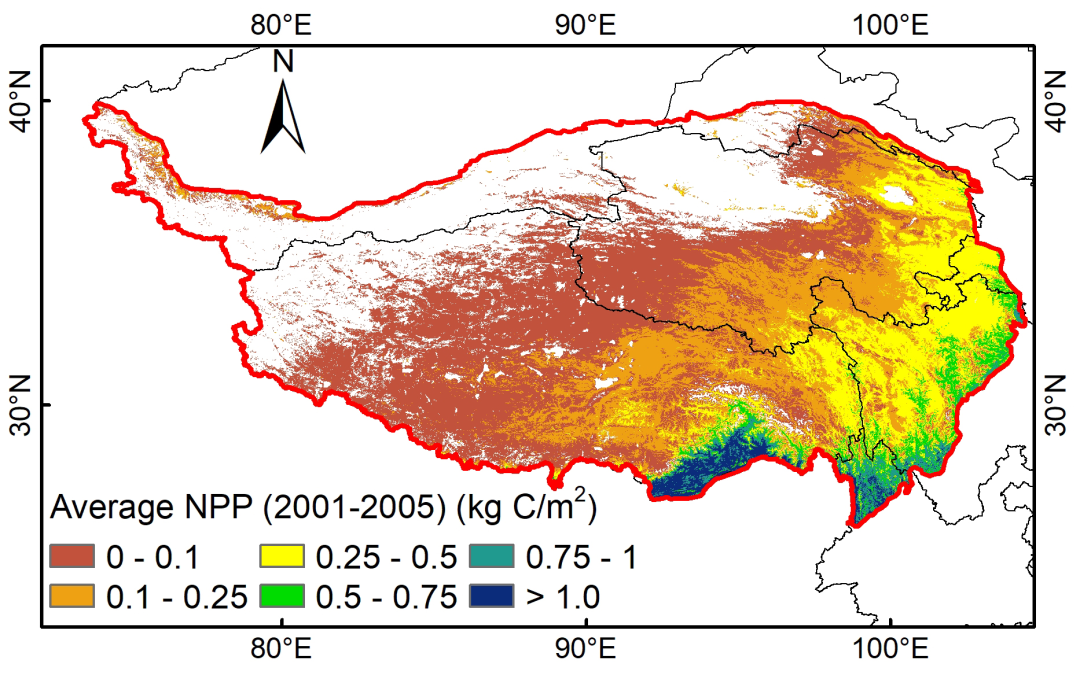
【数据分享】2001~2020年青藏高原植被净初级生产力数据集
各位同学们好,今天和大伙儿分享的是2001~2020年青藏高原植被净初级生产力数据集。如果大家有下载处理数据等方面的问题,您可以私信或评论。 朱军涛. (2022). 青藏高原植被净初级生产力数据集(2001-2020). 国家青藏高原数据中心. …...

【Spring MVC篇】返回响应
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【Spring MVC】 本专栏旨在分享学习Spring MVC的一点学习心得,欢迎大家在评论区交流讨论💌 目录 一、返回静态页面…...
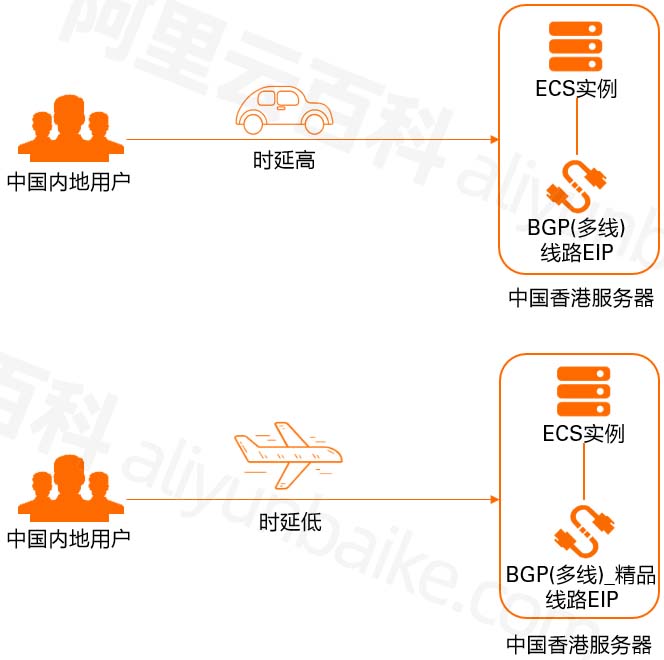
阿里云BGP多线精品EIP香港CN2线路低时延,价格贵
阿里云香港等地域服务器的网络线路类型可以选择BGP(多线)和 BGP(多线)精品,普通的BGP多线和精品有什么区别?BGP(多线)适用于香港本地、香港和海外之间的互联网访问。使用BGP…...
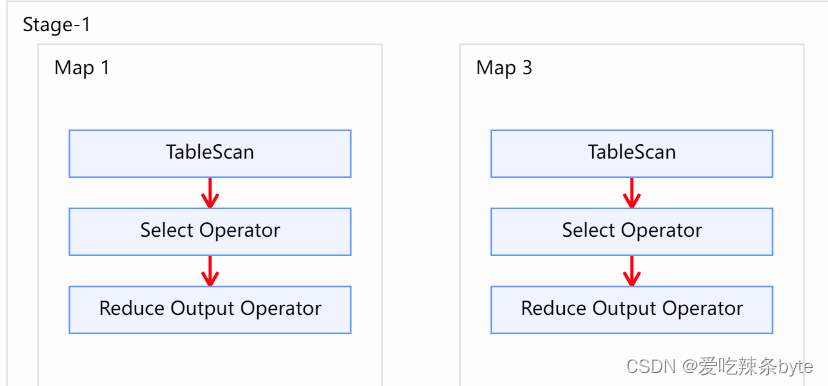
(08)Hive——Join连接、谓词下推
前言 Hive-3.1.2版本支持6种join语法。分别是:inner join(内连接)、left join(左连接)、right join(右连接)、full outer join(全外连接)、left semi join(左…...

创新技巧|迁移到 Google Analytics 4 时如何保存历史 Universal Analytics 数据
Google Universal Analytics 从 2023 年 7 月起停止收集数据(除了付费 GA360 之外)。它被Google Analytics 4取代。为此,不少用户疑惑:是否可以将累积(历史)数据从 Google Analytics Universal 传输到 Goog…...

一个小而实用的 Python 包 pangu,实现在中文和半宽字符(字母、数字和符号)之间自动插入空格
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一个小巧的库,可以避免自己重新开发功能。利用 Python 包 pangu,可以轻松实现在 CJK(中文、日文、韩文)和半宽字符(字母、数字和符号…...

openJudge | 中位数 C语言
总时间限制: 2000ms 内存限制: 65536kB 描述 中位数定义:一组数据按从小到大的顺序依次排列,处在中间位置的一个数或最中间两个数据的平均值(如果这组数的个数为奇数,则中位数为位于中间位置的那个数;如果这组数的个…...
ctfshow-文件上传(web151-web161)
目录 web151 web152 web153 web154 web155 web156 web157 web158 web159 web160 web161 web151 提示前台验证不可靠 那限制条件估计就是在前端设置的 上传php小马后 弹出了窗口说不支持的格式 查看源码 这一条很关键 这种不懂直接ai搜 意思就是限制了上传类型 允许…...

cudnn免登录下载
现在要下载cuDNN,点击下载的页面后都是出现要求先加入Nvidia developers才能进行下载,但这个注册的过程非常慢,常常卡在第二个步骤,这里根据亲身的经验介绍一个可以绕过这个注册或登陆步骤的方式直接下载cuDNN。遇到此类问题的可以…...
SQLyog安装配置(注册码)连接MySQL
下载资源 博主给你打包好了安装包,在网盘里,只有几Mb,防止你下载到钓鱼软件 快说谢谢博主(然后心甘情愿的点个赞~😊) SQLyog.zip 安装流程 ①下载好压缩包后并解压 ②打开文件夹,双击安装包 ③…...
java+SSM+mysql 开放式实验管理系统78512-计算机毕业设计项目选题推荐(免费领源码)
摘 要 我国高校开放式实验管理普遍存在实验设备使用率较低、管理制度不完善,实验设备共享程度不高等诸多问题。要在更大范围推行开放式实验管理,就必须在开放式实验教学管理流程中,通过引入信息化管理加大信息技术在其中的应用,才能真正发挥这种教学模式的开放性优势。 本系统…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...
