VueCLI核心知识3:全局事件总线、消息订阅与发布
这两种方式都可以实现任意两个组件之间的通信
1 全局事件总线
1.安装全局事件总线
import Vue from 'vue'
import App from './App.vue'Vue.config.productionTip = false/* 1.第一种写法 */
// const Demo = Vue.extend({})
// const d = new Demo()// Vue.prototype.x = d // 把Demo实例挂载到Vue的原型上,这样所有Vue实例都可以访问到xnew Vue({el: '#app',render: h => h(App),/* 2. 第二种写法 */beforeCreate() {Vue.prototype.$bus = this // 安装全局总线},
})2.使用事件总线
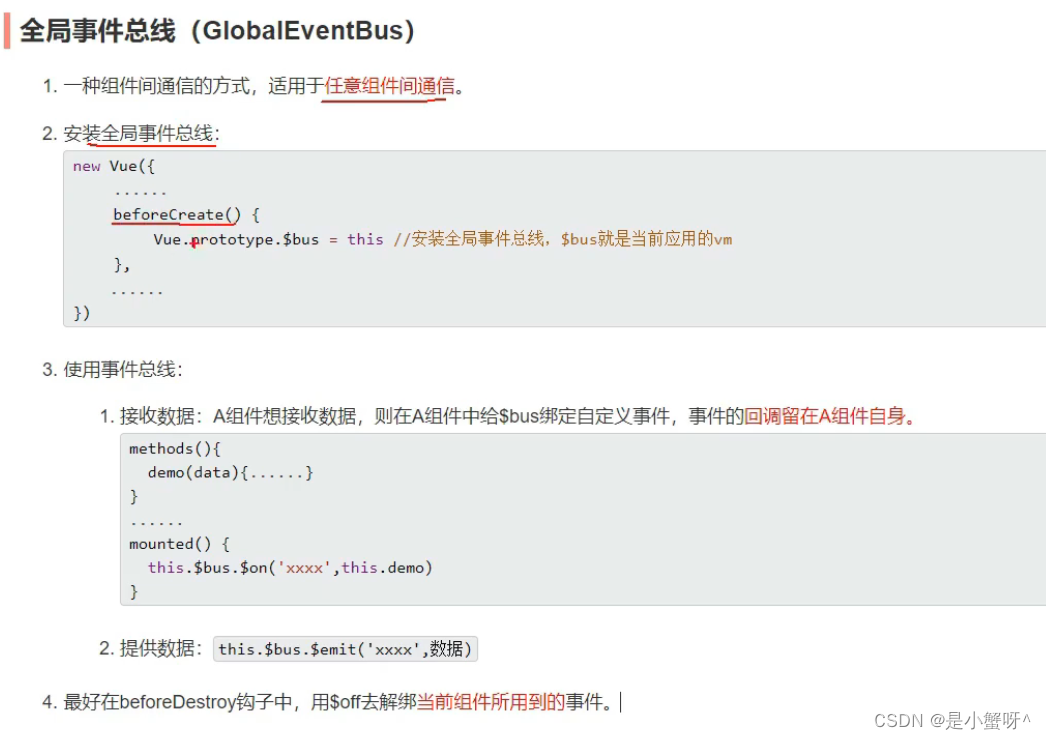
(1).发送数据

(2).接收数据

总结:
2 消息订阅与发布
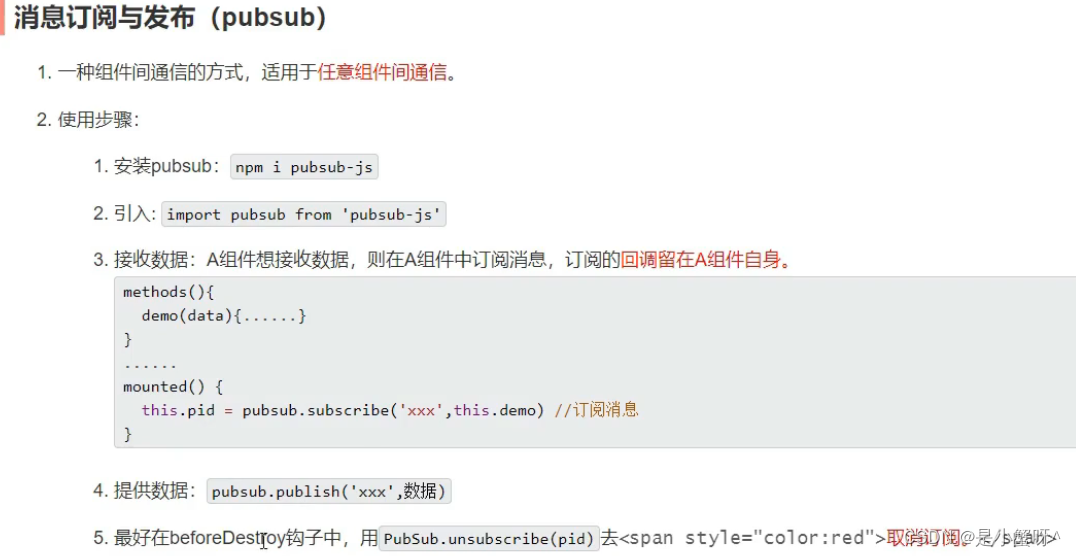
1.安装pubsub:npm i pubsub-js
2.引入:import pubsub from 'pubsub-js'
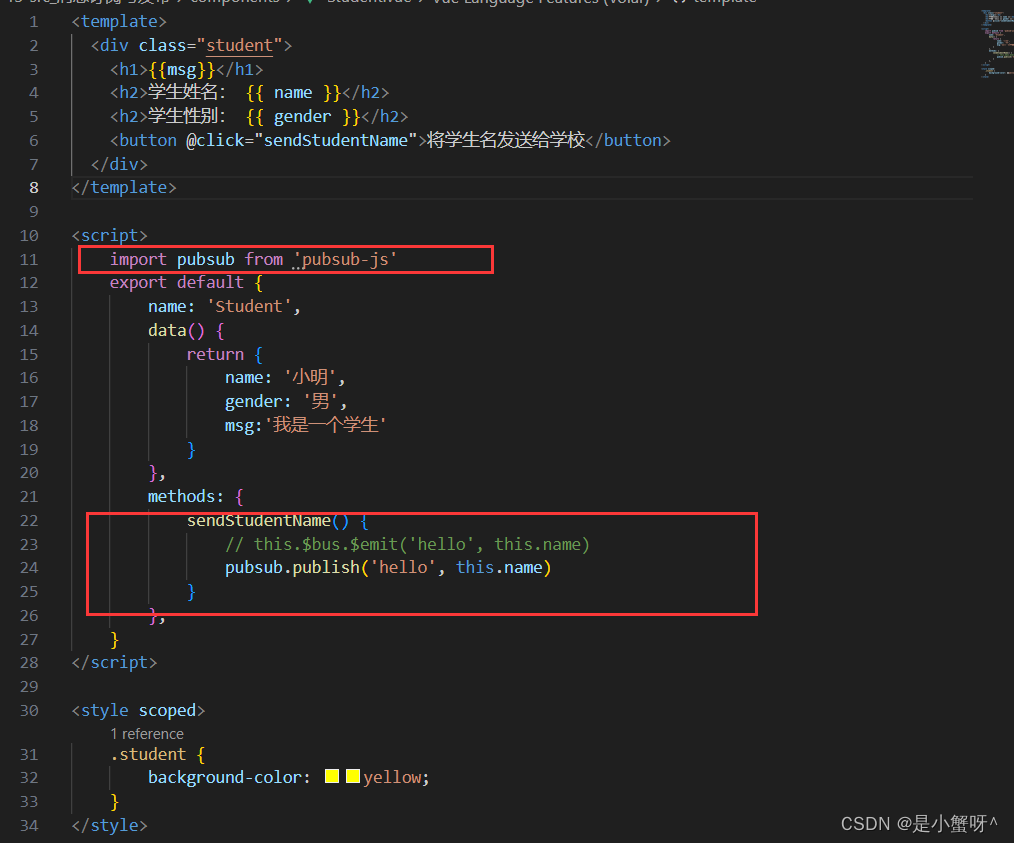
3.发送数据:
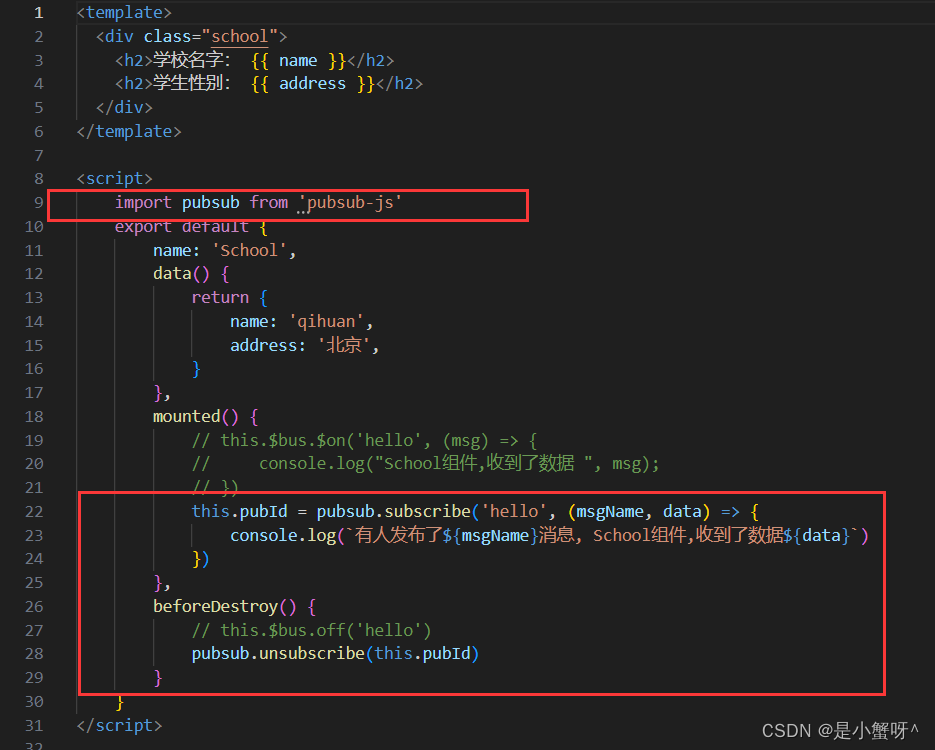
4.接收数据:
总结:
相关文章:

VueCLI核心知识3:全局事件总线、消息订阅与发布
这两种方式都可以实现任意两个组件之间的通信 1 全局事件总线 1.安装全局事件总线 import Vue from vue import App from ./App.vueVue.config.productionTip false/* 1.第一种写法 */ // const Demo Vue.extend({}) // const d new Demo()// Vue.prototype.x d // 把Dem…...

Redis中缓存问题
缓存预热 Redis缓存预热是一项关键任务,可帮助提升应用程序的性能和响应速度。在高流量的应用程序中,Redis缓存预热可以加速数据查询和读取,从而改善用户体验。本文将介绍一种快速、稳定的Redis缓存预热方案,并提供相应代码实现。…...
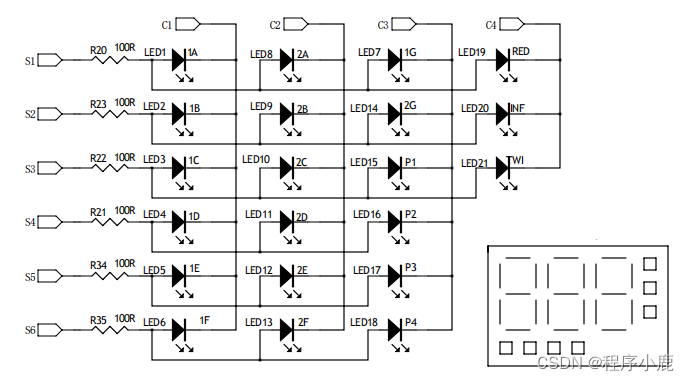
数码管扫描显示-单片机通用模板
数码管扫描显示-单片机通用模板 一、数码管扫描的原理二、display.c的实现1、void Display(void) 各模式界面定义数据2、void BackupRamToDisRam(void)从缓存区刷新显示映射Ram3、void FreshDisplay(void) 映射显示Ram到主控的IO口4、void LcdDisplay_8bit(void) 映射显示Ram到…...
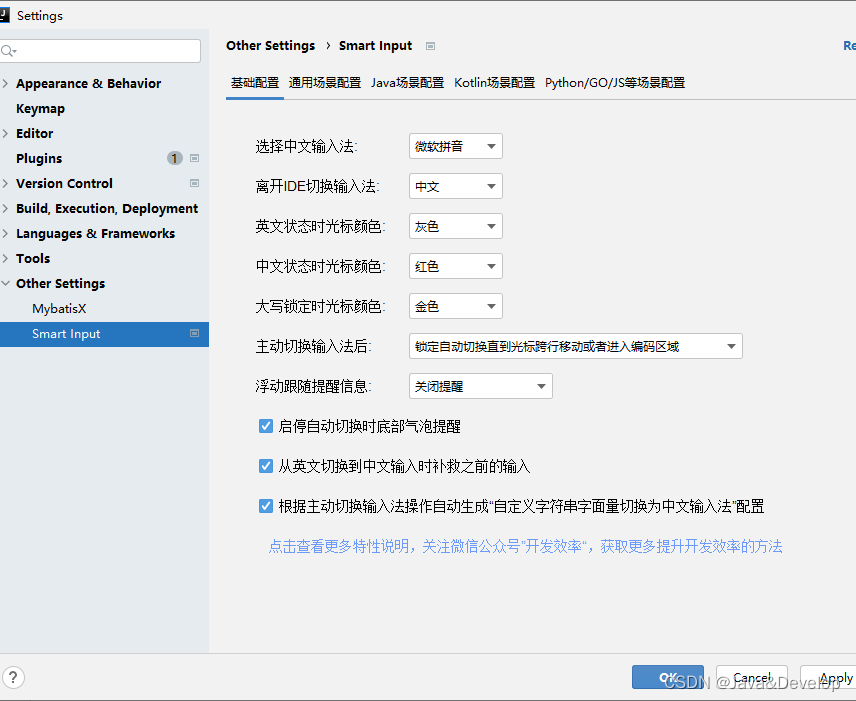
IDEA中的神仙插件——Smart Input (自动切换输入法)
IDEA中的神仙插件——Smart Input (自动切换输入法) 设置 更多功能详见官方文档:Windows版SmartInput使用入门...
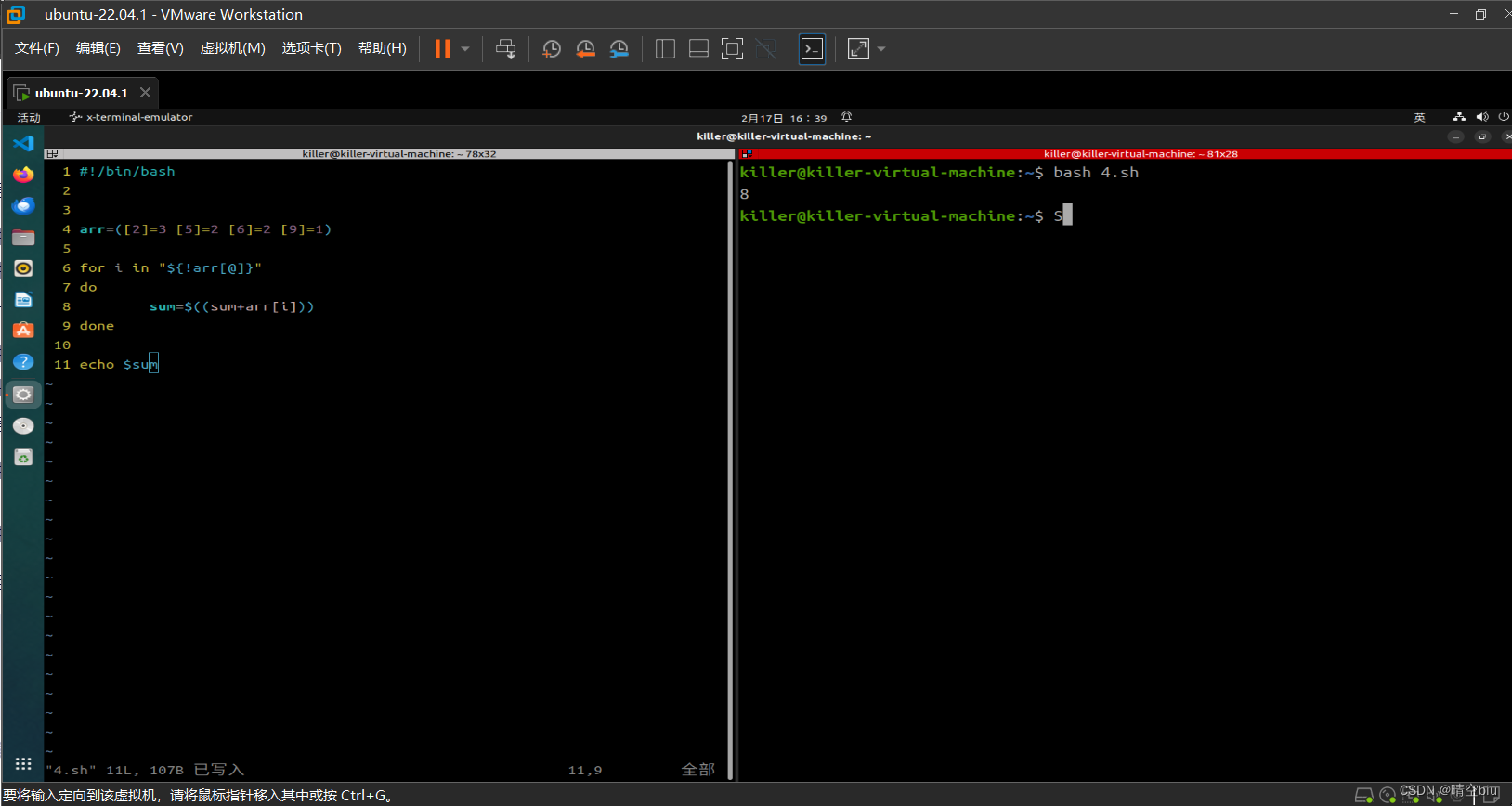
shell编程:求稀疏数组中元素的和(下标不连续)
#!/bin/basharr([2]3 [5]2 [6]2 [9]1)for i in "${!arr[]}" dosum$((sumarr[i])) doneecho $sumBash 脚本中,* 和 符号在数组上下文中有不同的用途。当使用它们来遍历数组时,必须了解它们之间的区别。 * (无前置感叹号 !): 在索引…...

Rust 学习笔记 - 详解数据类型
前言 任何一门编程语言几乎都脱离不了:变量、基本类型、函数、注释、循环、条件判断,这是一门编程语言的语法基础,只有当掌握这些基础语法及概念才能更好的学习 Rust。 标量类型(Scalar Types) 在 Rust 中ÿ…...

构建本地yum源
下载repo数据文件 根据需要修改下载路径和reposync参数 #!/bin/bashlocal_path/repo/remote/rhel9 enabled_repos$(yum repolist enabled | awk NR>3{print $1}) tempfile$(mktemp -t reposync.XXXX)check() {echo "目标目录剩余空间: $(df -h ${local_path} | awk …...
常用的正则表达式,收藏必备!!!
正则表达式是一种强大的文本模式匹配工具,用于在字符串中查找、替换和验证特定模式的文本。下面是一些常用的正则表达式示例: 匹配Email地址: ^[a-zA-Z0-9._%-][a-zA-Z0-9.-]\.[a-zA-Z]{2,}$匹配URL: ^(https?|ftp)://[^\s/$.?#…...

js---webAPI
01 声明变量 js组成: DOM:操作网页内容的,开发页面内容特效和实现用户交互 BOM: DOM树:将 HTML 文档以树状结构直观的表现出来,我们称之为文档树或 DOM 树 文档树直观的体现了标签与标签之间的关系 CSS获取元素的方法 document.querySele…...

git的常用命令有哪些?
Git 是一个流行的分布式版本控制系统,用于跟踪文件的变化、协作开发和管理代码。以下是一些常用的 Git 命令: 创建和克隆仓库: git init:在当前目录初始化一个新的 Git 仓库。git clone <仓库URL>:克隆一个远程仓…...
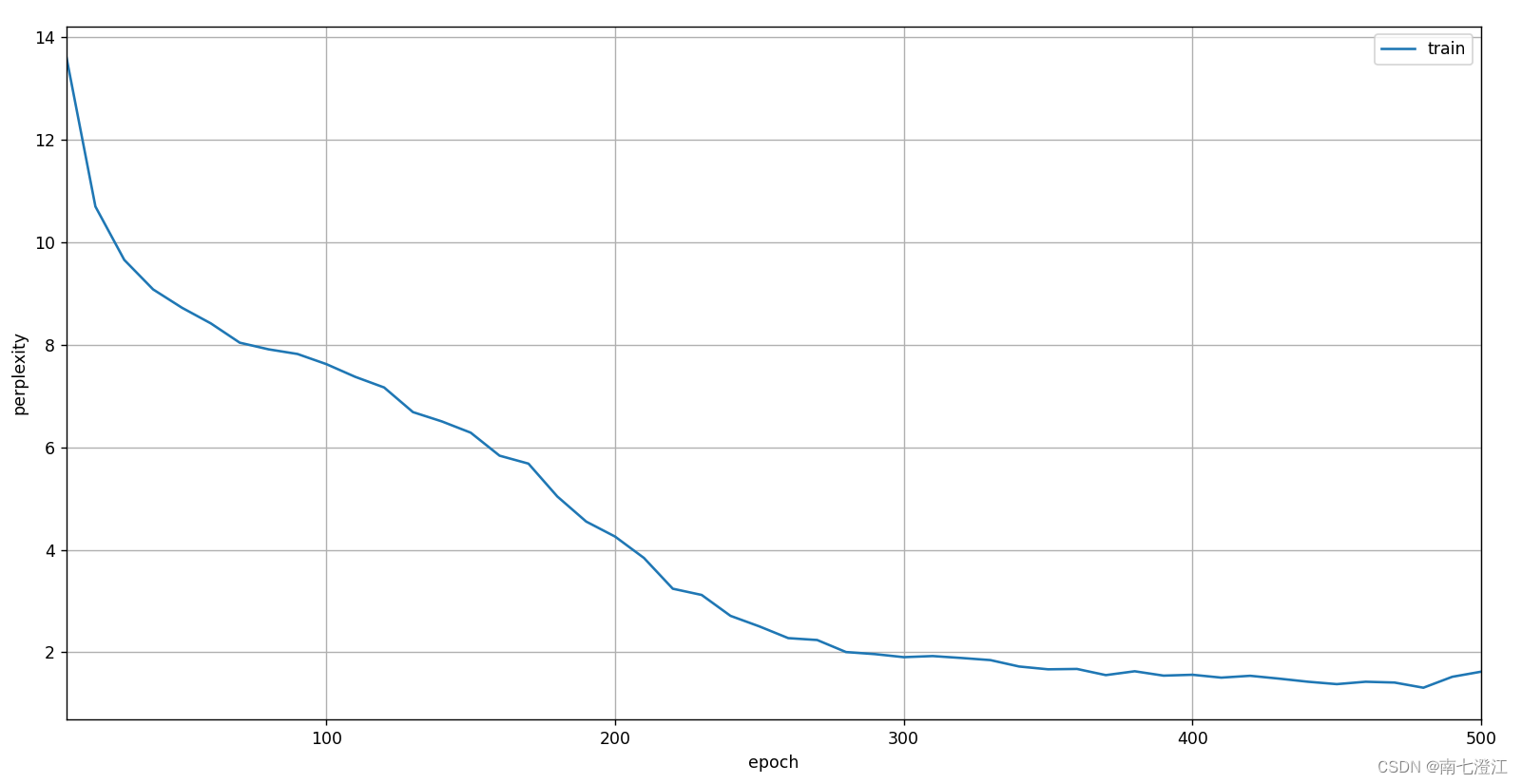
《动手学深度学习(PyTorch版)》笔记8.5
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过&…...
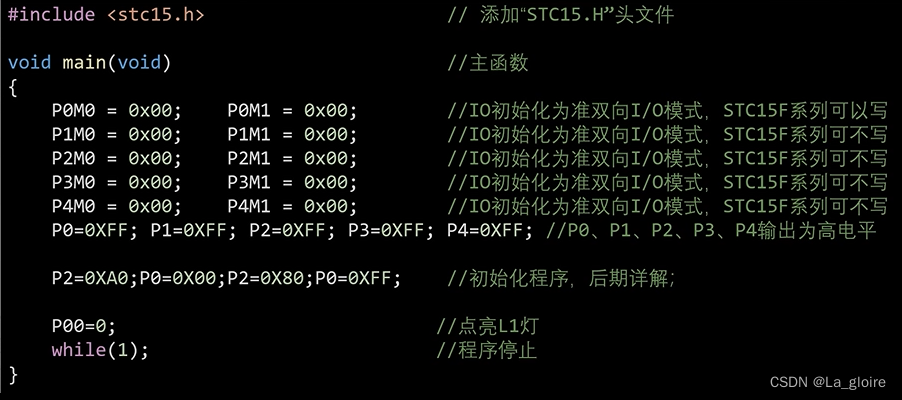
【蓝桥杯单片机入门记录】LED灯(附多个例程)
目录 一、LED灯概述 1.1 LED发光原理 1.2电路原理图 1.3电路实物图 1.4 开发板LED灯原理图 1.4.1共阳极LED灯操控原理(本开发板) (非实际原理图,便于理解版本)由图可以看出,每个LED灯的左边…...

c语言简单json库
文章目录 写在前面头文件源代码使用示例 写在前面 用c语言实现的一个简单json库,极其轻量 仅1个四百多行源码的源文件,和1个头文件 支持对象、数组、数值、字符串类型 github仓库 头文件 对主要的json API的声明 #ifndef ARCOJSON_ARCOJSON_H #defin…...

Linux操作系统基础(七):Linux常见命令(二)
文章目录 Linux常见命令(二) 一、kill命令 二、ifconfig命令 三、clear命令 四、重启与关机命令 五、which命令 六、hostname命令 七、grep命令 八、|管道 九、useradd命令 十、userdel命令 十一、tar命令 十二、su命令 十三、ps命令 Linu…...

进程状态
广义概念: 从广义上来讲,进程分为新建、运行、阻塞、挂起、退出五个状态,其中新建和退出两个状态可以直接理解字面意思。 运行状态: 这里涉及到运行队列的概念,CPU在读取数据的时候,需要把内存中的进程放入…...
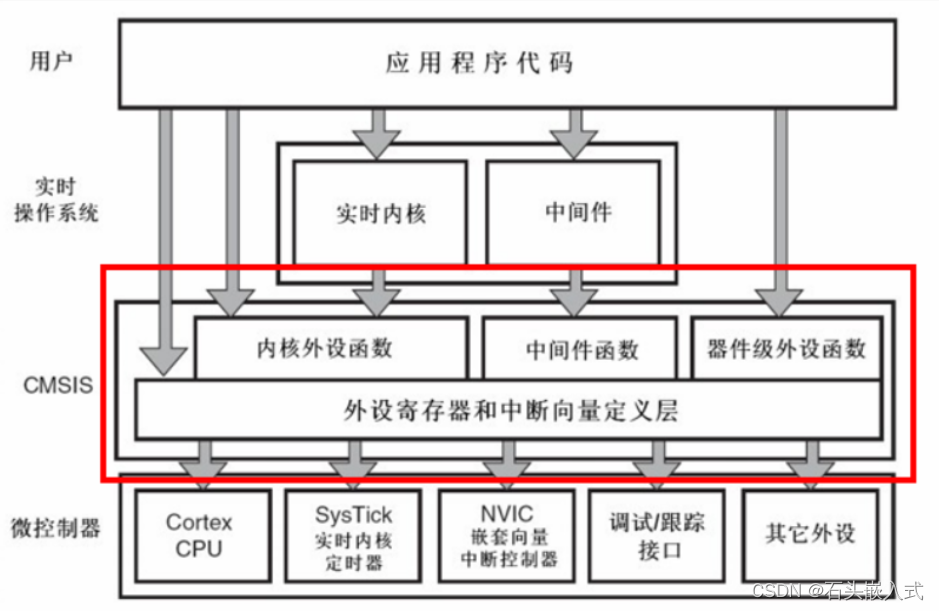
STM32固件库简介与使用指南
1. STM32官方标准固件库简介 STM32官方标准固件库是由STMicroelectronics(ST)提供的一套软件开发工具,旨在简化STM32微控制器的软件开发过程。该固件库提供了丰富的功能和模块,涵盖了STM32微控制器的各种外设,包括但不…...

【开源】SpringBoot框架开发智能教学资源库系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 课程档案模块2.3 课程资源模块2.4 课程作业模块2.5 课程评价模块 三、系统设计3.1 用例设计3.2 数据库设计3.2.1 课程档案表3.2.2 课程资源表3.2.3 课程作业表3.2.4 课程评价表 四、系统展示五、核心代…...

融资项目——获取树形结构的数据
如下图所示,下列数据是一个树形结构数据,行业中包含若干子节点。表的设计如下图,设置了一个id为1的虚拟根节点。(本树形结构带虚拟根节点共三层) 实现逻辑: 延时展示方法,先展现第二层的信息&a…...

Crypto-RSA2
题目:(BUUCTF在线评测 (buuoj.cn)) 已知e,n,dp/(dq),c求明文: 首先有如下公式: dp ≡ d mod (p-1) ,ed ≡ 1 mod φ(n) ,npq ,φ(n)(p-1)(q-1) python代码实现如下: import libnu…...
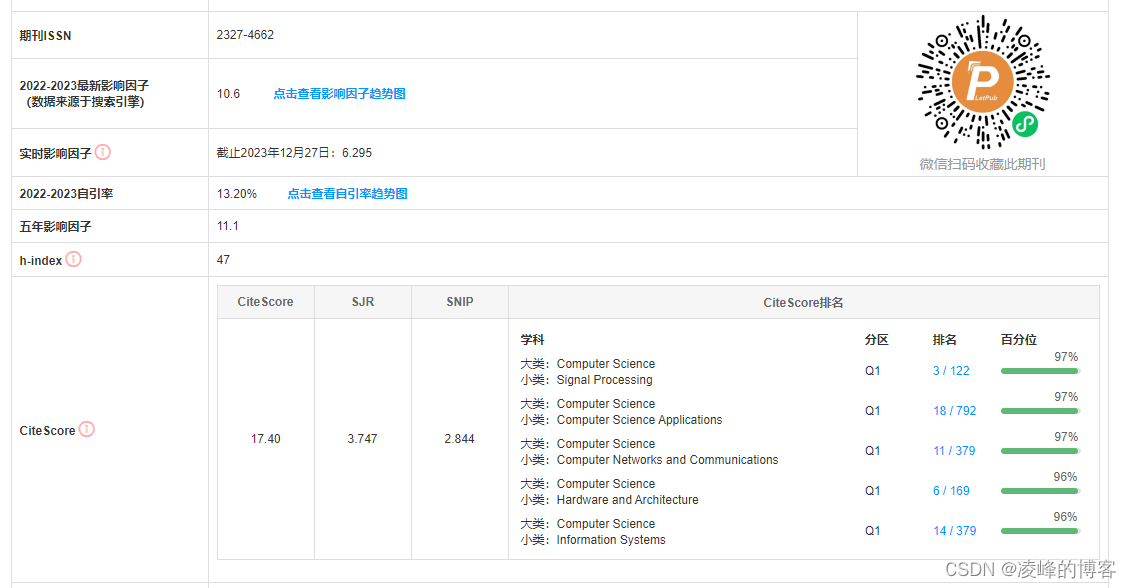
IEEE Internet of Things Journal投稿经验
期刊名:IEEE Internet of Things Journal 期刊分区:中科院一区 Top 影响因子:10.6 投稿状态 (1)2023.11.3,投稿成功,状态为:under review(大u大r)࿱…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
