解线性方程组(二)——Jacobi迭代法求解(C++)
迭代法
相比于直接法求解,迭代法使用多次迭代来逐渐逼近解,其精度比不上直接法,但是其速度会比直接法快很多,计算精度可控,特别适用于求解系数矩阵为大型稀疏矩阵的方程组。
Jacobi迭代法
假设有方程组如下:
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ ⋯ ⋯ a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n \begin{cases} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1\\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2\\ \cdots \qquad \qquad\cdots \qquad \qquad \cdots \\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n=b_n\\ \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯an1x1+an2x2+⋯+annxn=bn
将其转换为矩阵形式
A x ⃗ = b ⃗ A\vec{x}=\vec{b} Ax=b
[ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] [ x 1 x 2 ⋮ x n ] = [ b 1 b 2 ⋮ b n ] \begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{m1}}&{a_{m2}}&{\cdots}&{a_{mn}}\\ \end{bmatrix} \begin{bmatrix} {x_{1}}\\ {x_{2}}\\ {\vdots}\\ {x_{n}}\\ \end{bmatrix}= \begin{bmatrix} {b_{1}}\\ {b_{2}}\\ {\vdots}\\ {b_n} \end{bmatrix} a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn x1x2⋮xn = b1b2⋮bn
对于是否可以使用Jacobi迭代法,需要满足以下条件之一:
- A为行对角优阵,即 ∣ a i i ∣ > ∑ j ≠ i ∣ a i j ∣ ( i = 1 , 2 , ⋯ , n ) |a_{ii}|>\sum_{j \neq i}|a_{ij}|(i=1,2,\cdots,n) ∣aii∣>∑j=i∣aij∣(i=1,2,⋯,n)
- A为行列角优阵,即 ∣ a j j ∣ > ∑ j ≠ i ∣ a i j ∣ ( j = 1 , 2 , ⋯ , n ) |a_{jj}|>\sum_{j \neq i}|a_{ij}|(j=1,2,\cdots,n) ∣ajj∣>∑j=i∣aij∣(j=1,2,⋯,n)
- A的元素满足 ∑ i ≠ j ∣ a i j ∣ ∣ a i i ∣ < 1 ( j , 1 , 2 , ⋯ , n ) \sum_{i \neq j}\frac{|a_{ij}|}{|aii|}<1(j,1,2,\cdots,n) ∑i=j∣aii∣∣aij∣<1(j,1,2,⋯,n)
若矩阵A满足上述条件之一,则可以使用Jacobi迭代法求解方程组。
首先将上述的方程组转为如下形式:
{ x 1 = 1 a 11 ( − a 12 x 2 − ⋯ − a 1 n x n + b 1 ) x 2 = 1 a 22 ( − a 21 x 1 − ⋯ − a 2 n x n + b 2 ) ⋯ ⋯ ⋯ x n = 1 a n n ( − a n 1 x 1 − ⋯ − a n n − 1 x n − 1 + b n ) \begin{cases} x_1=\frac{1}{a_{11}}(-a_{12}x_2-\cdots -a_{1n}x_n+b_1)\\ x_2=\frac{1}{a_{22}}(-a_{21}x_1-\cdots -a_{2n}x_n+b_2)\\ \cdots \qquad \qquad\cdots \qquad \qquad \cdots \\ x_n=\frac{1}{a_{nn}}(-a_{n1}x_1-\cdots -a_{nn-1}x_{n-1}+b_n)\\ \end{cases} ⎩ ⎨ ⎧x1=a111(−a12x2−⋯−a1nxn+b1)x2=a221(−a21x1−⋯−a2nxn+b2)⋯⋯⋯xn=ann1(−an1x1−⋯−ann−1xn−1+bn)
写成矩阵形式可以得到Jacobi迭代式:
( D + L + u ) x ⃗ = b ⃗ D x ⃗ = − ( L + U ) x ⃗ + b ⃗ x ⃗ ( k + 1 ) = − D − 1 ( L + U ) x ⃗ ( k ) + D − 1 b ⃗ (D+L+u)\vec{x}=\vec{b}\\ D\vec{x}=-(L+U)\vec{x}+\vec{b}\\ \vec{x}^{(k+1)}=-D^{-1}(L+U)\vec{x}^{(k)}+D^{-1}\vec{b} (D+L+u)x=bDx=−(L+U)x+bx(k+1)=−D−1(L+U)x(k)+D−1b
其中 D D D为对角矩阵, L L L为下三角矩阵- D D D, U U U为上三角矩阵- U U U, D + L + U D+L+U D+L+U为矩阵A。

代码实现
由于这个过程涉及大量的矩阵操作,整个算法分为两个源文件:Matrix.cpp实现矩阵操作,main.cpp实现Jacobi迭代法。
首先是Matrix.cpp的代码,其中矩阵求逆的原理参考:
#include <Matrix.h>
#include <iostream>
#include <cmath>
//矩阵与向量相乘,输入矩阵A,向量b,运算结果result和维数n
void matrix_multiply_vector(double **A,double *b,double * result,int n)
{for(int i=0;i<n;i++){result[i]=0.0;for(int j=0;j<n;j++){result[i]+=A[i][j]*b[j];}}
}
//矩阵乘法
void matrix_multiply_matrix(double **A,double **B,double **result,int n)
{for(int i=0;i<n;i++){for(int j=0;j<n;j++){result[i][j]=0.0;for(int k=0;k<n;k++){result[i][j]+=A[i][k]*B[k][j];}}}
}
//矩阵加减法
void matrix_add_matrix(double **A,double **B,double **result,int n,bool isAdd)
{for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(isAdd){result[i][j]=A[i][j]+B[i][j];}else{result[i][j]=A[i][j]-B[i][j];}}}
}
//向量的加减法
void vactor_add_vector(double *A,double *B,double *result,int n,bool isAdd)
{for(int i=0;i<n;i++){if(isAdd){result[i]=A[i]+B[i];}else{result[i]=A[i]-B[i];}}
}
//判断向量误差范围,只要符合精度即可
bool vector_equal(double *A,double *B,int n,double error)
{for(int i=0;i<n;i++){if(fabs(A[i]-B[i])>error){return false;}}return true;
}
//向量赋值
void vector_copy(double *A,double *B,int n)
{for(int i=0;i<n;i++){B[i]=A[i];}
}
//矩阵初始化
void matrix_init(double **A,int n)
{for(int i=0;i<n;i++){A[i]=new double [n];for(int j=0;j<n;j++){A[i][j]=0.0;}}
}
//判断矩阵A是否有收敛性
bool astringency(double **A,int n)
{double abs_row_sum=0.0;double abs_col_sum=0.0;double the_third_condition=0.0;bool RowOptimalMatrix=true;bool ColOptimalMatrix=true;for(int i=0;i<n;i++)//判断是不是行对角优阵{abs_row_sum=0.0;for(int j=0;j<n;j++){if(i!=j){abs_row_sum+=fabs(A[i][j]);}}if(abs_row_sum>A[i][i])//证明不是行对角优阵{RowOptimalMatrix=false;break;}}for(int j=0;j<n;j++)//判断是不是列对角优阵{abs_col_sum=0.0;for(int i=0;i<n;i++){if(i!=j){abs_col_sum+=fabs(A[i][j]);}}if(abs_col_sum>A[j][j]){ColOptimalMatrix=false;break;}}return ColOptimalMatrix or RowOptimalMatrix;
}
//矩阵交换某两行
void matrix_swap_row(double **A,int i,int j,int n)
{double temp;for(int k=0;k<n;k++){temp=A[i][k];A[i][k]=A[j][k];A[j][k]=temp;}
}
//矩阵第i行=矩阵第i行-矩阵第j行*a
void matrix_minus_inner(double **A,double a,int i,int j,int n)
{for(int k=0;k<n;k++){A[i][k]-=a*A[j][k];}
}
//矩阵求逆
void matrix_inverse(double **A,double **A_inverse,int n)
{double **A_E=new double*[2*n];//构建增广矩阵for(int i=0;i<n;i++){A_E[i]=new double [n*2];for(int j=0;j<n*2;j++){if(j<n){A_E[i][j]=A[i][j];}else if((j-n)==i){A_E[i][j]=1;}else{A_E[i][j]=0;}}}//首先将矩阵化为上三角矩阵for(int i=0;i<n;i++){if(A_E[i][i]==0){for(int k=i+1;k<n;k++){if(A_E[k][i]!=0){matrix_swap_row(A_E,i,k,n*2);break;}}}for(int j=i+1;j<n;j++){matrix_minus_inner(A_E,A_E[j][i]/A_E[i][i],j,i,2*n);}}//判断矩阵是否可逆for(int i=0;i<n;i++){if(A_E[i][i]==0){std::cout<<"矩阵不可逆"<<std::endl;exit(0);}}//将上三角转换为对角矩阵for(int j=1;j<n;j++){for(int i=0;i<j;i++){matrix_minus_inner(A_E,A_E[i][j]/A_E[j][j],i,j,2*n);}}for(int i=0;i<n;i++){for(int j=n;j<2*n;j++){A_inverse[i][j-n]=A_E[i][j]/A_E[i][i];}}
}
main.cpp文件内容如下:
//Jacobi迭代法求解线性方程组
/*
5x1+2x2-2x3=1
x1+4x2+x3=2
x1-2x2+4x3=-1
*/
#include<iostream>
#include<cmath>
#include<Matrix.h>//自定义头文件
using namespace std;
int main()
{int n;cout<<"Enter the matrix dimension A: ";cin>>n;//输入数组维度double **A=new double *[n];cout<<"Enter the coefficient matrix:"<<endl;for(int i=0;i<n;i++){A[i]=new double[n];for(int j=0;j<n;j++){cin>>A[i][j];//每次输入一个数字都用空格隔开,输入样例//1 2 3\enter//4 5 6\enter//7 8 9\enter}}double *b=new double[n];cout<<"Input vectors b: ";for(int i=0;i<n;i++){cin>>b[i];//输入方程组右边的向量,1 2 3\enter}bool isAstringency=astringency(A,n);//判断系数矩阵A是否具有收敛性if(isAstringency){cout<<"矩阵A符合收敛性"<<endl;}else{exit(0);cout<<"矩阵A不符合收敛性"<<endl;}double *x=new double[n];//解向量Xdouble *x_last=new double[n];//上一次的xfor(int i=0;i<n;i++){x[i]=0.0;//初始化x}double **A_L_U=new double*[n];//L+Udouble **A_D_inverse=new double*[n];//D的逆for(int i=0;i<n;i++){A_D_inverse[i]=new double [n];A_L_U[i]=new double [n];for(int j=0;j<n;j++){if(i==j){A_L_U[i][j]=0.0;A_D_inverse[i][j]=1.0/A[i][j];//对角矩阵的逆为其倒数}else{A_L_U[i][j]=A[i][j];A_D_inverse[i][j]=0.0;}}}double **B=new double *[n];//公式前半段的矩阵matrix_init(B,n);matrix_multiply_matrix(A_D_inverse,A_L_U,B,n);//求D^(-1)(L+U)double *f=new double[n];matrix_multiply_vector(A_D_inverse,b,f,n);//求取D^-1 * bdouble *temp1=new double[n];do{vector_copy(x,x_last,n);matrix_multiply_vector(B,x_last,temp1,n);//计算公式前半段vactor_add_vector(f,temp1,x,n,false);}while(vector_equal(x,x_last,n,1e-6)==false);//判断向量在误差范围内相等cout<<"运行结果为:"<<endl;for(int i=0;i<n;i++){cout<<x[i]<<" ";}system("pause");return 0;
}
结果分析
代码运行结果如下:

当下一次的迭代结果与上一次的迭代结果的最大相差值小于1e-6时,认为迭代已经收敛,输出结果即可(当然也可以换成其它结束迭代方法,如:判断两个向量之差的二范数)。
与直接使用克拉默法则计算准确的解以及matlab计算结果比较,不难发现其 x 1 x_1 x1和 x 3 x_3 x3均不为0,只是是一个在我们设定的误差范围内接近0的数,符合迭代法的解的性质,只能在设定的误差范围内得到一个近似的解。
相关文章:

解线性方程组(二)——Jacobi迭代法求解(C++)
迭代法 相比于直接法求解,迭代法使用多次迭代来逐渐逼近解,其精度比不上直接法,但是其速度会比直接法快很多,计算精度可控,特别适用于求解系数矩阵为大型稀疏矩阵的方程组。 Jacobi迭代法 假设有方程组如下…...
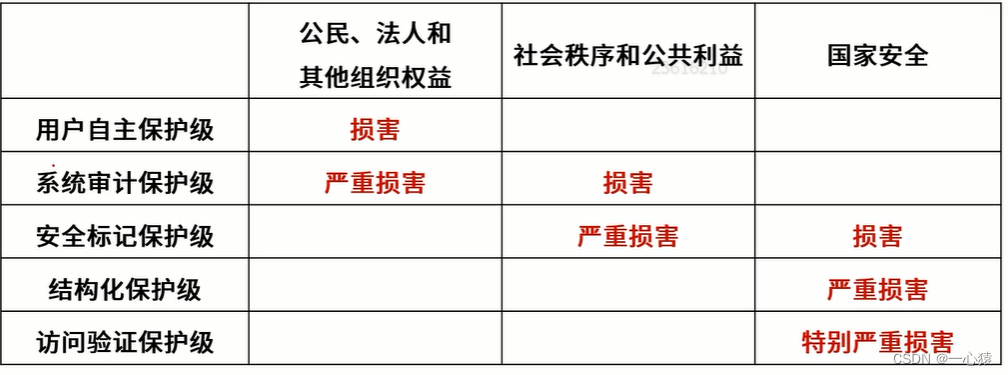
信息安全技术基础知识
一、考点分布 信息安全基础(※※)信息加密解密技术(※※※)密钥管理技术(※※)访问控制及数字签名技术(※※※)信息安全的保障体系 二、信息安全基础 信息安全包括5个基本要素&#…...

使用Taro开发鸿蒙原生应用——快速上手,鸿蒙应用开发指南
导读 本指南为开发者提供了使用 Taro 框架开发鸿蒙原生应用的快速入门方法。Taro,作为一个多端统一开发框架,让开发者能够使用一套代码同时适配多个平台,包括鸿蒙系统。文章将详细介绍如何配置开发环境,以及如何利用 Taro 的特性…...

C语言指针(初阶)
文章目录 1:内存与地址1.1内存1.2:如何理解编址 2:指针变量与地址2.1:指针变量与解引用操作符2.1.1:指针变量2.1.2:如何拆解指针类型2.1.3:解引用操作符 2.2:指针变量的大小 3:指针变量类型的意义代码1解引用修改前解引用修改后 代码2解引用修改前解引用修改后 4:const修饰指针…...

Python循环语句——for循环的嵌套使用
一、引言 在Python编程中,循环是控制程序流程的重要工具,它允许我们重复执行某段代码,直到满足特定的条件为止。其中,for循环是Python中最常用的循环类型之一。而嵌套循环,即在一个循环内部再嵌套另一个循环ÿ…...

Java创建线程真的有三种方式吗?
(/≧▽≦)/~┴┴ 嗨~我叫小奥 ✨✨✨ 👀👀👀 个人博客:小奥的博客 👍👍👍:个人CSDN ⭐️⭐️⭐️:传送门 🍹 本人24应届生一枚,技术和水平有限&am…...

17-k8s控制器资源-job控制
job控制器:就是一次性任务的pod控制器,pod完成作业后不会重启,其重启策略是:Never 1,job控制器案例描述 启动一个pod,执行完成一个事件,然后pod关闭; 事件:计算π的值&a…...
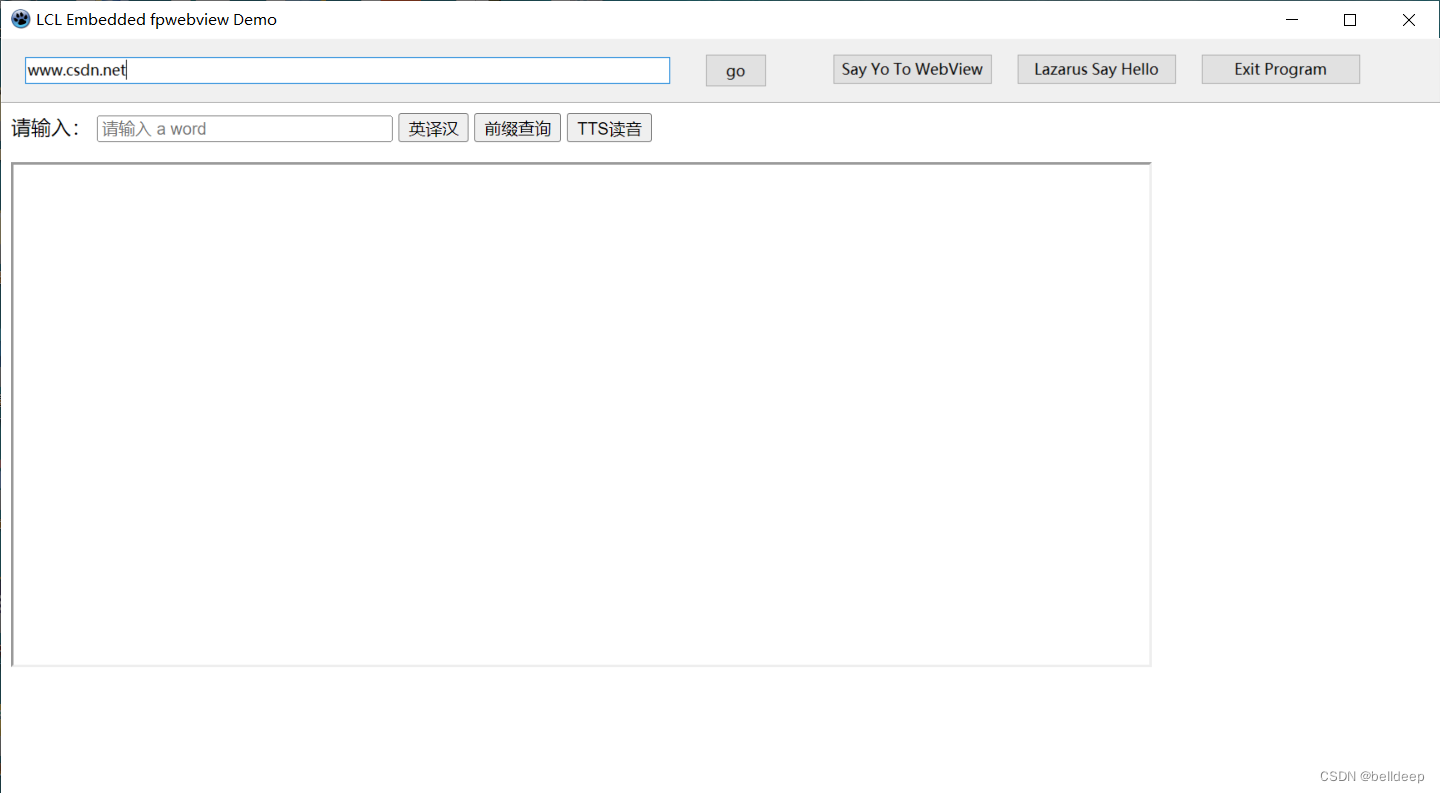
lazarus:LCL 嵌入 fpwebview 组件,做一个简单浏览器
从 https://github.com/PierceNg/fpwebview 下载 fpwebview-master.zip 简单易用。 先请看 \fpwebview-master\README.md cd \lazarus\projects\fpwebview-master\demo\lclembed 修改 lclembed.lpr 如下,将 fphttpapp. 注释掉,因为我用不上 a simple…...
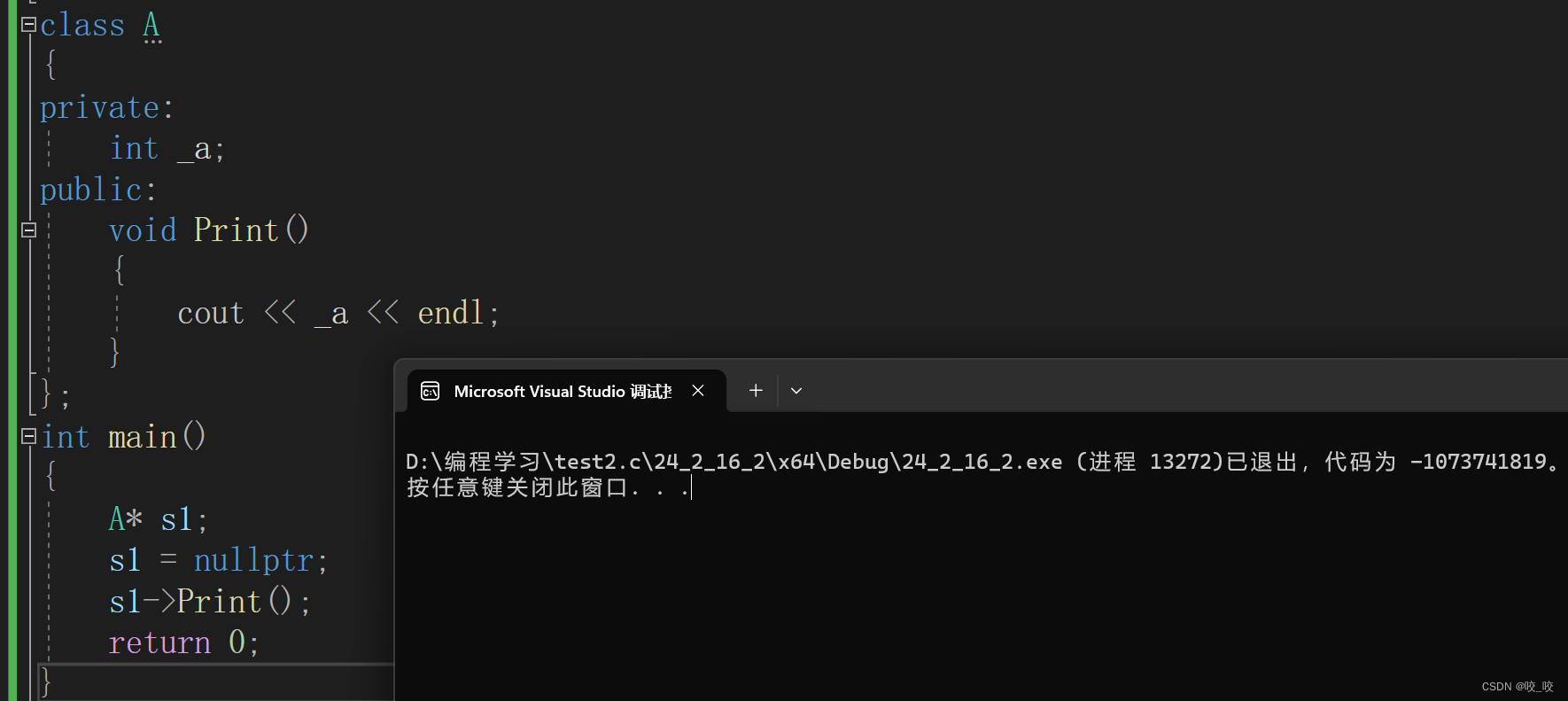
c++类和对象新手保姆级上手教学(上)
前言: c其实顾名思义就是c语言的升级版,很多刚学c的同学第一感觉就是比c语言难学很多,其实没错,c里的知识更加难以理解可以说杂且抽象,光是类和对象,看起来容易,但想完全吃透,真的挺…...

可变参数(c/c++)
目录 一、C语言版本 二、C的实现方法 2.1数据包 2.2sizeof...运算符 2.3可变参数模板的使用 2.4emplace_back() 有时候我们在编写函数时,可能不知道要传入的参数个数,类型 。比如我们要实现一个叠加函数,再比如c语言中的printf,c中的emp…...

【数据结构】图
文章目录 图1.图的两种存储结构2.图的两种遍历方式3.最小生成树的两种算法(无向连通图一定有最小生成树)4.单源最短路径的两种算法5.多源最短路径 图 1.图的两种存储结构 1. 图这种数据结构相信大家都不陌生,实际上图就是另一种多叉树&…...
32.3K Star,再见 Postman,这款开源 API 客户端更香
Hi,骚年,我是大 G,公众号「GitHub指北」会推荐 GitHub 上有趣有用的项目,一分钟 get 一个优秀的开源项目,挖掘开源的价值,欢迎关注。 使用 API 工具来调试接口是后端开发经常会使用的,之前一直…...

Python循环语句——continue和break
一、引言 在Python编程中,循环是常见的控制流语句,它允许我们重复执行一段代码,直到满足某个条件为止。而在循环中,continue和break是两个非常重要的控制语句,它们可以帮助我们更加灵活地控制循环的行为。 二、contin…...

C++面向对象程序设计-北京大学-郭炜【课程笔记(三)】
C面向对象程序设计-北京大学-郭炜【课程笔记(三)】 1、构造函数(constructor)1.1、基本概念 2、赋值构造函数2.1、基本概念2.1、复制构造函数起作用的三种情况2.2、常引用参数的使用 3、类型转换构造函数3.1、什么事类型转换构造函…...
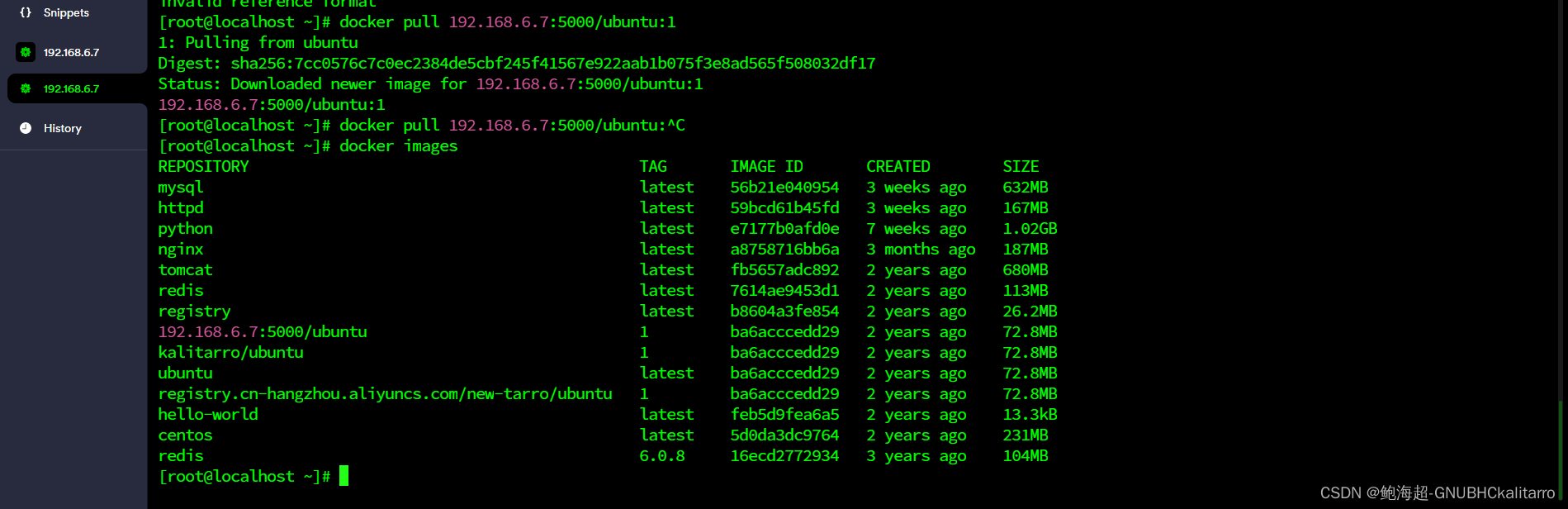
Linux:搭建docker私有仓库(registry)
当我们内部需要存储镜像时候,官方提供了registry搭建好直接用,废话少说直接操作 1.下载安装docker 在 Linux 上安装 Docker Desktop |Docker 文档https://docs.docker.com/desktop/install/linux-install/安装 Docker 引擎 |Docker 文档https://docs.do…...

用HTML、CSS和JS打造绚丽的雪花飘落效果
目录 一、程序代码 二、代码原理 三、运行效果 一、程序代码 <!DOCTYPE html> <html><head><meta http-equiv"Content-Type" content"text/html; charsetGBK"><style>* {margin: 0;padding: 0;}#box {width: 100vw;heig…...

订餐|网上订餐系统|基于springboot的网上订餐系统设计与实现(源码+数据库+文档)
网上订餐系统目录 目录 基于springboot的网上订餐系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、用户功能模块的实现 (1)用户注册界面 (2)用户登录界面 (3)菜品详情界面 (…...

从零开始学howtoheap:解题西湖论剑Storm_note
how2heap是由shellphish团队制作的堆利用教程,介绍了多种堆利用技术,后续系列实验我们就通过这个教程来学习。环境可参见从零开始配置pwn环境:从零开始配置pwn环境:从零开始配置pwn环境:优化pwn虚拟机配置支持libc等指…...

Rust 基本环境安装
rust 基本介绍请看上一篇文章:rust 介绍 rustup 介绍 rustup 是 Rust 语言的安装器和版本管理工具。通过 rustup,可以轻松地安装 Rust 编译器(rustc)、标准库和文档。它也允许你切换不同的 Rust 版本或目标平台,以及…...
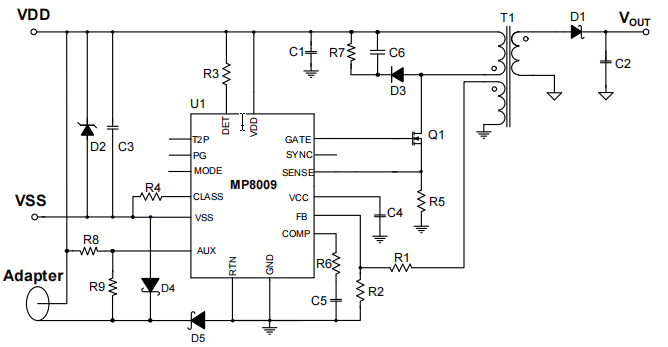
【电源】POE系统供电原理(二)
转载本博客文章,请注明出处 上一篇文章中,有提到POE系统工作原理及动态检测机制,下面我们继续介绍受电端PD技术及原理。POE供电系统包含PSE、PD及互联接口部分组成,如下图所示。 图1 POE供电系统 PSE控制器的主要作用ÿ…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
