数据分析(一) 理解数据
1. 描述性统计(summary)
对于一个新数据集,首先通过观察来熟悉它,可以打印数据相关信息来大致观察数据的常规特点,比如数据规模(行数列数)、数据类型、类别数量(变量数目、取值范围)、缺失值、异常值等等。然后通过描述性统计来了解数据的统计特性、属性间关联关系、属性与标签的关联关系等。
数据集一般是按照行列组织的,每行代表一个实例,每列代表一个属性。
import pandas as pd
import sys
import numpy as np
import pylab
import matplotlib.pyplot as plt
data = pd.read_csv(r"C:\work\PycharmProjects\machine_learning\filename.csv", index_col=0)
# summary
nrow, ncol = data.shape
print(f"行数:{nrow}, 列数:{ncol}")
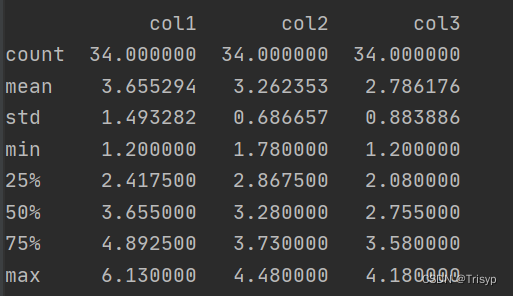
summary = data.describe()
print(summary)
# 箱线图
data_array = data.iloc[:, :3].values
pylab.boxplot(data_array)
plt.xlabel("Attribute Index")
plt.ylabel(("Quartile Ranges"))
pylab.show()
# 标准化后的箱线图
dataNormalized = data.iloc[:, :3]
for i in range(2):
mean = summary.iloc[1, i]
sd = summary.iloc[2, i]
dataNormalized.iloc[:, i:(i + 1)] = (dataNormalized.iloc[:, i:(i + 1)] - mean) / sd
array3 = dataNormalized.values
pylab.boxplot(array3)
plt.xlabel("Attribute Index")
plt.ylabel(("Quartile Ranges - Normalized "))
pylab.show()
colArray = np.array(list(data.iloc[:, 0]))
colMean = np.mean(colArray)
colsd = np.std(colArray)
sys.stdout.write("Mean = " + '\t' + str(colMean) + '\t\t' +
"Standard Deviation = " + '\t ' + str(colsd) + "\n")
# calculate quantile boundaries(四分位数边界)
ntiles = 4
percentBdry = []
for i in range(ntiles + 1):
percentBdry.append(np.percentile(colArray, i * (100) / ntiles))
sys.stdout.write("\nBoundaries for 4 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")
# run again with 10 equal intervals(十分位数边界)
ntiles = 10
percentBdry = []
for i in range(ntiles + 1):
percentBdry.append(np.percentile(colArray, i * (100) / ntiles))
sys.stdout.write("Boundaries for 10 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")
# The last column contains categorical variables(标签变量)
colData = list(data.iloc[:, 1])
unique = set(colData)
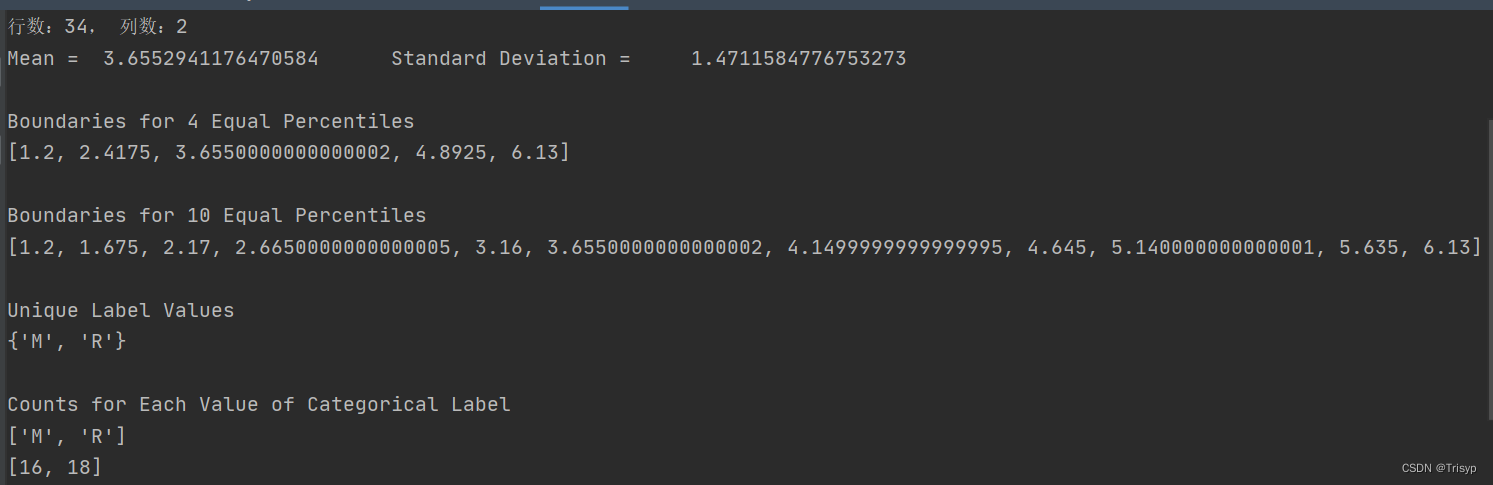
sys.stdout.write("Unique Label Values \n")
print(unique)
# count up the number of elements having each value
catDict = dict(zip(list(unique), range(len(unique))))
catCount = [0] * 2
for elt in colData:
catCount[catDict[elt]] += 1
sys.stdout.write("\nCounts for Each Value of Categorical Label \n")
print(list(unique))
print(catCount)
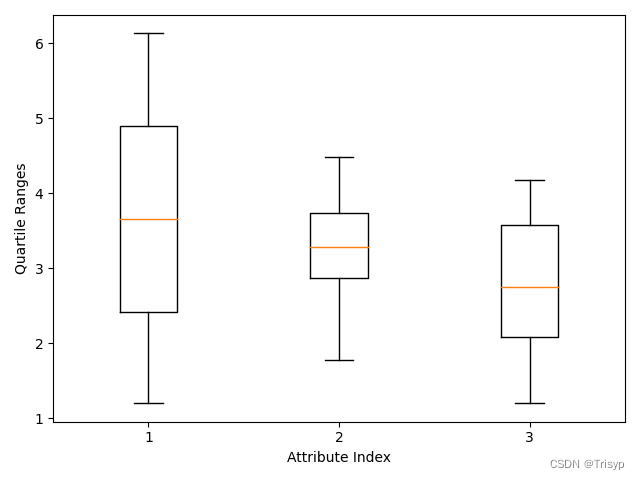
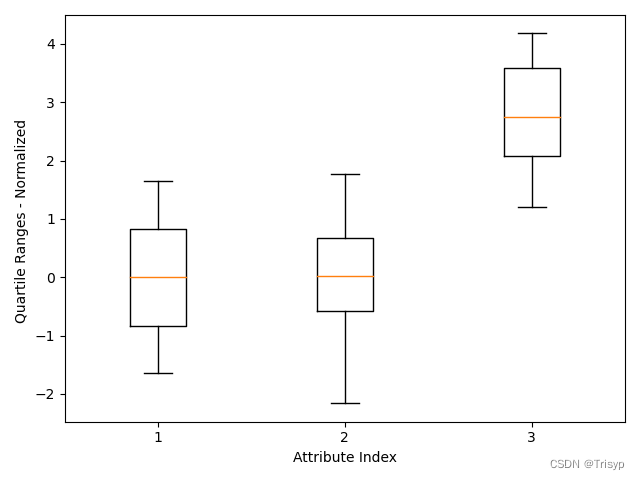
图中显示了一个小长方形,有一个红线穿过它。红线代表此列数据的中位数(第 50 百分位数),长方形的顶和底分别表示第 25 百分位数和第 75 百分位数(或者第一四分位数、第三四分位数)。在盒子的上方和下方有小的水平线,叫作盒须(whisker)。它们分别据盒子的上边和下边是四分位间距的 1.4 倍,四分位间距就是第 75 百分位数和第 25 百分位数之间的距离,也就是从盒子的顶边到盒子底边的距离。也就是说盒子上面的盒须到盒子顶边的距离是盒子高度的 1.4 倍。这个盒须的 1.4 倍距离是可以调整的(详见箱线图的相关文档)。在有些情况下,盒须要比 1.4 倍距离近,这说明数据的值并没有扩散到原定计算出来的盒须的位置。在这种情况下,盒须被放在最极端的点上。在另外一些情况下,数据扩散到远远超出计算出的盒须的位置(1.4 倍盒子高度的距离),这些点被认为是异常点。
2. 二阶统计信息(distribute,corr)
# 分位数图
import scipy.stats as stats
import pylab
stats.probplot(colArray, dist="norm", plot=pylab)
pylab.show()

如果此数据服从高斯分布,则画出来的点应该是接近一条直线。
# 属性间关系散点图
import matplotlib.pyplot as plt
data_row1 = data.iloc[0, :3]
data_row2 = data.iloc[1, :3]
plt.scatter(data_row1, data_row2)
plt.xlabel("1st Attribute")
plt.ylabel(("2nd Attribute"))
plt.show()
# 属性和标签相关性散点图
from random import uniform
target = []
for i in range(len(colData)):
if colData[i] == 'R': # R用1代表, M用0代表
target.append(1)
else:
target.append(0)
plt.scatter(data_row1, target)
plt.xlabel("Attribute Value")
plt.ylabel("Target Value")
plt.show()
target = []
for i in range(len(colData)):
if colData[i] == 'R': # R用1代表, M用0代表
target.append(1+uniform(-0.1, 0.1))
else:
target.append(0+uniform(-0.1, 0.1))
plt.scatter(data_row1, target, alpha=0.5, s=120) # 透明度50%
plt.xlabel("Attribute Value")
plt.ylabel("Target Value")
plt.show()

第二个图绘制时取 alpha=0.5,这样这些点就是半透明的。那么在散点图中若多个点落在一个位置就会形成一个更黑的区域。

# 关系矩阵及其热图
corMat = pd.DataFrame(data.corr())
plt.pcolor(corMat)
plt.show()

属性之间如果完全相关(相关系数 =1)意味着数据可能有错误,如同样的数据录入两次。多个属性间的相关性很高(相关系数 >0.7),即多重共线性(multicollinearity),往往会导致预测结果不稳定。属性与标签的相关性则不同,如果属性和标签相关,则通常意味着两者之间具有可预测的关系
# 平行坐标图
minRings = summary.iloc[3, 2] # summary第3行为min
maxRings = summary.iloc[7, 2] # summary第7行为max
for i in range(nrow):
# plot rows of data as if they were series data
dataRow = data.iloc[i, :3]
labelColor = (data.iloc[i, 2] - minRings) / (maxRings - minRings)
dataRow.plot(color=plt.cm.RdYlBu(labelColor), alpha=0.5)
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
plt.show()
# 对数变换后平行坐标图
meanRings = summary.iloc[1, 2]
sdRings = summary.iloc[2, 2]
for i in range(nrow):
dataRow = data.iloc[i, :3]
normTarget = (data.iloc[i, 2] - meanRings) / sdRings
labelColor = 1.0 / (1.0 + np.exp(-normTarget))
dataRow.plot(color=plt.cm.RdYlBu(labelColor), alpha=0.5)
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
plt.show()
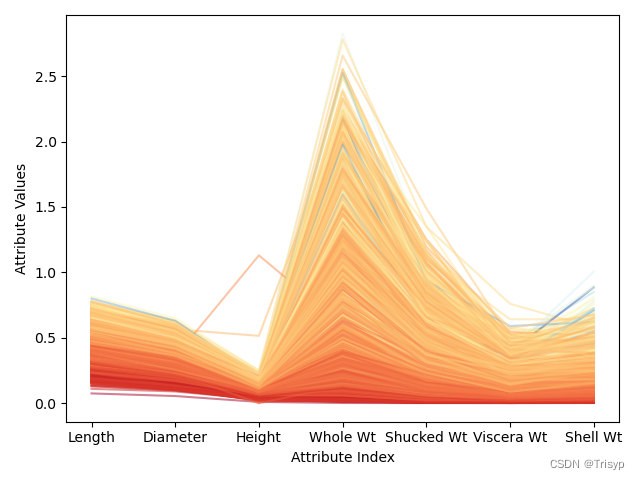
在属性值相近的地方,折线的颜色也比较接近,则会集中在一起。这些相关性都暗示可以构建相当准确的预测模型。相反,有些微弱的蓝色折线与深橘色的区域混合在一起,说明有些实例可能很难正确预测。
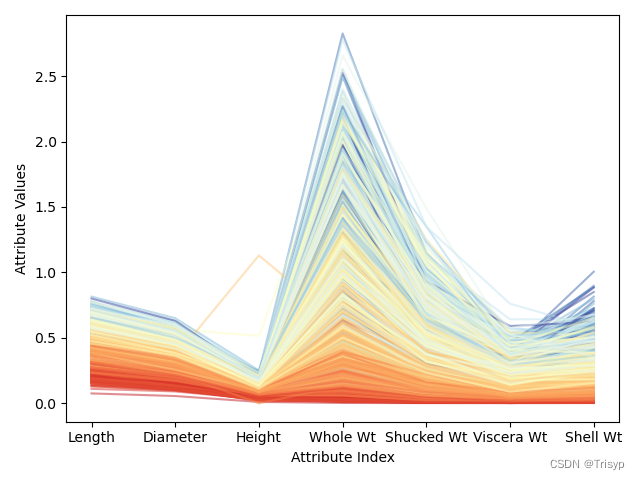
转换后可以更充分地利用颜色标尺中的各种颜色。注意到针对某些个属性,有些深蓝的线(对应年龄大的品种)混入了浅蓝线的区域,甚至是黄色、亮红的区域。这意味着,当该属性值较大时,仅仅这些属性不足以准确地预测出鲍鱼的年龄。好在其他属性可以很好地把深蓝线区分出来。这些观察都有助于分析预测错误的原因。
3. 完整代码(code)
import pandas as pd
import sys
import numpy as np
import pylab
import matplotlib.pyplot as pltdata = pd.read_csv(r"C:\work\PycharmProjects\machine_learning\filename.csv", index_col=0)nrow, ncol = data.shape
print(f"行数:{nrow}, 列数:{ncol}")
summary = data.describe()
print(summary)data_array = data.iloc[:, :3].values
pylab.boxplot(data_array)
plt.xlabel("Attribute Index")
plt.ylabel(("Quartile Ranges"))
pylab.show()dataNormalized = data.iloc[:, :3]
for i in range(2):mean = summary.iloc[1, i]sd = summary.iloc[2, i]dataNormalized.iloc[:, i:(i + 1)] = (dataNormalized.iloc[:, i:(i + 1)] - mean) / sdarray3 = dataNormalized.values
pylab.boxplot(array3)
plt.xlabel("Attribute Index")
plt.ylabel(("Quartile Ranges - Normalized "))
pylab.show()colArray = np.array(list(data.iloc[:, 0]))
colMean = np.mean(colArray)
colsd = np.std(colArray)
sys.stdout.write("Mean = " + '\t' + str(colMean) + '\t\t' +"Standard Deviation = " + '\t ' + str(colsd) + "\n")# calculate quantile boundaries(四分位数边界)
ntiles = 4
percentBdry = []
for i in range(ntiles + 1):percentBdry.append(np.percentile(colArray, i * (100) / ntiles))sys.stdout.write("\nBoundaries for 4 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")# run again with 10 equal intervals(十分位数边界)
ntiles = 10
percentBdry = []
for i in range(ntiles + 1):percentBdry.append(np.percentile(colArray, i * (100) / ntiles))
sys.stdout.write("Boundaries for 10 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")# The last column contains categorical variables(标签变量)
colData = list(data.iloc[:, 3])
unique = set(colData)
sys.stdout.write("Unique Label Values \n")
print(unique)# count up the number of elements having each value
catDict = dict(zip(list(unique), range(len(unique))))
catCount = [0] * 2
for elt in colData:catCount[catDict[elt]] += 1
sys.stdout.write("\nCounts for Each Value of Categorical Label \n")
print(list(unique))
print(catCount)# 分位数图
import scipy.stats as statsstats.probplot(colArray, dist="norm", plot=pylab)
pylab.show()# 属性间关系散点图
data_row1 = data.iloc[:, 0]
data_row2 = data.iloc[:, 1]
plt.scatter(data_row1, data_row2)
plt.xlabel("1st Attribute")
plt.ylabel(("2nd Attribute"))
plt.show()# 属性和标签相关性散点图
from random import uniformtarget = []
for i in range(len(colData)):if colData[i] == 'R': # R用1代表, M用0代表target.append(1)else:target.append(0)
plt.scatter(data_row1, target)
plt.xlabel("Attribute Value")
plt.ylabel("Target Value")
plt.show()target = []
for i in range(len(colData)):if colData[i] == 'R': # R用1代表, M用0代表target.append(1 + uniform(-0.1, 0.1))else:target.append(0 + uniform(-0.1, 0.1))
plt.scatter(data_row1, target, alpha=0.5, s=120) # 透明度50%
plt.xlabel("Attribute Value")
plt.ylabel("Target Value")
plt.show()# 关系矩阵及其热图
corMat = pd.DataFrame(data.corr())
plt.pcolor(corMat)
plt.show()# 平行坐标图
minRings = summary.iloc[3, 2] # summary第3行为min
maxRings = summary.iloc[7, 2] # summary第7行为max
for i in range(nrow):# plot rows of data as if they were series datadataRow = data.iloc[i, :3]labelColor = (data.iloc[i, 2] - minRings) / (maxRings - minRings)dataRow.plot(color=plt.cm.RdYlBu(labelColor), alpha=0.5)
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
plt.show()meanRings = summary.iloc[1, 2]
sdRings = summary.iloc[2, 2]
for i in range(nrow):dataRow = data.iloc[i, :3]normTarget = (data.iloc[i, 2] - meanRings) / sdRingslabelColor = 1.0 / (1.0 + np.exp(-normTarget))dataRow.plot(color=plt.cm.RdYlBu(labelColor), alpha=0.5)
plt.xlabel("Attribute Index")
plt.ylabel(("Attribute Values"))
plt.show()
相关文章:

数据分析(一) 理解数据
1. 描述性统计(summary) 对于一个新数据集,首先通过观察来熟悉它,可以打印数据相关信息来大致观察数据的常规特点,比如数据规模(行数列数)、数据类型、类别数量(变量数目、取值范围…...

什么是 Flet?
什么是 Flet? Flet 是一个框架,允许使用您喜欢的语言构建交互式多用户 Web、桌面和移动应用程序,而无需前端开发经验。 您可以使用基于 Google 的 Flutter 的 Flet 控件为程序构建 UI。Flet 不只是“包装”Flutter 小部件,而是…...
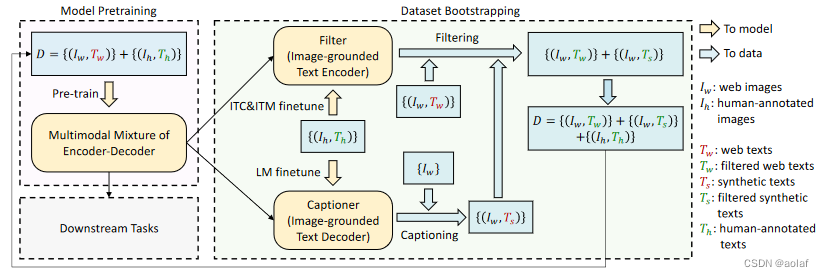
多模态(三)--- BLIP原理与源码解读
1 BLIP简介 BLIP: Bootstrapping Language-Image Pre-training for Unified Vision-Language Understanding and Generation 传统的Vision-Language Pre-training (VLP)任务大多是基于理解的任务或基于生成的任务,同时预训练数据多是从web获…...
掌握高性能SQL的34个秘诀多维度优化与全方位指南
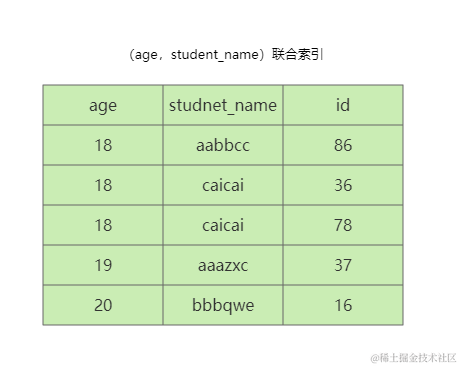
掌握高性能SQL的34个秘诀🚀多维度优化与全方位指南 本篇文章从数据库表结构设计、索引、使用等多个维度总结出高性能SQL的34个秘诀,助你轻松掌握高性能SQL 表结构设计 字段类型越小越好 满足业务需求的同时字段类型越小越好 字段类型越小代表着记录占…...

美国纳斯达克大屏怎么投放:投放完成需要多长时间-大舍传媒Dashe Media
陕西大舍广告传媒有限公司(Shaanxi Dashe Advertising Media Co., Ltd),简称大舍传媒(Dashe Media),是纳斯达克在中国区的总代理(China General Agent)。与纳斯达克合作已经有八年的…...

【MySQL】多表关系的基本学习
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-3oES1ZdkKIklfKzq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…...
Springboot之接入gRPC
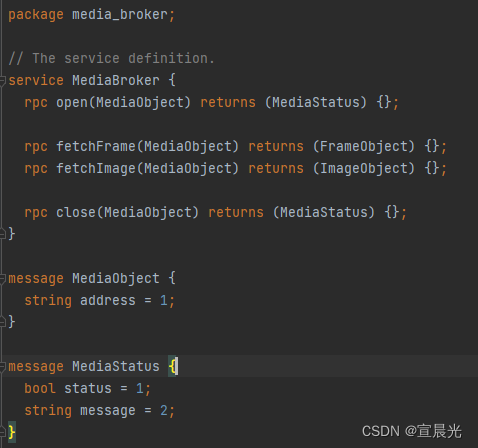
1、maven依赖 <properties><!-- grpc --><protobuf.version>3.5.1</protobuf.version><protobuf-plugin.version>0.6.1</protobuf-plugin.version><grpc.version>1.42.1</grpc.version><os-maven-plugin.version>1.6.0…...

2023年中国数据智能管理峰会(DAMS上海站2023):核心内容与学习收获(附大会核心PPT下载)
随着数字经济的飞速发展,数据已经渗透到现代社会的每一个角落,成为驱动企业创新、提升治理能力、促进经济发展的关键要素。在这样的背景下,2023年中国数据智能管理峰会(DAMS上海站2023)应运而生,汇聚了众多…...
DS:八大排序之堆排序、冒泡排序、快速排序
创作不易,友友们给个三连吧!! 一、堆排序 堆排序已经在博主关于堆的实现过程中详细的讲过了,大家可以直接去看,很详细,这边不介绍了 DS:二叉树的顺序结构及堆的实现-CSDN博客 直接上代码: …...

Sora:继ChatGPT之后,OpenAI的又一力作
关于Sora的报道,相信很多圈内朋友都已经看到了来自各大媒体铺天盖地的宣传了,这次,对于Sora的宣传,绝不比当初ChatGPT的宣传弱。自OpenAI发布了GPT4之后,就已经有很多视频生成模型了,不过这些模型要么生成的…...

阅读笔记(BMSB 2018)Video Stitching Based on Optical Flow
参考文献 Xie C, Zhang X, Yang H, et al. Video Stitching Based on Optical Flow[C]//2018 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB). IEEE, 2018: 1-5. 摘要 视频拼接在计算机视觉中仍然是一个具有挑战性的问题࿰…...

Ubuntu学习笔记-Ubuntu搭建禅道开源版及基本使用
文章目录 概述一、Ubuntu中安装1.1 复制下载安装包路径1.2 将安装包解压到ubuntu中1.3 启动服务1.4 设置开机自启动 二、禅道服务基本操作2.1 启动,停止,重启,查看服务状态2.2 开放端口2.3 访问和登录禅道 卜相机关 卜三命、相万生࿰…...

《苍穹外卖》知识梳理6-缓存商品,购物车功能
苍穹外卖实操笔记六—缓存商品,购物车功能 一.缓存菜品 可以使用redis进行缓存;另外,在实现缓存套餐时可以使用spring cache提高开发效率; 通过缓存数据,降低访问数据库的次数; 使用的缓存逻辑&#…...
[NSSCTF]-Web:[SWPUCTF 2021 新生赛]easy_sql解析
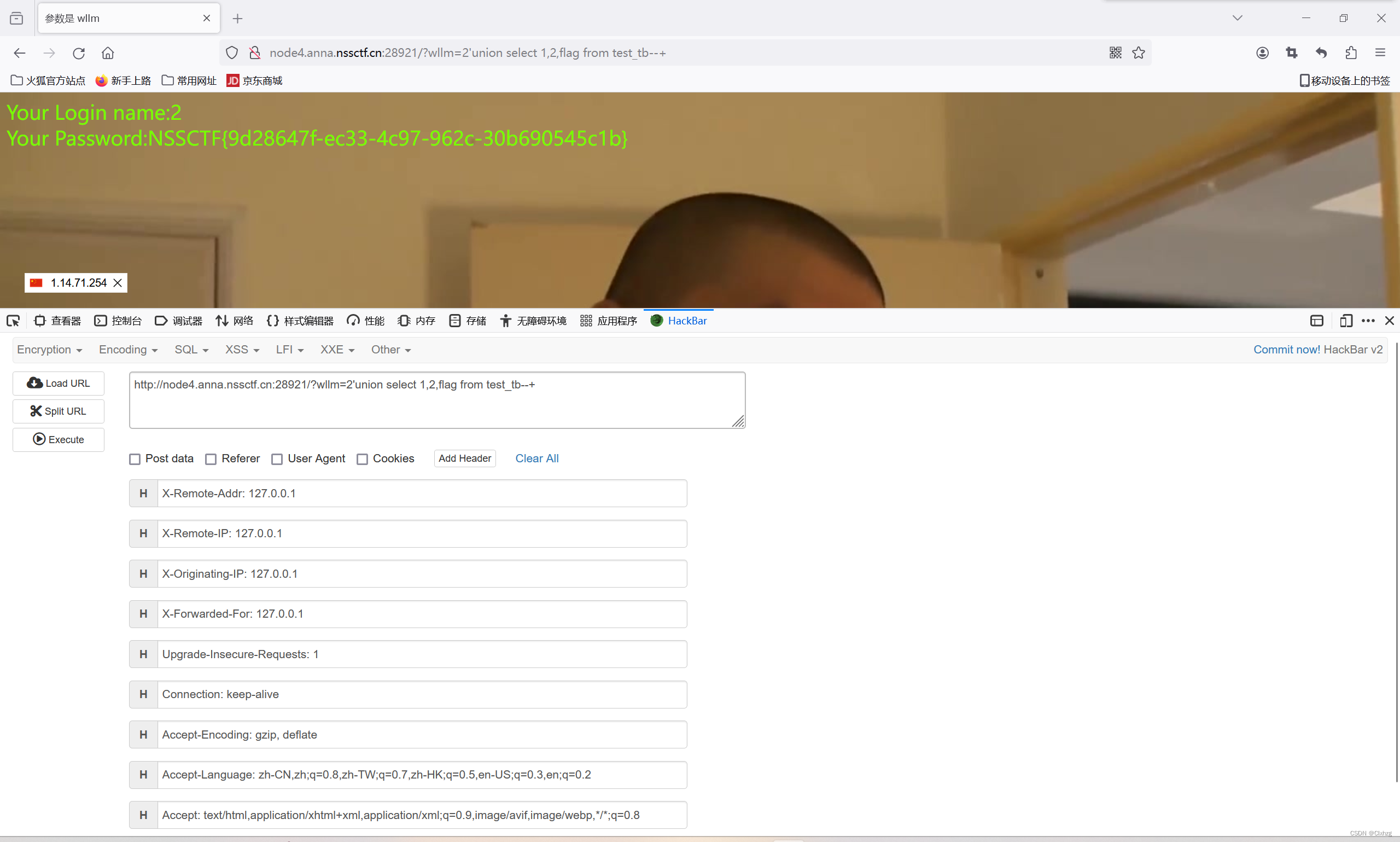
查看网页 有提示,参数是wllm,并且要我们输入点东西 所以,我们尝试以get方式传入 有回显,但似乎没啥用 从上图看应该是字符型漏洞,单引号字符注入 先查看字段数 /?wllm2order by 3-- 没回显 报错了,说明…...

vue3 codemirror yaml文件编辑器插件
需求:前端编写yaml配置文件 ,检查yaml语法 提供语法高亮 。 默认内容从后端接口获取 显示在前端 , 前端在codemirror 插件中修改文件内容 ,并提交修改 后端将提交的内容写入服务器配置文件中 。 codemirror 通过ref 后期编辑器…...
力扣经典题:环形链表的检测与返回
1.值得背的题 /*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/ struct ListNode *detectCycle(struct ListNode *head) {struct ListNode*fasthead;struct ListNode*slowhead;while(fast!NULL&&fast->…...
【web | CTF】BUUCTF [BJDCTF2020]Easy MD5
天命:好像也挺实用的题目,也是比较经典吧 天命:把php的MD5漏洞都玩了一遍 第一关:MD5绕过 先声明一下:这题的MD5是php,不是mysql的MD5,把我搞迷糊了 一进来题目啥也没有,那么就要看…...

spring boot Mybatis Plus分页
文章目录 Mybatis Plus自带分页和PageHelper有什么区别?Mybatis Plus整合PageHelper分页 springboot自定义拦截器获取分页参数spring boot下配置mybatis-plus分页插件单表分页查询自定义sql分页查询PageHelper 参考 Mybatis Plus自带分页和PageHelper有什么区别&…...
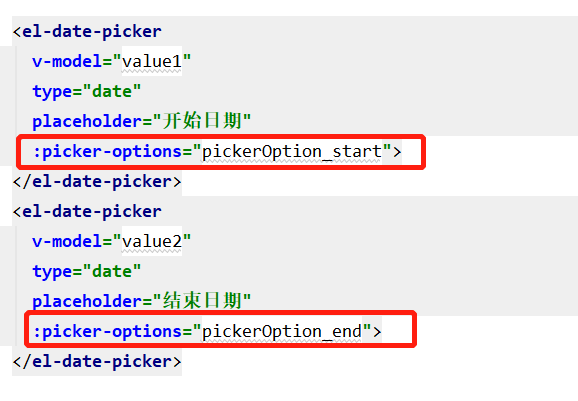
elementui 中 el-date-picker 控制选择当前年之前或者之后的年份
文章目录 需求分析 需求 对 el-date-picker控件做出判断控制 分析 给 el-date-picker 组件添加 picker-options 属性,并绑定对应数据 pickerOptions html <el-form-item label"雨量年份:" prop"date"><el-date-picker …...

GlusterFS:开源分布式文件系统的深度解析与应用场景实践
引言 在当今大数据时代背景下,企业对存储系统的容量、性能和可靠性提出了前所未有的挑战。GlusterFS作为一款开源的、高度可扩展的分布式文件系统,以其独特的无中心元数据设计和灵活的卷管理机制,在众多场景中脱颖而出,为解决大规…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
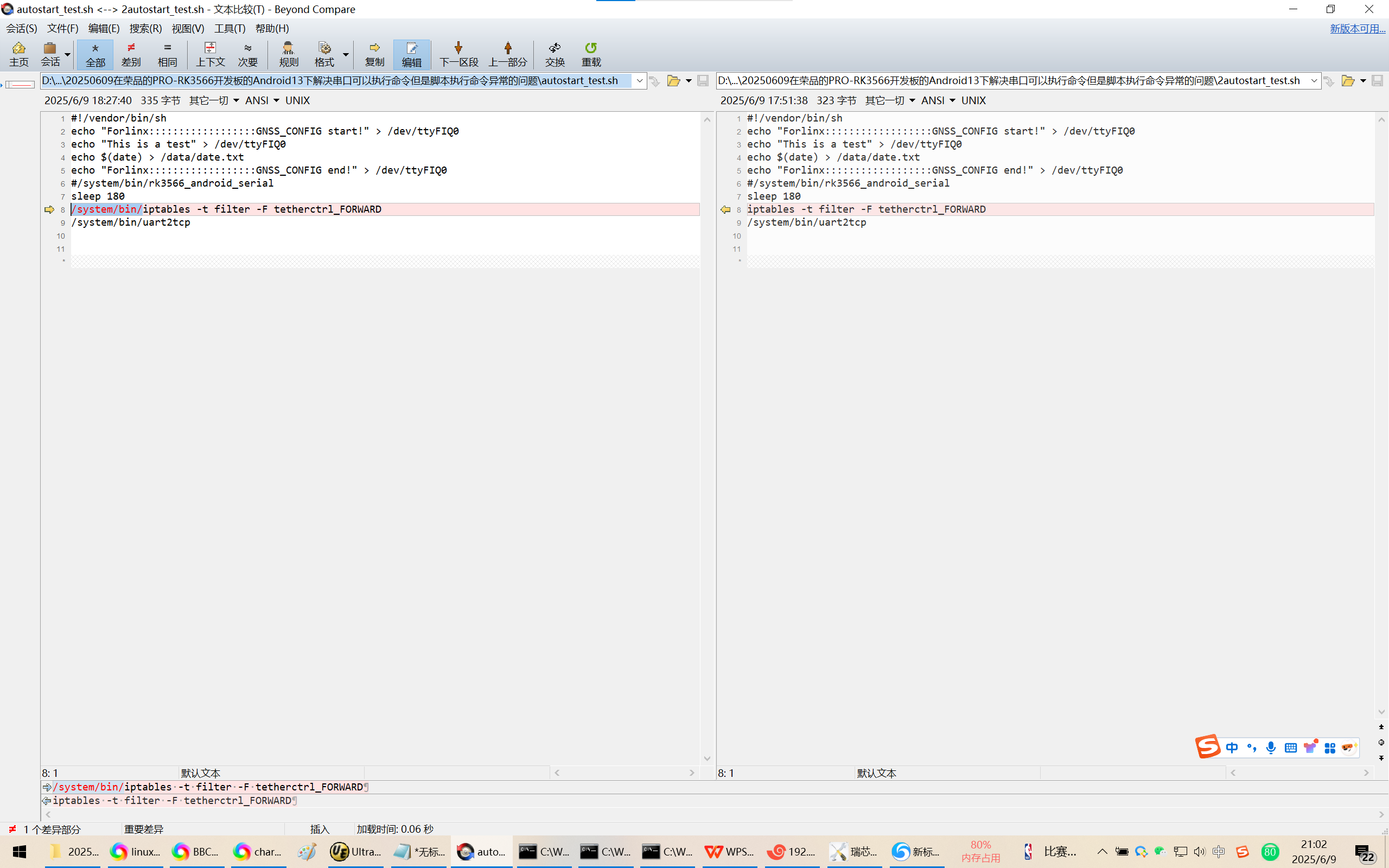
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...

Redis专题-实战篇一-基于Session和Redis实现登录业务
GitHub项目地址:https://github.com/whltaoin/redisLearningProject_hm-dianping 基于Session实现登录业务功能提交版本码:e34399f 基于Redis实现登录业务提交版本码:60bf740 一、导入黑马点评后端项目 项目架构图 1. 前期阶段2. 后续阶段导…...
