蓝桥杯备赛_python_BFS搜索算法_刷题学习笔记
1 bfs广度优先搜索
1.1 是什么
1.2怎么实现
2案例学习
2.1.走迷宫
2.2.P1443 马的遍历
2.3. 九宫重排(看答案学的,实在写不来)
2.4.青蛙跳杯子(学完九宫重排再做bingo)
2.5. 长草
3.总结
1 bfs广度优先搜索
【Python搜索算法】广度优先搜索(BFS)算法原理详解与应用,示例+代码_广度优先算法的路径搜索代码-CSDN博客
1.1 是什么
看了其他大佬的分享之后,我理解的广度优先搜索是一种图遍历的算法,简单来说是他的访问规则是一层一层的访问,先访问距离节点近的数据,再逐层拓展访问远的数据。与广度优先搜索密切相关的数据类型叫做队列。队列我们可以理解为是日常生活中排队所形成的队形,先进先出是队列最大的特点。
1.2怎么实现
BFS算法的步骤如下:
- 初始化:选择一个起始节点,将其标记为已访问,并将其放入队列中(作为起始节点)。
- 进入循环:重复以下步骤,直到队列为空。 a. 从队列中取出一个节点。 b. 访问该节点。 c. 将所有未访问的相邻节点加入队列。 d. 标记已访问的节点,以避免重复访问。
- 结束循环:当队列为空时,表示已经遍历完整个图。
算法原理:
BFS的工作原理是通过队列数据结构来管理待访问的节点。它从起始节点开始,然后逐一访问该节点的相邻节点,并将它们加入队列。然后,它从队列中取出下一个节点进行访问,以此类推。这确保了节点按照它们的距离从起始节点逐层遍历,因此BFS可以用于查找最短路径。
BFS是一个宽度优先的搜索,它在查找最短路径等问题中非常有用。它不会陷入深度过深的路径,因为它会优先探索距离起始节点更近的节点。
总结:广度优先搜索一般来说都会有一个队列去存储节点,同时也会有一个数组去记录访问的状态。
2案例学习
2.1.走迷宫

输入:
5 5
1 0 1 1 0
1 1 0 1 1
0 1 0 1 1
1 1 1 1 1
1 0 0 0 1
1 1 5 5 输出:
8说明一下这道题的思路,这道题非常直观体现了BFS,并且是最基本的BFS。那代码的思路是怎么样的呢?我们来捋一下。
一开始所说的队列其实就是列表,只是用到了队列的特点,也就是说队列其实就是类似于列表,只是这个算法的思路用到了队列的特点,一开始我想得太复杂了,总以为队列是一个很高级的容器,其实简单理解就是列表。
那根据BFS的算法思路:
- 初始化:将迷宫的起点作为起始节点 queue=[(x1-1,y1-1,step)]
- 进入循环:循环终止的条件是什么,当列表为空就终止了 while queue: 怎么取出列表的第一个元素,这个时候就是队列的特点,先进先出,怎么体现在列表中,进去就是存入,出来就是删除 x,y,step=queue.pop(0) 这里页需要注意走迷宫有上下左右四个方向对应的就是坐标的变化,这也是我对子节点的一个理解
同时已经访问过的点也要做好标记
我当时还有一个特别想不懂的,哈哈哈哈哈哈,想起来感觉自己特别蠢哈哈哈哈哈。
怎么着,我想着每一个节点都有四个子节点,那意味着线路会不一样,怎么就知道那一个的step是最小的,结果我看到那个判断的出口就一下子大悟了,最短路径嘛,那早点满足出口条件的不就是最短路径嘛
n, m = map(int,input().split())
data = []
d = [[1,0],[-1,0],[0,1],[0,-1]]
for i in range(n):l = list(map(int,input().split()))data.append(l)
x1, y1, x2, y2 = map(int,input().split())
def bfs(x1,y1,step):queue=[(x1-1,y1-1,step)]while queue:x,y,step=queue.pop(0)if x==x2-1 and y==y2-1:return stepfor xx,yy in d:dx = x+xxdy = y+yyif 0<= dx <n and 0<= dy <m and data[dx][dy] :data[dx][dy]=0queue.append((dx,dy,step+1))return -1
print(bfs(x1,y1,0))2.2.P1443 马的遍历

做好久了但是还是没有完全通过,怎么办可以帮忙看看嘛
n, m, x, y= map(int,input().split())
d = [[-1,2],[-2,1],[-2,-1],[-1,-2],[1,2],[2,1],[2,-1],[1,-2]]
data = []
result = [[0 for _ in range(m)]for _ in range(n)]
for i in range(1,n+1):for j in range(1,m+1):data.append([i,j])
from collections import deque
def bfs(x,y,a,b,step,visit):queue = deque([(x,y,step)])while len(queue) != 0:x1, y1, step = queue.popleft()if x1 == a and y1 == b:return stepfor xx,yy in d:dx = x1+xxdy = y1+yyif dx < 1 or dx > n or dy < 1 or dy > m:continueif visit[dx][dy] == 0:visit[dx][dy] = 1queue.append((dx, dy, step + 1))return -1for i,j in data:visit = [[0 for _ in range(m + 1)] for _ in range(n + 1)]visit[x][y] = 1ans = bfs(x,y,i,j,0,visit)result[i-1][j-1] = ans
for i in result:for j in i:print(j,end='\t')print('\n',end='')
2.3. 九宫重排(看答案学的,实在写不来)
6.九宫重排 - 蓝桥云课 (lanqiao.cn)
我当时自己做的时候就在纠结到底是移动格子还是移动数字,很显然,如果要移动数字那每个数字都需要移动,但是移动格子的话我们只需要对这个格子进行操作就可以了。所以移动格子是最佳方案。
以下是我自己写的错误代码,真的是错的离谱,纪念一下我稀里糊涂的脑子
start = input()
end = input()map1 = [[0 for _ in range(3)] for _ in range(3)]
map2 = [[0 for _ in range(3)] for _ in range(3)]
k1, k2 = 0, 0
for i in range(3):for j in range(3):map1[i][j] = start[k1]if start[k1] == '.':a, b = i, jk1 += 1
for i in range(3):for j in range(3):map2[i][j] = end[k2]k2 += 1d = [[1,0],[-1,0],[0,1],[0,-1]]def bfs(a,b,step):global map1visit = [[0 for _ in range(3)] for _ in range(3)]queue = [(a,b,step)]visit[a][b] = 1while queue:x, y, step = queue.pop(0)if map1 == map2:return stepfor xx,yy in d:dx = x+xxdy = y+yyif dx<0 or dx>2 or dy<0 or dy>2:continueif visit[dx][dy] == 0:visit[dx][dy] = 1map1[x][y],map1[dx][dy] = map1[dx][dy],map1[x][y]queue.append((dx,dy,step+1))return -1
print(bfs(a,b,0))
别人大佬的代码代码写的真好
蓝桥杯:九宫格重排【BFS】【Python】_重排九宫问题bfs-CSDN博客
当然我在别人的代码上加上了一些修改以及注释,主要是得自己看得懂
我也反思了一下自己写的代码思路和别人的,我在一维和二维的变换上处理的十分混乱,导致自己都不知道到底是个什么事儿,因为我也知道是去移动格子,然后交换,但是我就很混乱。当然我的思路还有一些错误。
别人的代码思路这一点我真是没想到,就是用字典的键值对去存储每一次移动格子后所形成的新字符串的步数,一旦相等了就可以直接返回。
start = input()
end = input()from collections import deque
def bfs():# 创建容器并初始化# 创建字典存储每次变换字符串的步数dic = {}dic[start] = 0# 创建队列queue = deque()queue.append(start)d = [[1, 0], [-1, 0], [0, 1], [0, -1]]# 进入循环while queue:now_start = list(queue.popleft())# 循环结束出口if "".join(now_start) == end:return dic["".join(now_start)]point = now_start.index('.')# 一维的下标转换为二维下标:# 转换公式:x = index//二维数组的宽度 y = index%二维数组的宽度x = point // 3y = point % 3step = dic["".join(now_start)]for xx,yy in d:dx = x+xxdy = y+yyif dx>=0 and dx<3 and dy>=0 and dy<3:new_start = now_start.copy()# 二维转一维# 转换公式:index = x*二维数组的宽度 + ynew_start[point],new_start[dx*3+dy] = new_start[dx*3+dy],new_start[point]if "".join(new_start) not in dic.keys():# dic.setdefault("".join(new_start),step+1)dic["".join(new_start)] = step+1queue.append("".join(new_start))return -1print(bfs())
知识点笔记:
2.4.青蛙跳杯子(学完九宫重排再做bingo)
1.青蛙跳杯子 - 蓝桥云课 (lanqiao.cn)
那学完九宫重排之后写这道题就非常简单了,并且这道题还是一维的,不用转换,其他思路跟九宫重排一模一样。
题目中所说的三种动作,虽然说是青蛙的跳动,但是把当作杯子的跳动去处理就会简单很多,总之学完九宫重排之后这道题就是很简单了。
start = input()
end = input()from collections import deque
def bfs():d = [1, -1, 2, -2, 3, -3]queue = deque()queue.append(start)dic = {}dic[start] = 0while queue:now_start = list(queue.popleft())point = now_start.index('*')step = dic["".join(now_start)]if "".join(now_start) == end:return dic["".join(now_start)]for xx in d:dx = point+xxnew_start = now_start.copy()if dx in range(0, len(start)):new_start[point], new_start[dx] = new_start[dx], new_start[point]if "".join(new_start) not in dic.keys():dic["".join(new_start)] = step+1queue.append("".join(new_start))return -1print(bfs())
2.5. 长草
0长草 - 蓝桥云课 (lanqiao.cn)
这道题一开始的思路是想到了非连通图的遍历,然后我就是这么一个思路,先找到一个初始化的点先进行广度优先搜索,只进行K层的搜索,但是我一直都无法找到怎样去把握让搜索测层数是我想要的,不知道这个怎么解决,在这里遇到了大问题,然后再遍历我的地图看看还有没有另外的点需要搜索的。所以这个思路就需要两个数组,一个是队列,一个是记录我的访问状态,但是我并没有解决。
然后就换了一个思路,将节点先依次入队,再对每一个节点进行广度优先搜索,这个就比较好控制,多少层那我就调用多少次的bfs。这里有一个点就在于我的while循环的出口是与队列的长度有关(或者是说节点的个数),因为队列只有把所有的节点都遍历完成之后才算。
总之这道题也是一道与之前有着一点区别的,也可以算作是遍历非连通图的一种方法。
n, m = map(int,input().split())
maps = []
for i in range(n):l = list(input())maps.append(l)
k = int(input())from collections import deque
queue = deque()
for i in range(n):for j in range(m):if maps[i][j] == 'g':queue.append((i,j))d = [[1,0],[-1,0],[0,1],[0,-1]]
def bfs():ans = len(queue)while ans:x1, y1 = queue.popleft()for xx,yy in d:dx = x1+xxdy = y1+yy# if dx<0 or dx>=n or dy<0 or dy>=m:# continuif 0<=dx<n and 0<=dy<m and maps[dx][dy] == '.':maps[dx][dy] = 'g'queue.append((dx,dy))ans -= 1for i in range(k):bfs()
for i in maps:print(''.join(i)) 
3.总结
学习还在继续,持续学习加油!!!!
相关文章:

蓝桥杯备赛_python_BFS搜索算法_刷题学习笔记
1 bfs广度优先搜索 1.1 是什么 1.2怎么实现 2案例学习 2.1.走迷宫 2.2.P1443 马的遍历 2.3. 九宫重排(看答案学的,实在写不来) 2.4.青蛙跳杯子(学完九宫重排再做bingo) 2.5. 长草 3.总结 1 bfs广度优先搜索 【P…...
)
轮播图的五种写法(原生、vue2、vue3、react类组件,react函数组件)
轮播图效果是一种在网页或应用程序中展示多张图片或内容的方式,通常以水平或垂直的方式循环播放。本文使用原生、vue2、vue3、react类组件,react函数组件五种写法实现了简单的轮播图效果,需要更多轮播效果需要再增加样式或者动画。 淡入淡出效果:每张图片渐渐淡入显示,然后…...
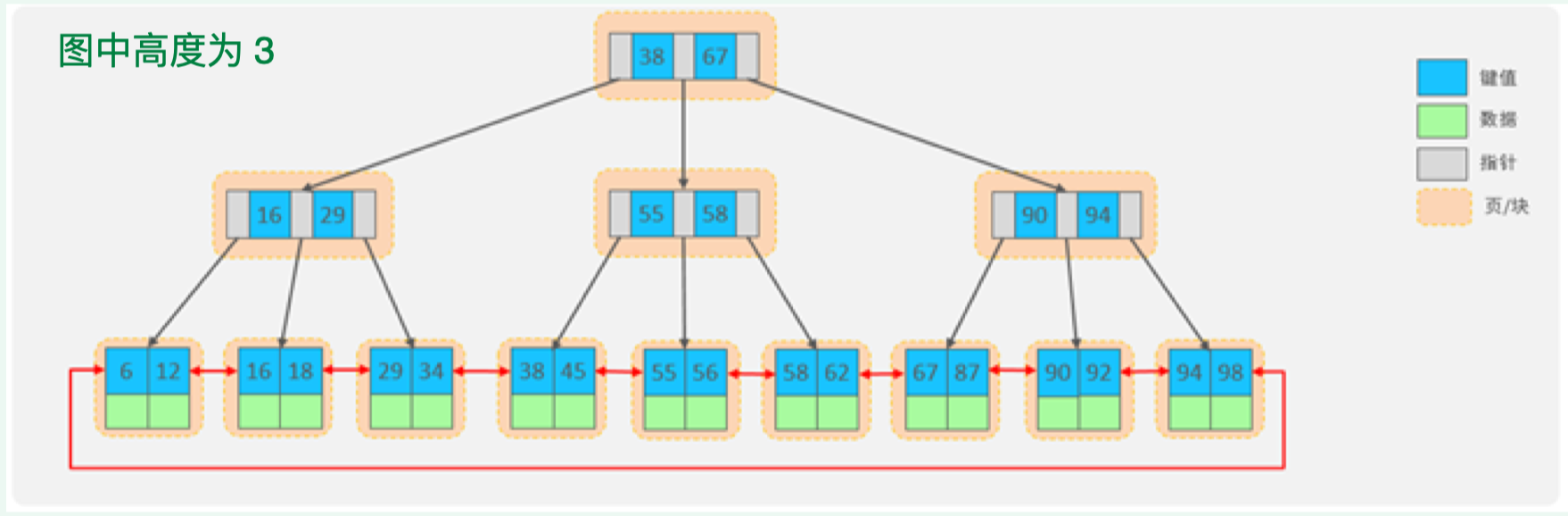
【MySQL】高度为2和3时B+树能够存储的记录数量的计算过程
文章目录 题目答案高度为2时的B树高度为3时的B树总结 GPT4 对话过程 题目 InnoDB主键索引的Btree在高度分别为 2 和 3 时,可以存储多少条记录? 答案 高度为2时的B树 计算过程: 使用公式 ( n 8 ( n 1 ) 6 16 1024 ) (n \times 8 …...
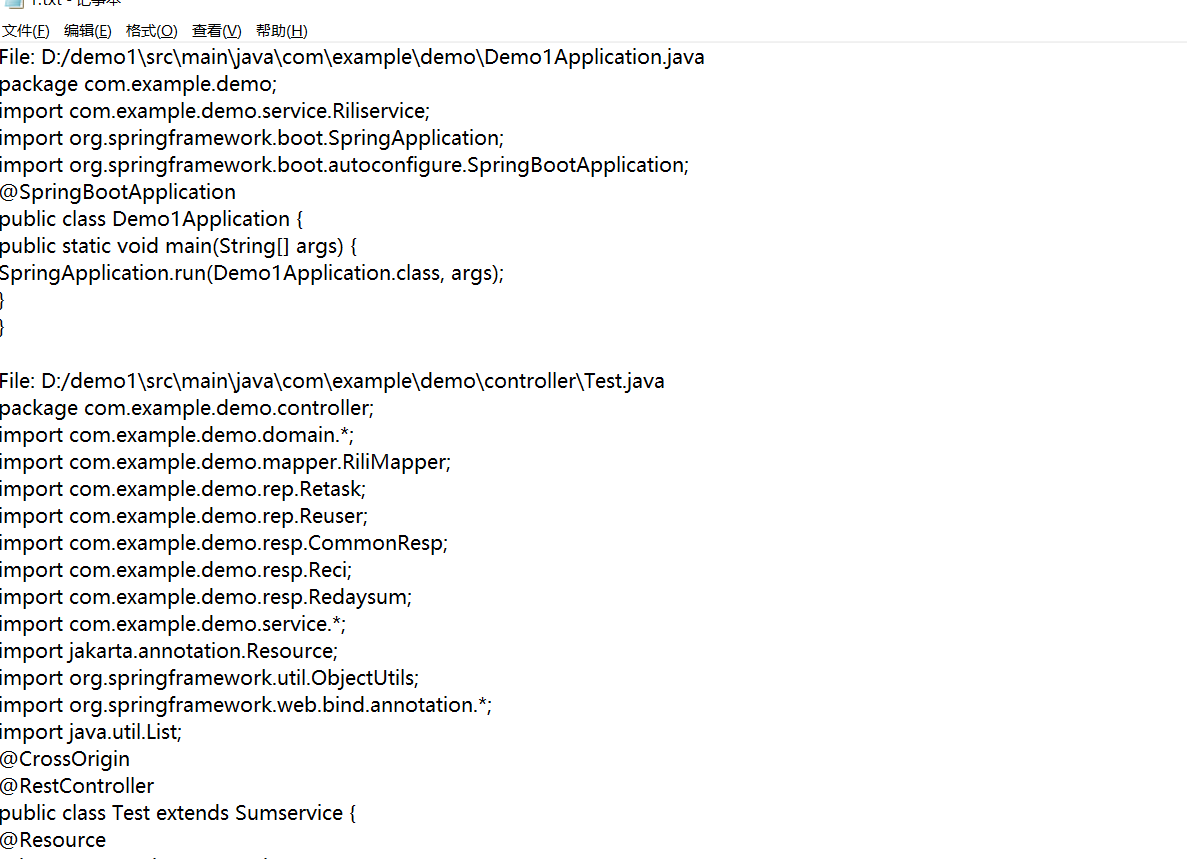
软件著作书 60页代码轻松搞定!(附exe和代码)
最近做了一个软件,准备去申请软件著作书,看着那60页的文档,确实难搞,不过幸好会用一点点python,就自己用python写了一个读取所有文件代码的程序,使用起来也很简单,过来分享一下 链接࿱…...

阿里文档类图像的智能识别,文档分类自定义分类器
阿里云文档类图像智能识别服务为用户提供了强大的文档处理能力,可以将文档图像中的文本内容、表格数据和结构化信息自动识别并提取出来。而自定义分类器则允许用户根据自己的需求,训练出更适合自己场景的文档分类模型。本文将详细介绍阿里云文档类图像智…...
)
256.【华为OD机试真题】会议室占用时间(区间合并算法-JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目二.解题思路三.题解代码Python题解代码JAVA题解…...
人工智能学习与实训笔记(三):神经网络之目标检测问题
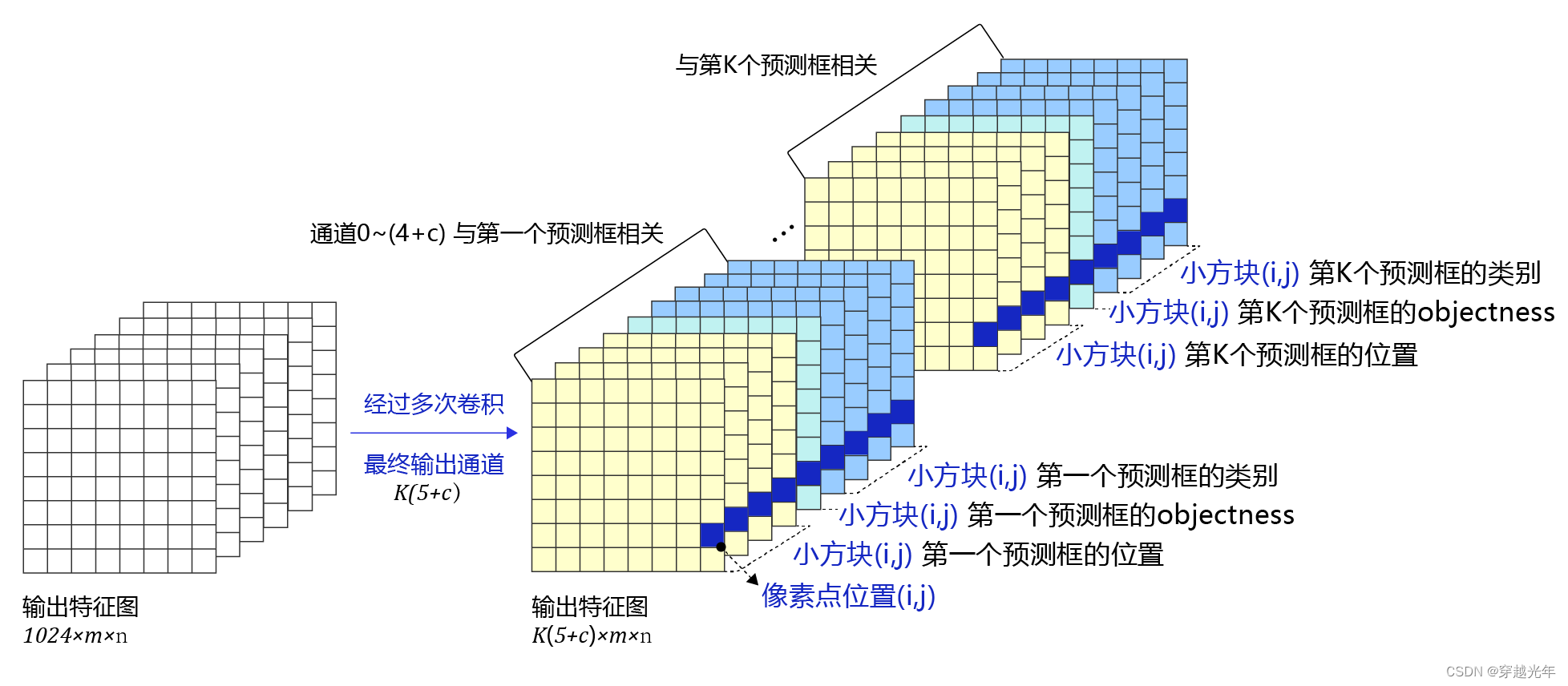
人工智能专栏文章汇总:人工智能学习专栏文章汇总-CSDN博客 目录 三、目标检测问题 3.1 目标检测基础概念 3.1.1 边界框(bounding box) 3.1.2 锚框(Anchor box) 3.1.3 交并比 3.2 单阶段目标检测模型YOLOv3 3.2…...
)
SSM框架,Spring-ioc的学习(下)
拓展:在xml文件中读取外部配置文件 例:若要导入外部配置文件jdbc.properties <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"<http://www.springframework.org/schema/beans>"xmlns:xsi"&l…...

【AIGC】Stable Diffusion的模型微调
为什么要做模型微调 模型微调可以在现有模型的基础上,让AI懂得如何更精确生成/生成特定的风格、概念、角色、姿势、对象。Stable Diffusion 模型的微调方法通常依赖于您要微调的具体任务和数据。 下面是一个通用的微调过程的概述: 准备数据集…...
VNCTF 2024 Web方向 WP
Checkin 题目描述:Welcome to VNCTF 2024~ long time no see. 开题,是前端小游戏 源码里面发现一个16进制编码字符串 解码后是flag CutePath 题目描述:源自一次现实渗透 开题 当前页面没啥好看的,先爆破密码登录试试。爆破无果…...
第11章 GUI
11.1 Swing概述 Swing是Java语言开发图形化界面的一个工具包。它以抽象窗口工具包(AWT)为基础,使跨平台应用程序可以使用可插拔的外观风格。Swing拥有丰富的库和组件,使用非常灵活,开发人员只用很少的代码就可以创建出…...
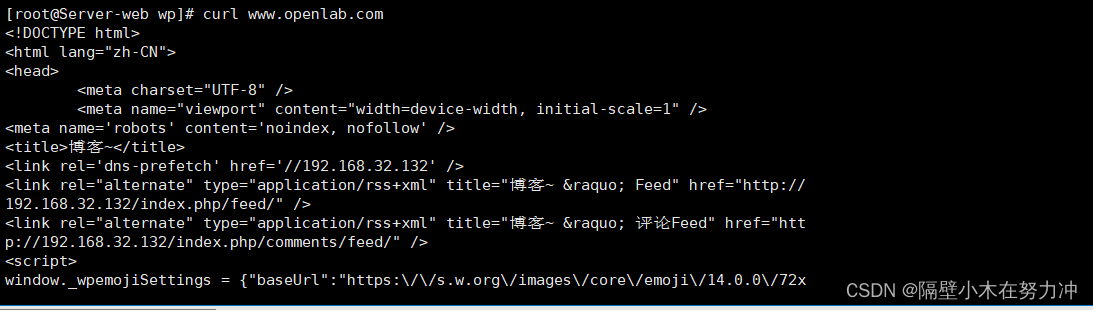
综合项目---博客
一.运行环境 192.168.32.132 Server-Web linux Web 192.168.32.133 Server-NFS-DNS linux NFS/DNS 基础配置 1.配置主机名静态ip 2.开启防火墙并配置 3.部分开启selinux并配置 4.服务器之间通过阿里云进行时间同步 5.服务器之间实现ssh免密…...

leetcode(矩阵)74. 搜索二维矩阵(C++详细解释)DAY7
文章目录 1.题目示例提示 2.解答思路3.实现代码结果 4.总结 1.题目 给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非严格递增顺序排列。每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中…...
超详细||YOLOv8基础教程(环境搭建,训练,测试,部署看一篇就够)(在推理视频中添加FPS信息)
一、YOLOv8环境搭建 这篇文章将跳过基础的深度学习环境的搭建,如果没有完成的可以看我的这篇博客:超详细||深度学习环境搭建记录cudaanacondapytorchpycharm-CSDN博客 1. 在github上下载源码: GitHub - ultralytics/ultralytics: NEW - YO…...

LeetCode171. Excel Sheet Column Number
文章目录 一、题目二、题解 一、题目 Given a string columnTitle that represents the column title as appears in an Excel sheet, return its corresponding column number. For example: A -> 1 B -> 2 C -> 3 … Z -> 26 AA -> 27 AB -> 28 … Exa…...
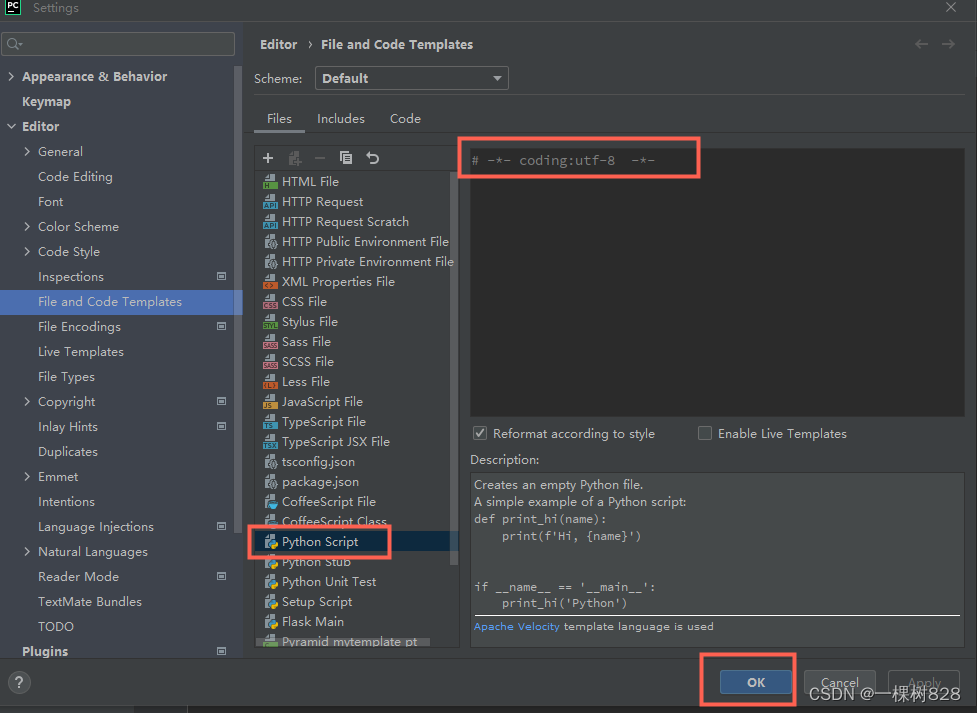
pycharm创建py文件,自动带# -*- coding:utf-8 -*-
File–Settings...
希捷与索尼集团合作生产HAMR写头激光二极管
最近有报道指出,希捷(Seagate)在生产其采用热辅助磁记录(HAMR)技术的大容量硬盘时,并非所有组件都在内部制造。根据日经新闻的一份新报告,希捷已与索尼集团合作,由索尼为其HAMR写头生…...
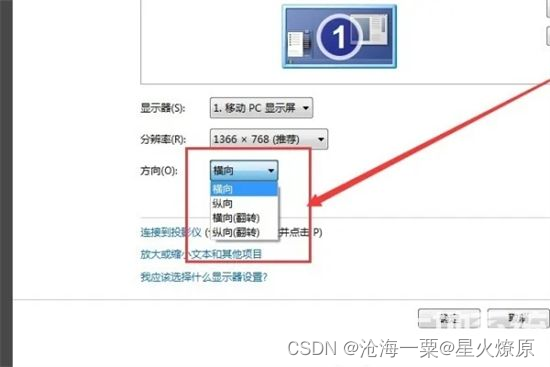
电脑竖屏显示了怎么回复原状
电脑屏幕变成这样 怎么恢复原状? 1、登录系统 2、在桌面上空白点击鼠标右键 3、在右键菜单中选择“屏幕分辨率”,左键点击打开 4、在窗口中“方向”位置选择“横向” 5、保存设置win7桌面即可恢复到正常状态...

Elasticsearch从入门到精通
目录 🧂1.简单介绍 🥓2.安装与下载 🌭3.安装启动es 🍿4.安装启动kibana 🥞5.初步检索 🧈6.进阶检索 🫓7.Elasticsearch整合 1.简单介绍🚗🚗🚗 Elat…...
Halcon 相机标定
文章目录 算子单相机标定单相机标定畸变的矫正 算子 gen_caltab 生成标定文件 gen_caltab(::XNum,YNum,MarkDist,DiameterRatio,CalTabDescrFile,CalTabPSFile :) 算子来制作一个标定板XNum 每行黑色标志圆点的数量。YNum 每列黑色标志圆点的数…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...



