[蓝桥 2017]九宫幻方
九宫幻方
题目描述
小明最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分,三阶幻方指的是将 1~9 不重复的填入一个 3*3 的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。
三阶幻方又被称作九宫格,在小学奥数里有一句非常有名的口诀:"二四为肩,六八为足,左三右七,戴九履一,五居其中",通过这样的一句口诀就能够非常完美的构造出一个九宫格来。
4 9 2
3 5 7
8 1 6
有意思的是,所有的三阶幻方,都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。现在小明准备将一个三阶幻方(不一定是上图中的那个)中的一些数抹掉,交给邻居家的小朋友来进行还原,并且希望她能够判断出究竟是不是只有一个解。
而你呢,也被小明交付了同样的任务,但是不同的是,你需要写一个程序。
输入描述
输入仅包含单组测试数据。
每组测试数据为一个 3*3 的矩阵,其中为 0 的部分表示被小明抹去的部分。
给出的矩阵至少能还原出一组可行的三阶幻方。
输出描述
如果仅能还原出一组可行的三阶幻方,则将其输出,否则输出"Too Many"(不包含引号)。
输入输出样例
示例
输入
0 7 2
0 5 0
0 3 0
输出
6 7 2
1 5 9
8 3 4
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
总通过次数: 1096 | 总提交次数: 1260 | 通过率: 87%
难度: 困难 标签: 2017, 暴力, 省赛, 搜索
代码分享:
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int p[10],a[5][5],b[5][5],ans[5][5];
int main()
{for(int i=1;i<=3;i++)for(int j=1;j<=3;j++)cin>>a[i][j];//读入样例矩阵for(int i=1;i<=9;i++)p[i]=i;int cnt=0;//统计九宫幻方的个数do{b[1][1]=p[1],b[1][2]=p[2],b[1][3]=p[3];b[2][1]=p[4],b[2][2]=p[5],b[2][3]=p[6];b[3][1]=p[7],b[3][2]=p[8],b[3][3]=p[9];//判断排列矩阵和样例矩阵是否匹配bool flag = true;//flag = ture表示匹配,flag = false表示不匹配for(int i=1;i<=3;i++){for(int j=1;j<=3;j++){if(!a[i][j]) continue;//只看非零部分if(a[i][j] != b[i][j]) flag = false;}}if(!flag) continue;//如果不匹配//判断排列矩阵是否是九宫幻方bool ok = true;//ok = ture表示排列矩阵是九宫幻方,ok = flase表示排列矩阵不是九宫幻方int sum = b[1][1] + b[2][2] + b[3][3];//取一条对角线if(sum !=b[1][3]+b[2][2]+b[3][1]) continue;//判断另一条对角线的和是否等于sum,不等于就跳过for(int i=1;i<=3;i++){int tmp1 = 0,tmp2 = 0;//tmp1表示行和,temp2表示列和for(int j=1;j<=3;j++){tmp1+=b[i][j];tmp2+=b[j][i];}if(tmp1 !=sum ||tmp2 !=sum)ok =false;//如果行的和或列的和不等于sum,则排列矩阵不是九宫幻方}if(!ok) continue;//如果不是九宫幻方,就跳过cnt++;//九宫幻方的个数+1if(cnt>=2)return cout<<"Too Many\n",0;//九宫幻方的个数》=2,直接输出Too Many,结束程序for(int i = 1;i<=3;i++)for(int j = 1;j <= 3;j++)ans[i][j] = b[i][j];//用ans记录下该九宫幻方}while(next_permutation(p + 1,p + 1 + 9));for(int i=1;i<=3;i++){for(int j=1;j<=3;j++){if(j==1)cout<<ans[i][j];elsecout<<" "<<ans[i][j];}cout<<endl;}// 请在此输入您的代码return 0;
}相关文章:

[蓝桥 2017]九宫幻方
九宫幻方 题目描述 小明最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分,三阶幻方指的是将 1~9 不重复的填入一个 3*3 的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。 三阶幻方又被称作九宫格…...
”的解决方法)
Qt - 编译报错:“invalid use of incomplete type ‘class Ui::xxx‘ui(new Ui::xxx)”的解决方法
问题起因 今天在创建Qt设计器界面类时,类名的英文拼写错误,然后就重命名了文件,而Qt Creator也帮我自动修改了一部分内容,之后我手动将cpp文件中的#include " *** "里的内容给修改了,构造函数和析构函数处也…...
基于Doris构建亿级数据实时数据分析系统
背景 随着公司业务快速发展,对业务数据进行增长分析的需求越来越迫切,与此同时我们的业务数据量也在快速激增、每天的数据新增量大概在30w 左右,一年就会产生1 个亿的数据,显然基于传统MySQL数据库已经无法支撑满足以上需求 基于上…...

javascript中的prototype;javascript中的原型链
文章目录 深入理解JavaScript原型链1. 什么是原型链?2. 原型链的结构3. 如何访问原型链?4. 示例演示原型链5. 原型链与继承6. 实际应用场景 深入理解JavaScript原型链 1. 什么是原型链? 在JavaScript中,每个对象都有一个原型&am…...
CI/CD部署
什么是CI,什么是CD CI和CD是软件开发中持续集成和持续交付的缩写。 CI代表持续集成(Continuous Integration),是一种实践,旨在通过自动化构建、测试和代码静态分析等过程,频繁地将代码变更合并到共享存储…...

定点数,定点数二维向量,定点数三维向量,定点数数学类
定点数,定点数二维向量,定点数三维向量,定点数数学类 介绍浮点数定点数封装的定点数FixedNumber定点数二维向量定点数三维向量定点数数学类总结 介绍 众所周知定点数是用于做帧同步时保持不同cpu不同设备保持一致稳定的代替浮点数的变量&…...
安装ts-node有感
起因:想要在vsCode上运行ts脚本 解决方案: 1.安装vsCode插件 code runner 2.全局安装ts-node 这一步遇到三个问题: ①.node版本问题:需安装版本18以上node,可使用nvm去控制不同的node版本 ②.certificate has exp…...

飞天使-k8s知识点18-kubernetes实操3-pod的生命周期
文章目录 探针的生命周期流程图prestop 探针的生命周期 docker 创建:在创建阶段,你需要选择一个镜像来运行你的应用。这个镜像可以是公开的,如 Docker Hub 上的镜像,也可以是你自己创建的自定义镜像。创建自己的镜像通常需要编写一…...

顺子日期 蓝桥杯
调用API 思路: 设置Calendar的属性,获取Calendar的毫秒数,转换成指定格式的字符串(yyyyMMdd),判断字符串中是否包含符合条件的,若有就1, 迭代: 每次循环给Calendar加上一天即可 import java.text.SimpleDateFormat; im…...
基于 Python 的景区票务人脸识别系统,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

OpenAI全新发布的Sora,到底意味着什么?
16日凌晨,OpenAI发布了文本视频的工具(text-do-video)Sora,整个世界再次被震撼。 Sora的出现,到底意味着什么? 目录 Sora的背景与概述Sora是什么?能为我们做些什么?存在的一些问题 文…...

预防.locked.locked1勒索病毒攻击:保护数据安全
导言: 随着科技的发展,网络安全问题日益严重,其中勒索病毒是一种令人头痛的威胁。.locked和.locked1是两种常见的勒索病毒,它们会将用户的数据文件加密,并要求支付赎金以获取解密密钥。本文将介绍这两种勒索病毒的特点…...
【力扣hot100】刷题笔记Day5
前言 回学校了,荒废了半天之后打算奋发图强猛猛刷题,找实习!赚钱!! 560. 和为 K 的子数组 - 力扣(LeetCode) 前缀法 哈希表 这个题解解释比官方清晰,截个图方便看,另一…...

解锁Spring Boot中的设计模式—04.桥接模式:探索【桥接模式】的奥秘与应用实践!
桥接模式 桥接模式也称为桥梁模式、接口模式或者柄体(Handle and Body)模式,是将抽象部分与他的具体实现部分分离,使它们都可以独立地变化,通过组合的方式建立两个类之间的联系,而不是继承。 桥接模式是一种…...

[talib][python]ta-lib所有whl文件下载地址汇总
TA-Lib-0.4.28-cp312-cp312-win-amd64.whl下载地址:https://download.csdn.net/download/FL1623863129/88589956 ta-lib-0.4.25-cp311-cp311-win-amd64.whl下载地址:https://download.csdn.net/download/FL1623863129/88265329 TA-Lib-0.4.24-cp310-cp31…...

【开源】JAVA+Vue.js实现农村物流配送系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统登录、注册界面2.2 系统功能2.2.1 快递信息管理:2.2.2 位置信息管理:2.2.3 配送人员分配:2.2.4 路线规划:2.2.5 个人中心:2.2.6 退换快递处理:…...

锁相放大器,数字锁相放大器.C和python版的源代码
数字锁相放大器. 锁相放大器, 它是一种可以从高噪声环境中提取出特定频率信号的放大器,工作原理主要是利用正弦函数的正交性进行信号的相位检测和幅值测量。如果你对锁相放大器感兴趣,我可以给你更详细的解释。 数字锁相放大器是利用软件算法来实现提取…...
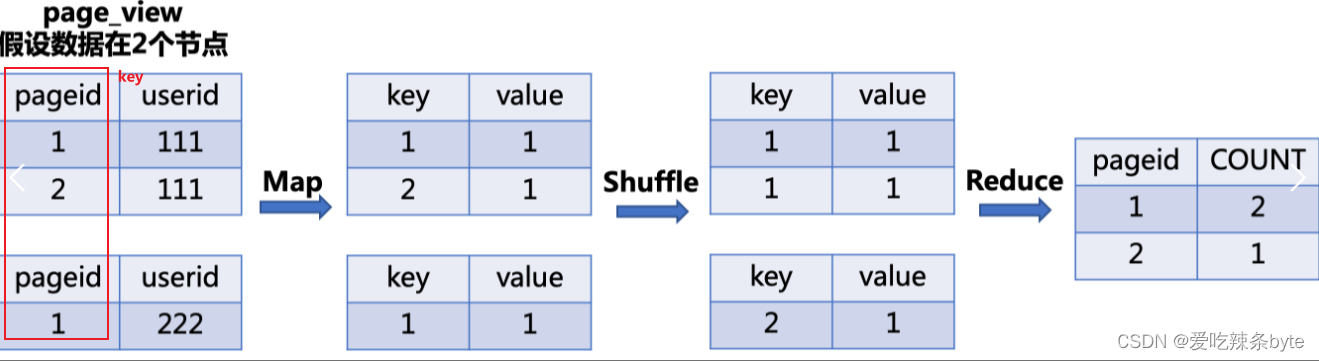
(02)Hive SQL编译成MapReduce任务的过程
目录 一、架构及组件介绍 1.1 Hive底层架构 1.2 Hive组件 1.3 Hive与Hadoop交互过程 二、Hive SQL 编译成MR任务的流程 2.1 HQL转换为MR源码整体流程介绍 2.2 程序入口—CliDriver 2.3 HQL编译成MR任务的详细过程—Driver 2.3.1 将HQL语句转换成AST抽象语法树 词法、语…...

【C++初阶】值得一刷的字符串string相关oj题
👦个人主页:Weraphael ✍🏻作者简介:目前学习C和算法 ✈️专栏:C航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞…...

《Go 简易速速上手小册》第10章:微服务与云原生应用(2024 最新版)
文章目录 10.1 构建微服务架构 - 探索 Go 语言的微观世界10.1.1 基础知识讲解10.1.2 重点案例:订单处理系统订单服务测试服务 10.1.3 拓展案例 1:用户认证服务安装所需的包实现用户模型和存储实现 JWT 生成和验证实现认证服务测试服务 10.1.4 拓展案例 2…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
