P3141 [USACO16FEB] Fenced In P题解
题目
如果此题数据要小一点,那么我们可以用克鲁斯卡尔算法通过,但是这个数据太大了,空间会爆炸,时间也会爆炸。
我们发现,如果用 MST 做,那么很多边的边权都一样,我们可以整行整列地删除。
我们造一个样例解析一下:
+-+--+---+
| | | |
+-+--+---+
| | | |
| | | |
+-+--+---+
首先,我们删除第一列的栅栏:
+-+--+---+
| | | |
+ +--+---+
| | | |
| | | |
+-+--+---+
此时答案是 1 1 1。
再删除第一排的栅栏:
+-+--+---+
| |
+ +--+---+
| | | |
| | | |
+-+--+---+
此时答案是 3 3 3。
我们继续删除第二列的栅栏:
+-+--+---+
| |
+ + +---+
| | | |
| | | |
+-+--+---+
此时答案是 5 5 5。
我们继续删除第二行的栅栏:
+-+--+---+
| |
+ + +---+
| |
| |
+-+--+---+
此时答案是 9 9 9。
我们把第三列的栅栏删除,由于之前删除的两行栅栏导致第三列栅栏少删除一个,不用删除。
你可以继续造更大的数据发现规律:
我们先把每一列,每一行的栅栏长度算出来,从小到达排序,然后用双指针算法,两个指针 i i i 和 j j j,第一个记录统计到哪一行,第二个记录统计到哪一列,这两个变量的初始值应该为 2 2 2,然后把第一列,第一行栅栏删除。讨论时,如果我们当前讨论的行比列要短,就删除 m − j + 1 m-j+1 m−j+1 个栅栏,因为之前删除的栅栏导致我们现在不用删除一些栅栏。反之,同理,就是 n − i + 1 n-i+1 n−i+1 个栅栏。如果一个指针走完了,那么所有的都是联通的,就不用再循环了。时间复杂度 O ( n ) O(n) O(n),通过。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
int h, w, n, m;
int a[300000], b[300000];
long long a1[300000], b1[300000];
long long ans;int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> h >> w >> n >> m;for (int i = 1; i <= n; i ++) cin >> a[i];for (int i = 1; i <= m; i ++) cin >> b[i];sort(a + 1, a + n + 1);sort(b + 1, b + m + 1);n++;a[n] = h;m++;b[m] = w;for (int i = 1; i <= n; i ++) {a1[i] = a[i] - a[i - 1];}for (int i = 1; i <= m; i ++) {b1[i] = b[i] - b[i - 1];}sort(a1 + 1, a1 + n + 1);sort(b1 + 1, b1 + m + 1);
// for (int i = 1; i <= n; i ++) {
// cout << a1[i] << ' ';
// }
// cout << '\n';
// for (int j = 1; j <= m; j ++) {
// cout << b1[j] << ' ';
// }
// cout << '\n';int i = 2, j = 2;ans = a1[1] * (m - 1);ans += b1[1] * (n - 1);while (i <= n && j <= m) {if (a1[i] < b1[j]) {ans += a1[i] * (m - j + 1);i++;}else {ans += b1[j] * (n - i + 1);j++;}}cout << ans;return 0;
}
相关文章:

P3141 [USACO16FEB] Fenced In P题解
题目 如果此题数据要小一点,那么我们可以用克鲁斯卡尔算法通过,但是这个数据太大了,空间会爆炸,时间也会爆炸。 我们发现,如果用 MST 做,那么很多边的边权都一样,我们可以整行整列地删除。 我…...

Android Compose 一个音视频APP——Magic Music Player
Magic Music APP Magic Music APP Magic Music APP概述效果预览-视频资源功能预览Library歌曲播放效果预览歌曲播放依赖注入设置播放源播放进度上一首&下一首UI响应 歌词歌词解析解析成行逐行解析 视频播放AndroidView引入Exoplayer自定义Exoplayer样式横竖屏切换 歌曲多任…...

Nginx实战:安装搭建
目录 前言 一、yum安装 二、编译安装 1.下载安装包 2.解压 3.生成makefile文件 4.编译 5.安装执行 6.执行命令软连接 7.Nginx命令 前言 nginx的安装有两种方式: 1、yum安装:安装快速,但是无法在安装的时候带上想要的第三方包 2、…...
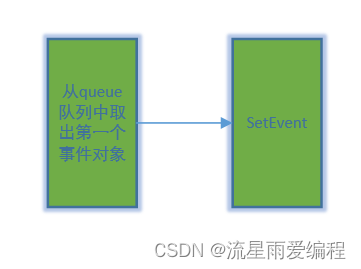
Qt之条件变量QWaitCondition详解(从使用到原理分析全)
QWaitCondition内部实现结构图: 相关系列文章 C之Pimpl惯用法 目录 1.简介 2.示例 2.1.全局配置 2.2.生产者Producer 2.3.消费者Consumer 2.4.测试例子 3.原理分析 3.1.源码介绍 3.2.辅助函数CreateEvent 3.3.辅助函数WaitForSingleObject 3.4.QWaitCo…...

OpenSource - 一站式自动化运维及自动化部署平台
文章目录 orion-ops 是什么重构特性快速开始技术栈功能预览添砖加瓦License orion-ops 是什么 orion-ops 一站式自动化运维及自动化部署平台, 使用多环境的概念, 提供了机器管理、机器监控报警、Web终端、WebSftp、机器批量执行、机器批量上传、在线查看日志、定时调度任务、应…...
【后端高频面试题--设计模式下篇】
🚀 作者 :“码上有前” 🚀 文章简介 :后端高频面试题 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 后端高频面试题--设计模式下篇 往期精彩内容设计模式总览模板方法模式怎么理解模板方法模式模板方…...
这才是大学生该做的副业,别再痴迷于游戏了!
感谢大家一直以来的支持和关注,尤其是在我的上一个公众号被关闭后,仍然选择跟随我的老粉丝们,你们的支持是我继续前行的动力。为了回馈大家长期以来的陪伴,我决定分享一些实用的干货,这些都是我亲身实践并且取得成功的…...
Ubuntu20.04 安装jekyll
首先使根据官方文档安装:Jekyll on Ubuntu | Jekyll • Simple, blog-aware, static sites 如果没有报错,就不用再继续看下去了。 我这边在执行gem install jekyll bundler时报错,所以安装了rvm,安装rvm可以参考这篇文章Ubuntu …...

AWK语言
一. awk awk:报告生成器,格式化输出。 在 Linux/UNIX 系统中,awk 是一个功能强大的编辑工具,逐行读取输入文本,默认以空格或tab键作为分隔符作为分隔,并按模式或者条件执行编辑命令。而awk比较倾向于将一行…...

精通Nmap:网络扫描与安全的终极武器
一、引言 Nmap,即NetworkMapper,是一款开源的网络探测和安全审计工具。它能帮助您发现网络中的设备,并识别潜在的安全风险。在这个教程中,我们将一步步引导您如何有效地使用Nmap,让您的网络更加安全。 因为Nmap还有图…...

Java 学习和实践笔记(11)
三大神器: 官方网址: http://www.jetbrains.com/idea/ 官方网址: https://code.visualstudio.com/ 官方网址: http://www.eclipse.org 装好了idea社区版,并试运行以下代码,OK! //TIP To <b>Run</b> code, press &l…...

开发实体类
开发实体类之间先在pom文件中加入该依赖 <!-- 开发实体类--><dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><scope>provided</scope></dependency>我们在实体类中声明各个属…...

人工智能学习与实训笔记(十五):Scikit-learn库的基础与使用
人工智能专栏文章汇总:人工智能学习专栏文章汇总-CSDN博客 本篇目录 一、介绍 1. 1 Scikit-learn的发展历程及定义 1.2 理解算法包、算法库及算法框架之间的区别和联系 二、Scikit-learn官网结构 三、安装与设置 3.1 Python环境的安装与配置 3.2 Scikit-lea…...

插值与拟合算法介绍
在数据处理和科学计算领域,插值与拟合是两种极为重要的数据分析方法。它们被广泛应用于信号处理、图像处理、机器学习、金融分析等多个领域,对于理解和预测数据趋势具有至关重要的作用。本文将深入浅出地介绍这两种算法的基本原理,并结合C语言编程环境探讨如何在CSDN开发者社…...

下一代Windows系统曝光:基于GPT-4V,Agent跨应用调度,代号UFO
下一代Windows操作系统提前曝光了?? 微软首个为Windows而设的智能体(Agent) 亮相: 基于GPT-4V,一句话就可以在多个应用中无缝切换,完成复杂任务。整个过程无需人为干预,其执行成功…...

二.自定义头文件
一.Worker.h 1.1概述 - 类名:Worker - 继承关系:所有其他类(Employee、Manager、Boss)都继承自该抽象类 - 头文件保护:使用 pragma once 防止头文件重复包含 - 引入标准库:包含 <iostream> 和 <st…...

【AIGC】Stable Diffusion之模型微调工具
推荐一款好用的模型微调工具,cybertron furnace 是一个lora训练整合包,提供训练 lora 模型的工具集或环境。集成环境包括必要的依赖项和配置文件、预训练脚本,支持人物、二次元、画风、自定义lora的训练,以简化用户训练 lora 模型…...

探索未来科技前沿:深度学习的进展与应用
深度学习的进展 摘要:深度学习作为人工智能领域的重要分支,近年来取得了巨大的进展,并在各个领域展现出惊人的应用潜力。本文将介绍深度学习的发展历程、技术原理以及在图像识别、自然语言处理等领域的应用,展望深度学习在未来的…...

PTA | Wifi密码
下面是微博上流传的一张照片:“各位亲爱的同学们,鉴于大家有时需要使用 wifi,又怕耽误亲们的学习,现将 wifi 密码设置为下列数学题答案:A-1;B-2;C-3;D-4;请同学们自己作答…...

Linux中gdb使用说明书
首先我们要使用gdb,必须明白gdb使用范围: 要使用gdb调试,必须在源代码生成二进制程序的时候, 加上 -g 选项(gcc/g) 其次,我们就要来学习gdb使用的一些命令了: list/l 行号:显…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
