排序前言冒泡排序
目录
排序应用
常见的排序算法
BubbleSort冒泡排序
整体思路
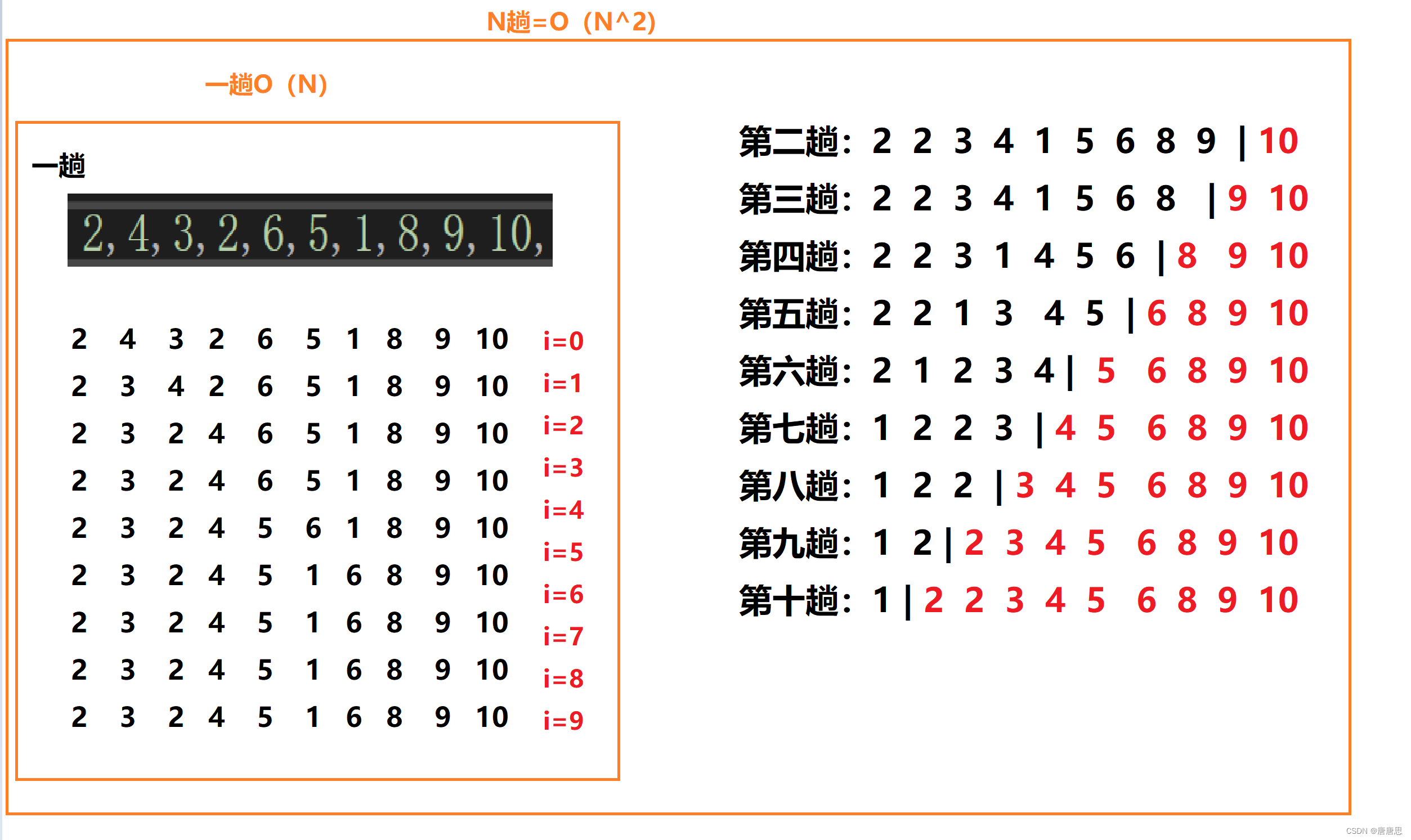
图解分析
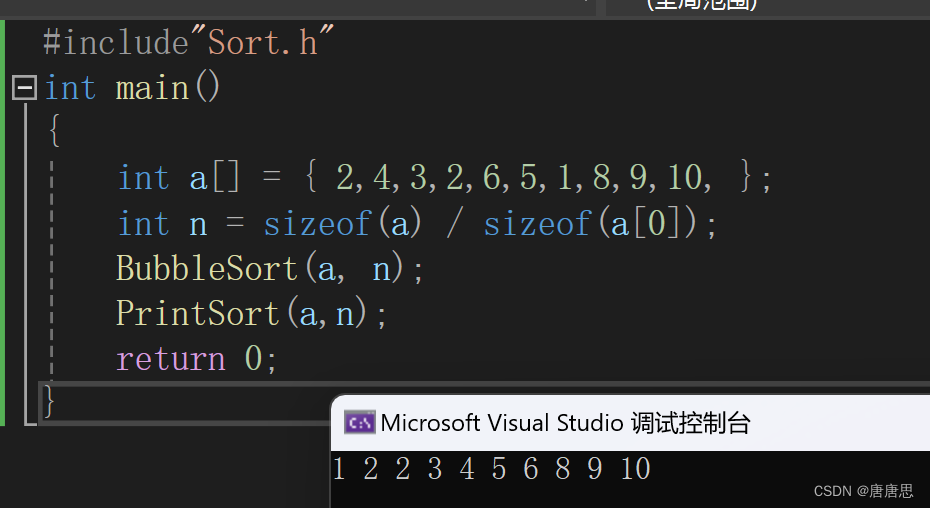
代码实现
每趟
写法1
写法2
代码NO1
代码NO2优化
时间复杂度
排序概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
- 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。
- 内部排序:数据元素全部放在内存中的排序。
- 外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
排序应用
排序的应用场景很多: 学校医院品牌的排名等等。
算法当中也常用,二分查找,去重算法等等。
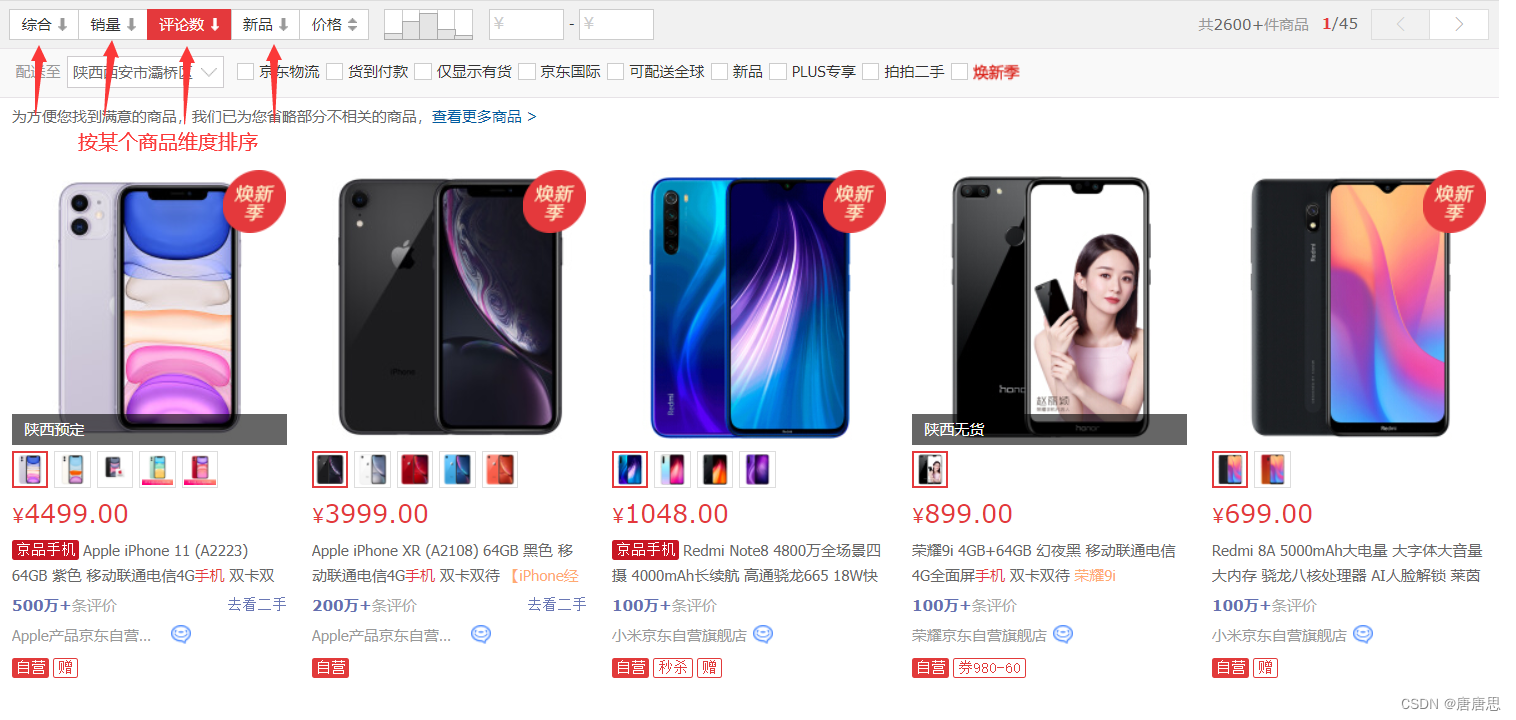
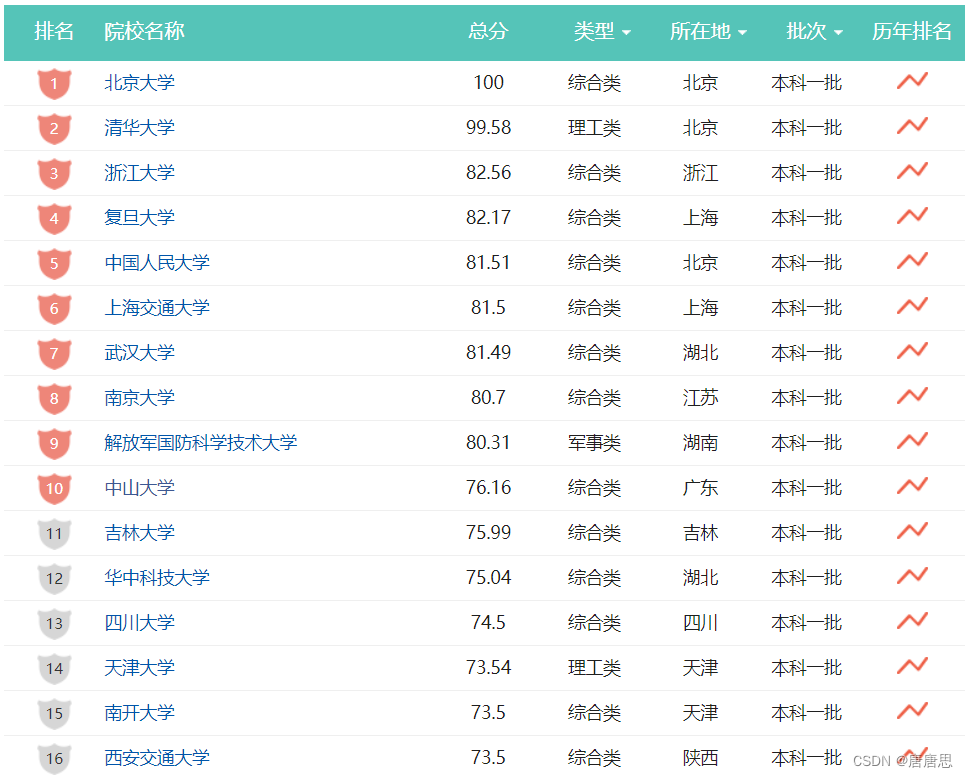
常见的排序算法

- 冒泡排序
- 直接插入排序&VS冒泡排序
- 希尔排序(在插入排序的基础上)
- 选择排序VS堆排序
- 快速排序
- 归并排序
- 补充:外排序
- 排序的OJ题目
- 排序的思想:先单趟再多趟,注意结束条件❗先局部再整体
BubbleSort冒泡排序
整体思路
- 通过对待排序序列从前向后(从下标较小的元素开始),依次对相邻两个元素的值进行两两比较,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就如果水底下的气泡一样逐渐向上冒泡。
- 一趟:两两比较(若顺序则不交换,若逆序则交换)
- 整体:重复上述过程,直到全部数组元素都每趟完成。
- 优化:若某一趟发现,数组元素已经顺序不用继续冒泡下去,停止冒泡。(效率提高)
图解分析 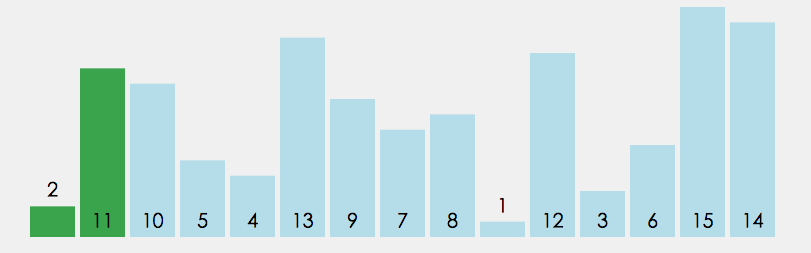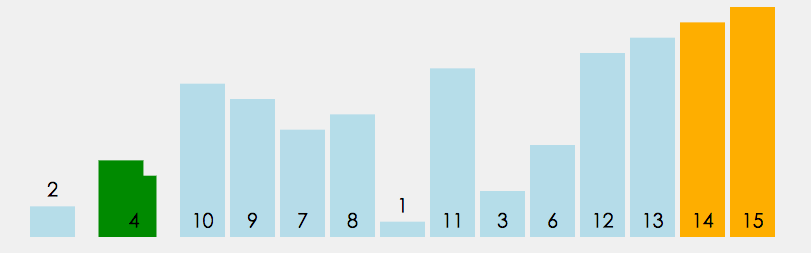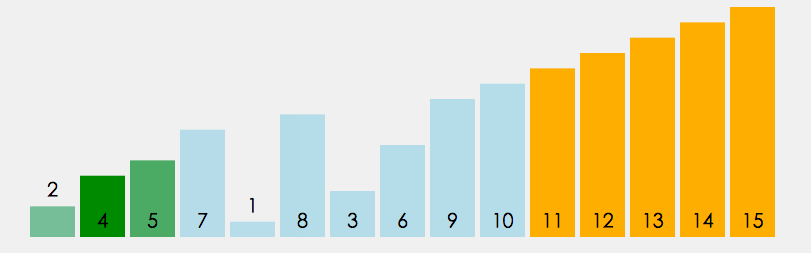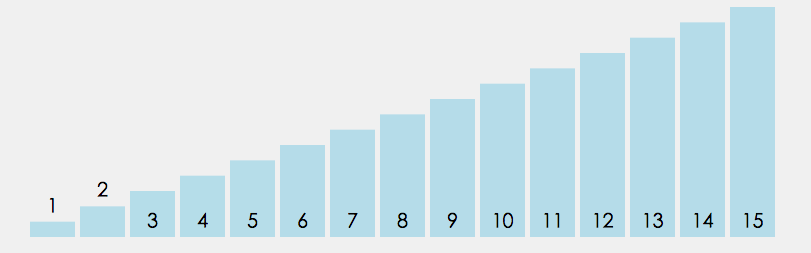
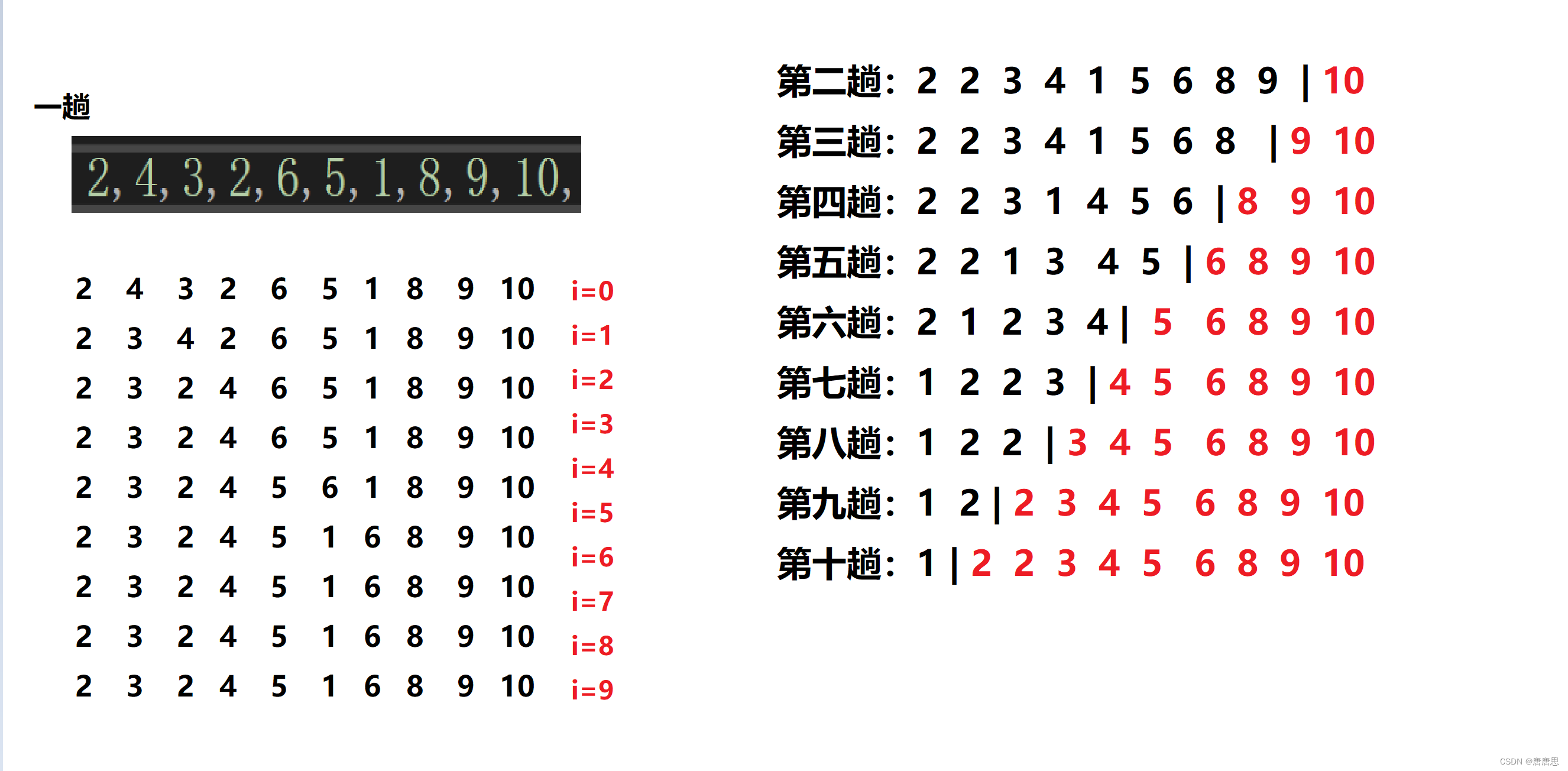
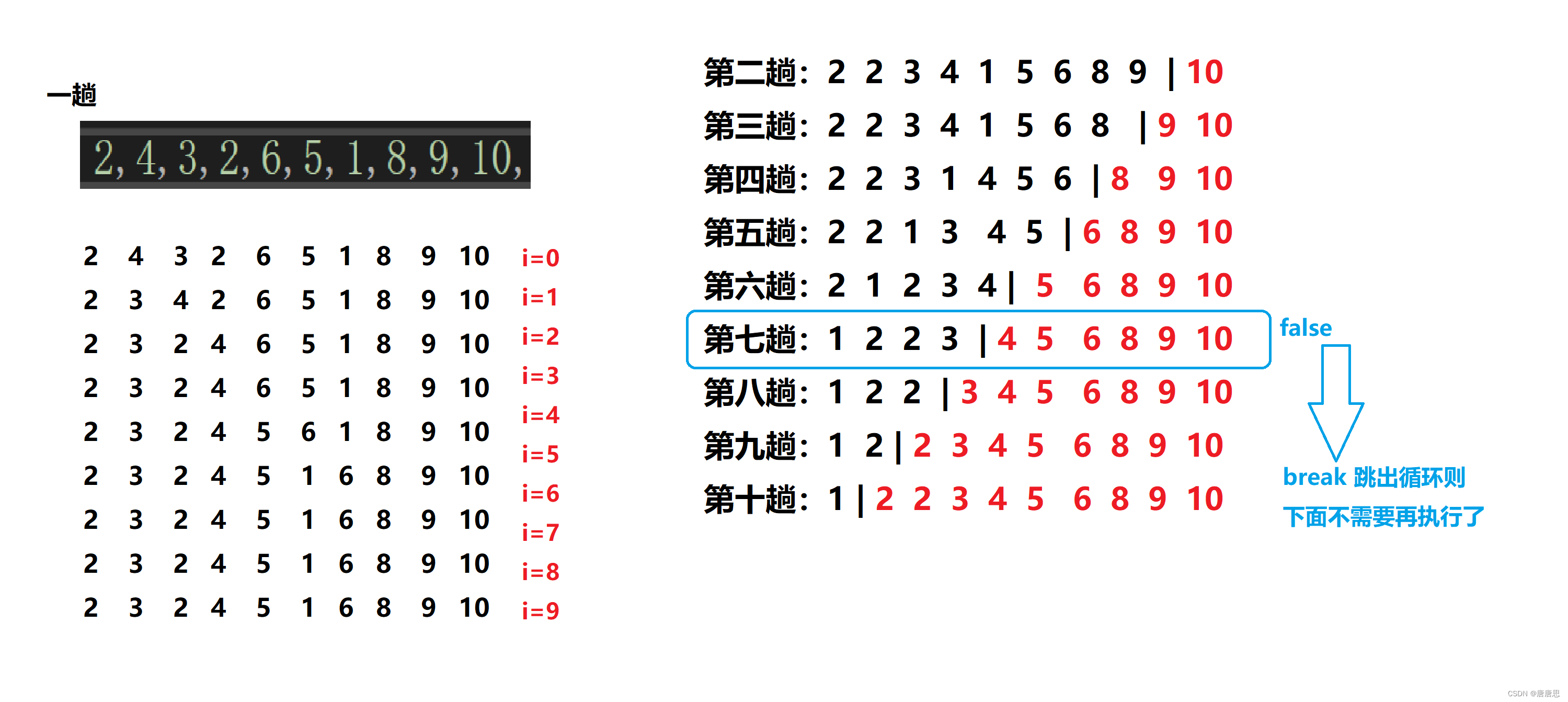
代码实现
每趟
- n个数的下标是0~n-1
- i每次从0开始,则比较的是下标为i和i+1的数值
- i每次从1开始,则比较的是下标为i-1和i的数值
- 注意:i每次从第一个数值开始冒泡,不是第j格数值开始冒泡
写法1
//写法1for (int i = 0; i < n-1; i++){if (a[i] > a[i + 1])//i=n-1就越界了{Swap(&a[i], &a[i + 1]);}}写法2
//写法2for (int i = 1; i < n; i++){if (a[i - 1] > a[i])//i=n-1没有越界,{Swap(&a[i - 1], &a[i]);}}代码NO1
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){//一趟for (int i = 0; i < n - 1 - j; i++)//i要从第一个开始交换{if (a[i] > a[i + 1])//i=n-1就越界了{Swap(&a[i], &a[i + 1]);}}}
代码NO2优化
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void BubbleSort(int* a, int n)
{for (int j = 0; j < n; j++){//一趟bool exchange = false;for (int i = 0; i < n - 1 - j; i++)//i要从第一个开始交换{if (a[i] > a[i + 1])//i=n-1就越界了{Swap(&a[i], &a[i + 1]);exchange = true;}}if (exchange == false){break;}}
}
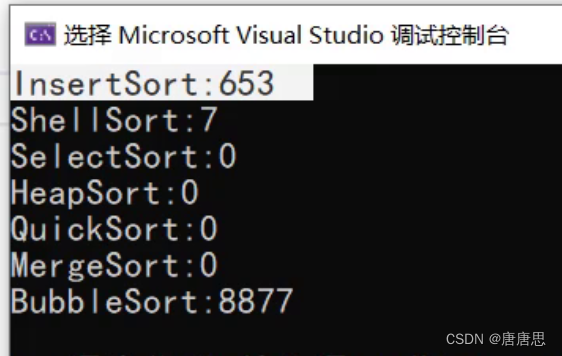
时间复杂度
时间复杂度:经典的O(N^2)
🙂感谢大家的阅读,若有错误和不足,欢迎指正!
相关文章:

排序前言冒泡排序
目录 排序应用 常见的排序算法 BubbleSort冒泡排序 整体思路 图解分析 代码实现 每趟 写法1 写法2 代码NO1 代码NO2优化 时间复杂度 排序概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递…...

红队笔记Day3-->隧道上线不出网机器
昨天讲了通过代理的形式(端口转发)实现了上线不出网的机器,那么今天就来讲一下如何通过隧道上线不出网机器 目录 1.网络拓扑 2.开始做隧道?No!!! 3.icmp隧道 4.HTTP隧道 5.SSH隧道 1.什么…...

C 练习实例70-求字符串长度
题目:写一个函数,求一个字符串的长度,在 main 函数中输入字符串,并输出其长度。 解答: #include <stdio.h> int length(char *s); int main() {int len;char str[20];printf("请输入字符串:\n");scan…...

HarmonyOS—@State装饰器:组件内状态
State装饰的变量,或称为状态变量,一旦变量拥有了状态属性,就和自定义组件的渲染绑定起来。当状态改变时,UI会发生对应的渲染改变。 在状态变量相关装饰器中,State是最基础的,使变量拥有状态属性的装饰器&a…...
Linux系统——防火墙拓展及重点理解
目录 一、iptables 1.基本语法 2.四表五链——重点记忆 2.1四表 2.2五链 2.3总结 3.iptables选项示例 3.1 -Z 清空流量计数 3.2 -P 修改默认规则 3.3 -D 删除规则 3.4 -R 指定编号替换规则 5.白名单 6.通用匹配 7.示例 7.1添加回环网卡 7.2可以访问端口 7.3 主…...

阿里云短信验证码的两个坑
其它都参照官网即可,其中有两个坑需要注意: 1、除去官网pom引用的包之外,还需要引用以下包: <dependency><groupId>org.apache.httpcomponents.client5</groupId><artifactId>httpclient5</artifact…...
)
c入门第十五篇——学而时习之(阶段性总结)
古人说:“学而时习之。”古人又说:“温故而知新。”古人还说:“读书百遍,其义自见。” 总结一个道理那就是好书要反反复复的读,学习过的知识要时常去复习它,才有可能常读常新。 我:“师弟&…...

抽象的前端
问题背景:vue3,axios 直接导致问题:路由渲染失败 问题报错:Uncaught SyntaxError: The requested module /node_modules/.vite/deps/axios.js?v7bee3286 does not provide an export named post (at LoginIn.vue:16:9) 引入组…...

UPC训练赛二十/20240217
A:无穷力量 题目描述 2022年重庆突发山火让世界看到了中国一个又一个的感人事迹:战士们第一时间奔赴火场,志愿者们自发组成团队,为救火提供一切的可能的服务,人们自发输送物资,有的志愿者甚至几天几夜没有睡觉。每个…...
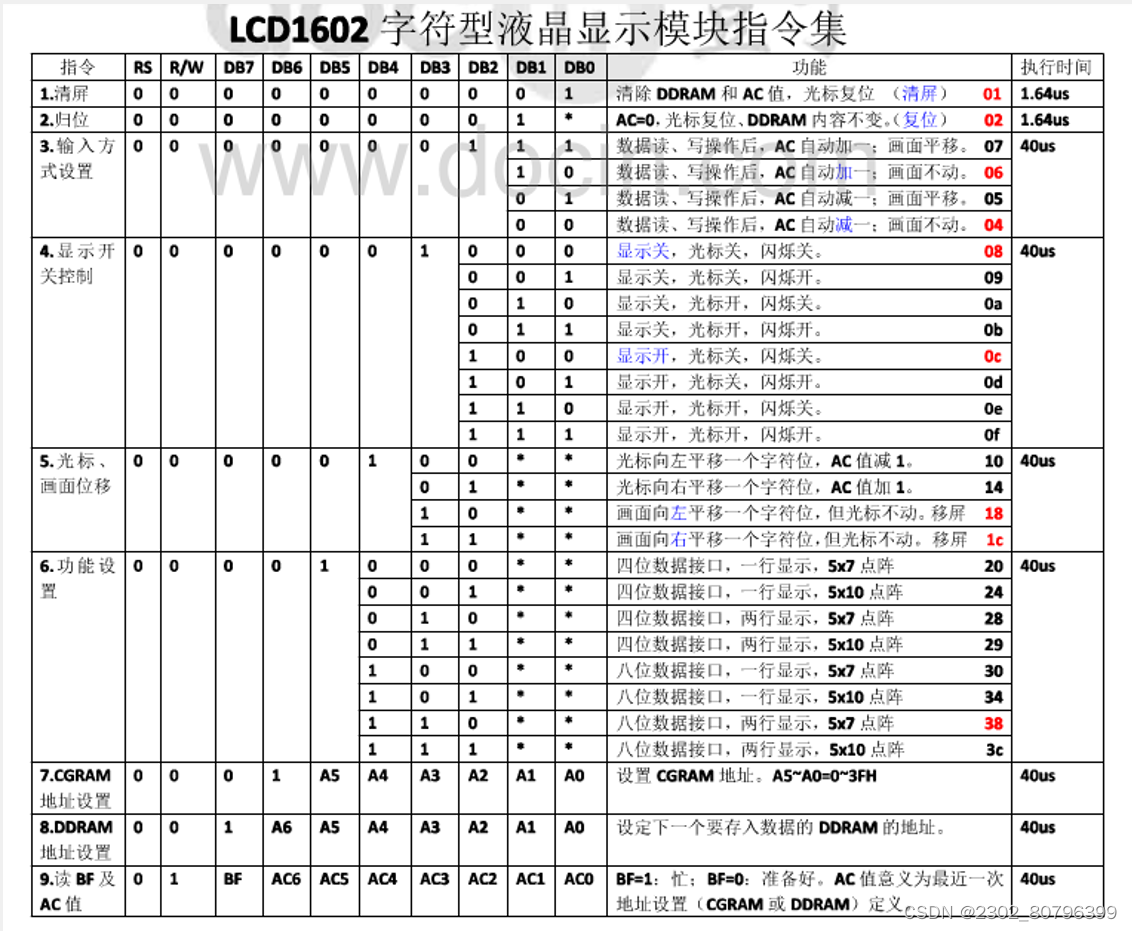
【51单片机】LCD1602(江科大)
1.LCD1602介绍 LCD1602(Liquid Crystal Display)液晶显示屏是一种字符型液晶显示模块,可以显示ASCII码的标准字符和其它的一些内置特殊字符,还可以有8个自定义字符 显示容量:162个字符,每个字符为5*7点阵 2.引脚及应用电路 3.内部结构框图 屏幕: 字模库:类似于数码管的数…...

conda与pip的常用命令
conda的常用命令 1.查看conda版本 $ conda --version conda 23.11.02.查看conda的配置信息 $ conda infoactive environment : baseactive env location : /home/myPc/miniconda3shell level : 1user config file : /home/myPc/.condarcpopulated config files : conda vers…...

你知道什么是物联网MQTT么?
目录 你知道什么是物联网MQTT么?MQTT的基本概念MQTT的工作原理MQTT的应用场景MQTT的实例案例智能家居场景工业监控场景 你知道什么是物联网MQTT么? MQTT(Message Queuing Telemetry Transport)是一种轻量级的、基于发布/订阅模式…...

P8 pair vector
pair是一个模板类,用于表示一对值的组合,用<utility>中 pair模板有两个模板参数,t1 t2,分别表示第一个值和第二个值类型 pair类有两个成员变量,frist和 cond,分别表示第一个值与第二个值 还有一些成员函数和…...

奇异值分解(SVD)的应用——图像压缩
SVD方法是模型降阶的一类重要方法,本征正交分解(POD)和平衡截断(BT)都属于SVD类方法。 要想深入了解模型降阶技术,我们可以先从SVD的应用入手,做一个直观的了解。 1. SVD的定义和分类 我们想寻找…...

RTDETR改进系列指南
基于Ultralytics的RT-DETR改进项目.(89.9) 为了感谢各位对RTDETR项目的支持,本项目的赠品是yolov5-PAGCP通道剪枝算法.具体使用教程 自带的一些文件说明 train.py 训练模型的脚本main_profile.py 输出模型和模型每一层的参数,计算量的脚本(rtdetr-l和rtdetr-x因为thop库的问…...

类和结构体的区别
类(class)和结构体(struct)是面向对象编程(Object-Oriented Programming,OOP)中常见的两种数据类型,它们在不同的编程语言中有一些共同之处,但也存在一些区别。以下是它们…...

利用Excel模拟投币试验
文章目录 试验前对Excel要进行的设置试验步骤计算正面频率结果图试验前对Excel要进行的设置 进入Excel依次点击如下选项,最后将分析工具库勾选 #mermaid-svg-bIvrxZGI9buCMW6U {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#m…...

WebService接口测试
WebService的理解 WebService就是Web服务的意思,对应的应用层协议为SOAP(相当于HTTP协议),可理解为远程调用技术。 特点: 客户端发送的请求主体内容(请求报文)的格式为XML格式 接口返回的响…...
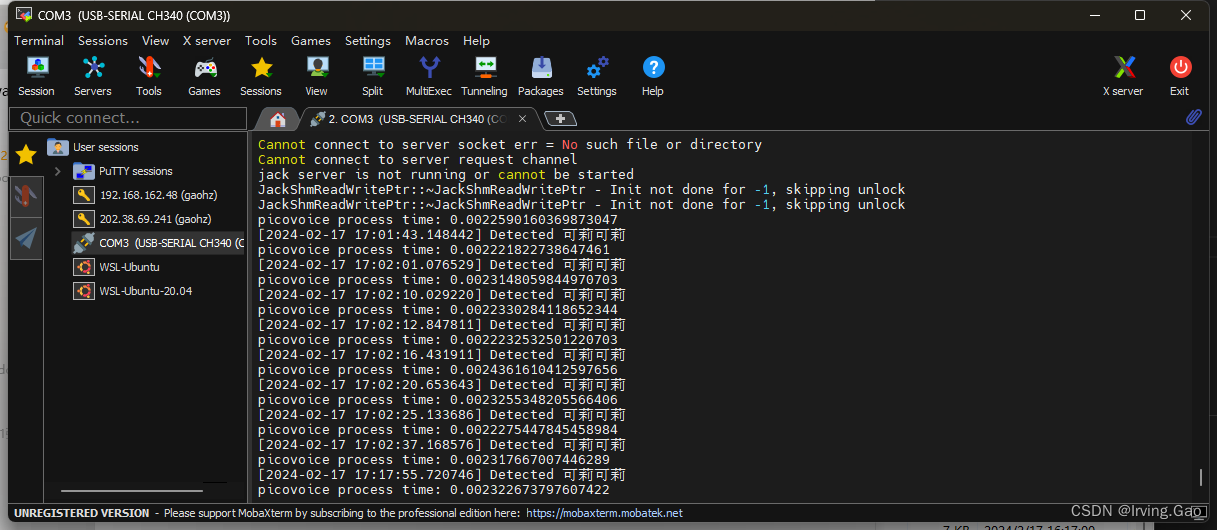
语音唤醒——
文章目录 配置主代码 参考文档:https://picovoice.ai/docs/quick-start/porcupine-python/ 配置 pip install pvporcupine主代码 ACCESS_KEY:需要将该参数填入即可 # # Copyright 2018-2023 Picovoice Inc. # # You may not use this file except in …...
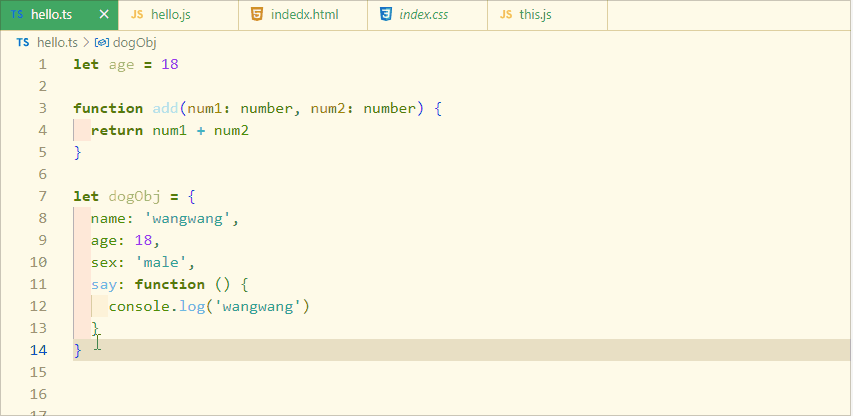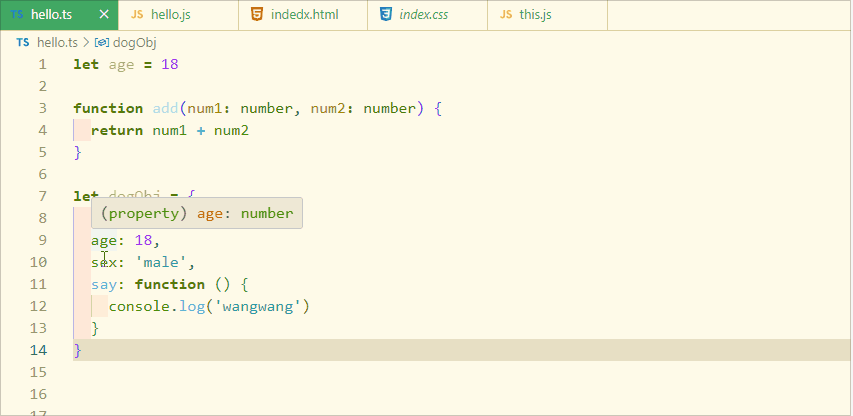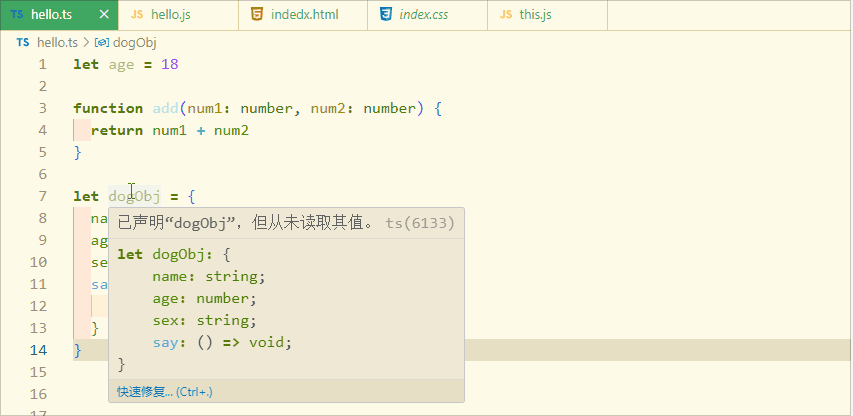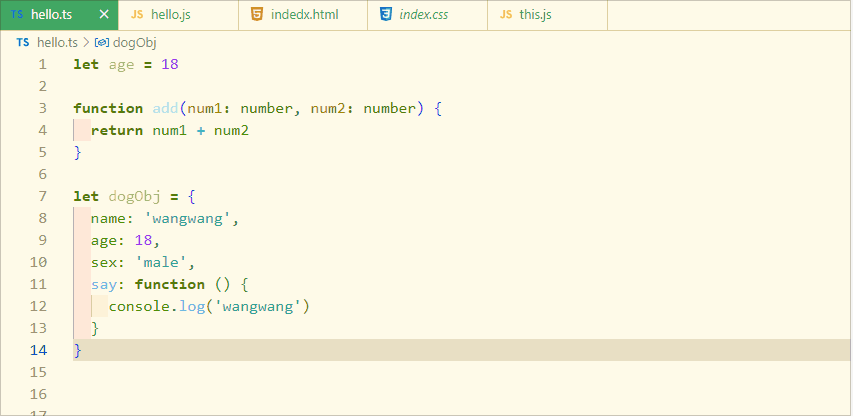
typeScript 类型推论
什么是类型推论? 类型推论是 TypeScript 中的一个特性,它允许开发人员不必显式地指定变量的类型。相反,开发人员可以根据变量的使用情况让 TypeScript 编译器自动推断出类型。例如,如果开发人员将一个字符串赋值给一个变量&#…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
