ABC341A-D题解
文章目录
- A
- 题目
- AC Code:
- B
- 题目
- AC Code:
- C
- 题目
- AC Code:
- D
- 题目
- 你以为这就完了?
- 时间复杂度分析:
- AC Code:
- E
A
题目
这个没什么好说的,就先输出一个 1,再输出 n n n 个 01就大功告成了。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
int n;int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n;cout << 1;for (int i = 1; i <= n; i ++) cout << "01";return 0;
}
B
题目
要获取更多 x x x 国货币,只能用 x − 1 x - 1 x−1 国货币换。
所以我们可以从 1 1 1 国一直换到 n n n 国,输出,结束。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
int n;
long long a[200100];
int s[200100], t[200100];int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n;for (int i = 1; i <= n; i ++) cin >> a[i];for (int i = 1; i < n; i ++) cin >> s[i] >> t[i];for (int i = 1; i < n; i ++) {a[i + 1] += t[i] * (a[i] / s[i]);}cout << a[n];return 0;
}
C
题目
你会发现, 50 0 3 < 2 ⋅ 1 0 8 500^3<2\cdot10^8 5003<2⋅108,所以可以暴力枚举高桥所在的位置,如果他行进的过程中没有经过海洋就将答案加一。如果经过海洋了就直接枚举下一个点。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
int h, w, n;
char m[510][510];
string s;
map<char, int> dir;
int dx[4] = {0, 0, -1, 1}, dy[4] = {-1, 1, 0, 0};
int ans;
bool check(int x, int y) {for (int i = 0; i < n; i ++) {int nx = x + dx[dir[s[i]]], ny = y + dy[dir[s[i]]];if (nx > 0 && nx <= h && ny > 0 && ny <= w && m[nx][ny] == '.') {x = nx;y = ny;}else return 0;}return 1;
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> h >> w >> n;cin >> s;for (int i = 1; i <= h; i ++) {for (int j = 1; j <= w; j ++) cin >> m[i][j];}dir['L'] = 0, dir['R'] = 1, dir['U'] = 2, dir['D'] = 3;for (int i = 1; i <= h; i ++) {for (int j = 1; j <= w; j ++) {if (m[i][j] == '.') {ans += check(i, j);}}}cout << ans;return 0;
}
D
题目
这个题并不难,但是细节很多,仔细看!我因为一些零碎的细节卡了 40min!
首先,我们先讨论那些“有规律”的部分。我们发现,对于两个数 n n n 和 m m m,在 n m nm nm 范围内有 n + m − 2 × gcd ( n , m ) n + m - 2\times\gcd(n, m) n+m−2×gcd(n,m) 个数满足只被 n n n 和 m m m 中的一个数字整除。
这个结论怎么来的呢?
首先,对于可以被 n n n 整除的一共有 n m n \frac{nm}{n} nnm 共 m m m 个,可以被 m m m 整除的一共有 n m m \frac{nm}{m} mnm 共 n n n 个。
那么 − 2 × gcd ( n , m ) -2\times\gcd(n, m) −2×gcd(n,m) 又是怎么来的呢?
首先, n m nm nm 范围内有 n m n m gcd ( n , m ) \frac{nm}{\frac{nm}{\gcd(n, m)}} gcd(n,m)nmnm 个数即 gcd ( n , m ) \gcd(n,m) gcd(n,m) 个数可以被 n n n 和 m m m 整除。我们要在可以被 n n n 整除的部分减去它,还要在可以被 m m m 整除的部分减去它。所以是 − 2 × gcd ( n , m ) -2\times\gcd(n,m) −2×gcd(n,m)。
然后我们就可以将答案直接跳到 n m ( k / ( n + m − 2 gcd ( n , m ) ) ) nm(k/(n + m - 2\gcd(n, m))) nm(k/(n+m−2gcd(n,m))),此时 k k k 变成 k m o d ( n + m − 2 gcd ( n , m ) ) k \mod (n + m - 2\gcd(n, m)) kmod(n+m−2gcd(n,m))。
我们继续讨论,可以枚举,用 k 1 k1 k1 和 k 2 k2 k2 两个变量依次跳到答案。如果 k 1 k1 k1 跳的远就跳 k 2 k2 k2,否则跳 k 1 k1 k1。如果两个跳的一样远就都跳依次,这两次不算在跳的次数内。一共跳 k k k 次后,较大的就是满足条件的,加到答案上即可。
你以为这就完了?
如果减掉前面“有规律”的部分后,发现 k k k 等于 0 0 0 时,不加任何特判会输出一个 n m nm nm 的倍数的数。但是我们要的是最大的比上述不合法答案小的答案。此时如果我们把 k k k 设为 n + m − 2 gcd ( n , m ) n+m-2\gcd(n, m) n+m−2gcd(n,m),答案减去 n m nm nm 就可以解决这个问题。
还有一个很重要的东西:long long!
时间复杂度分析:
按最坏情况来说, gcd ( n , m ) = 1 \gcd(n, m)=1 gcd(n,m)=1,此时时间复杂度就是 n + m n+m n+m,而且跑不到这么多,所以执行次数不会超过 2 ⋅ 1 0 8 2\cdot10^8 2⋅108,合格。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
long long n, m, k;
long long gcd(long long x, long long y) {return x % y == 0ll ? y : gcd(y, x % y);
}
long long ans;
long long cnt;
long long cnt1;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m >> k;long long g = gcd(n, m);ans = n * m * (k / (n + m - g * 2));k = k % (n + m - g * 2);if (k == 0) {ans -= n * m;k += n + m - g * 2;}long long k1 = 0ll, k2 = 0ll;cnt1 = 0ll;for (long long i = 1; i <= k; i ++) {if (k1 + n < k2 + m) {k1 += n;}else if (k1 + n > k2 + m) {k2 += m;}else {k1 += n;k2 += m;i--;}}ans += max(k1, k2);cout << ans;return 0;
}
E
什么,不是 A-D题解吗?怎么还有 E?
我才不会给出详细的解法的,我只给一个小小的提示:懒标线段树!
相关文章:

ABC341A-D题解
文章目录 A题目AC Code: B题目AC Code: C题目AC Code: D题目你以为这就完了? 时间复杂度分析:AC Code: E A 题目 这个没什么好说的,就先输出一个 1,再输出 n n n 个 01就大功告成…...

计算机网络——07协议层次及服务模型
协议层次及服务模型 协议层次 网络是一个复杂的系统 网络功能复杂:数字信号的物理信号承载、点到点、路由、rdt、进程区分、应用等现实来看,网络的许多构成元素和设备: 主机路由器各种媒体的链路应用协议硬件,软件 问题是&am…...

Netty Review - NIO空轮询及Netty的解决方案源码分析
文章目录 Pre问题说明NIO CodeNetty是如何解决的?源码分析入口源码分析selectCntselectRebuildSelector Pre Netty Review - ServerBootstrap源码解析 Netty Review - NioServerSocketChannel源码分析 Netty Review - 服务端channel注册流程源码解析 问题说明 N…...

PAM | 账户安全 | 管理
PAM PAM(Pluggable Authentication Modules,可插入式身份验证模块)是一个灵活的身份验证系统,允许我们通过配置和组合各种模块来实现不同的身份验证策略。 在 Linux 或类 Unix 系统中,常见的 PAM 模块包括以下几种类…...

Leetcode 16-20题
最接近的三数之和 给定整数数组和目标值target,从数组中选出三个整数,使得和与target最接近,并返回三数之和。保证恰好存在一个解。 和上一题类似,我们先对整数数组排序,然后固定i,枚举j,找到满…...
项目的15 个开源训练数据集)
【开源训练数据集1】神经语言程式(NLP)项目的15 个开源训练数据集
一个聊天机器人需要大量的训练数据,以便在无需人工干预的情况下快速解决用户的询问。然而,聊天机器人开发的主要瓶颈是获取现实的、面向任务的对话数据来训练这些基于机器学习的系统。 我们整理了训练聊天机器人所需的对话数据集,包括问答数据、客户支持数据、对话数据和多…...

【AIGC】Stable Diffusion的ControlNet参数入门
Stable Diffusion 中的 ControlNet 是一种用于控制图像生成过程的技术,它可以指导模型生成特定风格、内容或属性的图像。下面是关于 ControlNet 的界面参数的详细解释: 低显存模式 是一种在深度学习任务中用于处理显存受限设备的技术。在这种模式下&am…...
)
静态curl库编译与使用(c++)
静态curl库编译与使用 静态curl库编译与使用:mingw https://curl.se/windows/ // 测试:设置URL地址 // curl_easy_setopt(curlHandle, CURLOPT_URL, “https://ipinfo.io/json”); // curl_easy_setopt(curlHandle, CURLOPT_SSL_VERIFYPEER, 0L); // c…...

element 表单提交图片(表单上传图片)
文章目录 使用场景页面效果前端代码 使用场景 vue2 element 表单提交图片 1.点击【上传图片】按钮择本地图片(只能选择一张图片)后。 2.点击图片,支持放大查看。 3.点击【保存】按钮,提交表单。 页面效果 前端代码…...
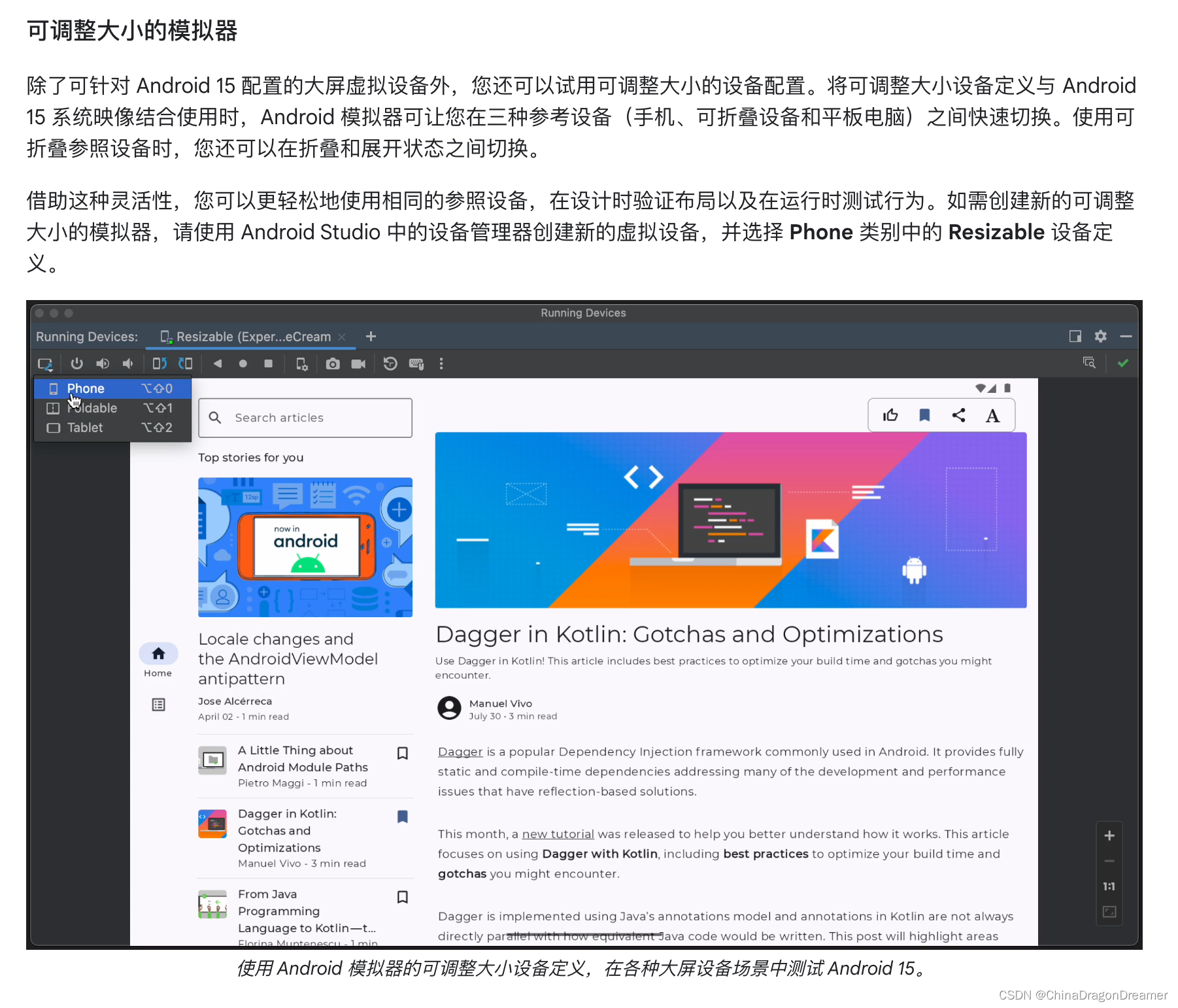
Android 15 第一个开发者预览版
点击查看:first-developer-preview-android15 点击查看:Get Android 15 2024年2月16日,谷歌发布 Android 15 第一个开发者预览版 翻译 由工程副总裁戴夫伯克发布 今天,我们发布了Android 15的首个开发者预览版,这样我们的开发者就…...
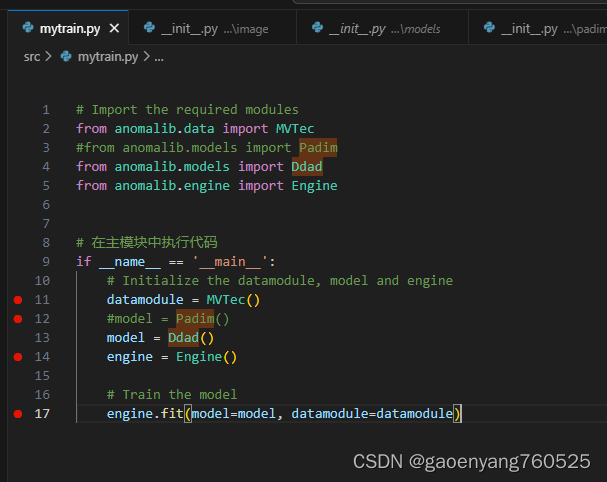
anomalib1.0学习纪实-续1:增加新算法
0、基本信息 现在我要增加一个新算法:DDAD 他的代码,可以在github中找到:GitHub - arimousa/DDAD 一、基础操作: 1、修改anomalib\src\anomalib\models\__init__.py 我增加的第33行和61行, 2、 增加ddad文件夹和文…...

Java+Vue+MySQL,国产动漫网站全栈升级
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...

机器人常用传感器分类及一般性要求
机器人传感器的分类 传感技术是先进机器人的三大要素(感知、决策和动作)之一。根据用途不同,机器人传感器可以分为两大类:用于检测机器人自身状态的内部传感器和用于检测机器人相关环境参数的外部传感器。 内部传感器 内部传感…...
C++-opencv的imread、imshow、waitkey、namedWindow
在C中使用OpenCV时,imread和imshow是两个非常基础且常用的函数,用于读取图像和显示图像。以下是这两个函数的简要说明和如何一起使用它们的示例。 imread函数 imread用于从指定的文件路径读取图像。它将图像读入为cv::Mat对象,这是OpenCV中…...

开源语音识别faster-whisper部署教程
1. 资源下载 源码地址 模型下载地址: large-v3模型:https://huggingface.co/Systran/faster-whisper-large-v3/tree/main large-v2模型:https://huggingface.co/guillaumekln/faster-whisper-large-v2/tree/main large-v2模型:…...
)
使用IntelliJ IDEA配置Maven (入门)
在使用IntelliJ IDEA进行Java开发时,配置Maven是至关重要的一步,因为它可以帮助你管理项目的依赖和构建过程。以下是我在使用IntelliJ IDEA配置Maven的实践过程,以及一些技术笔记和职场感悟。 工作实践与项目复盘 下载Maven: 访问…...
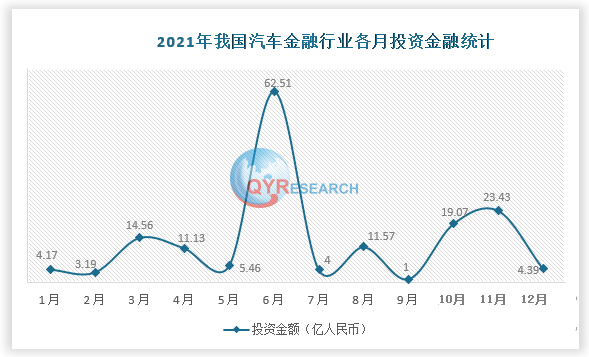
汽车金融市场研究:预计2029年将达到482亿美元
汽车金融公司作为汽车流通产业链的重要一环,认真贯彻落实国家有关政策,采取多种措施助力汽车产业发展,为促进推动汽车消费、助力畅通汽车产业链、支持稳定宏观经济大盘发挥了积极作用。 益于国内疫情得到有效控制,我国经济持续稳定…...

关于举办第十五届蓝桥杯大赛电子赛5G全网规划与建设赛项的通知
关于举办第十五届蓝桥杯大赛电子赛 5G全网规划与建设赛项的通知 各相关院校: 第十五届蓝桥杯大赛通知已于2023年9月27日在蓝桥杯大赛官网发布,现就电子赛5G全网规划与建设赛项报名事宜,公布如下: 一、赛项概述 5G全网规划与建设…...

Vue3快速上手(七) ref和reactive对比
一、ref和reactive对比 表格形式更加直观吧: 项目refreactive是否支持基本类型支持不支持是否支持对象类型支持支持对象类型是否支持属性直接赋值不支持,需要.value支持是否支持直接重新分配对象支持,因为操作的.value不支持,需…...

8、内网安全-横向移动RDPKerberos攻击SPN扫描WinRMWinRS
用途:个人学习笔记,有所借鉴,欢迎指正 目录 一、域横向移动-RDP-明文&NTLM 1.探针服务: 2.探针连接: 3.连接执行: 二、域横向移动-WinRM&WinRS-明文&NTLM 1.探针可用: 2.连接…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
