二叉树相关OJ题
创作不易,感谢三连!!
一、选择题
1、某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A.不存在这样的二叉树
B.200
C.198
D.199
解析:选B,根据n0=n2+1的结论(这个结论不清楚的看博主的关于二叉树概念的文章有证明),就是度为0的节点始终比度为2的节点多一个,所以这题就很显然选B了!!
2、在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
解析:选A ,原因如下

3、一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
解析:选B,根据结论——满二叉树的节点N数量=2^h-1,如果高度为8,那么节点最多有255个,当高度为10时,节点最多有1023个,所以高度只能是10
4、一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
解析:选B,因为度为2的节点数肯定并度为0的节点数少1个,所以n0和n2一个是奇数一个是偶数,所以n1只能是偶数,又因为完全二叉树n1只有可能是0或者1,所以n1只能取0,所以n0=384,n2=383
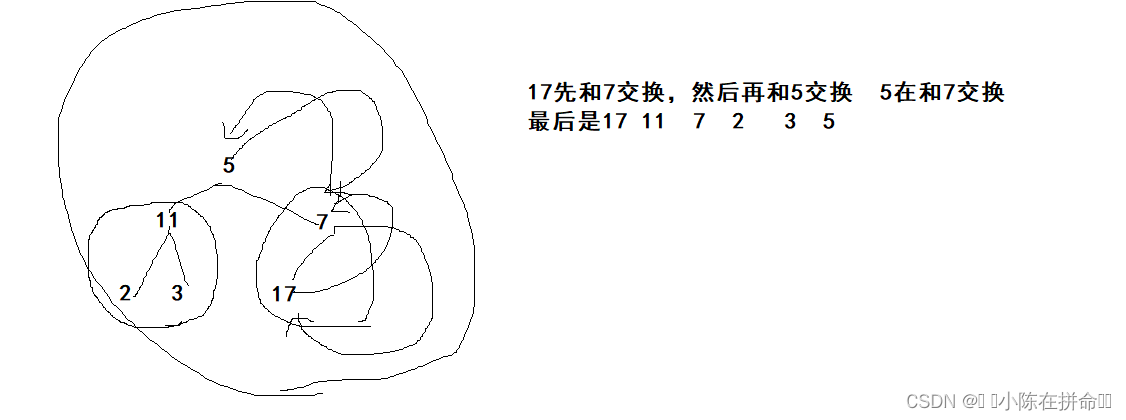
5、一组记录排序码为(5 11 7 2 3 17),则利用堆排序方法建立的初始堆为()。
A(11 5 7 2 3 17)
B(11 5 7 2 17 3)
C(17 11 7 2 3 5)
D(17 11 7 5 3 2)
E(17 7 11 3 5 2)
F(17 7 11 3 2 5)
解析:选C 先画出来,再不断向下调整
6、最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后,其结果是()
A[3,2,5,7,4,6,8]
B[2,3,5,7,4,6,8]
C[2,3,4,5,7,8,6]
D[2,3,4,5,6,7,8]
解析:选C,还是画出来再调整
二、单值二叉树
OJ:单值二叉树


bool isUnivalTree(struct TreeNode* root)
{if(root==NULL)//a==b,a==c,->b==creturn true;if(root->left&&root->left->val!=root->val)return false;if(root->right&&root->right->val!=root->val)return false;return isUnivalTree(root->left)&&isUnivalTree(root->right);
}三、检查两棵树是否相同
OJ:判断两棵树是否相同

这个在博主讲解二叉树链式存储中有仔细分析过了!!
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{if(p==NULL&&q==NULL)return true;if(p==NULL||q==NULL)return false;if(p->val!=q->val)return false;//此时得到的节点存在,且节点值相同的情况return isSameTree(p->left, q->left) &&isSameTree(p->right, q->right);
}四、对称二叉树
OJ:对称二叉树


bool _isSymmetric(struct TreeNode* leftroot,struct TreeNode* rightroot)
{//都为空,对称if(leftroot==NULL&&rightroot==NULL)return true;//一个为空一个不为空,不对称if(leftroot==NULL||rightroot==NULL)return false;//都不为空,就可以看值了,如果值不相等,不对称if(leftroot->val!=rightroot->val)return false;//此时都不为空,且值相等,就走递归找下一个//左树的左子树要跟右树的右子树相比//左树的右子树要跟右树的左子树相比return _isSymmetric(leftroot->left,rightroot->right)&&_isSymmetric(leftroot->right,rightroot->left);
}bool isSymmetric(struct TreeNode* root)
{if(root==NULL)return true;//根不对称,就去找左右子树比 相当于是拆成两棵树的了return _isSymmetric(root->left,root->right);
}五、二叉树的前序遍历
OJ:二叉树的前序遍历

int TreeSize(struct TreeNode* root)
{return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
void _preorder(struct TreeNode* root,int *a,int *i)
{if(root==NULL)return ;a[(*i)++]=root->val;_preorder(root->left,a,i);_preorder(root->right,a,i);
}int* preorderTraversal(struct TreeNode* root, int* returnSize)
{//returnsize是结点数*returnSize=TreeSize(root);int *a=(int *)malloc(*returnSize*sizeof(int));int i=0;_preorder(root,a,&i);return a;
}
六、二叉树的中序遍历
OJ:二叉树的中序遍历
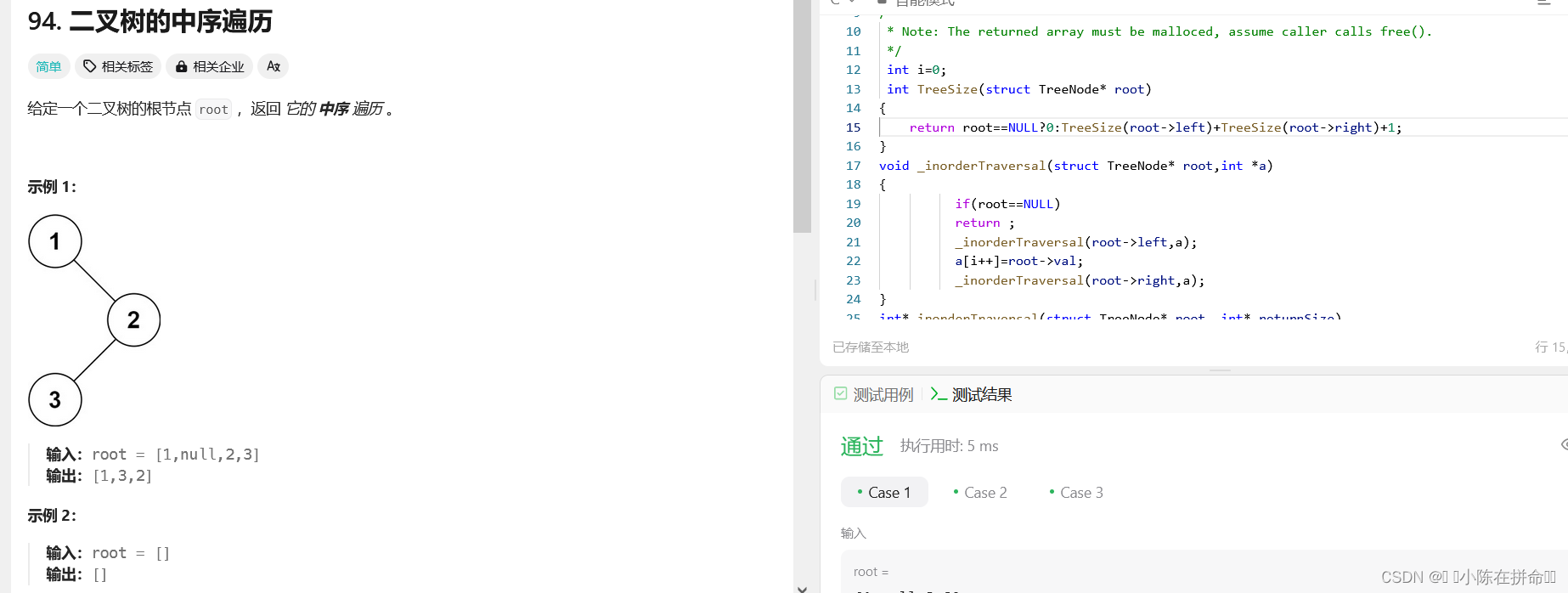
int i=0;int TreeSize(struct TreeNode* root)
{return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
void _inorderTraversal(struct TreeNode* root,int *a)
{if(root==NULL)return ;_inorderTraversal(root->left,a);a[i++]=root->val;_inorderTraversal(root->right,a);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{//returnsize是结点数*returnSize=TreeSize(root);int *a=(int *)malloc(*returnSize*sizeof(int));i=0;//全局变量一定要记得赋0_inorderTraversal(root,a);//必须构造新函数去递归,因为在原函数递归会不断创建新的数组return a;
}注:这题跟上题是差不多的,我稍微改了一下,这里数组的下标我不用指针去接受参数了,而是直接设置一个全局变量i!!要注意的是,因为力扣的测试可能会多次调用这个函数,所以我们一定要在递归函数运行前让i=0!!否则就会i就会一直叠加下去导致越界!! (还有一个注意事项就是,这里千万不要使用静态的局部变量,虽然他也同样可以在函数栈帧销毁时不被释放,但是他的作用域很小,不能让我们在主函数中让i=0)
但是尽量少使用全局变量!!
七、二叉树的后序遍历
OJ:二叉树的后序遍历

void _postorder(struct TreeNode* root,int *arr,int *arrsize)
{if(root==NULL)return;_postorder(root->left,arr,arrsize);_postorder(root->right,arr,arrsize);arr[(*arrsize)++]=root->val;
}int* postorderTraversal(struct TreeNode* root, int* returnSize)
{int *arr=(int*)malloc(100*sizeof(int));*returnSize=0;_postorder(root,arr,returnSize);return arr;
}注:这题和前两题差不多,但是又进行了改进,我们发现了题目的一个条件

也就是说我们动态开辟100个空间的话是绝对不会越界的,所以就不需要通过自己封装一个treesize函数来计算节点个数数量了!! 那我们要怎么去让returnsize返回节点个数的值的??方法就是把*returnsize初始化为0作为下标,每次放进一个值的时候*returnsize就会++一次,当后序遍历结束的时候,returnsize恰好又多+了一次,正好表示节点个数的数量!!
八、另一颗树的子树
OJ:另一颗树的子树



bool isSametree(struct TreeNode* p,struct TreeNode* q)//比较两个树的递归函数
{if(p==NULL&&q==NULL)return true;if(p==NULL||q==NULL)return false;if(p->val!=q->val)return false;return isSametree(p->left,q->left)&&isSametree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{if(root==NULL)return false;//为空就不比较的,因为subRoot是至少有一个节点的。if(isSametree(root,subRoot))return true;return isSubtree(root->left, subRoot)||isSubtree(root->right, subRoot);//左子树和右子树只要有一个找到了,就返回true
}关键就是我们每遍历到一个节点,都要尝试把他往下遍历去和另外一个子树进行比较!!所以单独封装了一个比较两个树是否相同的函数,该树每遍历一次节点就去调用一次,最后在用||操作符,因为左子树和右子树只要有一个找到就可以了!!
九、二叉树的构建及遍历
OJ:二叉树的构建及遍历

typedef char BTDataType;
typedef struct BTtreeNode
{BTDataType val;struct BTtreeNode*left;struct BTtreeNode*right;
}BTtreeNode;BTtreeNode* BuyNode(BTDataType x)
{BTtreeNode*newnode=(BTDataType*)malloc(sizeof(BTDataType));newnode->left=newnode->right=NULL;newnode->val=x;if(newnode==NULL){perror("malloc fail");exit(1);}return newnode;
}BTtreeNode* CreateTree(BTDataType*a,int *pi)
{if(a[*pi]=='#'){(*pi)++;return NULL;}BTtreeNode*root=BuyNode(a[(*pi)++]);root->left=CreateTree(a,pi);root->right=CreateTree(a,pi);return root;
}void InOrder(BTtreeNode*root)
{if(root==NULL)return;InOrder(root->left);printf("%c ",root->val);InOrder(root->right);
}int main()
{char arr[100];scanf("%s",arr);int i=0;BTtreeNode*root=CreateTree(arr,&i);InOrder(root);printf("\n");return 0;
}这题就是将二叉树的构建和链式结构的中序遍历结合起来了!!
相关文章:

二叉树相关OJ题
创作不易,感谢三连!! 一、选择题 1、某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( ) A.不存在这样的二叉树 B.200 C.198 D.199解析:选B&…...
文物保护系统守护历史岁月,成都青铜展科技闪耀
一、“吉金万里-中国西南青铜文明展”隆重开幕 1月27日,“吉金万里-中国西南青铜文明展”在成都金沙遗址博物馆向公众开放,奉上一场精彩的青铜文明“盛宴”。本次展览汇集了中国西南地区32家文博单位,以青铜器为代表的294件经典文物…...
[计算机网络]---Http协议
前言 作者:小蜗牛向前冲 名言:我可以接受失败,但我不能接受放弃 如果觉的博主的文章还不错的话,还请点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正 本期学习…...

Hexo删除主题
一、找到存放主题的目录 1、一般在入博客中的theme目录,这里以next主题为例。 在theme目录中,打开Git Bash Here; ls 列出主题目录 rm -rf 填需要删除的主题目录 2、另一种情况,以fluid主题为例;之前不知道是用那种…...

RK3399平台开发系列讲解(USB篇)U盘等存储类设备
🚀返回专栏总目录 文章目录 一、什么是U盘等存储类设备二、U盘设备传输数据结构三、U盘识别需要打开的宏沉淀、分享、成长,让自己和他人都能有所收获!😄 📢介绍U盘等存储类设备。 一、什么是U盘等存储类设备 USB Mass Storage Device Class(USB MSC/UMS) USB大容量存…...

一个页面需要加载大量的图片,如何提升用户体验?
当网站页面需要加载大量图片时,优化用户体验非常关键,以下是一些方法来提升用户体验: 图片懒加载(Lazy Loading):只加载用户可以看到的图片,当用户向下滚动页面时,再加载其他图片。这…...
JRT监听-PDF-Excel-Img
依赖全新设计,我们无需再顾虑历史兼容性的束缚;同时,基于多年来累积的深入需求理解,JRT监听机制巧妙地借助CMD命令模式,达成了监听的全面统一。无论是PDF、Excel还是图片文件,都不再需要特殊对待或额外区分…...
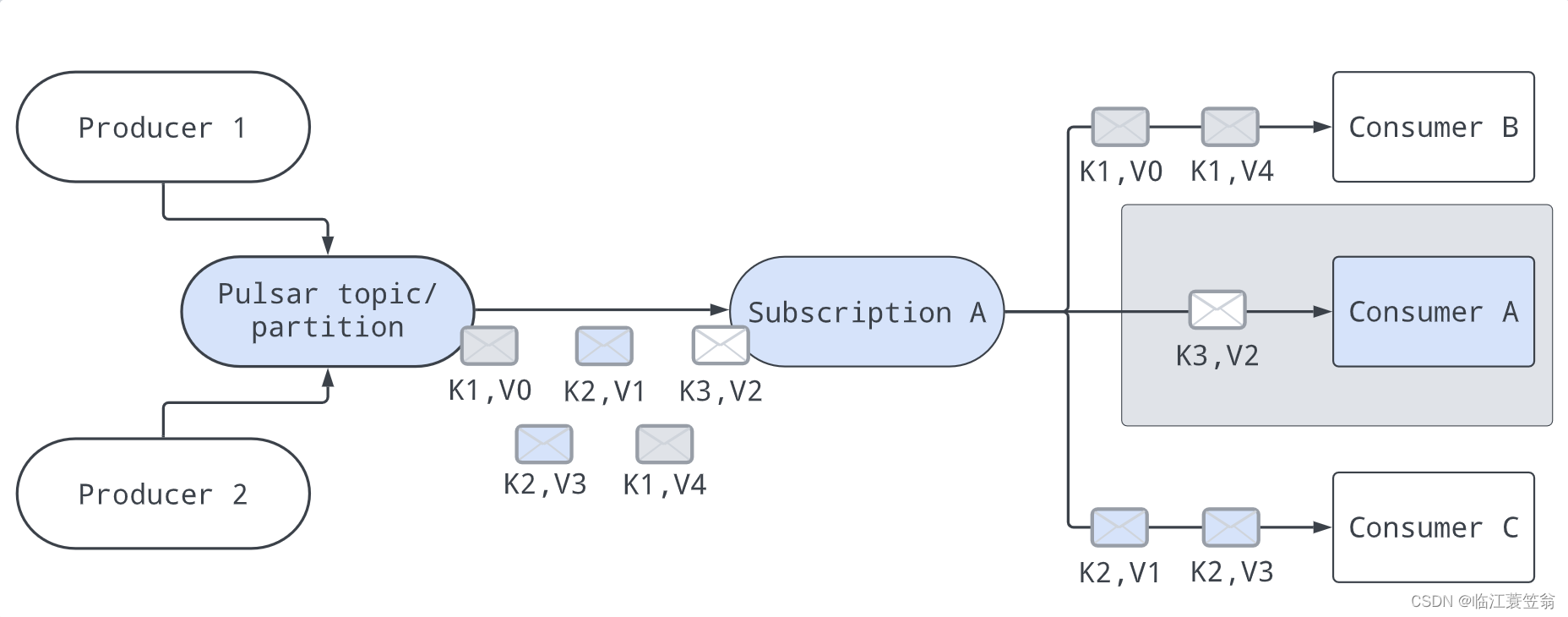
Pulsar-架构与设计
Pulsar架构与设计 一、背景和起源二、框架概述1.设计特点2.框架适用场景 三、架构图1.Broker2.持久化存储(Persistent storage)3.Pulsar元数据(Metadata store) 四、功能特性1.消息顺序性2.消息回溯3.消息去重4.消息重投递5.消息重…...

LeetCode每日一题589. N-ary Tree Preorder Traversal
文章目录 一、题目二、题解 一、题目 Given the root of an n-ary tree, return the preorder traversal of its nodes’ values. Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (S…...

html5移动端适配;检测浏览器信息函数
html5移动端适配 //动态改变font-size大小 (function changeFontSize() {let resizeEvt orientationchange in window ? orientationchange : resizeif (!isPC()) {let docEl document.documentElement;// recalc function () {let clientWidth docEl.clientWidth;docEl.…...

go依赖注入库samber/do使用
英语版本 介绍 以简单和高效而闻名的Go语言在其1.18版本中引入了泛型,这可以显着减少大量代码生成的需要,使该语言更加强大和灵活。如果您有兴趣, Go 泛型教程 是很好的学习资源。 通过使用 Go 的泛型,samber/do库为依赖注入 (…...
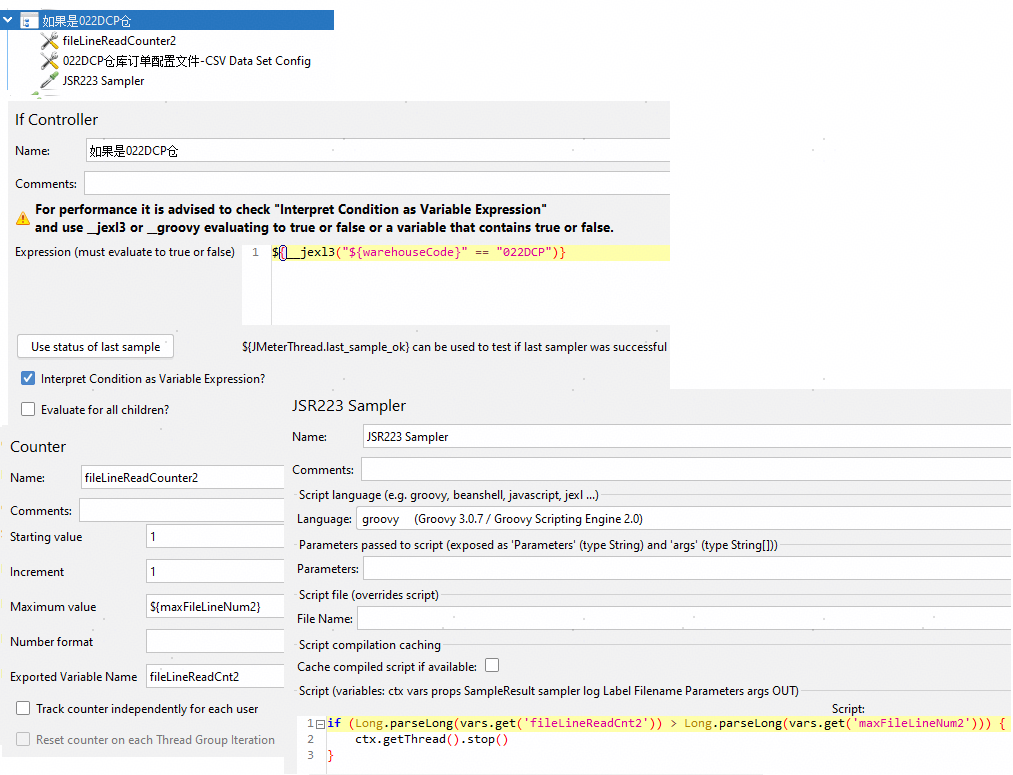
JMeter 配置元件之按条件读取CSV Data Set Config
实践环境 win10 JMeter 5.4.1 需求描述 需求是这样的,需要压测某个接口(取消分配接口),请求这个接口之前,需要先登录系统(物流WMS系统),并在登录后,选择并进入需要操作的仓库,然后请求接口,…...
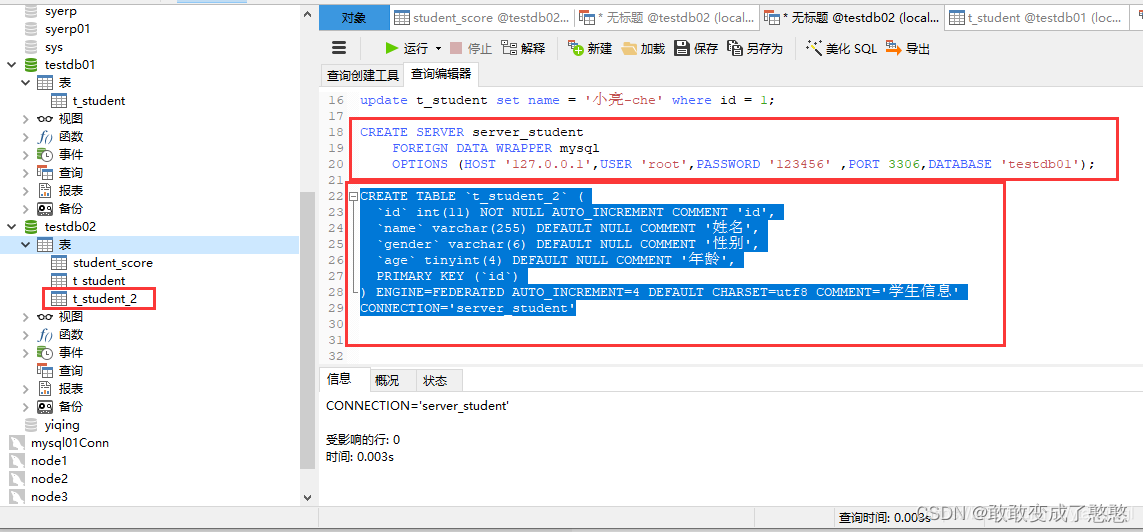
MySQL跨服务器关联查询
1. 首先确认服务器的Federated引擎是否开启 show engines;修改数据库的配制文件my.ini,(我的my.ini的路径为:D:\ProgramData\MySQL\MySQL Server 5.7/my.ini),将federated添加到my.ini文件中 到MySQL的my.cnf配置文件中修改 在 [mysqld] 下方加入 federated 然后重…...
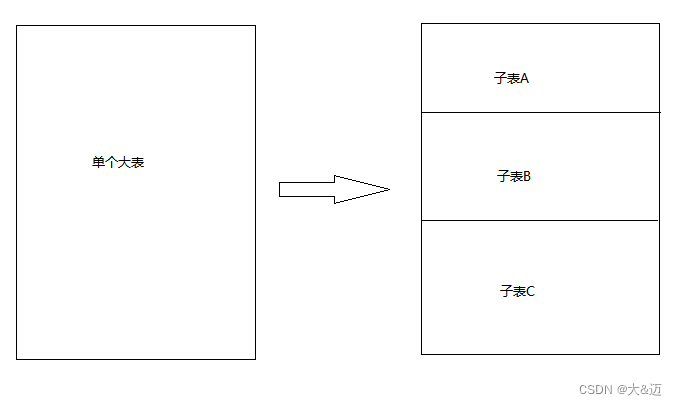
分库分表浅析
简介 对于任何系统而言,都会设计到数据库随着时间增长而累积越来越多的数据,系统也因为越来越多的需求变迁导致原有的设计不再满足现状,为了解决这些问题,分库分表就会走进视野,带着几个问题走入分库分表。 什么是分…...
java 宠物医院系统Myeclipse开发mysql数据库web结构jsp编程计算机网页项目
一、源码特点 java 宠物医院系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&…...
XMall 开源商城 SQL注入漏洞复现(CVE-2024-24112)
0x01 产品简介 XMall 开源电商商城 是开发者Exrick的一款基于SOA架构的分布式电商购物商城 前后端分离 前台商城:Vue全家桶 后台管理:Dubbo/SSM/Elasticsearch/Redis/MySQL/ActiveMQ/Shiro/Zookeeper等。 0x02 漏洞概述 XMall 开源商城 /item/list、/item/listSearch、/sys/…...
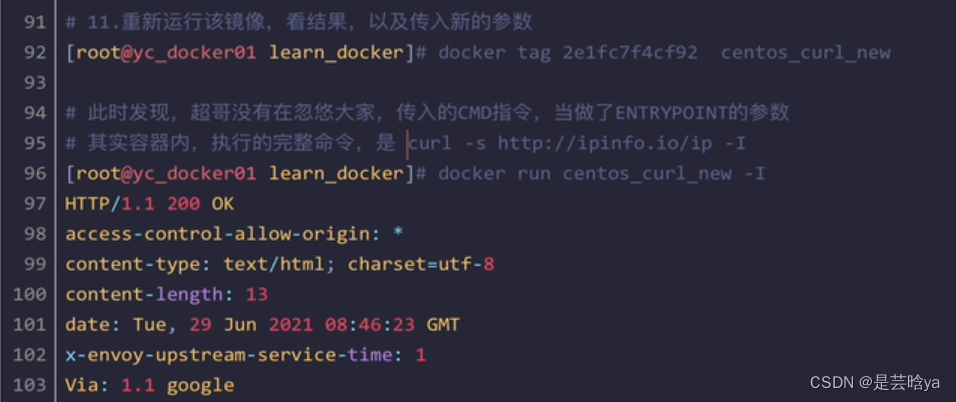
Docker原理及概念相关
Docker最核心的组件 image:镜像,构建容器,也可以通过Dockerfile文本描述镜像的内容。 (我们将应用程序运行所需的环境,打包为镜像文件) Container:容器 (你的应用程序,就跑在容器中 ) 镜像仓库(dockerhub)(…...

Vim相关配置
记录一下有关vim的一些设置,以免电脑寄了不好重新配置 vscodevim 首先是vscode中的vim模式 在应用商店中搜索vim插件安装即可 然后在setting中添加以下有关vim 的配置 "vim.easymotion": true,"vim.surround": true,"vim.incsearch"…...

ARMv8-AArch64 的异常处理模型详解之异常处理详解(进入异常以及异常路由)
在上篇文章 ARMv8-AArch64 的异常处理模型详解之异常处理概述Handling exceptions中,作者对异常处理整体流程以及相关概念做了梳理。接下来,本文将详细介绍处理器在获取异常、异常处理以及异常返回等过程中都做了哪些工作。 ARMv8-AArch64 的异常处理模型…...
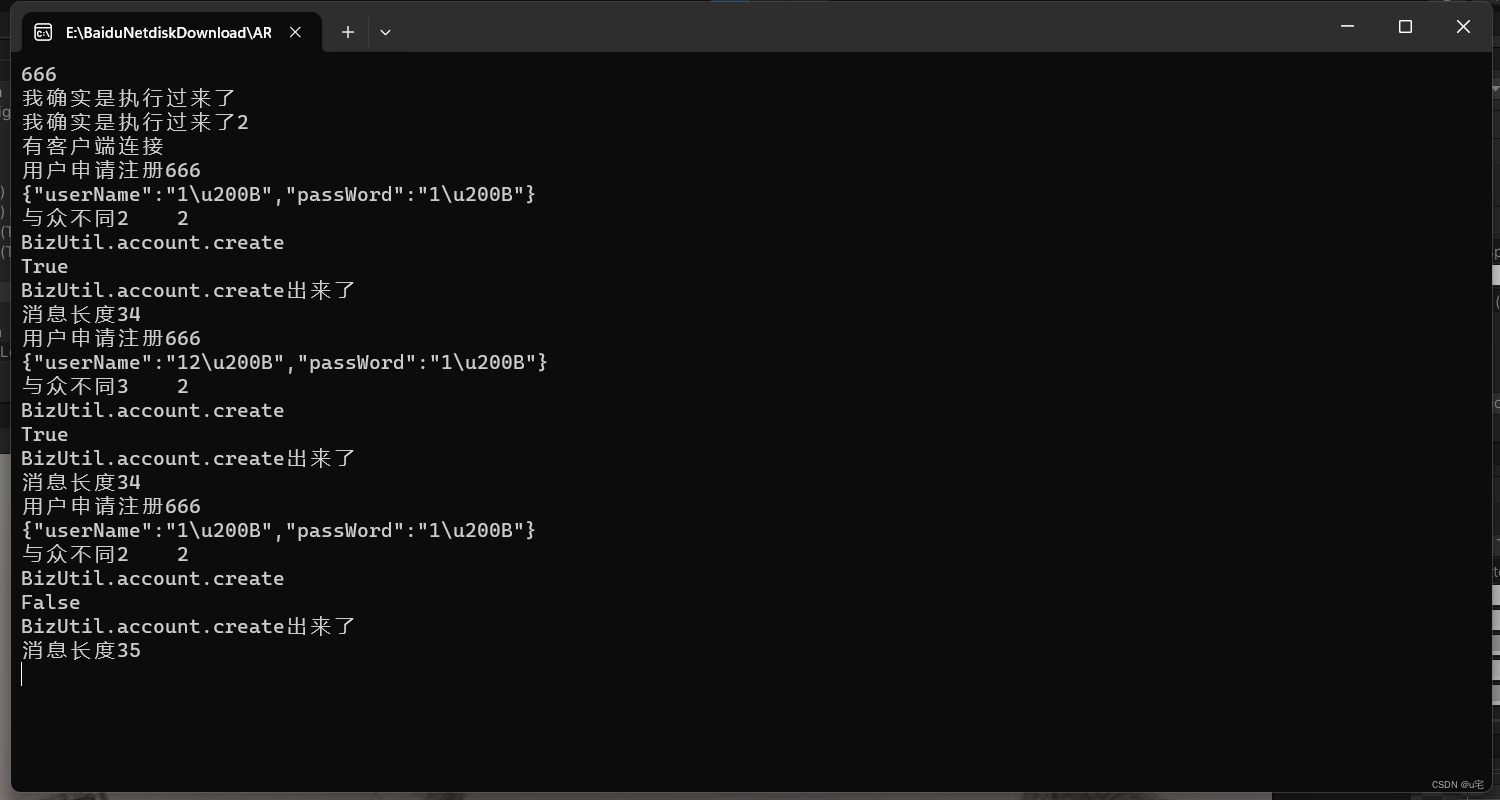
unity学习(19)——客户端与服务器合力完成注册功能(1)入门准备
逆向服务器用了三天的时间,但此时觉得一切都值,又可以继续学习了。 服务器中登录请求和注册请求由command变量进行区分,上一层的type变量都是login。 public void process(Session session, SocketModel model) {switch (model.Command){ca…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

