算法练习-01背包问题【含递推公式推导】(思路+流程图+代码)
难度参考
难度:困难
分类:动态规划
难度与分类由我所参与的培训课程提供,但需 要注意的是,难度与分类仅供参考。且所在课程未提供测试平台,故实现代码主要为自行测试的那种,以下内容均为个人笔记,旨在督促自己认真学习。
题目
动态规划经典问题01背包?
具体内容:
背包最大重量为4
物品如下:
| 重量 | 价值 | |
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的最大重量是多少?
思路
0-1 背包问题的动态规划解法基于以下思路:
-
子问题定义:
- 将原问题分解为子问题。在这里,我们考虑"对于给定的背包容量和一组物品,最大价值是多少?"
- 定义状态
dp[i][w]—— 表示考虑前i个物品时,对于不超过w重量的背包,所能得到的最大价值。
-
初始条件:
- 对于
dp[0][...],即一个物品也不考虑的情况,背包的价值总是 0。 - 对于
dp[...][0],即背包容量为 0 的情况,背包的价值也总是 0。
- 对于
-
递推关系(状态转移方程):
- 对于每一个物品
i和每一个可能的重量w,我们需要做出一个决策:是否将物品i放入背包。 - 如果不放物品
i,则dp[i][w] = dp[i-1][w]—— 也就是说,当前的最大价值与前i-1个物品时的最大价值相同。 - 如果放物品
i,我们必须确保当前背包的剩余容量至少是物品i的重量 (weights[i-1] <= w),在这种情况下,dp[i][w] = dp[i-1][w-weights[i-1]] + values[i-1]—— 也就是说,当前的最大价值是物品i的价值加上剩余重量在前i-1个物品中能得到的最大价值。
- 对于每一个物品
-
填表:
- 我们按照递推关系来填表 —— 从较小的
i和w开始,直到i等于物品个数,w等于背包最大重量。
- 我们按照递推关系来填表 —— 从较小的
-
解的构造:
- 表格填完后,
dp[n][maxWeight]就是答案 —— 即考虑所有物品和最大背包重量时的最大价值。
- 表格填完后,
补充-递推公式的推导:
假设我们有n个物品,每个物品的重量为weights[i],价值为values[i],背包的最大重量限制为maxWeight。我们定义dp[i][w]为考虑前i个物品(物品编号为0到i-1),在背包重量限制为w的情况下,能够得到的最大总价值。我们想求的最终答案是dp[n][maxWeight]。
对于每个物品i(从1开始计数,对应数组下标为i-1),以及每个可能的重量限制w,我们面临两种选择:
-
不包含当前物品:如果我们决定不包含当前考虑的物品
i-1,那么最大价值不会因为当前物品的存在而改变,所以它等于没有考虑当前物品时的最大价值,即dp[i-1][w]。 -
包含当前物品:如果我们决定包含当前考虑的物品
i-1,前提是这个物品的重量不超过当前的重量限制w(即weights[i-1] <= w)。此时,我们需要加上这个物品的价值values[i-1],同时,背包的剩余重量变为w - weights[i-1],因此我们还需要加上在新的重量限制下,考虑前i-1个物品时的最大价值,即dp[i-1][w-weights[i-1]] + values[i-1]。
因此,递推公式如下:
- 如果
weights[i-1] > w(当前物品重量超过背包限制),则dp[i][w] = dp[i-1][w]。 - 否则,
dp[i][w] = max(dp[i-1][w], dp[i-1][w-weights[i-1]] + values[i-1])。
这个递推公式基于以下逻辑:对于每个物品,我们都做出是否包含它的决定,以确保在不超过背包重量限制的情况下达到最大价值。这种方式确保了我们能够考虑所有可能的组合,并找到最优解。
示例
初始状态
首先,初始化一个表`dp`,其中`dp[i][j]`代表在只考虑前`i`个物品,且背包容量为`j`时的最大价值。初始化时,所有值均为0。
物品情况:
- 物品0:价值15,重量1
- 物品1:价值20,重量3
- 物品2:价值30,重量4
动态规划表格是这样的(行表示物品,列表示重量):
重量 0 1 2 3 4
不选物品 0 0 0 0 0加入物品0
加入物品0(价值15,重量1)后,我们更新表格。对于重量1及以上的列,我们可以加入物品0。
重量 0 1 2 3 4
不选物品 0 0 0 0 0
加入物品0 0 15 15 15 15加入物品1
接着,我们考虑加入物品1(价值20,重量3)。我们更新表格,考虑对于每个重量限制,在不超过该重量的情况下,是否加入物品1能获得更高的价值。
重量 0 1 2 3 4
不选物品 0 0 0 0 0
加入物品0 0 15 15 15 15
加入物品1 0 15 15 20 20在重量为4时,我们比较加入物品1后的价值与之前的状态。但是,我们忽略了一种可能:加入物品1(重量3,价值20)后,还可以再加入物品0(重量1,价值15),因此,对于重量4,最大价值应该是35(物品0和物品1的组合)。
加入物品2
最后,我们考虑加入物品2(价值30,重量4)。同样,我们更新表格,考虑对每个重量限制,加入物品2是否能带来更高的价值。
重量 0 1 2 3 4
不选物品 0 0 0 0 0
加入物品0 0 15 15 15 15
加入物品1 0 15 15 20 35
加入物品2 0 15 15 20 35在重量为4的情况下,加入物品2的价值(30)并不比已有的组合(物品0和物品1,总价值35)更优,因此我们保持原有的最大价值不变。
最终结果
最终,我们得到的动态规划表如下,表明在背包重量限制为4时,我们能获得的最大价值是35,通过组合物品0(价值15,重量1)和物品1(价值20,重量3)。
重量 0 1 2 3 4
不选物品 0 0 0 0 0
加入物品0 0 15 15 15 15
加入物品1 0 15 15 20 35
加入物品2 0 15 15 20 35因此,最终答案是,在确保总重量不超过4的条件下,我们最后得到的背包中的最大价值是35。
梳理
这个方法能够实现的原因在于它利用了动态规划(Dynamic Programming, DP)的两个关键性质:最优子结构和重叠子问题。
最优子结构意味着问题的最优解包含着其子问题的最优解。对于0-1背包问题来说,每增加一个物品的选择,都是基于之前所有物品选择的最优解上进行的新增决定。换句话说,在考虑是否加入当前物品时,我们可以依赖于之前物品的决策结果,这些决策结果是以最大化价值为目标的。
重叠子问题指的是在解决问题的过程中,相同的问题会被多次解决。在0-1背包问题中,当我们分别计算每一个重量限制下的最大价值时,会重复计算某些重量限制下的最大价值。通过动态规划,我们可以将这些价值存储在一个表中,避免重复计算,这就是为什么我们使用一个二维数组来存储每个子问题的答案。
在填充动态规划表时,我们从最小的子问题开始,即背包没有任何物品时的价值是0。然后逐步增加物品和重量,直到考虑了所有物品和所有重量限制。在每一步,针对每一个重量限制,我们都计算了两种情况:
1. 不加入当前的物品,直接使用之前同样重量限制下的最大价值。
2. 尝试加入当前的物品,将物品的价值加上剩余重量限制下的最大价值。
通过比较上述两种情况的价值,我们可以选择较大的一个作为当前重量限制和当前物品下的最大价值。这个过程一直持续到表格被填满,最终我们在表格的右下角得到的值就是我们能够拿到的最大价值。
简单来说,这方法之所以行之有效,是因为它将一个复杂问题分解为一系列叠加的简单问题并解决它们,同时保留了要求的全局最优解。通过表格的逐步填充,我们保证了在任何给定重量限制下,我们都是在做出最佳决策,以此计算出全局最优解。

代码
#include <iostream> // 引入标准输入输出库
#include <vector> // 引入向量(动态数组)库
using namespace std; // 使用标准命名空间,简化代码// 动态规划解决 0-1 背包问题的函数
int knapsack(const vector<int>& weights, const vector<int>& values, int maxWeight) {int n = weights.size(); // 物品数量// 初始化动态规划表,所有值起始为0vector<vector<int>> dp(n + 1, vector<int>(maxWeight + 1, 0)); // 使用动态规划构建 dp 数组for (int i = 1; i <= n; ++i) { // 遍历每个物品for (int w = 1; w <= maxWeight; ++w) { // 遍历每种重量限制// 如果当前物品可以加入背包if (weights[i - 1] <= w) {// 选择加入当前物品和不加入当前物品中价值更大的一个dp[i][w] = max(dp[i - 1][w], values[i - 1] + dp[i - 1][w - weights[i - 1]]);} else {// 如果不能加入当前物品,保持之前的最大价值dp[i][w] = dp[i - 1][w];}}}// 返回最大值,即考虑所有物品且不超过最大重量限制时的最大价值return dp[n][maxWeight];
}int main() {int maxWeight = 4; // 背包的最大重量限制vector<int> weights = {1, 3, 4}; // 物品的重量vector<int> values = {15, 20, 30}; // 物品的价值// 输出背包能达到的最大总价值cout << "背包能达到的最大总价值为 "<< knapsack(weights, values, maxWeight) << endl;return 0; // 程序正常结束
}时间复杂度:O(n * maxWeight)
空间复杂度:O(n * maxWeight)
打卡

相关文章:

算法练习-01背包问题【含递推公式推导】(思路+流程图+代码)
难度参考 难度:困难 分类:动态规划 难度与分类由我所参与的培训课程提供,但需 要注意的是,难度与分类仅供参考。且所在课程未提供测试平台,故实现代码主要为自行测试的那种,以下内容均为个人笔记࿰…...

Eclipse - Format Comment
Eclipse - Format & Comment 1. Correct Indentation2. Format3. Toggle Comment4. Add Block Comment5. Remove Block CommentReferences 1. Correct Indentation Ctrl A: 选择全部代码 Ctrl I: 校正缩进 or right-click -> Source -> Correct Indentation 2. F…...
mqtt 协议的概念和理解
一、概述 MQTT(Message Queuing Telemetry Transport,消息队列遥测传输协议),是一种基于发布/订阅(publish/subscribe)模式的”轻量级”通讯协议,该协议构建于TCP/IP协议上,由IBM在1…...

2024年大家都在用的AI写作软件推荐,写作不再是难题
人工智能(AI)已经渗透到我们生活的方方面面。在写作领域,AI写作软件已经成为越来越多人的首选工具。这些软件利用先进的自然语言处理技术和机器学习算法,能够帮助用户快速生成高质量的文章、论文、商业计划书等。在本文中…...

CPU是如何工作的?什么是冯·诺依曼架构和哈弗架构?
《嵌入式工程师自我修养/C语言》系列——CPU是如何工作的?什么是冯诺依曼架构和哈弗架构? 一、CPU内部结构及工作原理1.1 CPU的结构1.2 CPU工作流程举例 二、计算机体系结构2.1 冯诺依曼架构2.2 哈弗架构 三、总结 快速学习嵌入式开发其他基础知识&#…...

OpenAI视频生成模型Sora的全面解析:从扩散Transformer到ViViT、DiT、NaViT、VideoPoet
前言 真没想到,距离视频生成上一轮的集中爆发(详见《视频生成发展史:从Gen2、Emu Video到PixelDance、SVD、Pika 1.0、W.A.L.T》)才过去三个月,没想OpenAI一出手,该领域又直接变天了 自打2.16日OpenAI发布sora以来(其开发团队包…...

【Java】图解 JVM 垃圾回收(一):GC 判断策略、引用类型、垃圾回收算法
图解 JVM 垃圾回收(一) 1.前言1.1 什么是垃圾1.2 内存溢出和内存泄漏 2.垃圾回收的定义与重要性3.GC 判断策略3.1 引用计数算法3.2 可达性分析算法 4.引用类型5.垃圾回收算法5.1 标记-复制(Copying)5.2 标记-清除(Mark…...

做抖店需要注意的几大点,新手最易踩坑,都给你们总结到这了!
我是电商珠珠 抖店的运营流程很简单,选品上架、获取流量(找达人、自播、投千川等)、出单发货、做体验分等。出新手期就会有体验分,体验分就是店铺的权重,体验分越高店铺的权重也就越大。 但是作为新手的话࿰…...
)
小程序API能力汇总——基础容器API(三)
ty.getAccountInfo 获取小程序账号信息 需引入MiniKit,且在>3.1.0版本才可使用 参数 Object object 属性类型默认值必填说明completefunction否接口调用结束的回调函数(调用成功、失败都会执行)successfunction否接口调用成功的回调函数…...

处理目标检测中的类别不均衡问题
目标检测中,数据集中类别不均衡是一个常见的问题,其中一些类别的样本数量明显多于其他类别。这可能导致模型在训练和预测过程中对频繁出现的类别偏向,而忽略掉罕见的类别。本文将介绍如何处理目标检测中的类别不均衡问题,以提高模…...
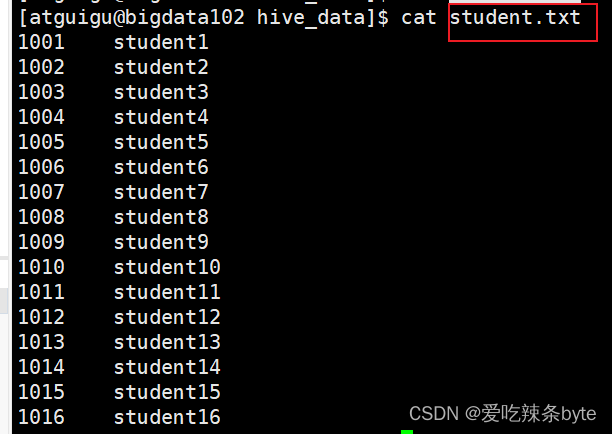
(03)Hive的相关概念——分区表、分桶表
目录 一、Hive分区表 1.1 分区表的概念 1.2 分区表的创建 1.3 分区表数据加载及查询 1.3.1 静态分区 1.3.2 动态分区 1.4 分区表的本质及使用 1.5 分区表的注意事项 1.6 多重分区表 二、Hive分桶表 2.1 分桶表的概念 2.2 分桶表的创建 2.3 分桶表的数据加载 2.4 …...

2024年首发!高级界面控件Kendo UI全新发布2024 Q1
Kendo UI是带有jQuery、Angular、React和Vue库的JavaScript UI组件的最终集合,无论选择哪种JavaScript框架,都可以快速构建高性能响应式Web应用程序。通过可自定义的UI组件,Kendo UI可以创建数据丰富的桌面、平板和移动Web应用程序。通过响应…...

stable diffusion webui学习总结(2):技巧汇总
一、脸部修复:解决在低分辨率下,脸部生成异常的问题 勾选ADetailer,会在生成图片后,用更高的分辨率,对于脸部重新生成一遍 二、高清放大:低分辨率照片提升到高分辨率,并丰富内容细节 1、先通过…...
java 培训班预定管理系统Myeclipse开发mysql数据库web结构jsp编程servlet计算机网页项目
一、源码特点 java 培训班预定管理系统是一套完善的java web信息管理系统 采用serlvetdaobean,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为TOMCAT7.0,Myeclipse8.5开发…...

Python内置函数06——join
文章目录 概述语法实例展示注意事项 概述 Python内置函数join()用于将序列中的元素连接成一个字符串。 语法 str.join(iterable) 参数:iterable——一个可迭代对象中元素连接而成,元素之间用str分隔。 实例展示 eg1:用join()连接列表中…...

linux安装单机版redis详细步骤,及python连接redis案例
文章目录 linux相关工具yum方式安装redis使用编译安装redis配置redis为systemctl启动其它: 安装redis6.0python连接redis案例 linux相关工具 ./redis-benchmark #用于进行redis性能测试的工具 ./redis-check-dump #用于修复出问题的dump.rdb文件 ./redis-cli …...

ts总结大全
ts类型 TS类型除了原始js类型之外,还增加类型,例如:枚举、接口、泛型、字面量、自定义、类型断言、any、类型声明文件 数组类型两种写法:类型 [] 或 Array <类型> let arr:number[][1,2,3,4] let arr:string[][a] let arr…...
前端登录随机数字字母组合验证
背景:系统登录页面只有用户名密码一种校验方式,没有验证码,可能导致暴力破解。 实现逻辑: <el-form-item prop="code"><el-inputv-model="loginForm.captchaCode"auto-complete="off"placeholder="验证码"style="wi…...

基于Java+SpringBoot+vue+elementui 实现即时通讯管理系统
目录 系统简介效果图源码结构试用地址源码下载地址技术交流 博主介绍: 计算机科班人,全栈工程师,掌握C、C#、Java、Python、Android等主流编程语言,同时也熟练掌握mysql、oracle、sqlserver等主流数据库,能够为大家提供…...
 ● 322. 零钱兑换 ● 279.完全平方数)
代码随想录算法训练营第50天(动态规划07 ● 70. 爬楼梯 (进阶) ● 322. 零钱兑换 ● 279.完全平方数
动态规划part07 70. 爬楼梯 (进阶)解题思路总结 322. 零钱兑换解题思路总结 279.完全平方数解题思路 70. 爬楼梯 (进阶) 这道题目 爬楼梯之前我们做过,这次再用完全背包的思路来分析一遍 文章讲解: 70. 爬…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
