由斐波那契数列探究递推与递归
斐波那契数列定义:
斐波那契数列大家都非常熟悉。它的定义是:
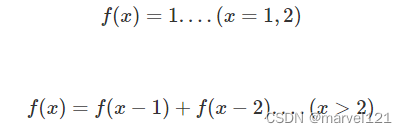
对于给定的整数 x ,我们希望求出: f ( 1 ) + f ( 2 ) + … + f ( x ) f(1)+f(2)+…+f(x) f(1)+f(2)+…+f(x) 的值。
有两种方法,分别是递推(迭代)与递归
具体解释如下图
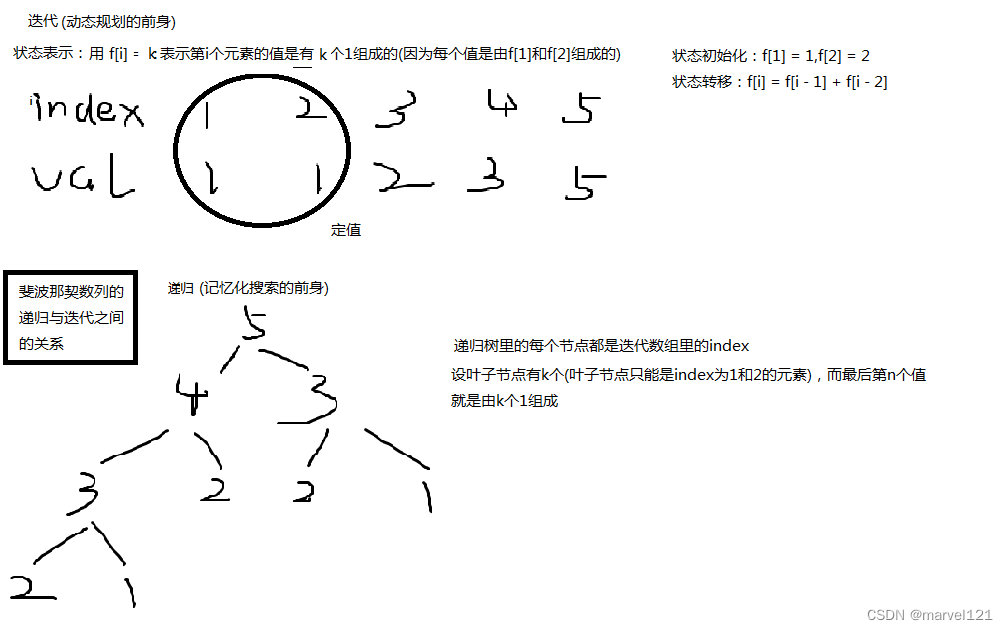
备注:递推(迭代)的方式是利用开一个有 x 个元素的数组,表示由 x 种的状态,本质上是利用空间换时间,然后循环迭代每一个状态,其中一个新状态是由两个旧状态递推出来的,整个递推过程只需要 O ( n ) O(n) O(n) 的时间复杂度,所以此种方法运行的时间复杂度要低于递归的方法。
递归的方法更像是一种暴搜(暴力搜索每一种状态),所有搜索到的状态构成一颗递归搜索树,搜索的次数就是所有树上的节点的个数,可以看到递归搜索树的节点树远大于循环迭代次数,其时间复杂度大约为 O ( 2 n − 2 ) O(2^{n - 2}) O(2n−2) 。
代码:
方法一:递推(迭代)
时间复杂度 O ( n ) O(n) O(n)
typedef long long ll;
const int N = 70;ll fib_dp(int x) //递推
{vector<ll> dp(N,0);dp[0] = 0,dp[1] = 1;for (int i = 2;i <= x;i ++ ) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[x];
}
方法二:递归
时间复杂度 O ( 2 n − 2 ) O(2^{n - 2}) O(2n−2)
typedef long long ll;
const int N = 70;ll fib_recursion(int x) //递归
{if (!x) return 0;else if (x == 1 || x == 2) return 1;else {return fib_recursion(x - 1) + fib_recursion(x - 2); //后序遍历的写法}
}
相关文章:

由斐波那契数列探究递推与递归
斐波那契数列定义: 斐波那契数列大家都非常熟悉。它的定义是: 对于给定的整数 x ,我们希望求出: f ( 1 ) f ( 2 ) … f ( x ) f(1)f(2)…f(x) f(1)f(2)…f(x) 的值。 有两种方法,分别是递推(迭代)与递归 具体解释如下图 备注…...

红队打靶练习:IMF: 1
目录 信息收集 1、arp 2、nmap 3、nikto 目录探测 gobuster dirsearch WEB 信息收集 get flag1 get flag2 get flag3 SQL注入 漏洞探测 脱库 get flag4 文件上传 反弹shell 提权 get flag5 get flag6 信息收集 1、arp ┌──(root㉿ru)-[~/kali] └─# a…...
?)
密码管理局以及什么是密评?为什么要做密评(商用密码应用安全性评估)?
文章目录 密码管理局以及什么是密评?为什么要做密评?关于密码管理局国家密码管理局属于什么级别?什么是密评?密评发展史为什么要做密评?目前密码应用的几个问题密评对象不做“密评”或密评不合格有什么影响?如何才能顺利通过密评?密评的相关标准参考密码管理局以及什么是…...
六、Datax通过json字符串运行
Datax通过json字符串运行 一、场景二、代码实现 一、场景 制作一个web应用,在页面上配置一个json字符串,保存在数据库里面。在执行json的时候,动态在本地创建一个json文件后执行,并识别是否成功,将执行过程保存在数据…...

关于数据库
目录 一 什么是数据库(DB) 二 什么是数据库管理系统(DBMS) 三 数据库的作用/好处 一 什么是数据库(DB) 简单理解,数据库是存放数据的地方,就像冰箱是存放冷鲜食品的地方。 数据是数据存储的基本对象,而数据分为多…...
洛谷C++简单题小练习day14—闰年推算小程序
day14--闰年推算小程序--2.18 习题概述 题目描述 输入 x,y,输出 [x,y] 区间中闰年个数,并在下一行输出所有闰年年份数字,使用空格隔开。 输入格式 输入两个正整数 x,y,以空格隔开。 输出格式 第一行输出一个正整数…...
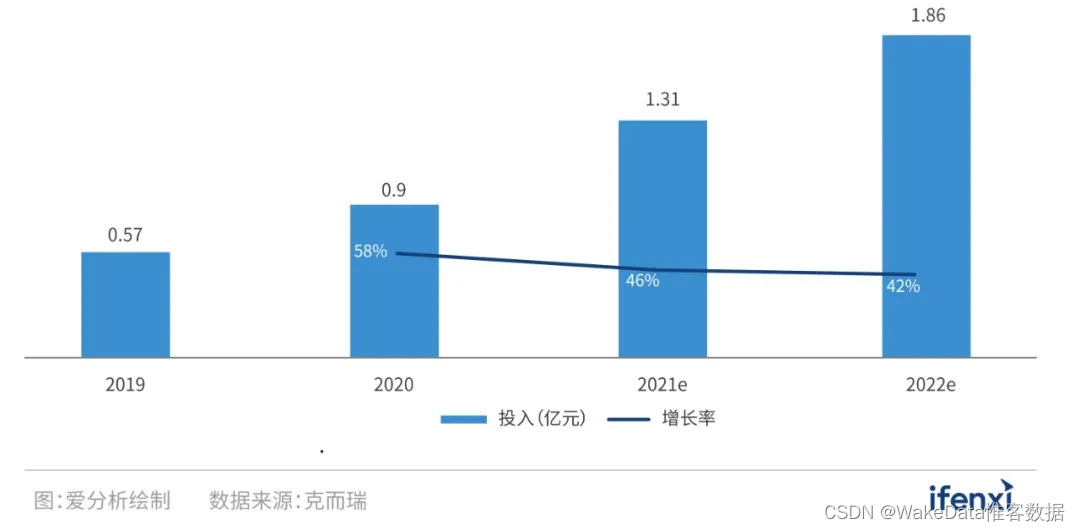
房企关注的典型数字化场景之一:数字营销
过去在增量时代下,房企的模式是“拿地-开发-卖房-拿地”,谁拿的地多、卖得快、利润高,谁“活得好”。而进入存量时代,加上政策调控影响,房企需要将核心竞争力转向精细化、多元化运营。 根据克而瑞数据统计,…...
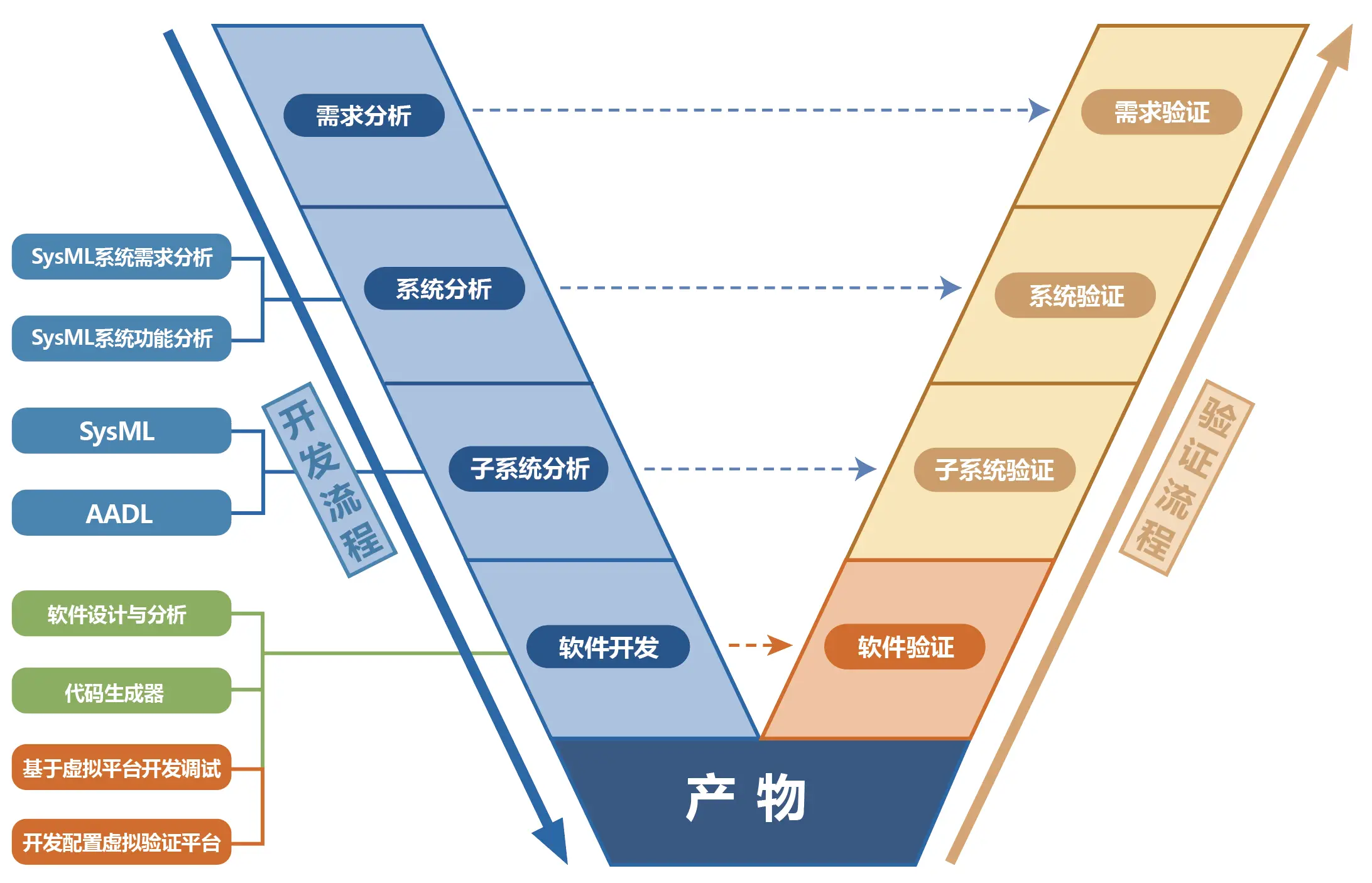
BMS再进阶(新能源汽车电池管理系统)
引言 一文入门BMS(电池管理系统)_bms电池管理-CSDN博客 BMS进阶(Type-C、PD快充、充电IC、SOC算法、电池管理IC)_充电ic asi aso功能-CSDN博客 本文是上面两篇博客的续篇,之前都是讲解一些BMS基本原理,…...

K8s Deployment挂载ConfigMap权限设置
目录 样例 1. 样例 …… volumes: - configMap:defaultMode: 420name: ${Existed_configmap_name} …… 其中“defaultMode: 420”是设置权限的 2. 解析 在K8s(Kubernetes)中,defaultMode是用来设置Configmap挂载后的文件权限࿰…...

百度智能云分布式数据库 GaiaDB-X 与龙芯平台完成兼容认证
近日,百度智能云的分布式关系型数据库软件 V3.0 与龙芯中科技术股份有限公司的龙芯 3C5000L/3C5000 处理器平台完成兼容性测试,功能与稳定性良好,获得了龙架构兼容互认证证书。 龙芯系列处理器 通用 CPU 处理器是信息产业的基础部件…...
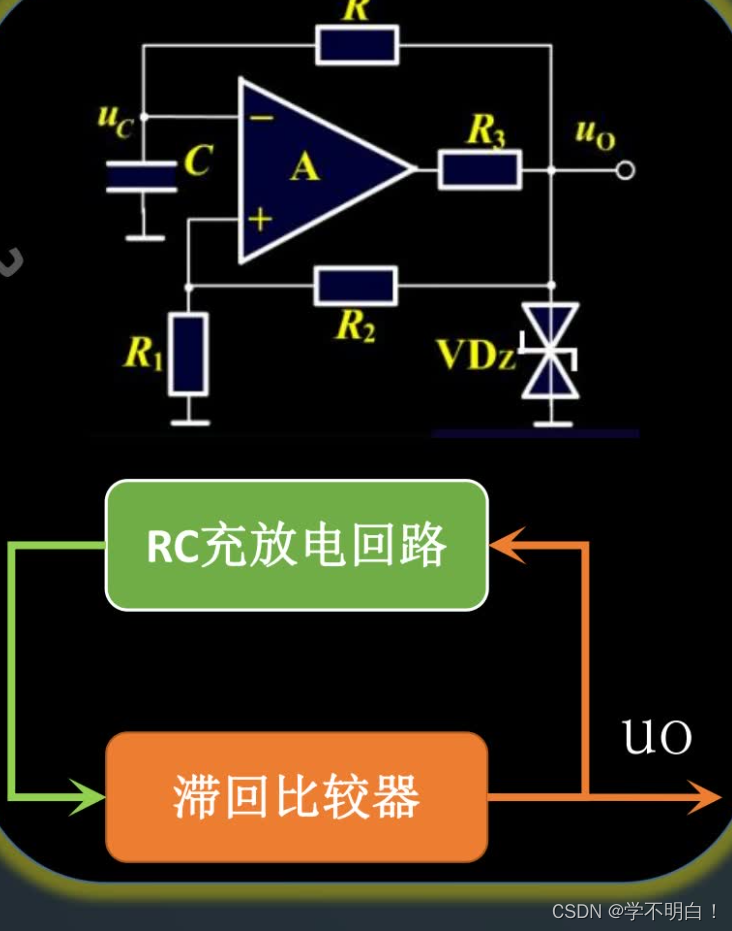
模拟电子技术——振荡器基本原理、RC桥式振荡器、矩形波发生电器
文章目录 前言一、振荡器什么是振荡器振荡器的基本电路结构振荡条件起振条件和稳幅原理 二、RC桥式振荡器什么是RC桥式振荡器RC串并联网络的选频特性振荡条件完整频率特性曲线举例 三、矩形波发生电器什么是矩形波发生电路稳态与暂态PWM脉宽调制矩形波发生电路基本组成 总结 前…...
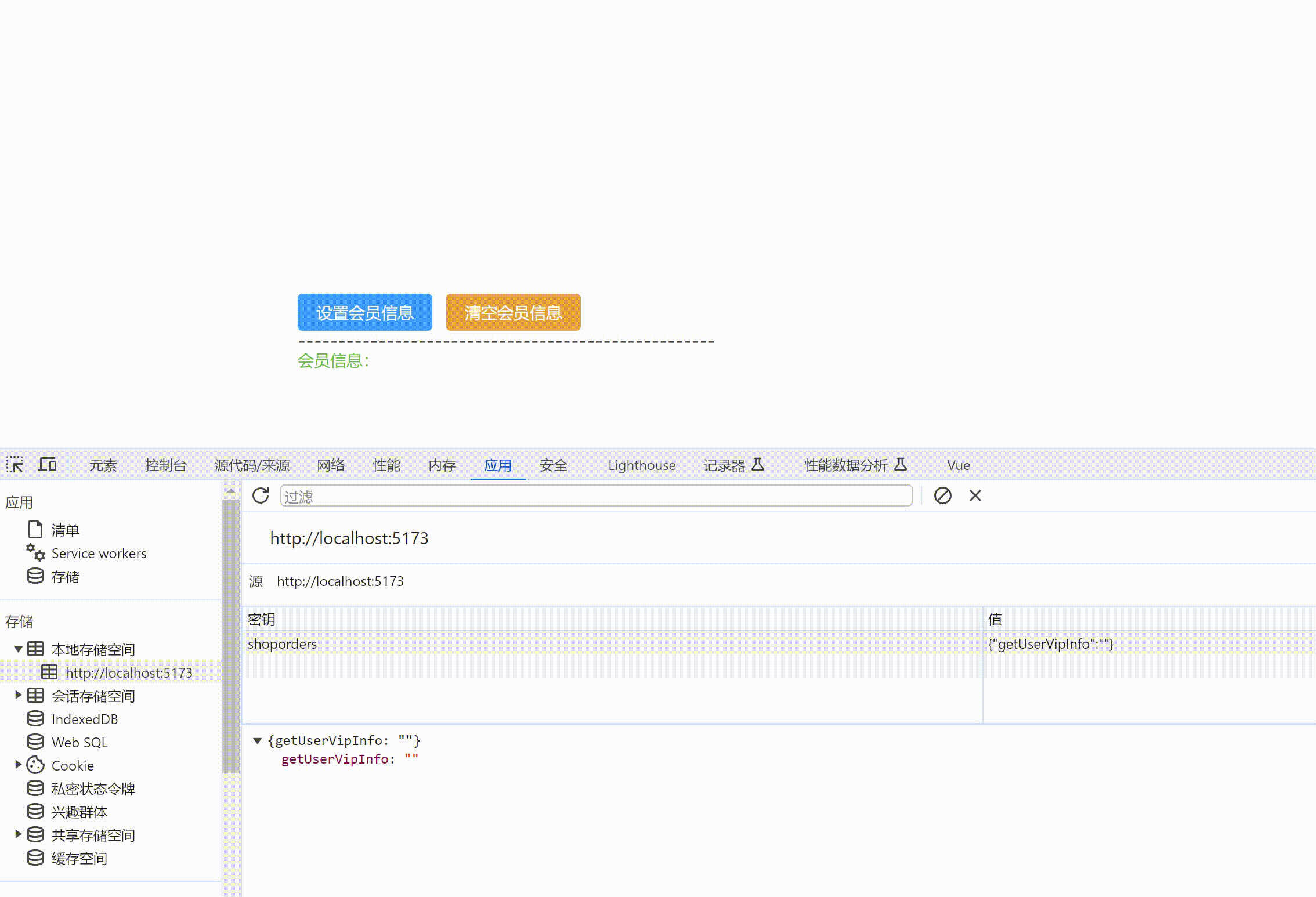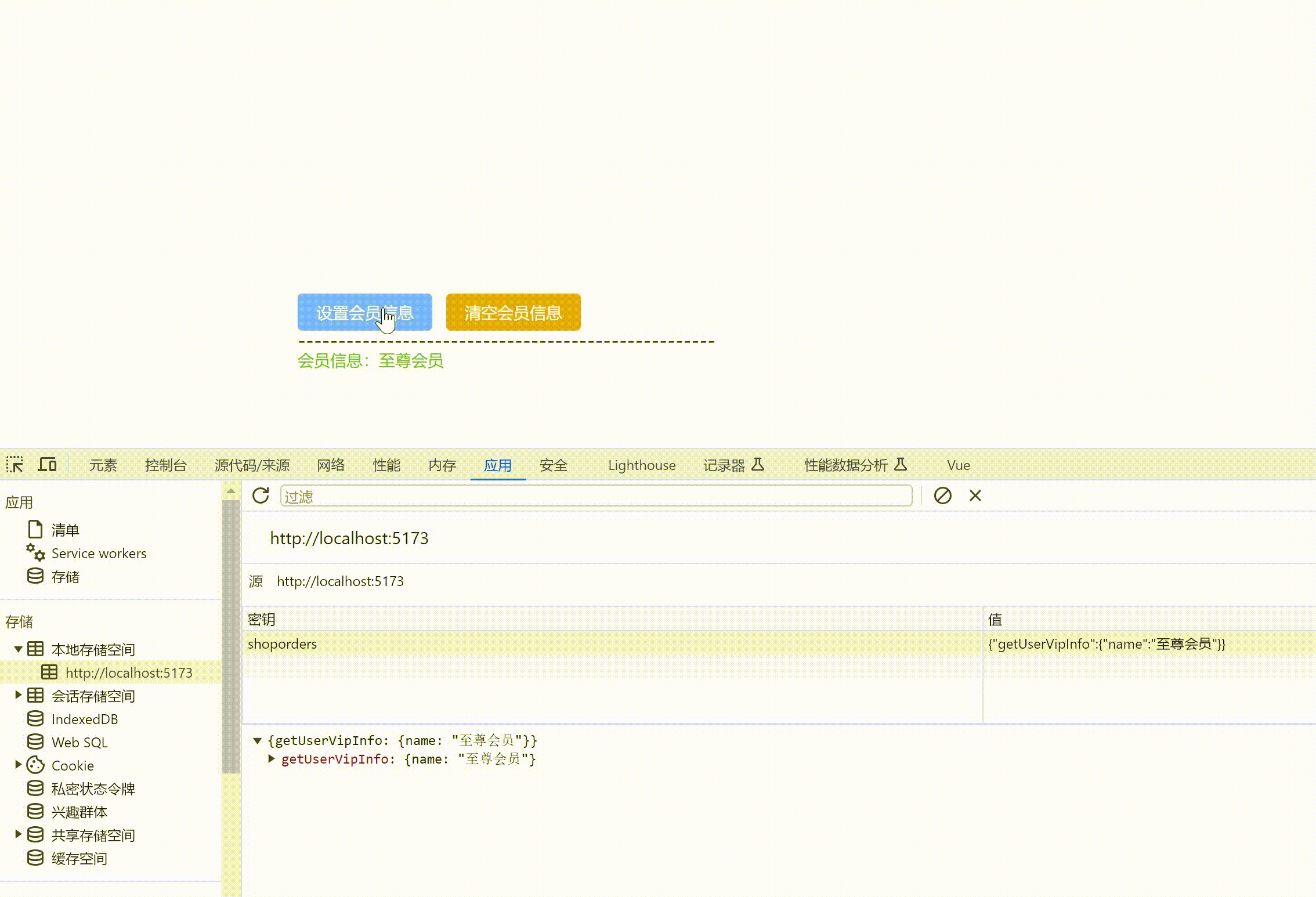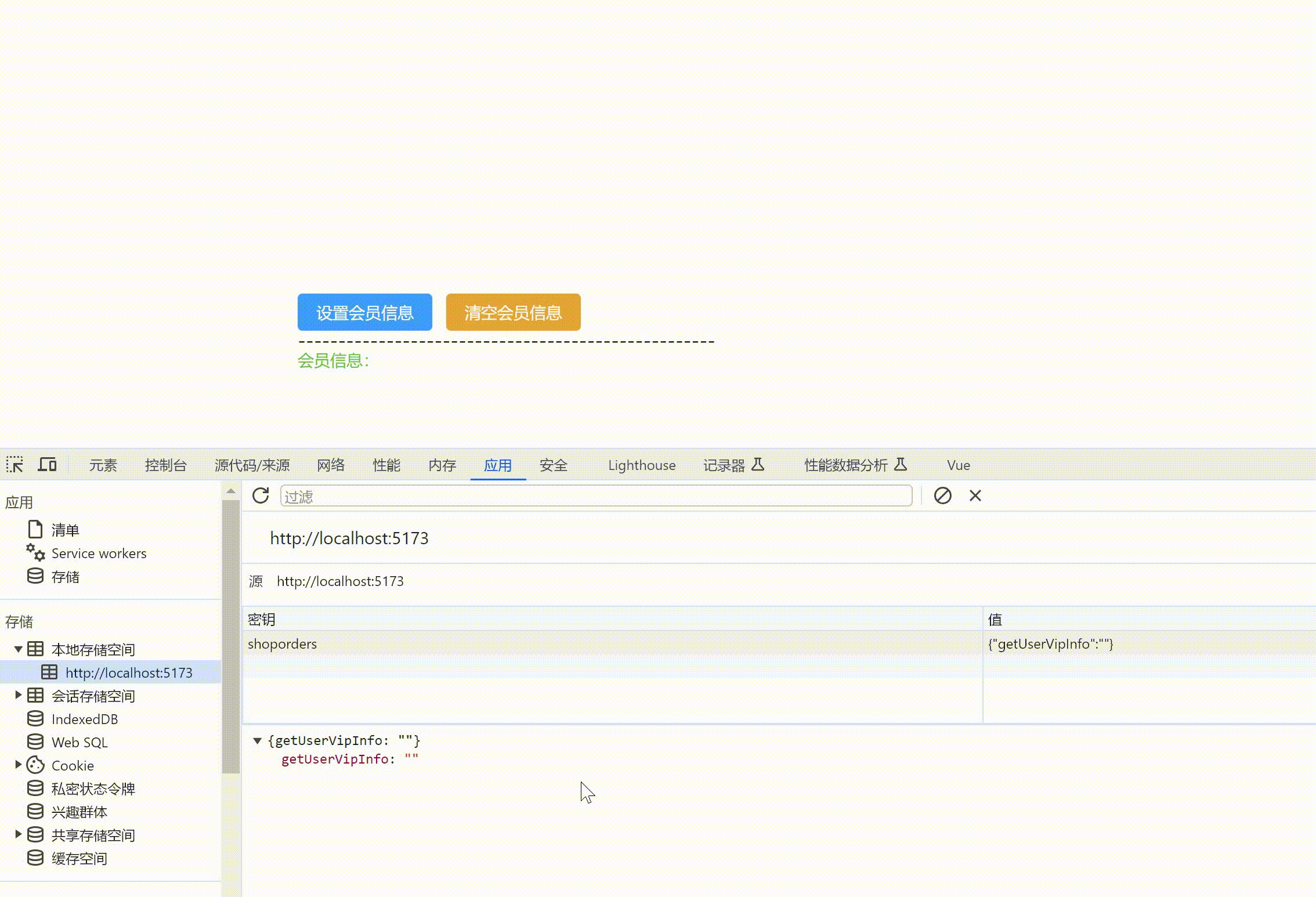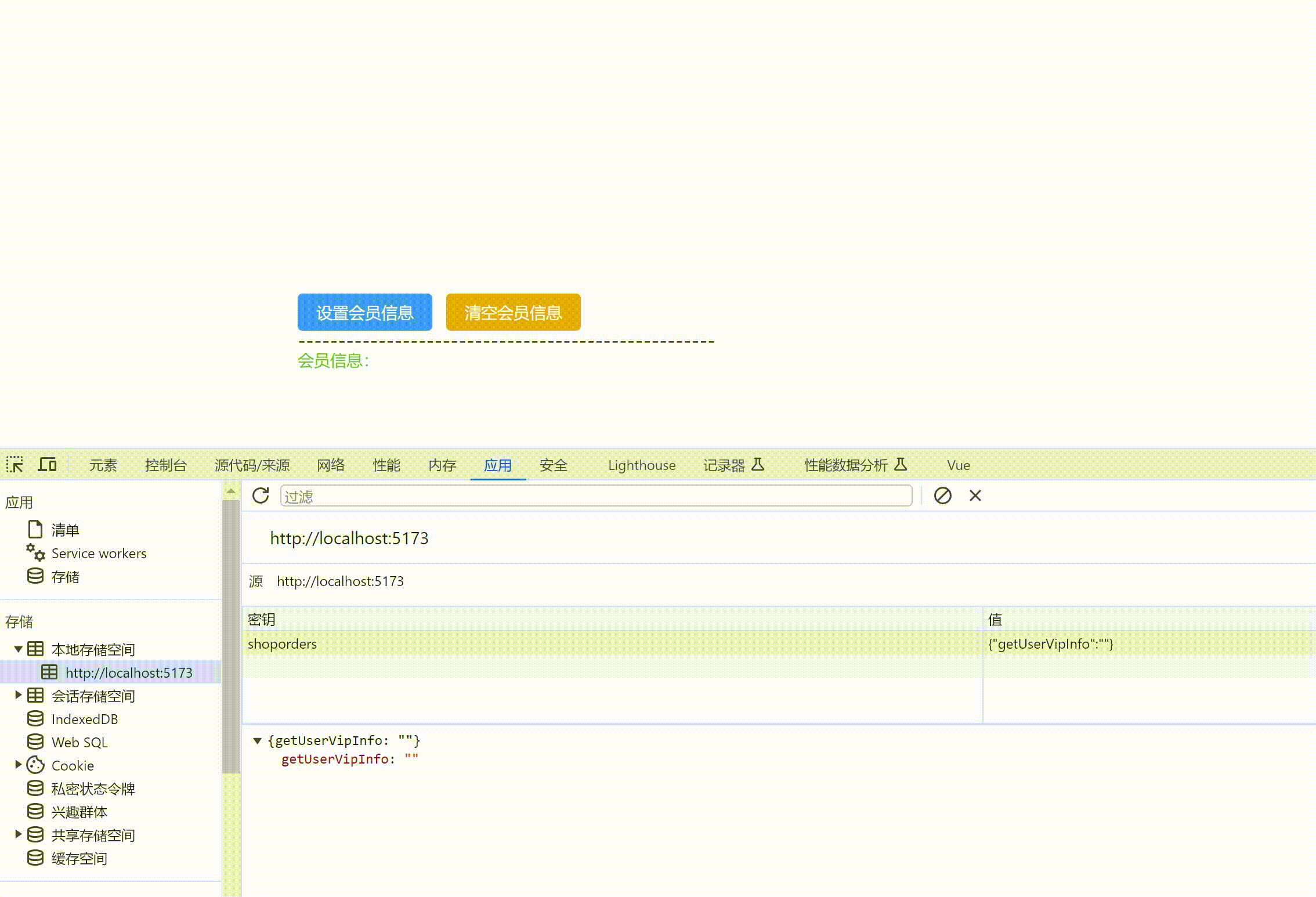
Vue3+Vite+TS+Pinia+ElementPlus+Router+Axios创建项目
目录 初始项目组成1. 创建项目1.1 下载项目依赖1.2 项目自动启动1.3 src 别名设置vite.config.ts配置文件tsconfig.json配置若新创项目ts提示 1.4 运行测试 2. 清除默认样式2.1 样式清除代码下载2.2 src下创建公共样式文件夹style2.3 main.js中引入样式2.4 安装sass解析插件 2.…...

VMware虚拟机安装CentOS7
对于系统开发来说,开发者时常会需要涉及到不同的操作系统,比如Windows系统、Mac系统、Linux系统、Chrome OS系统、UNIX操作系统等。由于在同一台计算机上安装多个系统会占据我们大量的存储空间,所以虚拟机概念应运而生。本篇将介绍如何下载安…...
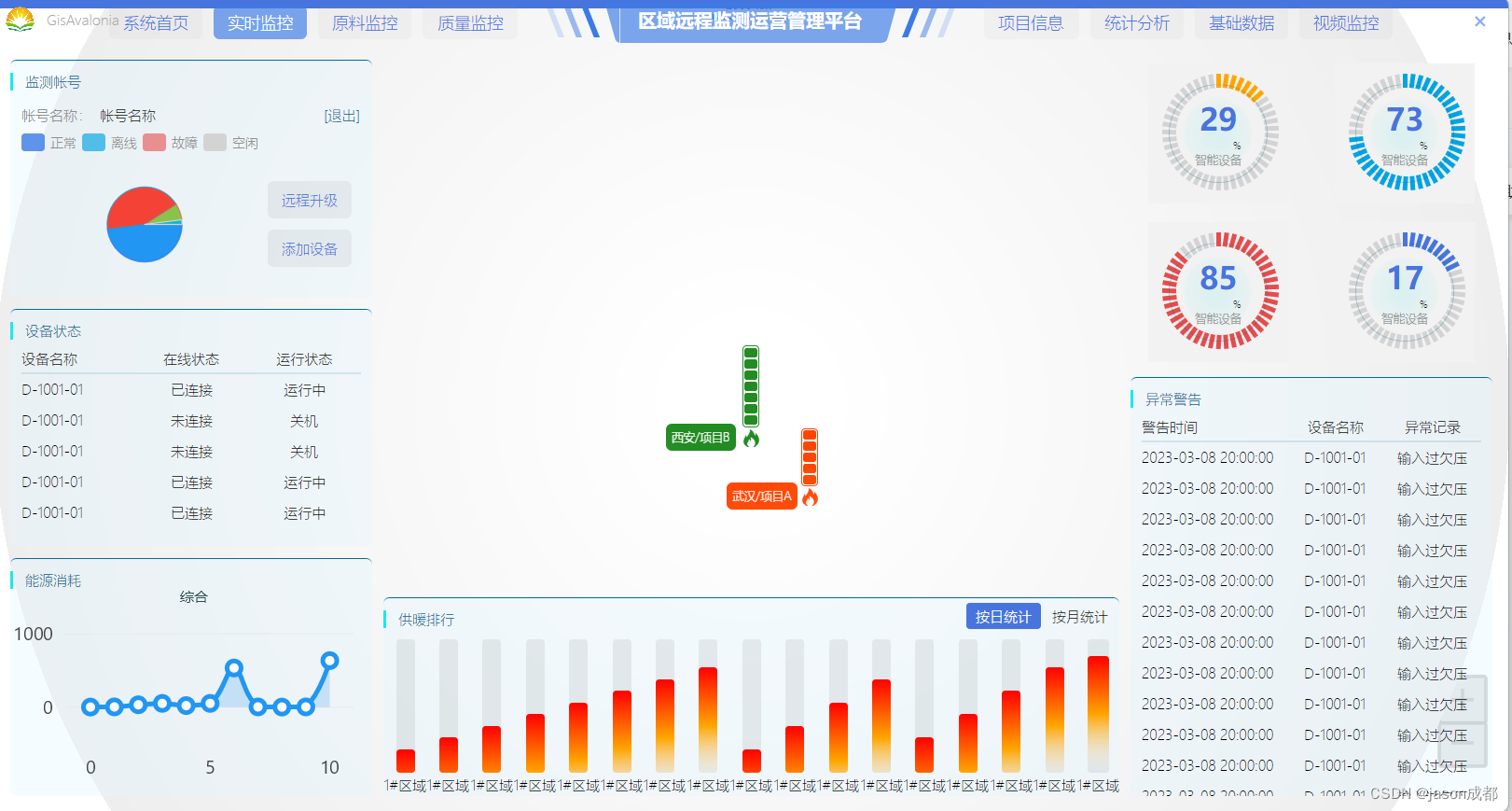
Avalonia学习(二十四)-系统界面
目前项目式练习,界面内容偏多,所以不给大家贴代码了,可以留言交流。此次为大家展示的是物联项目的例子,仅仅是学习,我把一些重点列举一下。 界面无边框 以前的样例主要是通过实现控件来完成的,前面已经有窗…...

深入解析鸿蒙系统的页面路由(Router)机制
鸿蒙系统以其独特的分布式架构和跨设备的统一体验而备受瞩目。在这个系统中,页面路由(Router)机制是连接应用各页面的关键组成部分。本文将深入探讨鸿蒙系统的页面路由,揭示其工作原理、特点以及在应用开发中的实际应用。 1. 实现…...

MCU中断响应流程及注意事项
本文介绍MCU中断响应流程及注意事项。 1.中断响应流程 中断响应的一般流程为: 1)断点保护 硬件操作,将PC,PSR等相关寄存器入栈保护 2)识别中断源 硬件操作,识别中断的来源,如果多个中断同时发生,高优…...
基于Java SSM框架实现网上报名系统项目【项目源码+论文说明】计算机毕业设计
基于java的SSM框架实现网上报名系统演示 摘要 随着互联网时代的到来,同时计算机网络技术高速发展,网络管理运用也变得越来越广泛。因此,建立一个B/S结构的网上报名系统,会使网上报名系统工作系统化、规范化,也会提高网…...

Eclipse - Formatter
Eclipse - Formatter References Window -> Preferences -> C/C -> Code Style -> Formatter BSD/Allman [built-in] or K& R [built-in] References [1] Yongqiang Cheng, https://yongqiang.blog.csdn.net/...

算法练习-01背包问题【含递推公式推导】(思路+流程图+代码)
难度参考 难度:困难 分类:动态规划 难度与分类由我所参与的培训课程提供,但需 要注意的是,难度与分类仅供参考。且所在课程未提供测试平台,故实现代码主要为自行测试的那种,以下内容均为个人笔记࿰…...

Eclipse - Format Comment
Eclipse - Format & Comment 1. Correct Indentation2. Format3. Toggle Comment4. Add Block Comment5. Remove Block CommentReferences 1. Correct Indentation Ctrl A: 选择全部代码 Ctrl I: 校正缩进 or right-click -> Source -> Correct Indentation 2. F…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...
