DS:八大排序之归并排序、计数排序
创作不易,感谢三连支持!!
一、归并排序
1.1 思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。

还有一个关键点就是:归并一定要先拷贝到一个新数组里面,再拷贝到原数组!!
1.2 递归实现归并排序
根据上面的思路,我们来实现代码:
void _MergeSort(int* a, int begin, int end, int* temp)
{if (begin == end)return;//设置递归返回条件int mid = (begin + end) / 2;//开始分解_MergeSort(a, begin, mid, temp);//左区间归并_MergeSort(a, mid+1, end, temp);//右区间归并//开始进行总归并int begin1 = begin, end1 = mid;//设置指针指向左区间int begin2 = mid + 1, end2 = end;//设置指针指向右区间int i = begin;//用来遍历拷贝数组while (begin1 <= end1 && begin2 <= end2)//只要有一个先拷贝完,就跳出循环{//谁小谁尾插if (a[begin1] < a[begin2])temp[i++] = a[begin1++];elsetemp[i++] = a[begin2++];}//这个时候其中一个区间先遍历完了,这个时候另一个没有遍历的区间插入就可以了//以下两个while只会执行一个while (begin1 <= end1)temp[i++] = a[begin1++];while (begin2<=end2)temp[i++] = a[begin2++];//归并完成,将temp的数据拷贝回去memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));//因为递归,拷贝的不一定就是从头开始的,左闭右闭个数要+1;
}
void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功,开始进行递归_MergeSort(a, 0, n - 1, temp);
}要注意:递归的返回条件是begin==end!!因此归并排序每次拆分都是从中间拆分的,所以不可能会出现区间不存在的情况!! 只有可能是区间只有一个元素的情况
1.3 非递归实现归并排序
怎么去思考非递归实现归并排序呢??我们来画图理解:

那我们其实可以通过指针来实现各个子区间的有序,直接在原数组上建立两个指针
我们设置一个gap来分割区间

这里的问题就是,如何控制每次归并的子序列的范围?以及什么时候结束归并?
一、gap 控制几个为一组归并(gap一开始从1开始),则:
第一个子序列的起始是begin1 = i, end1 = i + gap -1;
第二个子序列的起始是begin2 = i+gap, end2 = i + 2 *gap - 1;
其中i是遍历一遍待排序的数组的下标,i从0开始。i每次应该跳2*gap步。
二、gap控制的是每次几个为一组我们 一开始是1个,2个、4个、8个,显然是2的倍数,所以gap每次乘等2即可!也不能一直让gap*=2下去,gap不可能大于等于数组的长度,所以当超过数组的长度是结束!
代码实现:
void MergeSortNonR(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功int gap = 1;while (gap < n){int j = 0;//用来遍历拷贝数组for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;while (begin1 <= end1 && begin2 <= end2)//只要有一个先拷贝完,就跳出循环{//谁小谁尾插if (a[begin1] < a[begin2])temp[j++] = a[begin1++];elsetemp[j++] = a[begin2++];}//这个时候其中一个区间先遍历完了,这个时候另一个没有遍历的区间插入就可以了//以下两个while只会执行一个while (begin1 <= end1)temp[j++] = a[begin1++];while (begin2 <= end2)temp[j++] = a[begin2++];//归并完成,将temp的数据拷贝回去}memcpy(a, temp, sizeof(int) * n);//一起拷贝回去gap *= 2;//设置条件}
}这样对吗?测试一下
 如果我们将数加到10个呢??
如果我们将数加到10个呢??

越界了!!因为我们之前那个情况是8个元素恰好是2的次方,所以无论怎么分割再归并,都不会越界,所以这个时候我们要考虑边界情况!!

修正版本1:
void MergeSortNonR(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功int gap = 1;while (gap < n){int j = 0;//用来遍历拷贝数组for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (end1 >= n || begin2 >= n)break;if (end2 >= n)//修正end2 = n - 1;while (begin1 <= end1 && begin2 <= end2)//只要有一个先拷贝完,就跳出循环{//谁小谁尾插if (a[begin1] <= a[begin2])temp[j++] = a[begin1++];elsetemp[j++] = a[begin2++];}//这个时候其中一个区间先遍历完了,这个时候另一个没有遍历的区间插入就可以了//以下两个while只会执行一个while (begin1 <= end1)temp[j++] = a[begin1++];while (begin2 <= end2)temp[j++] = a[begin2++];//归并一次,拷贝一次memcpy(a + i, temp + i, sizeof(int) * (end2-i+1));//一起拷贝回去}gap *= 2;//设置条件}
}
修改版本2:
void MergeSortNonR2(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功int gap = 1;while (gap < n){int j = 0;//用来遍历拷贝数组for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (end1 >= n){end1 = n - 1;//修正end1//然后为了让begin2和end2不走循环,直接让他们区间不存在begin2 = n;end2 = n - 1;}else if (begin2 >= n){//不存在区间begin2 = n;end2 = n - 1;}else if (end2 >= n){ //修正end2end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2)//只要有一个先拷贝完,就跳出循环{//谁小谁尾插if (a[begin1] <= a[begin2])temp[j++] = a[begin1++];elsetemp[j++] = a[begin2++];}//这个时候其中一个区间先遍历完了,这个时候另一个没有遍历的区间插入就可以了//以下两个while只会执行一个while (begin1 <= end1)temp[j++] = a[begin1++];while (begin2 <= end2)temp[j++] = a[begin2++];}gap *= 2;//设置条件memcpy(a, temp, sizeof(int) * n);}
}1.4 归并排序的优化
假设我们的数据非常大,比如100万个数据,一开始的拆分效率是很高的,但是当数据变得很少的时候比如8个,这个时候再继续拆,效率其实很低的

我们当递归只剩大概10个元素的时候,停止递归,使用直接插入排序
void _MergeSort(int* a, int begin, int end, int* temp)
{if (begin == end)return;//设置递归返回条件if (end - begin + 1 < 10){InsertSort(a+begin, end - begin + 1);//优化return;}int mid = (begin + end) / 2;//开始分解_MergeSort(a, begin, mid, temp);//左区间归并_MergeSort(a, mid+1, end, temp);//右区间归并//开始进行总归并int begin1 = begin, end1 = mid;//设置指针指向左区间int begin2 = mid + 1, end2 = end;//设置指针指向右区间int i = begin;//用来遍历拷贝数组while (begin1 <= end1 && begin2 <= end2)//只要有一个先拷贝完,就跳出循环{//谁小谁尾插if (a[begin1] < a[begin2])temp[i++] = a[begin1++];elsetemp[i++] = a[begin2++];}//这个时候其中一个区间先遍历完了,这个时候另一个没有遍历的区间插入就可以了//以下两个while只会执行一个while (begin1 <= end1)temp[i++] = a[begin1++];while (begin2<=end2)temp[i++] = a[begin2++];//归并完成,将temp的数据拷贝回去memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));//因为递归,拷贝的不一定就是从头开始的,左闭右闭个数要+1;
}
void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功,开始进行递归_MergeSort(a, 0, n - 1, temp);
}
1.5 复杂度分析
时间复杂度:O(N*logN)
他像二叉树的后序遍历,高度是logN,每一层合计归并时O(N)遍历一遍数组
空间复杂度:O(N)
N为辅助数组的长度,和原数组的长度一样!
二、计数排序
2.1 思想
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用,是一种非比较排序!
步骤:
1、统计相同元素的出现次数
2、根据统计的结果将序列回收到原来的序列中
2.2 计数排序的实现

代码实现:
void CountSort(int* a, int n)
{int min = a[0], max = a[0];//根据最值来确定范围//遍历原数组找范围for (int i = 0; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}//确定新数组的构建范围int range = max - min + 1;int* temp = (int*)calloc(range, sizeof(int));//因为要初始化0,所以用calloc//也可以先用malloc,然后用memset(temp,0,sizeof(int)*range)if (temp == NULL){perror("calloc fail");exit(1);}//开辟成功后,开始遍历原数组计数for (int i = 0; i < n; i++)temp[a[i] - min]++;//遍历完后,计数也完成了,开始遍历计数数组,恢复原数组int k = 0;//用来恢复原数组for (int j = 0; j < range; j++)while (temp[j]--)//一直减到0,就会跳下一层循环,直到遍历完!!a[k++] = j + min;
}2.3 复杂度分析
时间复杂度:O(MAX(N,范围))
空间复杂度:O(范围)
2.4 计数排序的缺陷
1,只适合范围相对集中的数据
2、只适用与整型,因为只有整型才能和下标建立联系
三、内排序和外排序

四、稳定性

五、八大排序对比
4.1 代码实现测速度
void TestOP()//测试速度
{srand((unsigned int)time(NULL));const int N = 10000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);int* a8 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];}//clock计入程序走到当前位置的时间int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N); int end3 = clock();int begin4 = clock();BubbleSort(a4, N); int end4 = clock();int begin5 = clock();HeapSort(a5, N);int end5 = clock();int begin6 = clock();QuickSort(a6, 0, N - 1);int end6 = clock();int begin7 = clock();MergeSort(a7, N);int end7 = clock();int begin8 = clock();CountSort(a8, N);int end8 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("BubbleSort:%d\n", end4 - begin4);printf("HeapSort:%d\n", end5 - begin5);printf("QuickSort:%d\n", end6 - begin6);printf("MergeSort:%d\n", end7 - begin7);printf("CountSort:%d\n", end8 - begin8);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);free(a8);}int main()
{TestOP();
}测试一下:
N=10000

N=100000


我们发现:
希尔排序、堆排序、快排、归并排、计数牌是一个量级的
N=10000000

直接插入排、选择排序、冒泡排序是一个量级的
4.2 复杂度稳定性比较

六、八大排序全部代码
建议大家把博主的有关八大排序的代码都看一下
主要是前三个文件,后面四个文件是为了快排的栈实现和队列实现准备的!!
6.1 sort.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<time.h>
void ArrPrint(int* a, int n);//用来打印结果
void Swap(int* p1, int* p2);//进行交换void InsertSort(int* a, int n);//直接插入排序void ShellSort(int* a, int n);//希尔排序void SelectSort(int* a, int n);//选择排序void AdjustDown(int* a, int n, int parent);//向下调整算法
void HeapSort(int* a, int n);//堆排序void BubbleSort(int* a, int n);//冒泡排序int GetMidIndex(int* a, int left, int right);//快排优化——三数取中
int GetMidIndex2(int* a, int left, int right);//三数取中再优化
int PartSort1(int* a, int left, int right);//hoare基准排序
int PartSort2(int* a, int left, int right);//挖坑基准排序
int PartSort3(int* a, int left, int right);//前后指针基准排序
void QuickSort(int* a, int left, int right);//递归快排
void QuickSort2(int* a, int left, int right);//三路归并快排
void QuickSortNonR1(int* a, int left, int right);//栈实现非递归快排
void QuickSortNonR2(int* a, int left, int right);//队列实现非递归快排void HeapSort(int* a, int n);//堆排序void BubbleSort(int* a, int n);//冒泡排序void _MergeSort(int* a, int begin, int end,int *temp);//归并排序的子函数(用来递归)
void MergeSort(int* a, int n);//归并排序
void MergeSortNonR(int* a, int n);//归并排序非递归
void MergeSortNonR2(int* a, int n);//归并排序非递归版本2void CountSort(int* a, int n);//计数排序6.2 sort.c
#include"Sort.h"
#include"Stack.h"
#include"Queue.h"
void ArrPrint(int* a, int n)
{for (int i = 0; i < n; i++)printf("%d ", a[i]);
}
void Swap(int* p1, int* p2)
{int temp = *p1;*p1 = *p2;*p2 = temp;
}void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int temp = a[i+1];while (end >= 0){if (a[end] > temp)//如果前面的数比后面的数大,就前面元素插入到后面的位置a[end + 1] = a[end];elsebreak;--end;}a[end + 1] = temp;//不写在循环里面,是避免end减成-1,此时说明新加入的牌是最小的,正好放在一开始的位置}
}void ShellSort(int* a, int n)
{//gap>1 预排序//gap=1 直接插入排序int gap = n;while (gap > 1){gap = gap / 3 + 1;//这是为了保证gap最后一定为1for (int i = 0; i < n - gap; i++){int end = i;int temp = a[i + gap];while (end >= 0){if (a[end] > temp)//如果前面的数比后面的数大,就前面元素插入到后面的位置a[end + gap] = a[end];elsebreak;end -= gap;}a[end + gap] = temp;}}
}
//
void SelectSort(int* a, int n)
{int left = 0; int right = n - 1;while (left < right){int min = left;int max = left;for (int i = left+1; i <= right; i++){if (a[min] > a[i])min = i;if (a[max] < a[i])max = i;}//这里要考虑一种情况,就是如果最大的数恰好就在最左端,那么就会导致第二次swap换到后面的就不是最大的数而是最小的数了Swap(&a[min], &a[left]);//如果max和begin重叠,修正一下if (max == left)max = min;Swap(&a[max], &a[right]);left++;right--;}
}int GetMidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right])return mid;else if (a[right] < a[left])return left;elsereturn right;}else//a[left] >a[mid]{if (a[mid] > a[right])return mid;else if (a[right] > a[left])return left;elsereturn right;}
}int GetMidIndex2(int* a, int left, int right)
{int mid = left + (rand() % (right - left));if (a[left] < a[mid]){if (a[mid] < a[right])return mid;else if (a[right] < a[left])return left;elsereturn right;}else//a[left] >a[mid]{if (a[mid] > a[right])return mid;else if (a[right] > a[left])return left;elsereturn right;}
}int PartSort1(int* a, int left, int right)//hoare基准排序
{int mid=GetMidIndex(a, left, right);Swap(&a[mid], &a[left]);int keyi = left;while (left < right){//右先找比key大的while (left < right&&a[right] >= a[keyi])right--;//左找比key小的while (left < right && a[left] <= a[keyi])left++;//找到后,就交换Swap(&a[left], &a[right]);}//此时相遇了,把相遇的位置和keyi的位置交换Swap(&a[left], &a[keyi]);return left;
}int PartSort2(int* a, int left, int right)//挖坑基准排序
{int mid = GetMidIndex(a, left, right);Swap(&a[mid], &a[left]);int key = a[left];//记住key的值int hole = left;//开始挖坑while (left < right){//右先找比key大的while (left < right && a[right] >= key)right--;//找到后,填坑,然后挖新坑a[hole] = a[right];hole = right;//左找比key小的while (left < right && a[left] <= key)left++;//找到后,填坑,然后挖新坑a[hole] = a[left];hole = left;}//此时相遇了,把key值放在坑里a[hole] = key;return hole;
}int PartSort3(int* a, int left, int right) //前后指针基准排序
{int mid = GetMidIndex(a, left, right);Swap(&a[mid], &a[left]);int prev = left;int cur = left + 1;int keyi = left;while (cur <= right)//cur走出数组循环停止{//cur一直在走,如果遇到比keyi小的,就停下来等perv走一步后交换,再接着走if (a[cur] < a[keyi]&&++prev!=cur)Swap(&a[prev], &a[cur]);cur++;}//cur出去后,prev的值和keyi交换Swap(&a[keyi], &a[prev]);return prev;
}void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyi = PartSort1(a, left, right);//根据基准值去分割区间,继续进行基准排序QuickSort(a, left, keyi - 1);QuickSort(a, keyi+1,right);
}void QuickSort2(int* a, int left, int right)
{if (left >= right)return;int mid = GetMidIndex2(a, left, right);Swap(&a[mid], &a[left]);int phead = left;int pcur = left + 1;int ptail = right;int key = a[left];while (pcur <= ptail){if (a[pcur] < key){Swap(&a[pcur], &a[phead]);pcur++;phead++;}else if (a[pcur] > key){Swap(&a[pcur], &a[ptail]);ptail--;}else//a[pcur] = keypcur++;}QuickSort2(a, left, phead - 1);QuickSort2(a, ptail+1,right);
}void QuickSortNonR1(int* a, int left, int right)
{Stack st;StackInit(&st);//把区间压进去,一定要先压右区间!!StackPush(&st, right);StackPush(&st, left);while (!StackEmpty(&st)){//将数据弹出来进行进准计算int left = StackTop(&st);StackPop(&st);int right= StackTop(&st);StackPop(&st);//进行基准计算int keyi = PartSort3(a, left, right);//分割区间(left keyi-1)keyi(keyi+1,right)//如果对应的区间还能分割,就继续压,要注意要先压后面在压前面if (keyi + 1 < right){StackPush(&st, right);StackPush(&st, keyi+1);}if (keyi - 1 > left){StackPush(&st, keyi-1);StackPush(&st,left);}}//会一直到栈为空,此时就拍好序了!!StackDestory(&st);
}void QuickSortNonR2(int* a, int left, int right)
{Queue q;QueueInit(&q);QueuePush(&q, left);QueuePush(&q, right);while (!QueueEmpty(&q)){int left = QueueFront(&q);QueuePop(&q);int right = QueueFront(&q);QueuePop(&q);int keyi = PartSort3(a, left, right);if (keyi - 1 > left){QueuePush(&q, left);QueuePush(&q, keyi-1);}if (keyi + 1 <right){QueuePush(&q, keyi +1);QueuePush(&q, right);}}QueueDestory(&q);
}//向下调整算法
void AdjustDown(int* a, int n, int parent)//升序要建大堆
{int child = parent * 2 + 1;//假设左孩子比右孩子大while (child < n){//如果假设错误,就认错if (child + 1 < n && a[child] < a[child + 1])child++;//如果孩子大于父亲,交换if (a[child] > a[parent]){Swap(&a[child], &a[parent]);//交换完后,让原来的孩子变成父亲,然后再去找新的孩子parent = child;child = parent * 2 + 1;}elsebreak;}
}void HeapSort(int* a, int n)
{//向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--)AdjustDown(a, n, i);//大堆,向下调整int end = n - 1;while (end >= 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; i++)//每一趟拍好一个,最后排完n-1个,最后一个数就没必要比了{int flag = 1;//假设有序for (int j = 0; j < n - i - 1; j++)//第一趟需要比较的n-1次,第二次需要比较n-2次……//所以结束条件跟着i变化{if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);flag = 0;//如果没有发生交换,说明不符合有序}}if (flag == 1)break;}
}void _MergeSort(int* a, int begin, int end, int* temp)
{if (begin == end)return;//设置递归返回条件if (end - begin + 1 < 10){InsertSort(a+begin, end - begin + 1);//优化return;}int mid = (begin + end) / 2;//开始分解_MergeSort(a, begin, mid, temp);//左区间归并_MergeSort(a, mid+1, end, temp);//右区间归并//开始进行总归并int begin1 = begin, end1 = mid;//设置指针指向左区间int begin2 = mid + 1, end2 = end;//设置指针指向右区间int i = begin;//用来遍历拷贝数组while (begin1 <= end1 && begin2 <= end2)//只要有一个先拷贝完,就跳出循环{//谁小谁尾插if (a[begin1] < a[begin2])temp[i++] = a[begin1++];elsetemp[i++] = a[begin2++];}//这个时候其中一个区间先遍历完了,这个时候另一个没有遍历的区间插入就可以了//以下两个while只会执行一个while (begin1 <= end1)//等于才能保证稳定性!!temp[i++] = a[begin1++];while (begin2<=end2)temp[i++] = a[begin2++];//归并完成,将temp的数据拷贝回去memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));//因为递归,拷贝的不一定就是从头开始的,左闭右闭个数要+1;
}
void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功,开始进行递归_MergeSort(a, 0, n - 1, temp);
}void MergeSortNonR(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功int gap = 1;while (gap < n){int j = 0;//用来遍历拷贝数组for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (end1 >= n || begin2 >= n)break;if (end2 >= n)//修正end2 = n - 1;while (begin1 <= end1 && begin2 <= end2)//只要有一个先拷贝完,就跳出循环{//谁小谁尾插if (a[begin1] <= a[begin2])temp[j++] = a[begin1++];elsetemp[j++] = a[begin2++];}//这个时候其中一个区间先遍历完了,这个时候另一个没有遍历的区间插入就可以了//以下两个while只会执行一个while (begin1 <= end1)temp[j++] = a[begin1++];while (begin2 <= end2)temp[j++] = a[begin2++];//归并一次,拷贝一次memcpy(a + i, temp + i, sizeof(int) * (end2-i+1));//一起拷贝回去}gap *= 2;//设置条件}
}void MergeSortNonR2(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(1);}//开辟成功int gap = 1;while (gap < n){int j = 0;//用来遍历拷贝数组for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (end1 >= n){end1 = n - 1;//修正end1//然后为了让begin2和end2不走循环,直接让他们区间不存在begin2 = n;end2 = n - 1;}else if (begin2 >= n){//不存在区间begin2 = n;end2 = n - 1;}else if (end2 >= n){ //修正end2end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2)//只要有一个先拷贝完,就跳出循环{//谁小谁尾插if (a[begin1] <= a[begin2])temp[j++] = a[begin1++];elsetemp[j++] = a[begin2++];}//这个时候其中一个区间先遍历完了,这个时候另一个没有遍历的区间插入就可以了//以下两个while只会执行一个while (begin1 <= end1)temp[j++] = a[begin1++];while (begin2 <= end2)temp[j++] = a[begin2++];}gap *= 2;//设置条件memcpy(a, temp, sizeof(int) * n);}
}void CountSort(int* a, int n)
{int min = a[0], max = a[0];//根据最值来确定范围//遍历原数组找范围for (int i = 0; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}//确定新数组的构建范围int range = max - min + 1;int* temp = (int*)calloc(range, sizeof(int));//因为要初始化0,所以用calloc//也可以先用malloc,然后用memset(temp,0,sizeof(int)*range)if (temp == NULL){perror("calloc fail");exit(1);}//开辟成功后,开始遍历原数组计数for (int i = 0; i < n; i++)temp[a[i] - min]++;//遍历完后,计数也完成了,开始遍历计数数组,恢复原数组int k = 0;//用来恢复原数组for (int j = 0; j < range; j++)while (temp[j]--)//一直减到0,就会跳下一层循环,直到遍历完!!a[k++] = j + min;
}6.3 test.c
#include"Sort.h"void TestOP()//测试速度
{srand((unsigned int)time(NULL));const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);int* a8 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];}//clock计入程序走到当前位置的时间int begin1 = clock();//InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();//SelectSort(a3, N); int end3 = clock();int begin4 = clock();//BubbleSort(a4, N); int end4 = clock();int begin5 = clock();HeapSort(a5, N);int end5 = clock();int begin6 = clock();QuickSort(a6, 0, N - 1);int end6 = clock();int begin7 = clock();MergeSort(a7, N);int end7 = clock();int begin8 = clock();CountSort(a8, N);int end8 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("BubbleSort:%d\n", end4 - begin4);printf("HeapSort:%d\n", end5 - begin5);printf("QuickSort:%d\n", end6 - begin6);printf("MergeSort:%d\n", end7 - begin7);printf("CountSort:%d\n", end8 - begin8);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);free(a8);}int main()
{TestOP();
}6.4 stack.h
#pragma once
#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<assert.h>typedef int STDataType;
//支持动态增长的栈
typedef struct Stack
{STDataType* a;int top;//栈顶int capacity;//栈容量
}Stack;void StackInit(Stack* ps);//初始化栈
void StackPush(Stack* ps, STDataType x);//入栈
void StackPop(Stack* ps);//出栈
STDataType StackTop(Stack* ps);//获取栈顶元素
int StackSize(Stack* ps);//获取栈中有效元素个数
bool StackEmpty(Stack* ps);//检测栈是否为空,为空返回true
void StackDestory(Stack* ps);//销毁栈6.5 stack.c
#include"Stack.h"void StackInit(Stack* ps)
{ps->a = NULL;ps->top = ps->capacity = 0;
}void StackPush(Stack* ps, STDataType x)
{assert(ps);//判断是否需要扩容if (ps->top == ps->capacity){int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* temp = (STDataType*)realloc(ps->a,sizeof(STDataType) * newcapacity);if (temp == NULL){perror("realloc fail");exit(1);}ps->a = temp;ps->capacity = newcapacity;}//压栈ps->a[ps->top++] = x;
}void StackPop(Stack* ps)
{assert(ps);//如果栈为空,则没有删除的必要assert(!StackEmpty(ps));ps->top--;
}STDataType StackTop(Stack* ps)
{assert(ps);//如果栈为空,不可能有栈顶元素assert(!StackEmpty(ps));return ps->a[ps->top - 1];
}int StackSize(Stack* ps)
{assert(ps);return ps->top;
}bool StackEmpty(Stack* ps)
{assert(ps);return ps->top == 0;
}void StackDestory(Stack* ps)
{free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}6.6 queue.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int QDatatype;//方便后面修改存储数据的数据类型
typedef struct QueueNode//队列结点的数据结构
{QDatatype data;//存储数据struct QueueNode* next;
}QNode;typedef struct Queue
{QNode* phead;//指向队头,用于出队(头删)QNode* ptail;//指向队尾,用于入队(尾插)int size;//记录有效元素个数
}Queue;//创建一个队列相关结构体
void QueueInit(Queue* pq);//队列的初始化
void QueuePush(Queue* pq, QDatatype x);//队列的入队(尾插)
void QueuePop(Queue* pq);//队列的出队(头删)
QDatatype QueueFront(Queue* pq);//获取队列头部元素
QDatatype QueueBack(Queue* pq);//获取队列尾部元素
int QueueSize(Queue* pq);//获取队列中有效元素个数
bool QueueEmpty(Queue* pq);//判断队列是否为空
void QueueDestory(Queue* pq);//队列的销毁6.7 queue.c
#include"Queue.h"void QueueInit(Queue* pq)
{assert(pq);//判断传的是不是空指针pq->phead = pq->ptail = NULL;pq->size = 0;//因为队列不像栈一样,有一个top表示栈顶元素的下标//所以如果我们想知道这个队列的有效数据个数,就必须遍历队列//由于其先进先出的特性,我们默认只能访问到头元素和尾元素//所以必须访问一个头元素,就出队列一次,这样才能实现遍历//但是这样的代价太大了,为了方便,我们直接用size
}void QueuePush(Queue* pq, QDatatype x)
{assert(pq);//入队必须从队尾入!QNode* newnode = (QNode*)malloc(sizeof(QNode));//创建一个新节点if (newnode==NULL)//如果新节点申请失败,退出程序{perror("malloc fail");}//新节点创建成功,给新节点初始化一下newnode->data = x;newnode->next = NULL;//开始入队//如果直接尾插的话,由于会用到ptail->next,所以得考虑队列为空的情况if (pq->ptail== NULL)//如果为空,直接把让新节点成为phead和ptail{//按道理来说,如果ptail为空,phead也应该为空// 但是有可能会因为我们的误操作使得phead不为空,这个时候一般是我们写错的问题//所以使用assert来判断一下,有问题的话会及时返回错误信息assert(pq->phead == NULL);pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}void QueuePop(Queue* pq)
{assert(pq);//如果队列为空,没有删除的必要assert(!QueueEmpty(pq));//队列中的出队列相当于链表的头删//如果直接头删,那么如果队列只有一个有效数据的话,那么我们将phead的空间释放掉,但是没有将ptail给置空//这样会导致ptail成为一个野指针,所以我们需要考虑只有一个节点多个节点的情况if (pq->phead->next == NULL)//一个节点的情况,直接将这个节点释放并置空即可{free(pq->phead);pq->phead = pq->ptail = NULL;//置空,防止野指针}else//多个节点的情况,直接头删{QNode* next = pq->phead->next;//临时指针记住下一个节点free(pq->phead);pq->phead = next;//让下一个节点成为新的头}pq->size--;
}QDatatype QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));//队列如果为空,则不可能找得到队列头元素//队列不为空的时候,直接返回phead指向的数据return pq->phead->data;
}QDatatype QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));//队列如果为空,则不可能找得到队尾元素//队列不为空的时候,直接返回ptail指向的数据return pq->ptail->data;
}int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}bool QueueEmpty(Queue* pq)//链表为空的情况,可以根据容量,也可以根据ptail==NULL&&phead==NULL
{assert(pq);return pq->ptail == NULL && pq->phead == NULL;
}void QueueDestory(Queue* pq)
{assert(pq);//判断传的是不是空指针//要逐个节点释放QNode* pcur = pq->phead;while (pcur){QNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
相关文章:

DS:八大排序之归并排序、计数排序
创作不易,感谢三连支持!! 一、归并排序 1.1 思想 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子…...
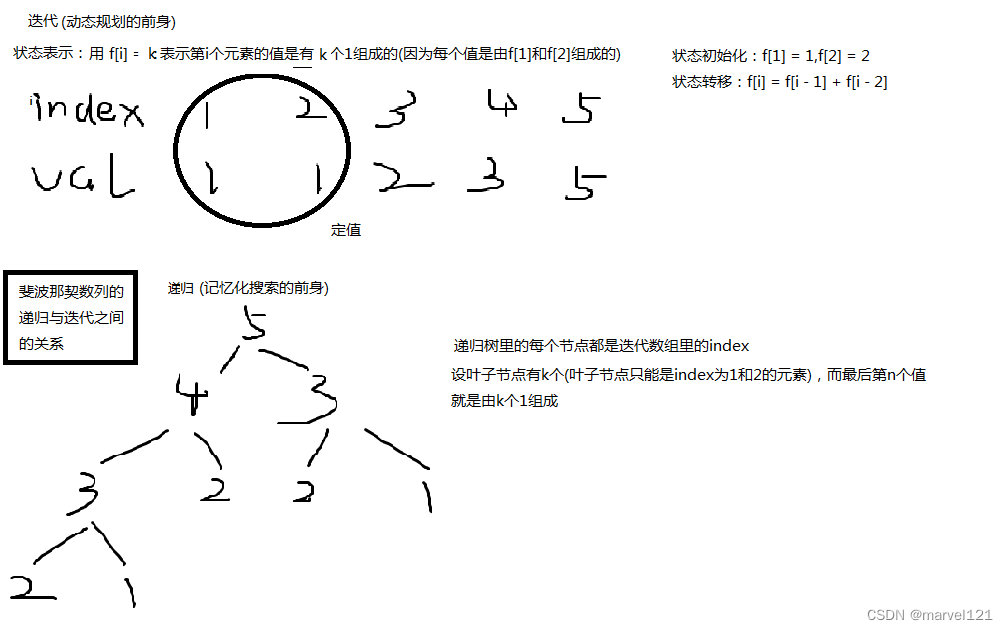
由斐波那契数列探究递推与递归
斐波那契数列定义: 斐波那契数列大家都非常熟悉。它的定义是: 对于给定的整数 x ,我们希望求出: f ( 1 ) f ( 2 ) … f ( x ) f(1)f(2)…f(x) f(1)f(2)…f(x) 的值。 有两种方法,分别是递推(迭代)与递归 具体解释如下图 备注…...

红队打靶练习:IMF: 1
目录 信息收集 1、arp 2、nmap 3、nikto 目录探测 gobuster dirsearch WEB 信息收集 get flag1 get flag2 get flag3 SQL注入 漏洞探测 脱库 get flag4 文件上传 反弹shell 提权 get flag5 get flag6 信息收集 1、arp ┌──(root㉿ru)-[~/kali] └─# a…...
?)
密码管理局以及什么是密评?为什么要做密评(商用密码应用安全性评估)?
文章目录 密码管理局以及什么是密评?为什么要做密评?关于密码管理局国家密码管理局属于什么级别?什么是密评?密评发展史为什么要做密评?目前密码应用的几个问题密评对象不做“密评”或密评不合格有什么影响?如何才能顺利通过密评?密评的相关标准参考密码管理局以及什么是…...
六、Datax通过json字符串运行
Datax通过json字符串运行 一、场景二、代码实现 一、场景 制作一个web应用,在页面上配置一个json字符串,保存在数据库里面。在执行json的时候,动态在本地创建一个json文件后执行,并识别是否成功,将执行过程保存在数据…...

关于数据库
目录 一 什么是数据库(DB) 二 什么是数据库管理系统(DBMS) 三 数据库的作用/好处 一 什么是数据库(DB) 简单理解,数据库是存放数据的地方,就像冰箱是存放冷鲜食品的地方。 数据是数据存储的基本对象,而数据分为多…...
洛谷C++简单题小练习day14—闰年推算小程序
day14--闰年推算小程序--2.18 习题概述 题目描述 输入 x,y,输出 [x,y] 区间中闰年个数,并在下一行输出所有闰年年份数字,使用空格隔开。 输入格式 输入两个正整数 x,y,以空格隔开。 输出格式 第一行输出一个正整数…...
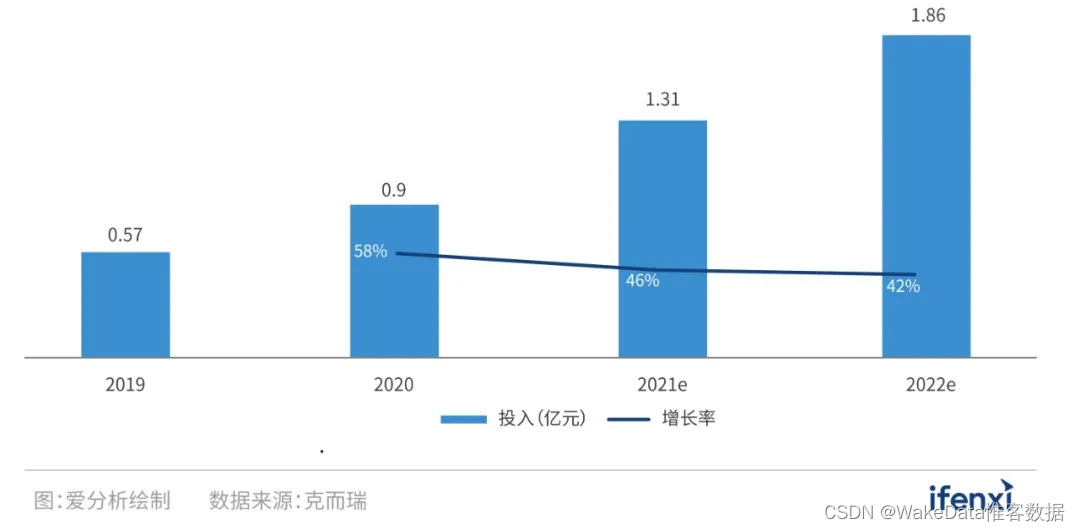
房企关注的典型数字化场景之一:数字营销
过去在增量时代下,房企的模式是“拿地-开发-卖房-拿地”,谁拿的地多、卖得快、利润高,谁“活得好”。而进入存量时代,加上政策调控影响,房企需要将核心竞争力转向精细化、多元化运营。 根据克而瑞数据统计,…...
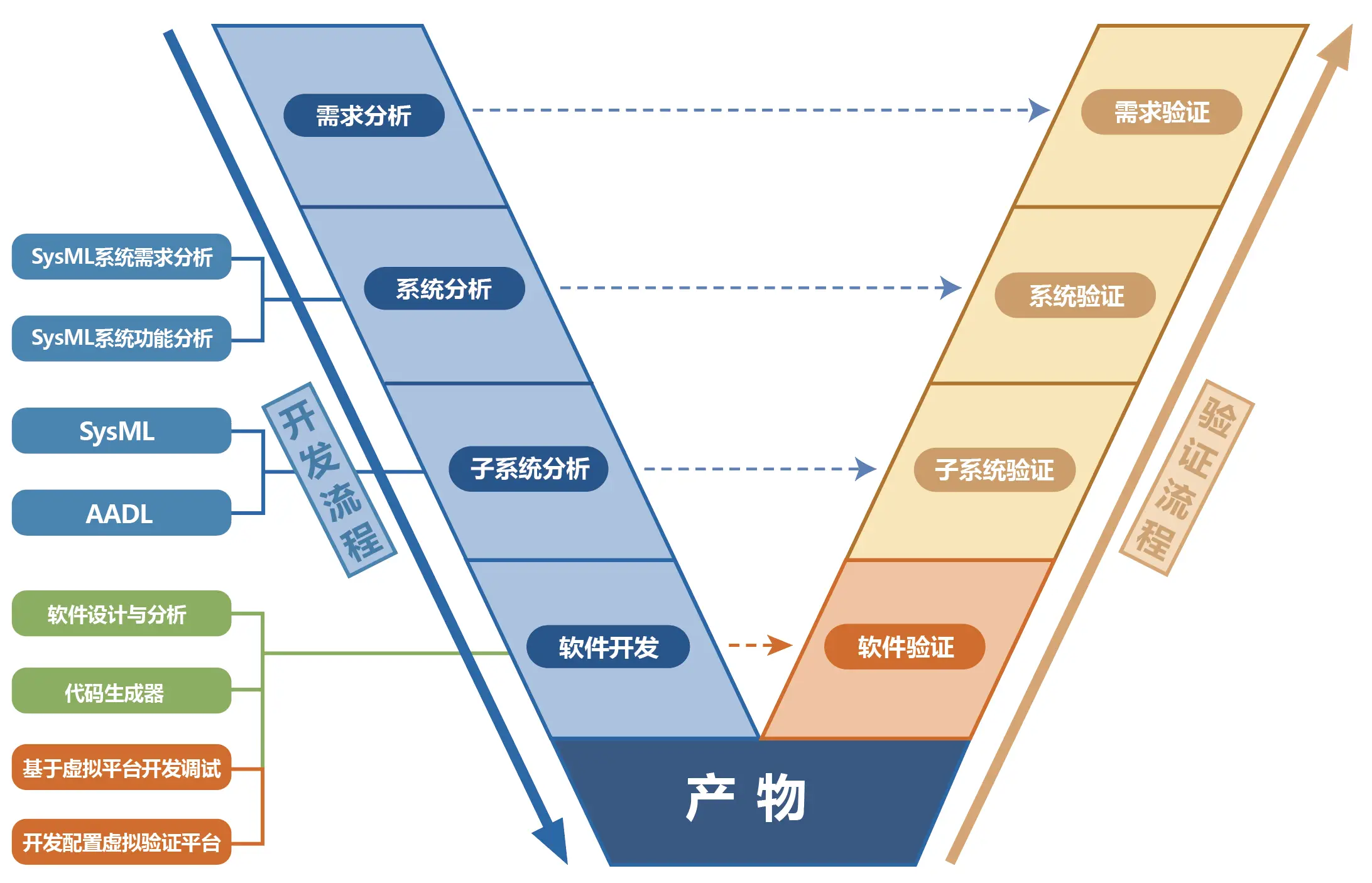
BMS再进阶(新能源汽车电池管理系统)
引言 一文入门BMS(电池管理系统)_bms电池管理-CSDN博客 BMS进阶(Type-C、PD快充、充电IC、SOC算法、电池管理IC)_充电ic asi aso功能-CSDN博客 本文是上面两篇博客的续篇,之前都是讲解一些BMS基本原理,…...

K8s Deployment挂载ConfigMap权限设置
目录 样例 1. 样例 …… volumes: - configMap:defaultMode: 420name: ${Existed_configmap_name} …… 其中“defaultMode: 420”是设置权限的 2. 解析 在K8s(Kubernetes)中,defaultMode是用来设置Configmap挂载后的文件权限࿰…...

百度智能云分布式数据库 GaiaDB-X 与龙芯平台完成兼容认证
近日,百度智能云的分布式关系型数据库软件 V3.0 与龙芯中科技术股份有限公司的龙芯 3C5000L/3C5000 处理器平台完成兼容性测试,功能与稳定性良好,获得了龙架构兼容互认证证书。 龙芯系列处理器 通用 CPU 处理器是信息产业的基础部件…...
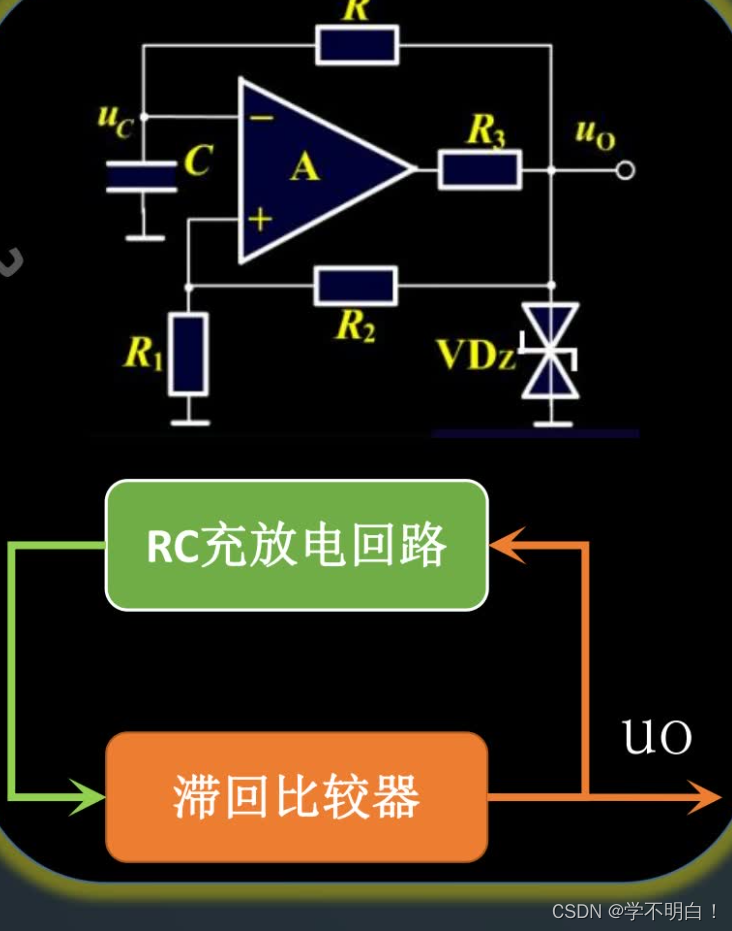
模拟电子技术——振荡器基本原理、RC桥式振荡器、矩形波发生电器
文章目录 前言一、振荡器什么是振荡器振荡器的基本电路结构振荡条件起振条件和稳幅原理 二、RC桥式振荡器什么是RC桥式振荡器RC串并联网络的选频特性振荡条件完整频率特性曲线举例 三、矩形波发生电器什么是矩形波发生电路稳态与暂态PWM脉宽调制矩形波发生电路基本组成 总结 前…...
Vue3+Vite+TS+Pinia+ElementPlus+Router+Axios创建项目
目录 初始项目组成1. 创建项目1.1 下载项目依赖1.2 项目自动启动1.3 src 别名设置vite.config.ts配置文件tsconfig.json配置若新创项目ts提示 1.4 运行测试 2. 清除默认样式2.1 样式清除代码下载2.2 src下创建公共样式文件夹style2.3 main.js中引入样式2.4 安装sass解析插件 2.…...

VMware虚拟机安装CentOS7
对于系统开发来说,开发者时常会需要涉及到不同的操作系统,比如Windows系统、Mac系统、Linux系统、Chrome OS系统、UNIX操作系统等。由于在同一台计算机上安装多个系统会占据我们大量的存储空间,所以虚拟机概念应运而生。本篇将介绍如何下载安…...
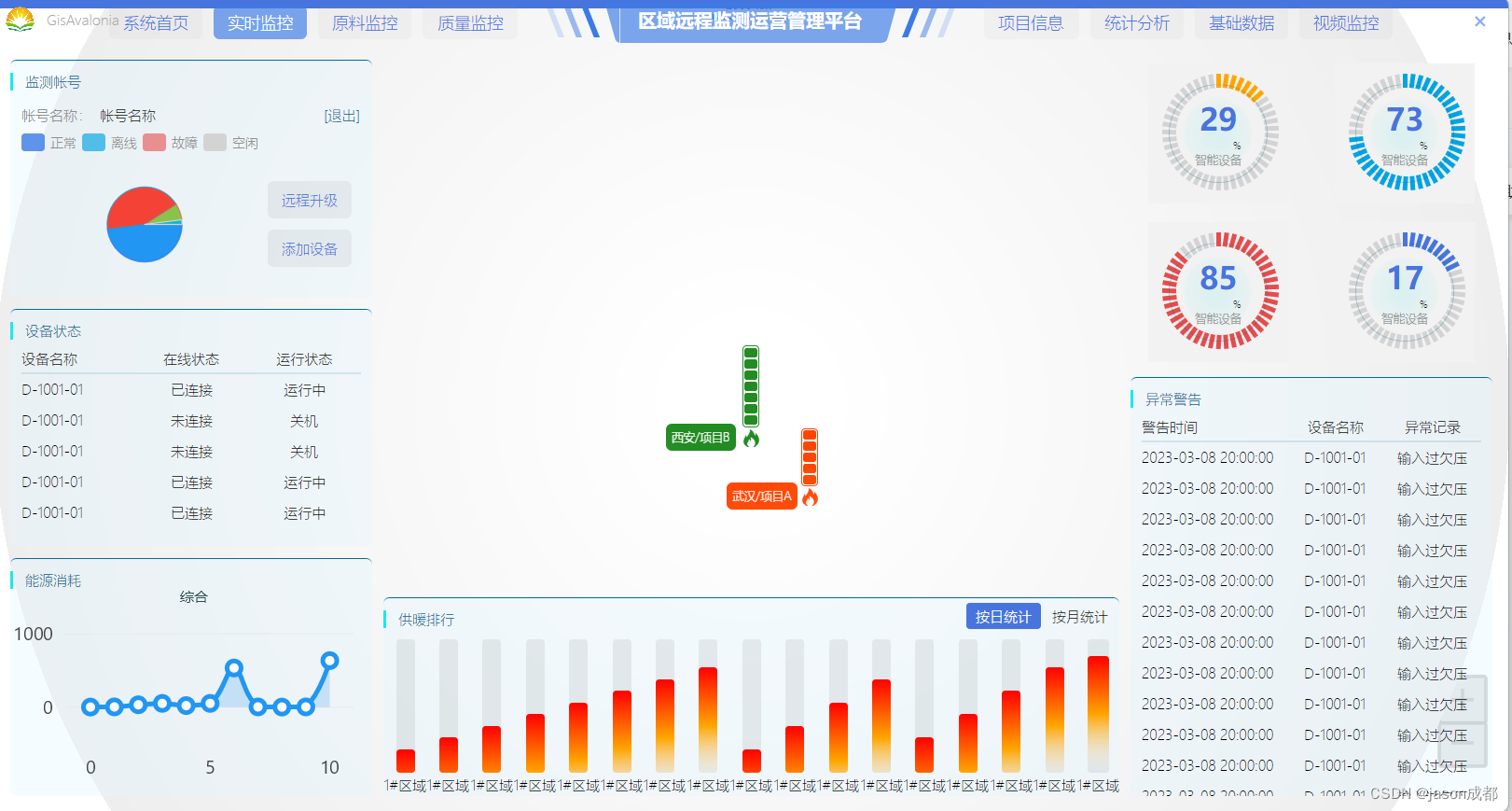
Avalonia学习(二十四)-系统界面
目前项目式练习,界面内容偏多,所以不给大家贴代码了,可以留言交流。此次为大家展示的是物联项目的例子,仅仅是学习,我把一些重点列举一下。 界面无边框 以前的样例主要是通过实现控件来完成的,前面已经有窗…...

深入解析鸿蒙系统的页面路由(Router)机制
鸿蒙系统以其独特的分布式架构和跨设备的统一体验而备受瞩目。在这个系统中,页面路由(Router)机制是连接应用各页面的关键组成部分。本文将深入探讨鸿蒙系统的页面路由,揭示其工作原理、特点以及在应用开发中的实际应用。 1. 实现…...

MCU中断响应流程及注意事项
本文介绍MCU中断响应流程及注意事项。 1.中断响应流程 中断响应的一般流程为: 1)断点保护 硬件操作,将PC,PSR等相关寄存器入栈保护 2)识别中断源 硬件操作,识别中断的来源,如果多个中断同时发生,高优…...
基于Java SSM框架实现网上报名系统项目【项目源码+论文说明】计算机毕业设计
基于java的SSM框架实现网上报名系统演示 摘要 随着互联网时代的到来,同时计算机网络技术高速发展,网络管理运用也变得越来越广泛。因此,建立一个B/S结构的网上报名系统,会使网上报名系统工作系统化、规范化,也会提高网…...

Eclipse - Formatter
Eclipse - Formatter References Window -> Preferences -> C/C -> Code Style -> Formatter BSD/Allman [built-in] or K& R [built-in] References [1] Yongqiang Cheng, https://yongqiang.blog.csdn.net/...

算法练习-01背包问题【含递推公式推导】(思路+流程图+代码)
难度参考 难度:困难 分类:动态规划 难度与分类由我所参与的培训课程提供,但需 要注意的是,难度与分类仅供参考。且所在课程未提供测试平台,故实现代码主要为自行测试的那种,以下内容均为个人笔记࿰…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

