linux基础学习(10):基本权限与相关命令
1.基本权限
用ls -l查看当前目录文件时,可以看到文件的基本权限

其由10位组成,其中:
第1位:代表文件类型。
| - | d | l | b | c |
| 普通文件 | 目录文件 | 软链接文件 | 块设备文件,也就是硬盘等存储设备的文件 | 字符设备文件,是鼠标键盘等输入设备的文件 |
第2到4位(u):代表文件所属者的权限
第5到7位(g):代表文件所属者的用户组的权限
第8到10位(o):代表其他用户的权限
rwx分别代表可读可写可执行
| 文件 | 文件夹 | |
| 可读r | 文件可以打开查看 可以对文件执行cat、more、less等命令 | 可以查看目录下内容(ls) |
| 可写w | 可以对文件内容进行增删 可以用vim命令编辑文件 w权限并不能删除文件 | 可以对目录下的文件进行创建(touch)、删除(rm)、复制(cp)、剪切(mv)等操作 |
| 可执行x | 运行文件 一个文件是否能够运行取决于很多因素,x权限只是其中之一 | 可以进入文件夹(cd) |
对目录而言,只有0、5、7三种权限。对w来说,r、x是必备的,对r来说,x是必备的
2.相关命令
2.1更改文件权限命令:chmod
格式:chmod -R 权限选项 文件名/文件夹名
-R:递归更改文件夹及其所有的文件权限
权限选项:rwx可以视为3位二进制数,r=4,w=2,x=1。基本权限中的u、g、o可以写成三组rwx相加的和,比如644、755、777
赋予文件满权限777会很危险,除了系统中极少的一部分文件外,不要把文件设为777
2.2更改文件所属者命令:chown
格式:chown -R 所有者:所属组 文件/文件夹
-R:递归更改文件夹及其所有的文件所属者
在使用时可以只更改所有者或只更改所属组
只有root可以更改文件所属者,否则哪怕是文件的所有者也不可以更改文件所属。但普通用户可以用chmod更改自己文件的权限
相关文章:

linux基础学习(10):基本权限与相关命令
1.基本权限 用ls -l查看当前目录文件时,可以看到文件的基本权限 其由10位组成,其中: 第1位:代表文件类型。 - d lbc普通文件目录文件软链接文件块设备文件,也就是硬盘等存储设备的文件字符设备文件,是鼠…...

木马植入方式及防范手段
木马植入方式: 1. 诱骗下载和安装:通过欺骗、社交工程等手段,诱使用户下载和安装包含木马的软件或文件。 2. 隐秘附加:将木马隐藏在合法软件的背后,并伴随软件一起安装,用户在不知情的情况下也会安装木马。…...

Unity3D中刚体、碰撞组件、物理组件的区别详解
前言 Unity3D提供了丰富的功能和组件,其中包括刚体、碰撞组件和物理组件。这些组件在游戏开发中起着非常重要的作用,能够让游戏世界更加真实和有趣。本文将详细介绍这三种组件的区别以及如何在Unity3D中实现它们。 对惹,这里有一个游戏开发…...
Java实现Redis延时队列
“如何实现Redis延时队列”这个面试题应该也是比较常见的,解答如下: 使用sortedset(有序集合) ,拿时间戳作为 score ,消息内容作为key 调用 zadd 来生产消息,消费者用zrangebyscore 指令获取 N …...

Selenium折线图自动化测试
目录 获取折线图echarts实例 获取折线图实例锚点的坐标 通过echarts实例的getOption()方法获取坐标数据 将折线图坐标点转换为像素坐标值 整合折线图坐标数据 根据折线图坐标计算出锚点相对于浏览器中的坐标 计算canvas画布原点的坐标 计算折线图相对于浏览器的坐标 使用…...
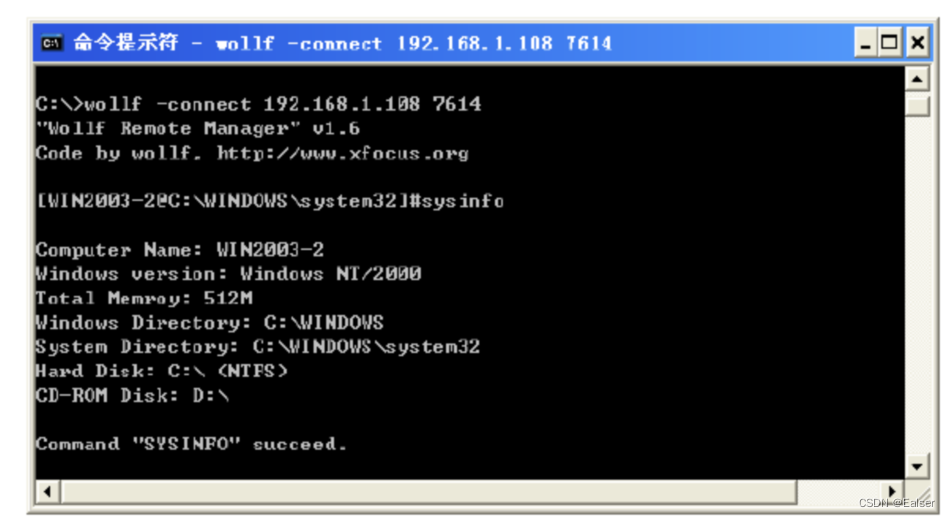
<网络安全>《41 网络攻防专业课<第七课 - IIS上传和Tomcat弱口令漏洞攻击与防范>》
1 中间件PUT漏洞介绍 中间件包括apache、tomcat、IIS、weblogic等,这些中间件可以设置支持的HTTP方法。(HTTP方法包括GET、POST、HEAD、DELETE、PUT、OPTIONS等) 每一个HTTP方法都有其对应的功能,在这些方法中,PUT可…...

云计算基础-虚拟化概述
虚拟化概述 虚拟化是一种资源管理技术,能够将计算机的各种实体资源(如CPU、内存、磁盘空间、网络适配器等)予以抽象、转换后呈现出来并可供分割、组合为一个或多个逻辑上的资源。这种技术通过在计算机硬件上创建一个抽象层,将单台…...

ElementUI +++ Echarts面试题答案汇总
官网地址:http://element-cn.eleme.io/#/zh-CN ElementUI是一套基于VUE2.0的桌面端组件库,ElementUI提供了丰富的组件帮助开发人员快速构建功能强大、风格统一的页面。 ElementUi是怎么做表单验证的?在循环里对每个input验证怎么做呢&#x…...
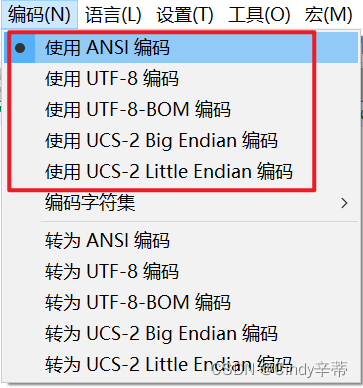
notepad++打开文本文件乱码的解决办法
目录 第一步 在编码菜单栏下选择GB2312中文。如果已经选了忽略这一步 第二步 点击编码,红框圈出来的一个个试。我切换到UTF-8编码就正常了。 乱码如图。下面分享我的解决办法 第一步 在编码菜单栏下选择GB2312中文。如果已经选了忽略这一步 第二步 点击编码&#…...

道可云元宇宙每日资讯|上海开放大学发布“智慧学习中心元宇宙”
道可云元宇宙每日简报(2024年2月19日)讯,今日元宇宙新鲜事有: 上海开放大学发布“智慧学习中心元宇宙” 上海开放大学首次发布了“智慧学习中心元宇宙”,初步构筑了上海开放大学5g元宇宙孪生学习环境,13所…...

压缩感知(Compressed Sensing,CS)的基础知识
压缩感知(Compressed Sensing,CS)是一种用于信号处理的技术,旨在以少于奈奎斯特采样定理所要求的样本频率来重构信号。该技术利用信号的稀疏性,即信号可以用较少的非零系数表示。压缩感知在图像获取中的应用使得在采集…...

如何系统地学习Python
建议系统学习Python的途径遵循理论与实践相结合的教学方法。以下是一个分阶段的学习计划: 阶段一:基础知识 理解Python的特点: 认识Python的历史与设计哲学。学习Python的基本语法和运行环境。 安装Python: 学习如何在不同操作系…...

SMT2020:半导体制造流程标准仿真测试数据介绍
文章目录 问题背景SMT2020 涉及的主要功能1. 包含多种仿真模型类型2. 包含非计划性动作3. 区分不同类型设备的加工速率4. 特殊的复杂操作SMT2020 数据概览1. AutoSched 仿真模型数据2. General Data 输入数据问题背景 在半导体的生产制造当中,由于晶元片及设备等的高价值性,…...
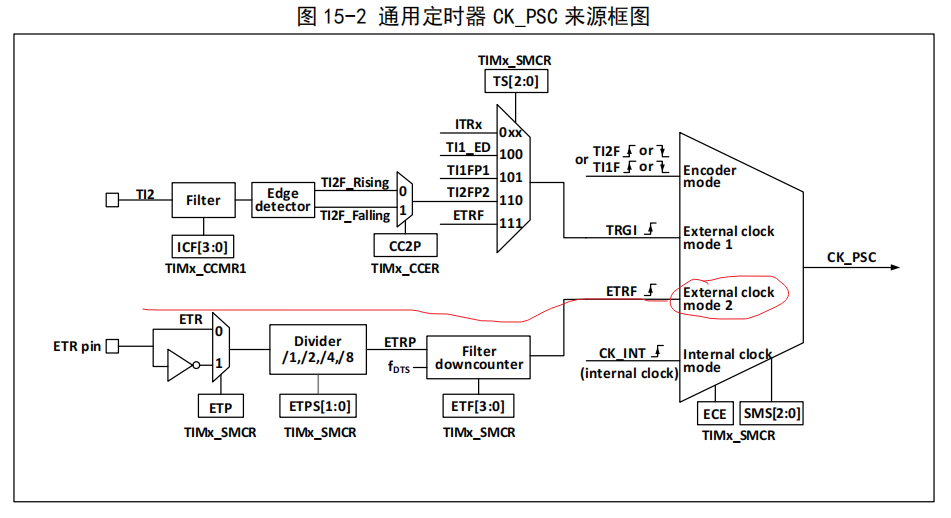
沁恒CH32V30X学习笔记11---使用外部时钟模式2采集脉冲计数
使用外部时钟模式2采集脉冲计数 使用外部触发模式 2 能在外部时钟引脚输入的每一个上升沿或下降沿计数。将 ECE 位置位时,将使用外部时钟源模式 2。使用外部时钟源模式 2 时,ETRF 被选定为 CK_PSC。ETR 引脚经过可选的反相器(ETP),分频器(ETPS)后成为 ETRP,再经过滤波…...
ffmpeg for android编译全过程与遇到的问题
编译前准备 编译环境:Ubuntu16,可自行下载VMWare最新版并百度永久许可证或在服务器上安装Ubuntu ffmpeg源码:ffmpeg4.2.2 NDK下载:Android NDK r21e 有条件的最好还是在Liunx平台下编译吧,Windows平台下编译坑更多…...
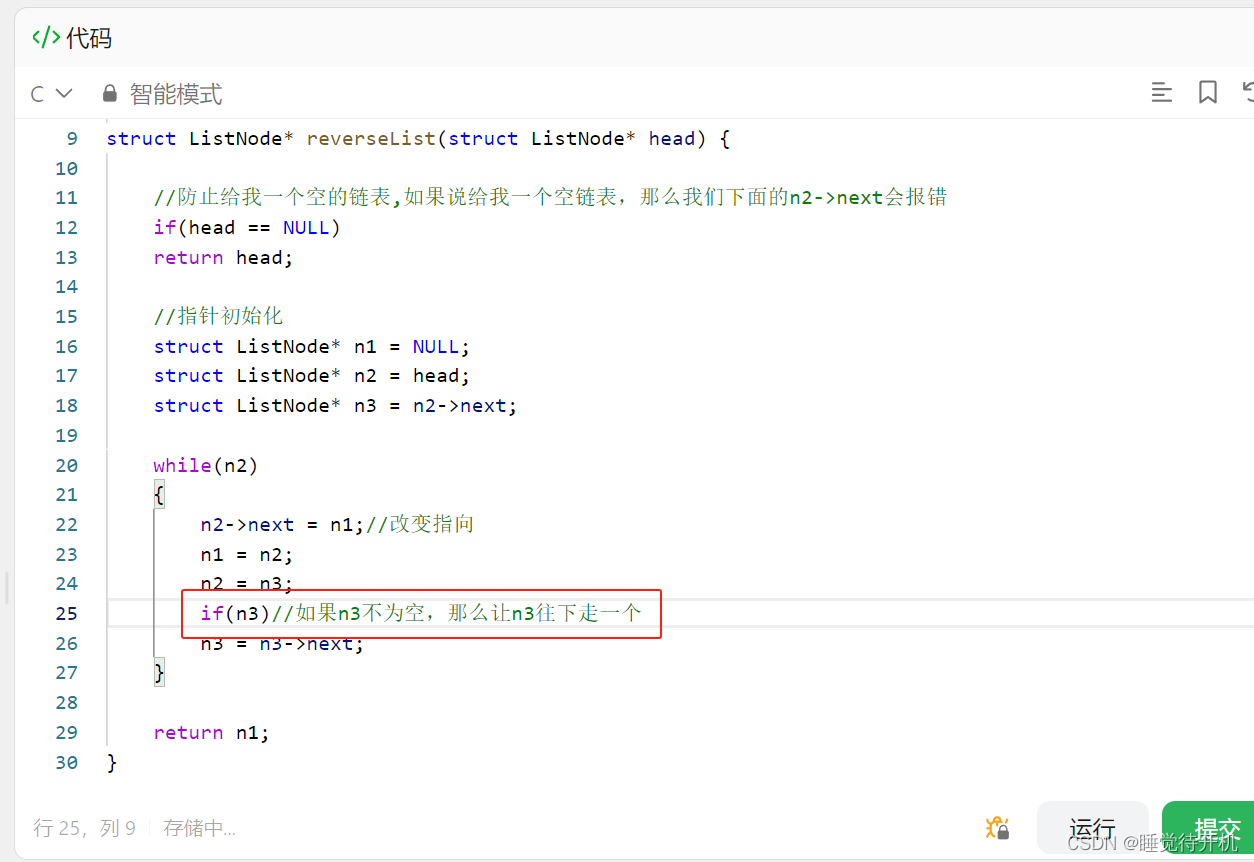
【无标题】力扣报错:member access within null pointer of type ‘struct ListNode‘
项目场景: 做单链表反转题目,报错:member access within null pointer of type ‘struct ListNode’ 题目链接:LINK 问题描述 我明明在初始化指针时候,已经处理了n2->next情况却依然报错 这个报错提示含义是:大概就…...

Qt之Qchar类的接口1
Qt类的构造函数 QChar类提供了许多个不同原型的构造函数,以方便不同场合下使用。 QChar(); //构造一个空字符,即‘\0’ QChar(char ch); //由字符数据ch构造 QChar(uchar ch)…...
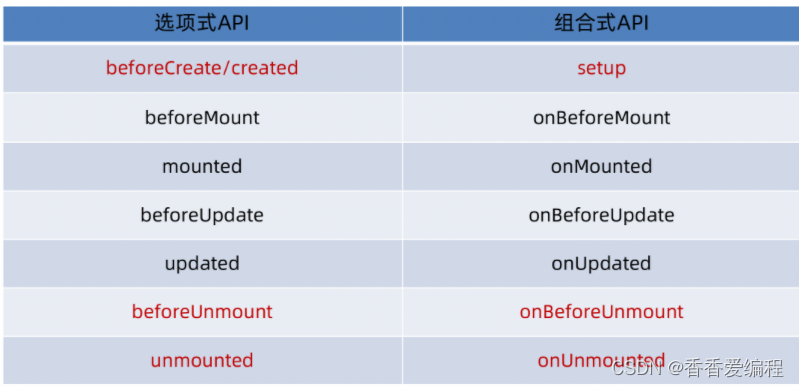
vue的十大面试题详情
1 v-show与v-if区别 v-if与v-show可以根据条件的结果,来决定是否显示指定内容: v-if: 条件不满足时, 元素不会存在. v-show: 条件不满足时, 元素不会显示(但仍然存在). <div id"app"><button click"show !show">点我</but…...
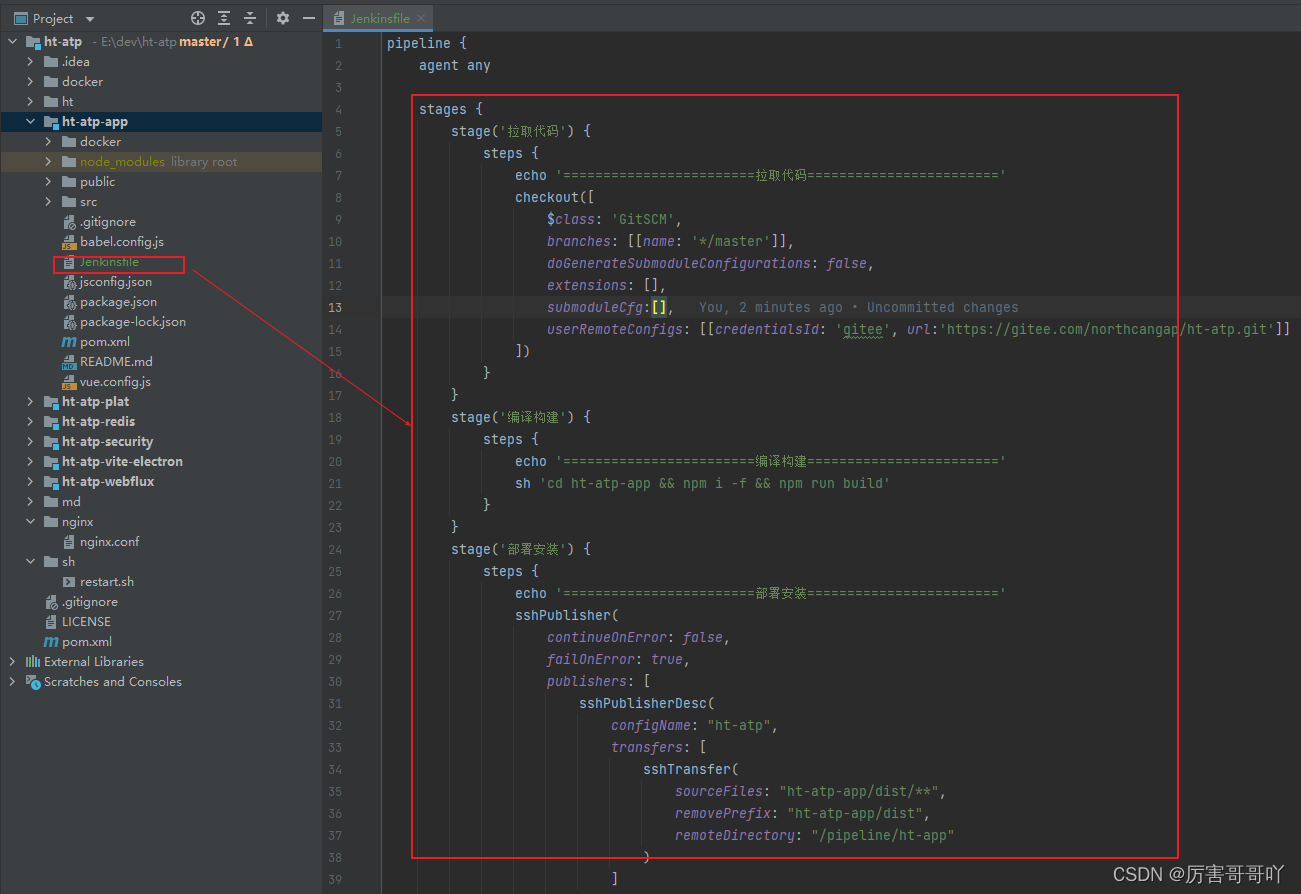
(十四)devops持续集成开发——jenkins流水线使用pipeline方式发布项目
前言 本节内容我们使用另外一种方式pipeline实现项目的流水线部署发布,Jenkins Pipeline是一种允许以代码方式定义持续集成和持续交付流水线的工具。通过Jenkins Pipeline,可以将整个项目的构建、测试和部署过程以脚本的形式写入Jenkinsfile中ÿ…...

多维时序 | Matlab实现LSTM-Mutilhead-Attention长短期记忆神经网络融合多头注意力机制多变量时间序列预测模型
多维时序 | Matlab实现LSTM-Mutilhead-Attention长短期记忆神经网络融合多头注意力机制多变量时间序列预测模型 目录 多维时序 | Matlab实现LSTM-Mutilhead-Attention长短期记忆神经网络融合多头注意力机制多变量时间序列预测模型预测效果基本介绍程序设计参考资料 预测效果 基…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
