【感知算法】Dempster-Shafer理论(下)
尝试DS理论应用到自动驾驶地图众包更新。
地图特征变化判断
a mass function is applied to quantify the evidence of the existence.
existence state: existenct、non-existent、tenative、conflict
∃ ∄ Ω ϕ \exist \\ \not\exist \\ \Omega \\ \phi ∃∃Ωϕ
mass function: quantify the evidence of the existence.
- mass functions of the measurement
m a s s z t ( ∃ ) = λ m a s s z t ( ∄ ) = 0 m a s s z t ( ϕ ) = 0 m a s s z t ( Ω ) = 1 − λ mass_{z_t}( \exist ) = \lambda \\ mass_{z_t}( \not \exist ) = 0 \\ mass_{z_t}( \phi ) = 0 \\ mass_{z_t}( \Omega ) = 1-\lambda masszt(∃)=λmasszt(∃)=0masszt(ϕ)=0masszt(Ω)=1−λ
- mass functions of the non-measurement
m a s s z t ( ∃ ) = 0 m a s s z t ( ∄ ) = λ m a s s z t ( ϕ ) = 0 m a s s z t ( Ω ) = 1 − λ mass_{z_t}( \exist ) = 0 \\ mass_{z_t}( \not \exist ) = \lambda \\ mass_{z_t}( \phi ) = 0 \\ mass_{z_t}( \Omega ) = 1-\lambda masszt(∃)=0masszt(∃)=λmasszt(ϕ)=0masszt(Ω)=1−λ
Inference of the map feature existence based Dempster Combination Rule
- mass functions of map features and new map features
初始化使用第i个地图特征的先验置信度 λ H D \lambda_{HD} λHD
m a s s H D 0 { i } ( ∃ ) = λ H D m a s s H D 0 { i } ( ∄ ) = 0 m a s s H D 0 { i } ( ϕ ) = 0 m a s s H D 0 { i } ( Ω ) = 1 − λ H D mass_{HD_{0\{i\}}}( \exist ) = \lambda_{HD} \\ mass_{HD_{0\{i\}}}( \not \exist ) = 0 \\ mass_{HD_{0\{i\}}}( \phi ) = 0 \\ mass_{HD_{0\{i\}}}( \Omega ) = 1 - \lambda_{HD} massHD0{i}(∃)=λHDmassHD0{i}(∃)=0massHD0{i}(ϕ)=0massHD0{i}(Ω)=1−λHD
新增加的第j个地图特征,按下列式初始化
m a s s n e w 0 { j } ( ∃ ) = 0 m a s s n e w 0 { j } ( ∄ ) = 0 m a s s n e w 0 { j } ( ϕ ) = 0 m a s s n e w 0 { j } ( Ω ) = 1 mass_{new_{0\{j\}}}( \exist ) = 0 \\ mass_{new_{0\{j\}}}( \not \exist ) = 0 \\ mass_{new_{0\{j\}}}( \phi ) = 0 \\ mass_{new_{0\{j\}}}( \Omega ) = 1 \\ massnew0{j}(∃)=0massnew0{j}(∃)=0massnew0{j}(ϕ)=0massnew0{j}(Ω)=1
- Usd Dempster combination rule ⊕ \oplus ⊕ to accumulate the measurement existence m a s s z t mass_{z_t} massztto the each map feature existence at time t − 1 t-1 t−1,
m a s s H D t { i } = m a s s H D t − 1 { i } ⊕ m a s s z t m a s s n e w t { j } = m a s s n e w t − 1 { j } ⊕ m a s s z t mass_{HD_{t\{i\}}} = mass_{HD_{t-1\{i\}}}\oplus mass_{z_t} \\ mass_{new_{t\{j\}}} = mass_{new_{t-1\{j\}}}\oplus mass_{z_t} massHDt{i}=massHDt−1{i}⊕massztmassnewt{j}=massnewt−1{j}⊕masszt
其中,
m a s s 1 ⊕ 2 ( A ) = m a s s 1 ∩ 2 ( A ) 1 − m a s s 1 ∩ 2 ( ϕ ) , ∀ A ⊆ Ω , A ≠ ϕ m a s s 1 ⊕ 2 ( ϕ ) = 0 ∀ A ⊆ Ω , m a s s 1 ∩ 2 ( A ) = ∑ B ∩ C = A ∣ B , C ⊆ Ω m a s s 1 ( B ) m a s s 2 ( C ) mass_{1\oplus2}(A) = \frac{mass_{1\cap2}(A)}{1-mass_{1\cap2}(\phi)}, \forall A\subseteq\Omega,A\neq\phi \\ mass_{1\oplus2}(\phi) = 0 \\ \forall A\subseteq\Omega, mass_{1\cap2}(A) = \sum_{B\cap C=A|B,C\subseteq\Omega}mass_1(B)mass_2(C) mass1⊕2(A)=1−mass1∩2(ϕ)mass1∩2(A),∀A⊆Ω,A=ϕmass1⊕2(ϕ)=0∀A⊆Ω,mass1∩2(A)=B∩C=A∣B,C⊆Ω∑mass1(B)mass2(C)
注:公式 m a s s 1 ⊕ 2 ( A ) mass_{1\oplus2}(A) mass1⊕2(A)即 m a s s 1 ( A ) ⊕ m a s s 2 ( A ) mass_{1}(A)\oplus mass_2(A) mass1(A)⊕mass2(A)
求和条件中的 ∣ | ∣为并列含义, Ω \Omega Ω为超集 2 X 2^X 2X,
∃ ∩ ∃ = ∃ ∃ ∩ Ω = ∃ ∃ ∩ ∄ = ∅ ∅ ∩ ∃ = ∅ ∅ ∩ ∄ = ∅ ∅ ∩ Ω = ∅ ∅ ∩ ∅ = ∅ \exist \cap \exist = \exist\\ \exist \cap \Omega = \exist\\ \exist \cap \not\exist = \emptyset \\ \emptyset \cap \exist = \emptyset \\ \emptyset \cap \not \exist = \emptyset \\ \emptyset \cap \Omega = \emptyset \\ \emptyset \cap \emptyset = \emptyset \\ ∃∩∃=∃∃∩Ω=∃∃∩∃=∅∅∩∃=∅∅∩∃=∅∅∩Ω=∅∅∩∅=∅
集合运算满足交换律。
相关文章:
)
【感知算法】Dempster-Shafer理论(下)
尝试DS理论应用到自动驾驶地图众包更新。 地图特征变化判断 a mass function is applied to quantify the evidence of the existence. existence state: existenct、non-existent、tenative、conflict ∃ ∄ Ω ϕ \exist \\ \not\exist \\ \Omega \\ \phi ∃∃Ωϕ ma…...

通过conda安装cudatoolikit和cudnn
通过conda安装cudatoolikit和cudnn 安装cudatoolkit安装cudnn安装cudatoolkit-dev 安装cudatoolkit conda install cudatoolkit11.3 -c https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ 安装cudnn conda install cudnn8.5 -c https://mirrors.tuna.tsinghua.edu.…...

vue中使用jsx语法
请注意,在 Vue 中使用 JSX 时,你仍然需要通过 h 函数(通常是一个别名,对应于 createElement 函数)来创建虚拟 DOM 元素。在下面的例子中,h 函数作为 render 函数的参数传入,但在 JSX 语法中你通…...
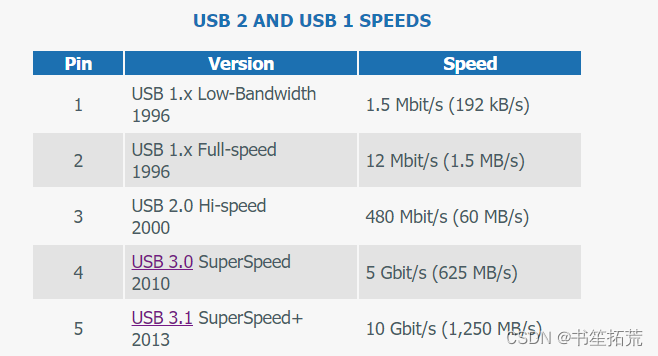
我的NPI项目之Android USB 系列(一) - 遥望和USB的相识
和USB应该是老朋友了,从2011年接触Android开发开始,就天天和USB打交道了。那时候还有不 对称扁头的usb/方口的usb,直到如今使用广泛的防反插USB3.0 type-C。 但是,一直有一个不是很清楚的问题萦绕在心头,那就是。先有…...
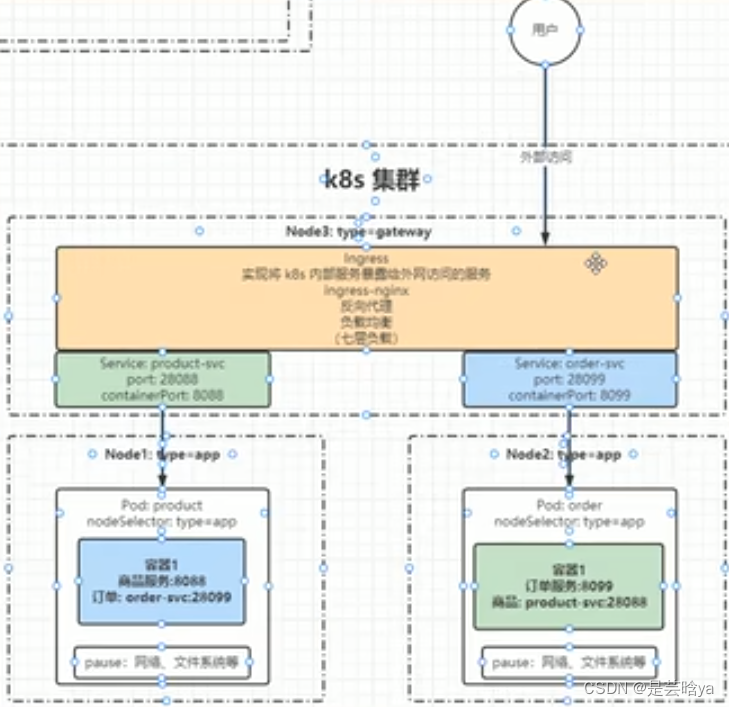
K8s进阶之路-命名空间级-服务发现 :
服务发现: Service(东西流量):集群内网络通信、负载均衡(四层负载)内部跨节点,节点与节点之间的通信,以及pod与pod之间的通信,用Service暴露端口即可实现 Ingress&#…...

智慧公厕管理系统:让城市智慧驿站更加智慧舒适
智慧公厕管理系统是城市智慧驿站中不可或缺的一部分,它通过全方位的信息化解决方案,为公共厕所的使用、运营和管理提供了一种智能化的方式。作为城市智慧驿站的重要组成部分,智慧公厕管理系统发挥着重要的作用,为城市社会民生提供…...
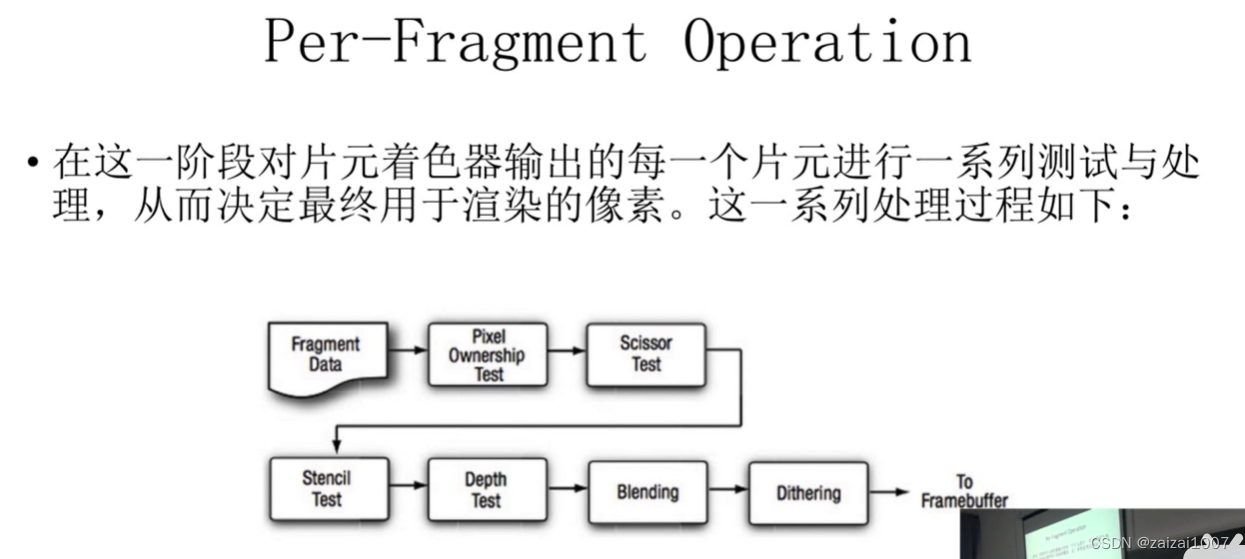
图形渲染基础学习
原文链接:游戏开发入门(三)图形渲染_如果一个面只有三个像素进行渲染可以理解为是定点渲染吗?-CSDN博客 游戏开发入门(三)图形渲染笔记: 渲染一般分为离线渲染与实时渲染,游戏中我们用的都是…...

每日学习总结20240219
每日总结 20240219 1.文件类型.csv CSV文件是一种以逗号分隔值(Comma-Separated Values)为标记的文本文件,它可以用来存储表格数据。每一行表示一条记录,而每一条记录中的字段则使用逗号或其他特定的分隔符进行分隔。 常用场景…...

K8s进阶之路-安装部署K8s
参考:(部署过程参考的下面红色字体文档链接就可以,步骤很详细,重点部分在下面做了标注) 安装部署K8S集群文档: 使用kubeadm方式搭建K8S集群 GitBook 本机: master:10.0.0.13 maste…...
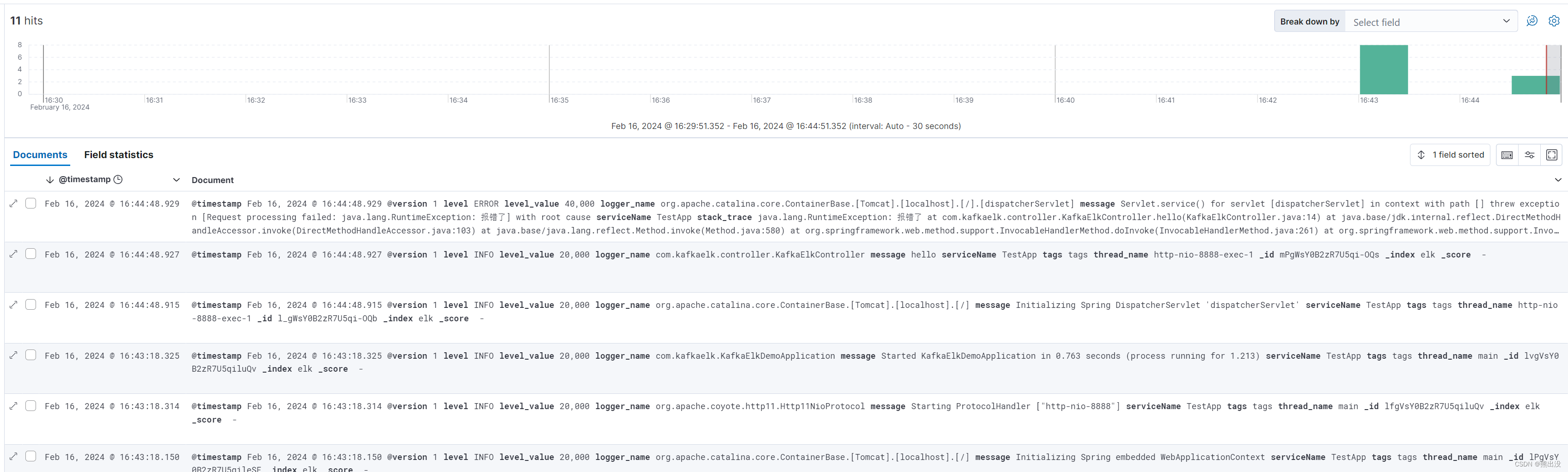
springboot集成elk实现日志采集可视化
一、安装ELK 安装ELK组件请参考我这篇博客:windows下安装ELK(踩坑记录)_windows上安装elk教程-CSDN博客 这里不再重复赘述。 二、编写logstash配置 ELK组件均安装好并成功启动,进入到logstash组件下的config文件夹,创建logstash.conf配置…...

leetcode 148. 排序链表 java解法
Problem: 148. 排序链表 思路 这是一个链表排序的问题,由于要求时间复杂度为 O(nlogn),适合使用归并排序(Merge Sort)来解决。 解题方法 首先,使用快慢指针找到链表的中间节点,将链表分成两部分。然后&…...
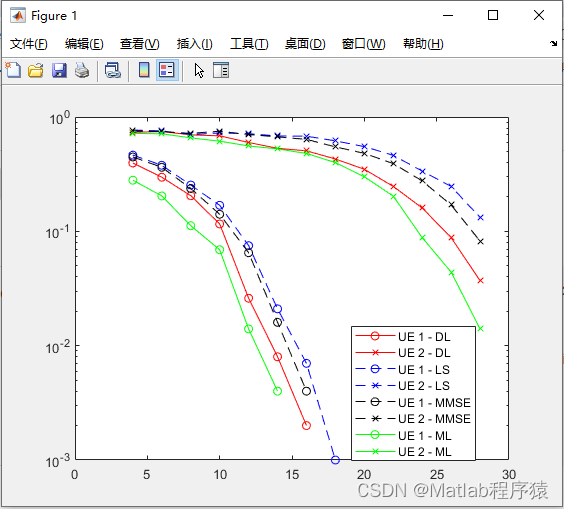
【MATLAB源码-第140期】基于matlab的深度学习的两用户NOMA-OFDM系统信道估计仿真,对比LS,MMSE,ML。
操作环境: MATLAB 2022a 1、算法描述 深度学习技术在无线通信领域的应用越来越广泛,特别是在非正交多址接入(NOMA)和正交频分复用(OFDM)系统中,深度学习技术被用来提高信道估计的性能和效率。…...

运动重定向学习笔记
目录 深度学习 重定向 2020年的模型: 重定向之后的bvh: 深度学习 重定向 输入是bvh,输出也是bvh...

导出Excel,支持最佳
列表信息导出为Excel文件, 依赖pom: Sheet, Row:<dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId> </dependency>XSSFWorkbook <dependency><groupId>org.apache.poi</…...

【WPF】获取父控件数据
MaxHeight"{Binding PathActualHeight, RelativeSource{RelativeSource ModeFindAncestor, AncestorTypeUserControl}}" 参考文献 https://www.cnblogs.com/-Timosthetic/p/16021865.html...
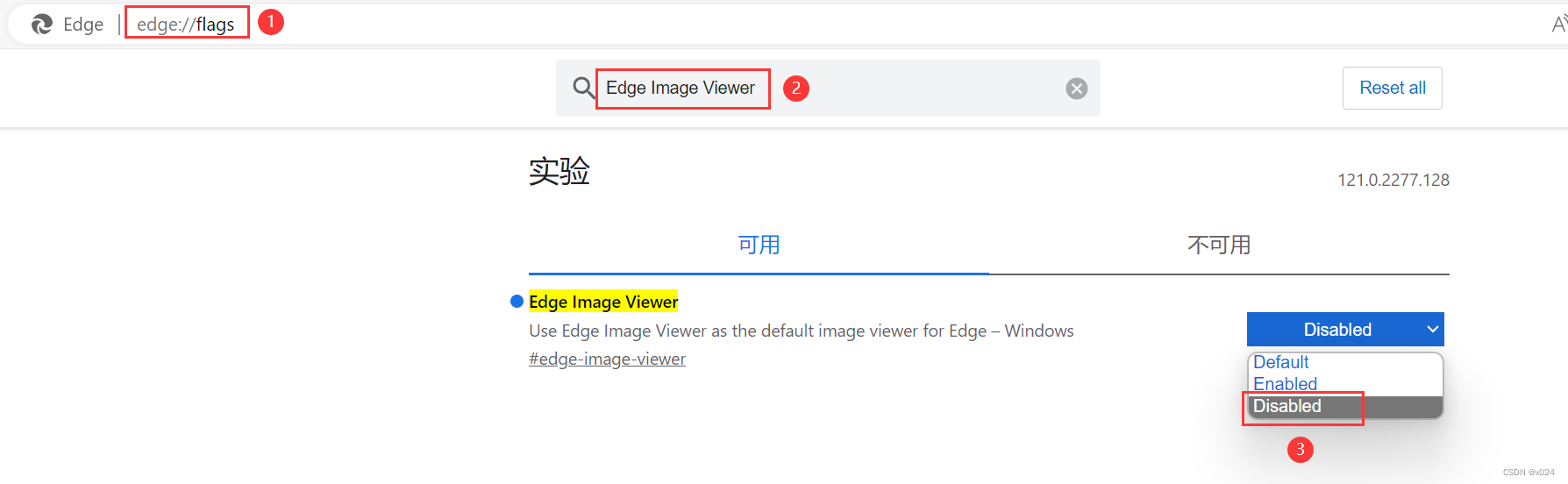
解决Edge浏览器,微博无法查看大图(Edge Image Viewer)
使用Edge浏览器浏览微博或其它带校验的图片时,会导致无法查看。 主要原因为Edge自带了一个Edge Image Viewer, 但是该图片查看器无法查看带校验数据的图片,所以导致查看时一片空白。 解决方法 地址栏输入 edge://flags/搜索 Edge Image Viewer选择 Disa…...
PMP含金量在国内怎么样?
其一、PMP(项目管理师)证书含金量高吗? PMP认证是由美国项目管理学会(PMI)在全球范围内推出的针对项目经理的资格认证体系,其证书含金量可以说是非常高。 统计表明,全球年销售收入在5亿美元以上的企业中有86%聘用了具有项目管理资质的项目经…...
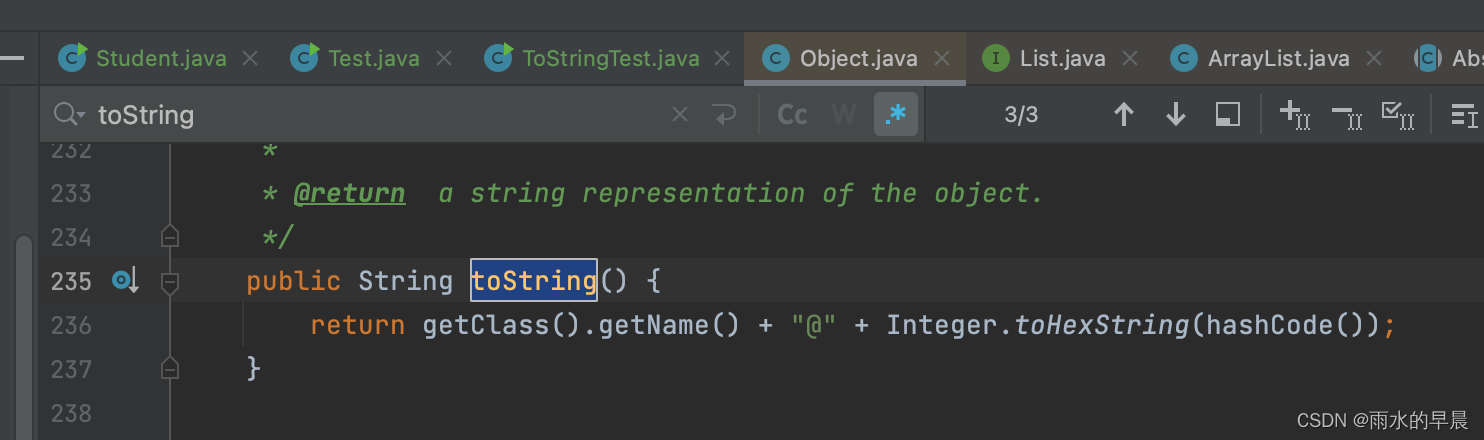
java中容易被忽视的toString()方法
之前一直认为toString就是将数据转换成字符类型,直到最近写出了一个bug才对toString有了新的认识 不同数据类型,toString() 有不同的操作 定义一个student类,包含姓名 String类型、性别 String类型、年龄 int 类型、分数列表 String类型的li…...
如何使用Docker搭建YesPlayMusic网易云音乐播放器并发布至公网访问
文章目录 1. 安装Docker2. 本地安装部署YesPlayMusic3. 安装cpolar内网穿透4. 固定YesPlayMusic公网地址 本篇文章讲解如何使用Docker搭建YesPlayMusic网易云音乐播放器,并且结合cpolar内网穿透实现公网访问音乐播放器。 YesPlayMusic是一款优秀的个人音乐播放器&am…...
java面试题之redis篇
1.redis 中的数据类型有哪些 随着 Redis 版本的更新,后面又支持了四种数据类型: BitMap(2.2 版新增)、HyperLogLog(2.8 版新增)、GEO(3.2 版新增)、Stream(5.0 版新增&am…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
