备战蓝桥杯 Day5
1191:流感传染
【题目描述】
有一批易感人群住在网格状的宿舍区内,宿舍区为n*n的矩阵,每个格点为一个房间,房间里可能住人,也可能空着。在第一天,有些房间里的人得了流感,以后每天,得流感的人会使其邻居传染上流感,(已经得病的不变),空房间不会传染。请输出第m天得流感的人数。
【输入】
第一行一个数字n,n不超过100,表示有n*n的宿舍房间。
接下来的n行,每行n个字符,’.’表示第一天该房间住着健康的人,’#’表示该房间空着,’@’表示第一天该房间住着得流感的人。
接下来的一行是一个整数m,m不超过100。
【输出】
输出第m天,得流感的人数。
【输入样例】
5 ....# .#.@. .#@.. #.... ..... 4【输出样例】
16
#include<iostream>
using namespace std;
const int N = 1e2 + 10;
char a[N][N];//房间数组
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
bool vis[N][N];//标记当天生病的
int main()
{int n; cin >> n;//存储房间for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){cin >> a[i][j];}}//记录生病的人数int cnt=0;int m;cin >> m;//开始感染for (int day = 2; day <= m; day++){memset(vis,0,sizeof vis);for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){if (a[i][j] == '@'&&!vis[i][j]) {//遍历所有可能感染的方向for (int k = 0; k < 4; k++){int bx = i + dx[k], by = j + dy[k];//超出房间的边界if (i<1 || i>n || j<1 || j>n)continue;if (a[bx][by] == '.') {a[bx][by] = '@';//标记当天被感染的vis[bx][by] = 1;}}}}}}for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){if (a[i][j] == '@')cnt++;}}cout << cnt;return 0;
}
1314:【例3.6】过河卒(Noip2002)
|
#include<iostream>
using namespace std;
#define int long long
const int N = 1e2 + 10;
int a[N][N];
//马可走的八个方向
int dx[] = {1,1,-1,-1,2,2,-2,-2};
int dy[] = {2,-2,2,-2,1,-1,1,-1};
bool vis[N][N];//马运动的轨迹
/*
//边界
a[i][j]=1
//递推关系式
a[i][j]=a[i-1][j]+a[i][j-1]
*/
signed main()
{int tx, ty;//B点坐标int cx, cy;//C点坐标cin >> tx >> ty >> cx >> cy;vis[cx][cy] = 1;//标记马//马运动的轨迹for (int i = 0; i < 8; i++){int cxx = cx + dx[i], cyy = cy + dy[i];//如果新生成的坐标越界,则跳过,继续生成下一个坐标if (cxx<0 || cxx>tx || cyy<0 || cyy>ty)continue;//0也是边界vis[cxx][cyy] = 1;}//边界a[0][0] = 1;//处理第一行for (int j = 1; j <= ty; j++){if (!vis[0][j])a[0][j] = a[0][j - 1];elsea[0][j] = 0;}//处理第一列for (int i = 1; i <= tx; i++){if (!vis[i][0])a[i][0] = a[i - 1][0];elsea[i][0] = 0;}//递推for (int i = 1; i <= tx; i++){for (int j = 1; j <= ty; j++){if (!vis[i][j])a[i][j] = a[i - 1][j] + a[i][j - 1];elsea[i][j] = 0;}}cout << a[tx][ty] << endl;return 0;
}1194:移动路线
【题目描述】
X桌子上有一个m行n列的方格矩阵,将每个方格用坐标表示,行坐标从下到上依次递增,列坐标从左至右依次递增,左下角方格的坐标为(1,1),则右上角方格的坐标为(m,n)。
小明是个调皮的孩子,一天他捉来一只蚂蚁,不小心把蚂蚁的右脚弄伤了,于是蚂蚁只能向上或向右移动。小明把这只蚂蚁放在左下角的方格中,蚂蚁从
左下角的方格中移动到右上角的方格中,每步移动一个方格。蚂蚁始终在方格矩阵内移动,请计算出不同的移动路线的数目。
对于1行1列的方格矩阵,蚂蚁原地移动,移动路线数为1;对于1行2列(或2行1列)的方格矩阵,蚂蚁只需一次向右(或向上)移动,移动路线数也为1……对于一个2行3列的方格矩阵,如下图所示:
(2,1) (2,2) (2,3) (1,1) (1,2) (1,3) 蚂蚁共有3种移动路线:
路线1:(1,1) → (1,2) → (1,3) → (2,3)
路线2:(1,1) → (1,2) → (2,2) → (2,3)
路线3:(1,1) → (2,1) → (2,2) → (2,3)
【输入】
输入只有一行,包括两个整数m和n(0 < m+n ≤ 20),代表方格矩阵的行数和列数,m、n之间用空格隔开。
【输出】
输出只有一行,为不同的移动路线的数目。
【输入样例】
2 3【输出样例】
3
#include<iostream>
using namespace std;
#define int long long
const int N = 1e2 + 10;
int a[N][N];
signed main()
{int n, m;cin >> n >> m;//处理边界a[1][1] = 1;//处理第一行for (int j = 2; j <= m; j++)a[1][j] = a[1][j-1];//处理其余路线for (int i = 2; i <= n; i++)a[i][1] = a[i - 1][1];for (int i = 2; i <= n; i++)for (int j = 2; j <= m; j++)a[i][j] = a[i][j - 1] + a[i - 1][j];cout << a[n][m];return 0;
} 1196:踩方格
|
#include<iostream>
using namespace std;
#define int long long
const int N = 1e2 + 10;
int a[N][N];
int l[N], r[N], u[N];//向左 右 上 的方案总数
signed main()
{int n; cin >> n;l[1] = r[1] = u[1] = 1;/*若i-1步向左,那么第i部只能向上或者向左若i-1步向右,那么第i部只能向上或者向右若i-1步向上,那么第i部能向上或者向左或者向右*/int ans = 0;//记录方案数for (int i = 2; i <= n; i++){l[i] = u[i - 1] + l[i - 1];r[i] = u[i - 1] + r[i - 1];u[i] = u[i - 1] + l[i - 1] + r[i - 1];ans = l[i] + r[i] + u[i];}cout << ans;return 0;
}1313:【例3.5】位数问题
【题目描述】
在所有的N�位数中,有多少个数中有偶数个数字33?由于结果可能很大,你只需要输出这个答案对1234512345取余的值。
【输入】
读入一个数N(N≤1000)�(�≤1000)。
【输出】
输出有多少个数中有偶数个数字33。
【输入样例】
2【输出样例】
73
#include<iostream>
using namespace std;
#define int long long
/*
1位数 2位数 3位数 4位数even[1] odd[1] even[2] odd[2] even[3] odd[3] even[4] odd[4]
0 3 9*even[1]+odd[1] 9*odd[1]+even[1] 9*even[2]+odd[2] 9*odd[2]+even[2] 8*even[3]+odd[3] 8*odd[3]+even[3]
1
2
4
5
6
7
8
9
*/
const int N = 1e3 + 10, mod = 12345;
int even[N], odd[N];
signed main() {even[1] = 9; odd[1] = 1;int n; cin >> n;int t = 9;for (int i = 2; i <= n; i++) {if (i == n) t = 8;//当走到最高位时,最高位不能为0,方案少一种变为8odd[i] = (t * odd[i - 1] % mod + even[i - 1] % mod) % mod;even[i] = (t * even[i - 1] % mod + odd[i - 1] % mod) % mod;}cout << even[n] << endl;return 0;
}1201:菲波那契数列
【题目描述】
菲波那契数列是指这样的数列: 数列的第一个和第二个数都为1,接下来每个数都等于前面2个数之和。
给出一个正整数a,要求菲波那契数列中第a个数是多少。
【输入】
第1行是测试数据的组数n,后面跟着n行输入。每组测试数据占1行,包括一个正整数a(1<=a<=20)。
【输出】
输出有n行,每行输出对应一个输入。输出应是一个正整数,为菲波那契数列中第a个数的大小。
【输入样例】
4 5 2 19 1【输出样例】
5 1 4181 1
#include<iostream>
using namespace std;
const int N=1e2+10;
int fbnq(int x)
{if (x <= 2)return 1;return fbnq(x - 1) + fbnq(x - 2);
}
int main()
{int n; cin >> n;int x;while (n--){cin >> x;cout << fbnq(x) << endl;;}return 0;
}1202:Pell数列
【题目描述】
Pell数列a1,a2,a3,...�1,�2,�3,...的定义是这样的,a1=1,a2=2,...,an=2an−1+an−2(n>2)�1=1,�2=2,...,��=2��−1+��−2(�>2)。
给出一个正整数 k�,要求Pell数列的第 k� 项模上 3276732767 是多少。
【输入】
第1行是测试数据的组数 n�,后面跟着 n� 行输入。每组测试数据占 11 行,包括一个正整数k(1≤k<1000000)�(1≤�<1000000)。
【输出】
n� 行,每行输出对应一个输入。输出应是一个非负整数。
【输入样例】
2 1 8【输出样例】
1 408
#include<iostream>
using namespace std;
const int N=1e6+10;
#define int long long
int m = 32767;
int a[N];
int pell(int x)
{//剪枝(求过的项不需要重复求)if (a[x])return a[x];if (x <= 2)return a[x]=x;return a[x]=(2 * pell(x - 1) % m + pell(x - 2) % m) % m;
}
signed main()
{int n; cin >> n;int x;while (n--){cin >> x;cout << pell(x) << endl;;}return 0;
}1204:爬楼梯
【题目描述】
树老师爬楼梯,他可以每次走1级或者2级,输入楼梯的级数,求不同的走法数。
例如:楼梯一共有3级,他可以每次都走一级,或者第一次走一级,第二次走两级,也可以第一次走两级,第二次走一级,一共3种方法。
【输入】
输入包含若干行,每行包含一个正整数N,代表楼梯级数,1≤N≤30。
【输出】
不同的走法数,每一行输入对应一行输出。
【输入样例】
5 8 10【输出样例】
8 34 89
#include<iostream>
using namespace std;
const int N=1e2+10;
#define int long long
int a[N];
int stairs(int x)
{/*s(8) a[8]=s(7)+s(6)=34s(7) a[7]=s(6)+s(5)=21s(6) a[6]=s(5)+s(4)=13s(5) a[5]=s(4)+s(3)=8s(4) a[4]=s(3)+s(2)=5 s(3) a[3]=s(2)+s(1)=3 *///剪枝if (a[x])return a[x];if (x <= 2)return a[x] = x;return a[x]=stairs(x - 1) + stairs(x - 2);
}
signed main()
{int x;while (cin >> x){cout << stairs(x)<< endl;}return 0;
}
相关文章:
备战蓝桥杯 Day5
1191:流感传染 【题目描述】 有一批易感人群住在网格状的宿舍区内,宿舍区为n*n的矩阵,每个格点为一个房间,房间里可能住人,也可能空着。在第一天,有些房间里的人得了流感,以后每天,得…...
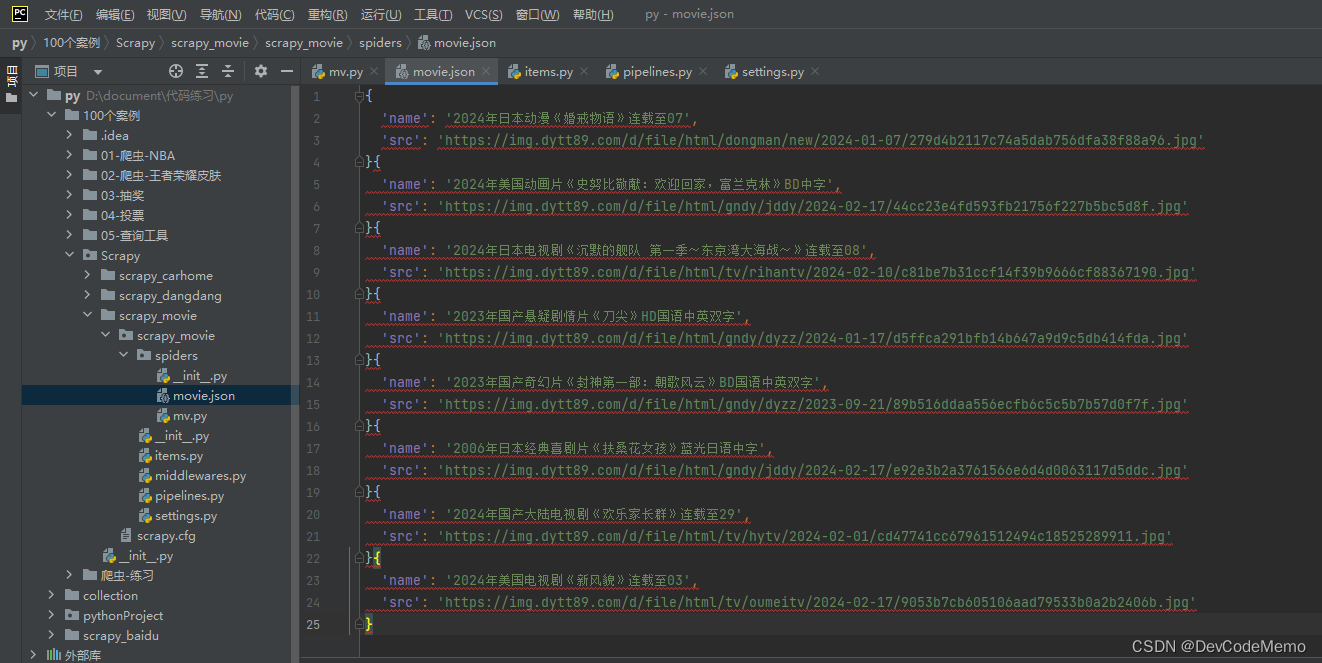
爬虫学习笔记-scrapy爬取电影天堂(双层网址嵌套)
1.终端运行scrapy startproject movie,创建项目 2.接口查找 3.终端cd到spiders,cd scrapy_carhome/scrapy_movie/spiders,运行 scrapy genspider mv https://dy2018.com/ 4.打开mv,编写代码,爬取电影名和网址 5.用爬取的网址请求,使用meta属性传递name ,callback调用自定义的…...

Unity笔记:数据持久化的几种方式
正文 主要方法: ScriptableObjectPlayerPrefsJSONXML数据库(如Sqlite) 1. PlayerPerfs PlayerPrefs 存储的数据是全局共享的,它们存储在用户设备的本地存储中,并且可以被应用程序的所有部分访问。这意味着…...
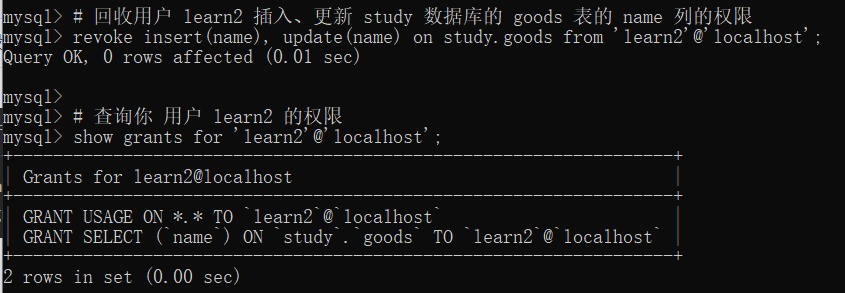
MySQL 基础知识(八)之用户权限管理
目录 1 MySQL 权限管理概念 2 用户管理 2.1 创建用户 2.2 查看当前登录用户 2.3 修改用户名 2.4 删除用户 3 授予权限 3.1 授予用户管理员权限 3.2 授予用户数据库权限 3.3 授予用户表权限 3.4 授予用户列权限 4 查询权限 5 回收权限 1 MySQL 权限管理概念 关于 M…...
QT编写工具基本流程(自用)
以后有人让你写工具的时候,可以方便用这个模版及时提高工作效率,可以争取早点下班。包含库目录,头文件目录,输出目录以及翻译和部署,基本上都全了,也可以做收藏用用。 文章目录 1、创建项目Dialog Widget都…...
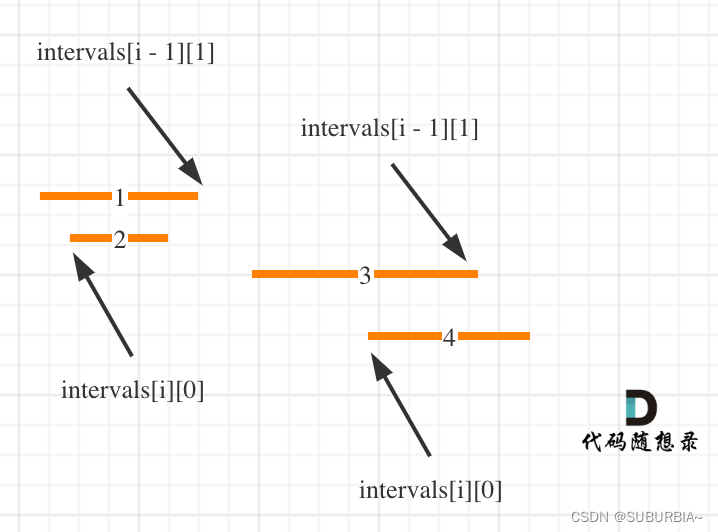
代码随想录算法训练营第三六天 | 无重叠区间、划分字母区间、合并区间
目录 无重叠区间划分字母区间合并区间 LeetCode 435. 无重叠区间 LeetCode 763.划分字母区间 LeetCode 56. 合并区间 无重叠区间 给定一个区间的集合 intervals ,其中 intervals[i] [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠…...

DP读书:《openEuler操作系统》(十)套接字 Socket 数据传输的基本模型
10min速通Socket 套接字简介数据传输基本模型1.TCP/IP模型2.UDP模型 套接字类型套接字(Socket)编程Socket 的连接1.连接概述(1)基本概念(2)连接状态(3)连接队列 2.建立连接3.关闭连接 socket 编程接口介绍数据的传输1. 阻塞与非阻塞2. I/O复用 数据的传输…...
抓住母亲节销售机会:Shopee 平台选品策略大揭秘
母亲节,作为一个重要的购物节日,为卖家带来了巨大的销售机会。在Shopee这样的电商平台上,如何通过有效的选品策略吸引消费者、提高销量呢?下面将介绍一些关键策略,帮助卖家在母亲节期间实现销售突破。 先给大家推荐一…...

Mysql如何优化数据查询方案
mysql做读写分离 读写分离是提高mysql并发的首选方案。 Mysql主从复制的原理 mysql的主从复制依赖于binlog,也就是记录mysql上的所有变化并以二进制的形式保存在磁盘上,复制的过程就是将binlog中的数据从主库传输到从库上。 主从复制过程详细分为3个阶段…...

SwiftUI 更自然地向自定义视图传递参数的“另类”方式
概览 在 SwiftUI 中,正是自定义视图让我们的 App 变得与众不同!然而,除了传统的视图接口定义方式以外,我们其实还可以有更“银杏化”的选择。 如上图所示:对于 SubView 子视图所需的参数我们一开始并没有操之过急&…...

Word第一课
文章目录 1. 文件格式1.1 如何显示文件扩展名1.2 Word文档格式的演变1.3 常见的Word文档格式 3. 文档属性理解文档属性查看文档属性 1. 文件格式 1.1 如何显示文件扩展名 文档格式指的是文件的扩展名,例如下图 对于该文件,.docx就是文件扩展名&#x…...

【Vue3】路由传参的几种方式
路由导航有两种方式,分别是:声明式导航 和 编程式导航 参数分为query参数和params参数两种 声明式导航 query参数 一、路径字符串拼接(不推荐) 1.传参 在路由路径后直接拼接?参数名:参数值 ,多组参数间使用&分隔。 <RouterLink …...
))
突破编程_C++_面试(高级特性(1))
面试题1:什么是线程以及它在并发编程中的作用是什么 线程( Thread )是操作系统能够进行运算调度的最小单位,它被包含在进程之中,是进程中的实际运作单位。一条线程指的是进程中一个单一顺序的控制流,一个进…...
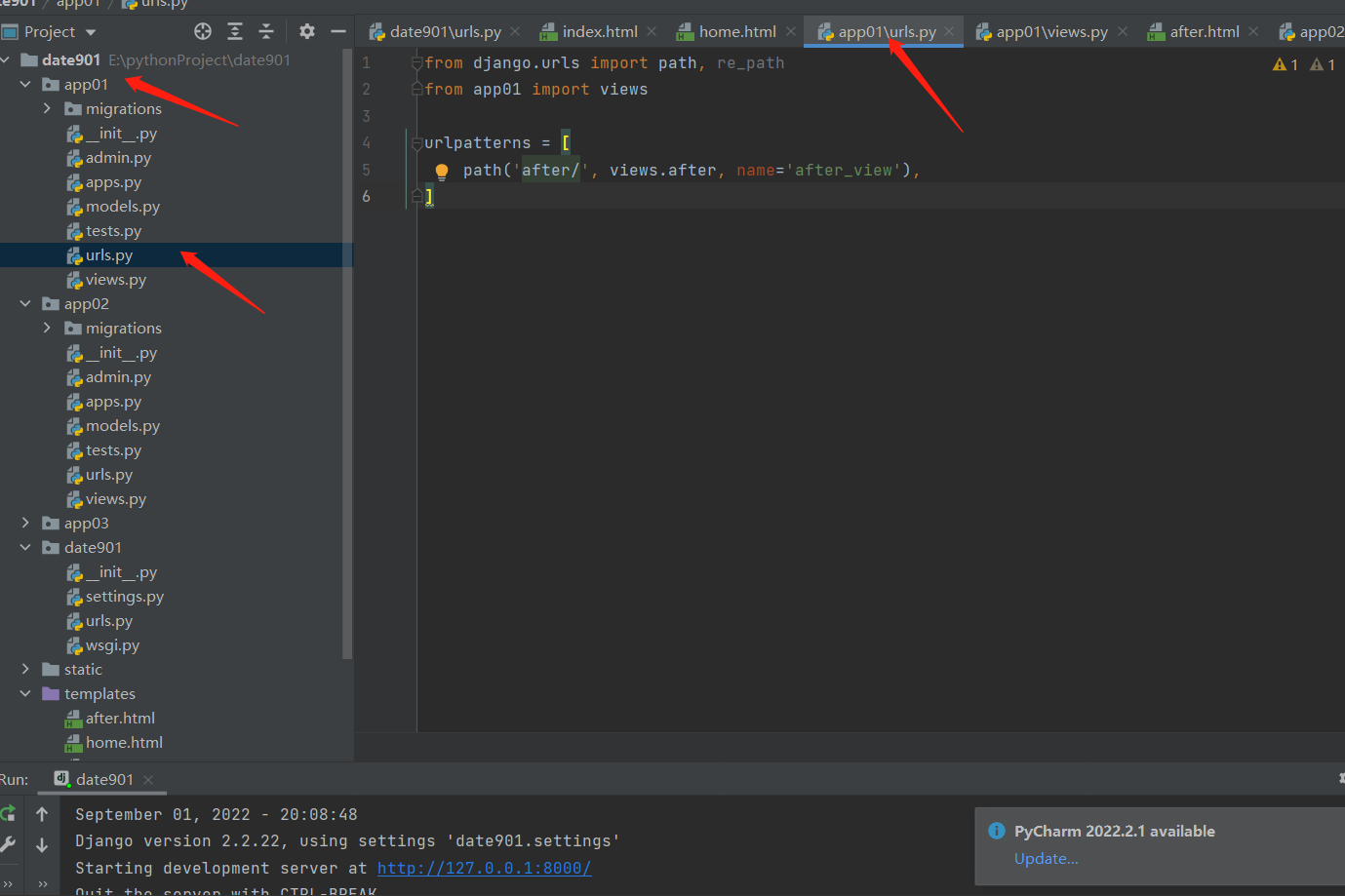
django请求生命周期流程图,路由匹配,路由有名无名反向解析,路由分发,名称空间
django请求生命周期流程图 浏览器发起请求。 先经过网关接口,Django自带的是wsgiref,请求来的时候解析封装,响应走的时候打包处理,这个wsgiref模块本身能够支持的并发量很少,最多1000左右,上线之后会换成u…...
|Day54(动态规划))
@ 代码随想录算法训练营第8周(C语言)|Day54(动态规划)
代码随想录算法训练营第8周(C语言)|Day54(动态规划) Day53、动态规划(包含题目 ● 123.买卖股票的最佳时机III ● 188.买卖股票的最佳时机IV ) 123.买卖股票的最佳时机III 题目描述 给定一个数组&#…...

Flask 学习100-Flask-SocketIO 结合 xterm.js 实现网页版Xshell
前言 xterm.js 是一个使用 TypeScript 编写的前端终端组件,可以直接在浏览器中实现一个命令行终端应用。 可以实现 web-terminal 功能,类似于Xshell 操作服务器。 Flask-SocketIO 快速入门与使用基础参考前面这篇https://www.cnblogs.com/yoyoketang/p/18022139 前后端交互…...

Springboot AOP开发
Springboot AOP开发 一 AOP概述 AOP,即面向切面编程,简言之,面向方法编程。 针对方法,在方法的执行前或执行后使用,用于增强方法,或拓展。 二 AOP开发 1.引入 spring-boot-starter-aop 在SpringBoot项…...

office的excel中使用,告诉我详细的解决方案,如何变成转化为金额格式
在Office的Excel中,如果你想将名为"MEREFIELD"的公式结果转换为金额格式,你可以遵循以下详细步骤来实现: 书写MEREFIELD公式: 首先,在Excel中输入或确认你的MEREFIELD公式。例如,假设这个公式是用…...
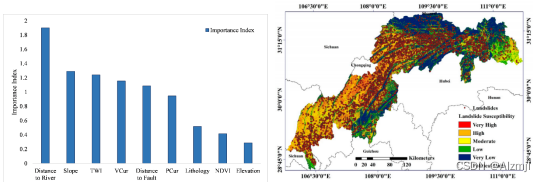
灾后重建中GIS技术的关键作用与案例分析
地质灾害是指全球地壳自然地质演化过程中,由于地球内动力、外动力或者人为地质动力作用下导致的自然地质和人类的自然灾害突发事件。由于降水、地震等自然作用下,地质灾害在世界范围内频繁发生。我国除滑坡灾害外,还包括崩塌、泥石流、地面沉…...
java环境安装
java环境安装 一、官网下载: jdk,下载jdk,解压到D:\JAVA\Java\jdk目录下。 二、配置: 配置环境变量 鼠标右键我的电脑->属性->高级系统设置->环境变量->系统变量新建变量名JAVA_HOME,变量值为刚才解压的…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
