OSQP文档学习
OSQP官方文档
1 QSQP简介
OSQP求解形式为的凸二次规划:

x ∈ R n x∈R^n x∈Rn:优化变量
P ∈ S + n P∈S^n_+ P∈S+n:半正定矩阵
特征
(1)高效:使用了一种自定义的基于ADMM的一阶方法,只需要在设置阶段进行单个矩阵分解。
(2)鲁棒:该算法设置之后不需要对问题数据进行假设(问题只需要是凸的)。
(3)原始/对偶不可行问题:当问题是原始或对偶不可行时,OSQP会检测到它。这是第一个基于一阶方法的QP求解器。
(4)可嵌入:有一个简单的接口来生成定制的可嵌入C代码,而不需要内存管理器。
(5)不需要外部库即可运行
(6)可以很容易地进行热启动,并且可以缓存矩阵分解,以非常有效地解决参数化问题
(7)接口:提供了到C、C++、Fortran、Julia、Matlab、Python、R、Ruby和Rust的接口
2 OSQP求解器

求解器运行以下ADMM算法:

Π \Pi Π:投影到超盒上 [ l , u ] [l,u] [l,u], ρ \rho ρ是ADMM步长
Linear system solution
线性系统解是算法的核心部分。它可以使用直接或间接的方法来完成。
使用直接线性系统求解器,我们求解以下具有拟定矩阵的线性系统:
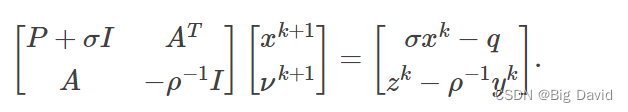
使用间接线性系统求解器,我们求解以下具有正定矩阵的线性系统:
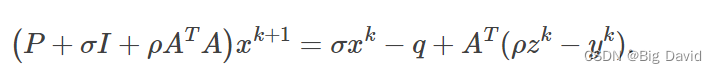
OSQP核心旨在支持不同的线性系统求解器。
Convergence
在每k次迭代时,OSQP生成一个元组 ( x k , z k , y k ) (x^k,z^k,y^k) (xk,zk,yk),
x k ∈ R n , z k 、 y k ∈ R m x^k∈R^n,z^k、y^k∈R^m xk∈Rn,zk、yk∈Rm
与 ( x k , z k , y k ) (x^k,z^k,y^k) (xk,zk,yk)相关的原始残差和对偶残差:



不可行问题
OSQP能够检测问题是原始不可行还是对偶不可行。

3 Get started
安装:
Linux操作系统,默认gcc,cmake已经安装好
① 克隆存储库
git clone https://github.com/osqp/osqp
② 创建目录和更改目录build
cd osqp
mkdir build
cd build
③ 创建 Makefile
cmake -G "Unix Makefiles" ..
④ 编译 OSQP
cmake --build .
C语言:
在 CMake 项目中包括 OSQP,具体取决于您需要共享库还是静态库:
# Find OSQP library and headers
find_package(osqp REQUIRED)# Link the OSQP shared library
target_link_libraries(yourTarget PRIVATE osqp::osqp)# or...# Link the OSQP static library
target_link_libraries(yourTarget PRIVATE osqp::osqpstatic)
4 接口
OSQP有几个接口。以下链接中显示了有关设置、状态值以及如何指定不同线性系统解算器的信息
Solver settings
Linear Systems Solvers
Status values
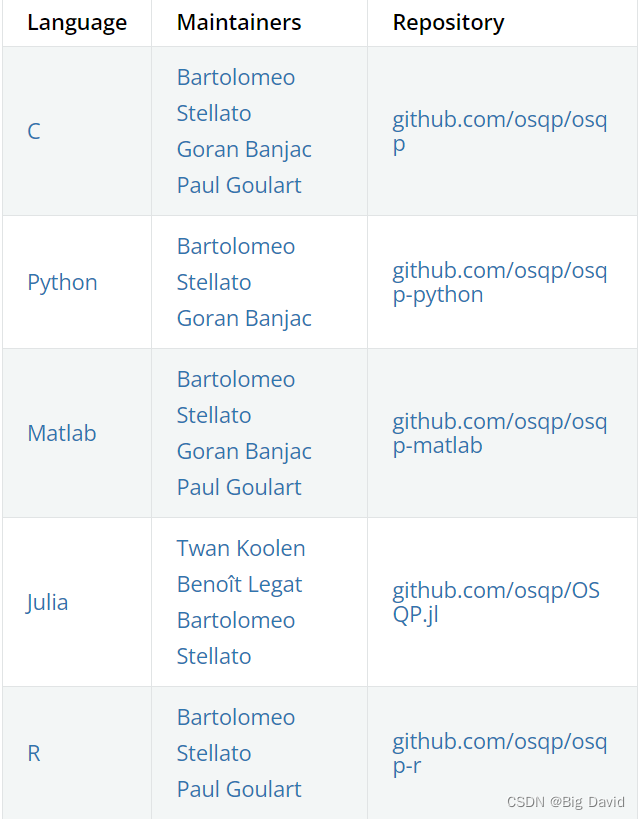
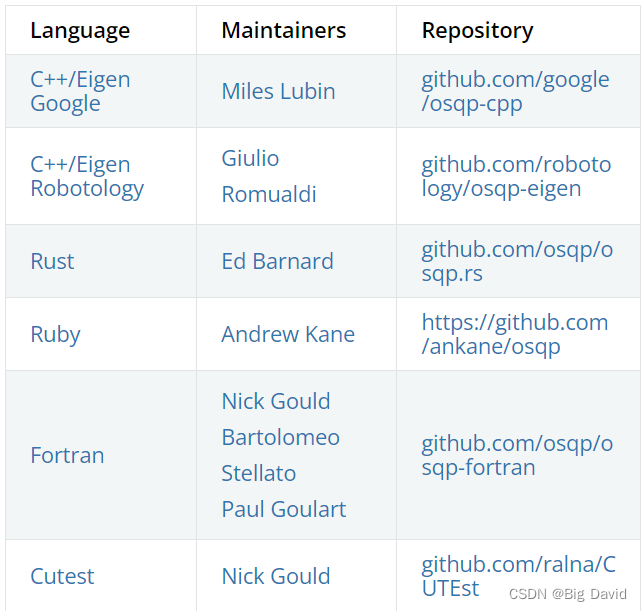
C:github.com/osqp/osqp
C++:github.com/robotology/osqp-eigen
5 Examples
Demo:
① Setup and solve :设置和求解

C:
#include <stdlib.h>
#include "osqp.h"int main(int argc, char **argv) {/* Load problem data */OSQPFloat P_x[3] = {4.0, 1.0, 2.0, };OSQPInt P_nnz = 3;OSQPInt P_i[3] = {0, 0, 1, };OSQPInt P_p[3] = {0, 1, 3, };OSQPFloat q[2] = {1.0, 1.0, };OSQPFloat A_x[4] = {1.0, 1.0, 1.0, 1.0, };OSQPInt A_nnz = 4;OSQPInt A_i[4] = {0, 1, 0, 2, };OSQPInt A_p[3] = {0, 2, 4, };OSQPFloat l[3] = {1.0, 0.0, 0.0, };OSQPFloat u[3] = {1.0, 0.7, 0.7, };OSQPInt n = 2;OSQPInt m = 3;/* Exitflag */OSQPInt exitflag = 0;/* Solver, settings, matrices */OSQPSolver *solver;OSQPSettings *settings;OSQPCscMatrix* P = malloc(sizeof(OSQPCscMatrix));OSQPCscMatrix* A = malloc(sizeof(OSQPCscMatrix));/* Populate matrices */csc_set_data(A, m, n, A_nnz, A_x, A_i, A_p);csc_set_data(P, n, n, P_nnz, P_x, P_i, P_p);/* Set default settings */settings = (OSQPSettings *)malloc(sizeof(OSQPSettings));if (settings) {osqp_set_default_settings(settings);settings->alpha = 1.0; /* Change alpha parameter */}/* Setup solver */exitflag = osqp_setup(&solver, P, q, A, l, u, m, n, settings);/* Solve problem */if (!exitflag) exitflag = osqp_solve(solver);/* Cleanup */osqp_cleanup(solver);if (A) free(A);if (P) free(P);if (settings) free(settings);return (int)exitflag;
};
② Update vectors:更新向量

#include <stdlib.h>
#include "osqp.h"int main(int argc, char **argv) {/* Load problem data */OSQPFloat P_x[3] = {4.0, 1.0, 2.0, };OSQPInt P_nnz = 3;OSQPInt P_i[3] = {0, 0, 1, };OSQPInt P_p[3] = {0, 1, 3, };OSQPFloat q[2] = {1.0, 1.0, };OSQPFloat q_new[2] = {2.0, 3.0, };OSQPFloat A_x[4] = {1.0, 1.0, 1.0, 1.0, };OSQPInt A_nnz = 4;OSQPInt A_i[4] = {0, 1, 0, 2, };OSQPInt A_p[3] = {0, 2, 4, };OSQPFloat l[3] = {1.0, 0.0, 0.0, };OSQPFloat l_new[3] = {2.0, -1.0, -1.0, };OSQPFloat u[3] = {1.0, 0.7, 0.7, };OSQPFloat u_new[3] = {2.0, 2.5, 2.5, };OSQPInt n = 2;OSQPInt m = 3;/* Exitflag */OSQPInt exitflag = 0;/* Solver, settings, matrices */OSQPSolver *solver;OSQPSettings *settings;OSQPCscMatrix* P = malloc(sizeof(OSQPCscMatrix));OSQPCscMatrix* A = malloc(sizeof(OSQPCscMatrix));/* Populate matrices */csc_set_data(A, m, n, A_nnz, A_x, A_i, A_p);csc_set_data(P, n, n, P_nnz, P_x, P_i, P_p);/* Set default settings */settings = (OSQPSettings *)malloc(sizeof(OSQPSettings));if (settings) osqp_set_default_settings(settings);/* Setup solver */exitflag = osqp_setup(&solver, P, q, A, l, u, m, n, settings);/* Solve problem */if (!exitflag) exitflag = osqp_solve(solver);/* Update problem */if (!exitflag) exitflag = osqp_update_data_vec(solver, q_new, l_new, u_new);/* Solve updated problem */if (!exitflag) exitflag = osqp_solve(work);/* Cleanup */osqp_cleanup(solver);if (A) free(A);if (P) free(P);if (settings) free(settings);return (int)exitflag;
};
③ Update matrices:更新矩阵P和A

#include <stdlib.h>
#include "osqp.h"int main(int argc, char **argv) {/* Load problem data */OSQPFloat P_x[3] = {4.0, 1.0, 2.0, };OSQPFloat P_x_new[3] = {5.0, 1.5, 1.0, };OSQPInt P_nnz = 3;OSQPInt P_i[3] = {0, 0, 1, };OSQPInt P_p[3] = {0, 1, 3, };OSQPFloat q[2] = {1.0, 1.0, };OSQPFloat q_new[2] = {2.0, 3.0, };OSQPFloat A_x[4] = {1.0, 1.0, 1.0, 1.0, };OSQPFloat A_x_new[4] = {1.2, 1.5, 1.1, 0.8, };OSQPInt A_nnz = 4;OSQPInt A_i[4] = {0, 1, 0, 2, };OSQPInt A_p[3] = {0, 2, 4, };OSQPFloat l[3] = {1.0, 0.0, 0.0, };OSQPFloat l_new[3] = {2.0, -1.0, -1.0, };OSQPFloat u[3] = {1.0, 0.7, 0.7, };OSQPFloat u_new[3] = {2.0, 2.5, 2.5, };OSQPInt n = 2;OSQPInt m = 3;/* Exitflag */OSQPInt exitflag = 0;/* Solver, settings, matrices */OSQPSolver *solver;OSQPSettings *settings;OSQPCscMatrix* P = malloc(sizeof(OSQPCscMatrix));OSQPCscMatrix* A = malloc(sizeof(OSQPCscMatrix));/* Populate matrices */csc_set_data(A, m, n, A_nnz, A_x, A_i, A_p);csc_set_data(P, n, n, P_nnz, P_x, P_i, P_p);/* Set default settings */settings = (OSQPSettings *)malloc(sizeof(OSQPSettings));if (settings) osqp_set_default_settings(settings);/* Setup solver */exitflag = osqp_setup(&solver, P, q, A, l, u, m, n, settings);/* Solve problem */if (!exitflag) exitflag = osqp_solve(solver);/* Update problemNB: Update only upper triangular part of P*/if (!exitflag) exitflag = osqp_update_data_mat(solver,P_x_new, OSQP_NULL, 3,A_x_new, OSQP_NULL, 4);/* Solve updated problem */if (!exitflag) exitflag = osqp_solve(work);/* Cleanup */osqp_cleanup(solver);if (A) free(A);if (P) free(P);if (settings) free(settings);return (int)exitflag;
};
应用:
① Huber fitting
② Lasso
③ Least-squares:最小二乘法
④ Model predictive control (MPC)
我们考虑将线性时不变动力系统控制到某个参考状态的问题。 为了实现这一点,我们使用约束线性二次 MPC,它在每个时间步长求解以下有限视界最优控制问题 x r ∈ R n x x_r∈R^{n_x} xr∈Rnx

⑤ Portfolio optimization
⑥ Support vector machine (SVM):支持向量机
相关文章:

OSQP文档学习
OSQP官方文档 1 QSQP简介 OSQP求解形式为的凸二次规划: x ∈ R n x∈R^n x∈Rn:优化变量 P ∈ S n P∈S^n_ P∈Sn:半正定矩阵 特征 (1)高效:使用了一种自定义的基于ADMM的一阶方法,只需…...

ONLYOFFICE 8.0:引领数字化办公新纪元
目录 前言 软件安装 软件启动 软件新版本特性 个人评价 总结 前言 在当今快节奏的数字化世界中,高效的办公软件已成为企业竞争力的关键因素。ONLYOFFICE,作为全球领先的办公解决方案提供商,始终致力于通过技术创新来优化用户体验。如今…...

「Linux」基础命令
目录结构 Linux只有1个顶级目录,称为“根目录”路径之间的层级关系,使用/来表示,例如:/usr/local/hello.txt 开头的/表示根目录后面的/表示层级关系 命令入门 命令的通用格式:command [ -options ] [ parameter] c…...

三防平板丨平板终端丨加固平板丨户外勘测应用
随着科技的不断发展,现代勘测业也在不断升级。相较于传统的勘测设备,三防平板在户外勘测中有着广泛的应用。那么,三防平板在户外勘测中究竟有哪些优势呢? 首先,三防平板具备极强的防水、防尘、防摔能力。在野外勘测中&…...
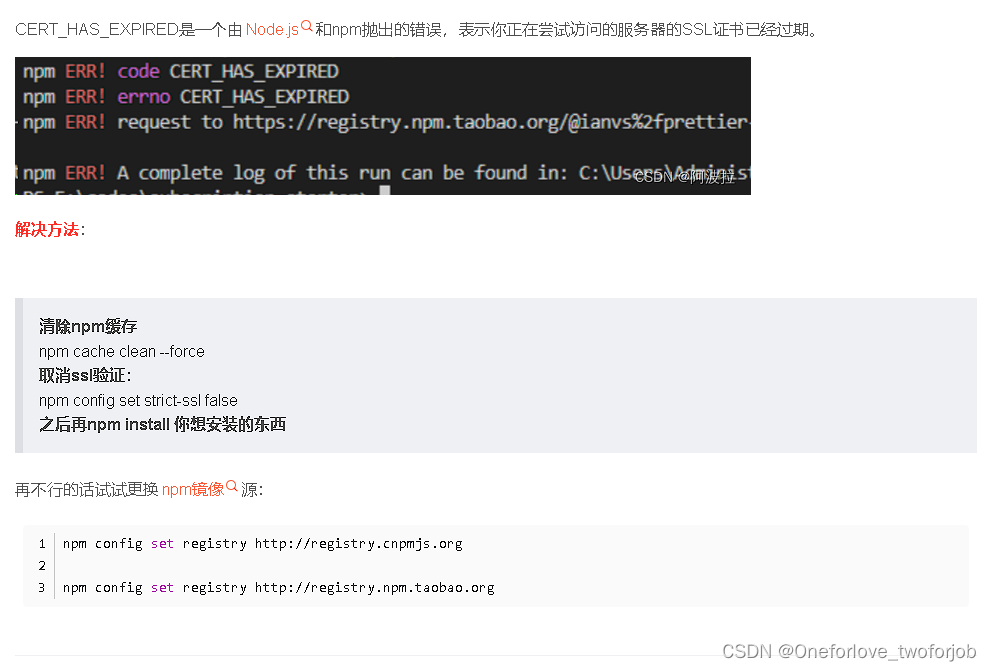
npm ERR! code CERT_HAS_EXPIRED:解决证书过期问题
转载:npm ERR! code CERT_HAS_EXPIRED:解决证书过期问题_npm err! code cert_has_expired npm err! errno cert-CSDN博客 npm config set registry http://registry.cnpmjs.org npm config set registry http://registry.npm.taobao.org...

npm报错之package-lock.json found. 问题和淘宝镜像源过期问题
1、package-lock.json found. 问题的解决 在执行yarn add react-transition-group -S 安装react-transition-group时出现package-lock.json found. Your project contains lock files generated by tools other than Yarn. It is advised not to mix package managers in orde…...

大模型提示学习、Prompting微调知识
为什么需要提示学习? 提示学习是一种在自然语言处理任务中引入人类编写的提示或示例来辅助模型生成更准确和有意义的输出的技术。以下是一些使用提示学习的原因: 解决模糊性:在某些任务中,输入可能存在歧义或模糊性,通…...
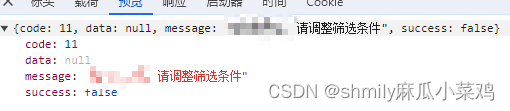
vue 导出,下载错误提示、blob与json数据转换
一、成功/失败 - 页面展示 失败 成功 二、成功/失败 - 接口请求/响应展示成功 2. 失败 三、解决 // 导出列表exportReceivedExcel() {if (this.tableCheckedValue) {this.form.ids this.tableCheckedValue.map(v > {return v.id || null})}this.loadingReceivedExcel …...

代码随想录算法训练营|二叉树总结
二叉树的定义: struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode():val(0),left(nullptr),right(nullptr){}TreeNode(int val):val(val),left(nullptr),right(nullptr){}TreeNode(int val,TreeNode* left,TreeNode* right):val(val),left(left),…...

rtt的io设备框架面向对象学习-uart设备
目录 1.uart设备基类2.uart设备基类的子类3.初始化/构造流程3.1设备驱动层3.2 设备驱动框架层3.3 设备io管理层 4.总结5.使用 1.uart设备基类 此层处于设备驱动框架层。也是抽象类。 在/ components / drivers / include / drivers 下的serial.h定义了如下uart设备基类 struc…...

PyCharm - Script parameters (脚本参数)
PyCharm - Script parameters [脚本参数] References Run -> Edit Configurations… -> Run/Debug Configurations -> Configuration -> Script parameters 命令行: python display_yolo_log.py ./person_training_log/person_train_log_DIMM40_stdout…...
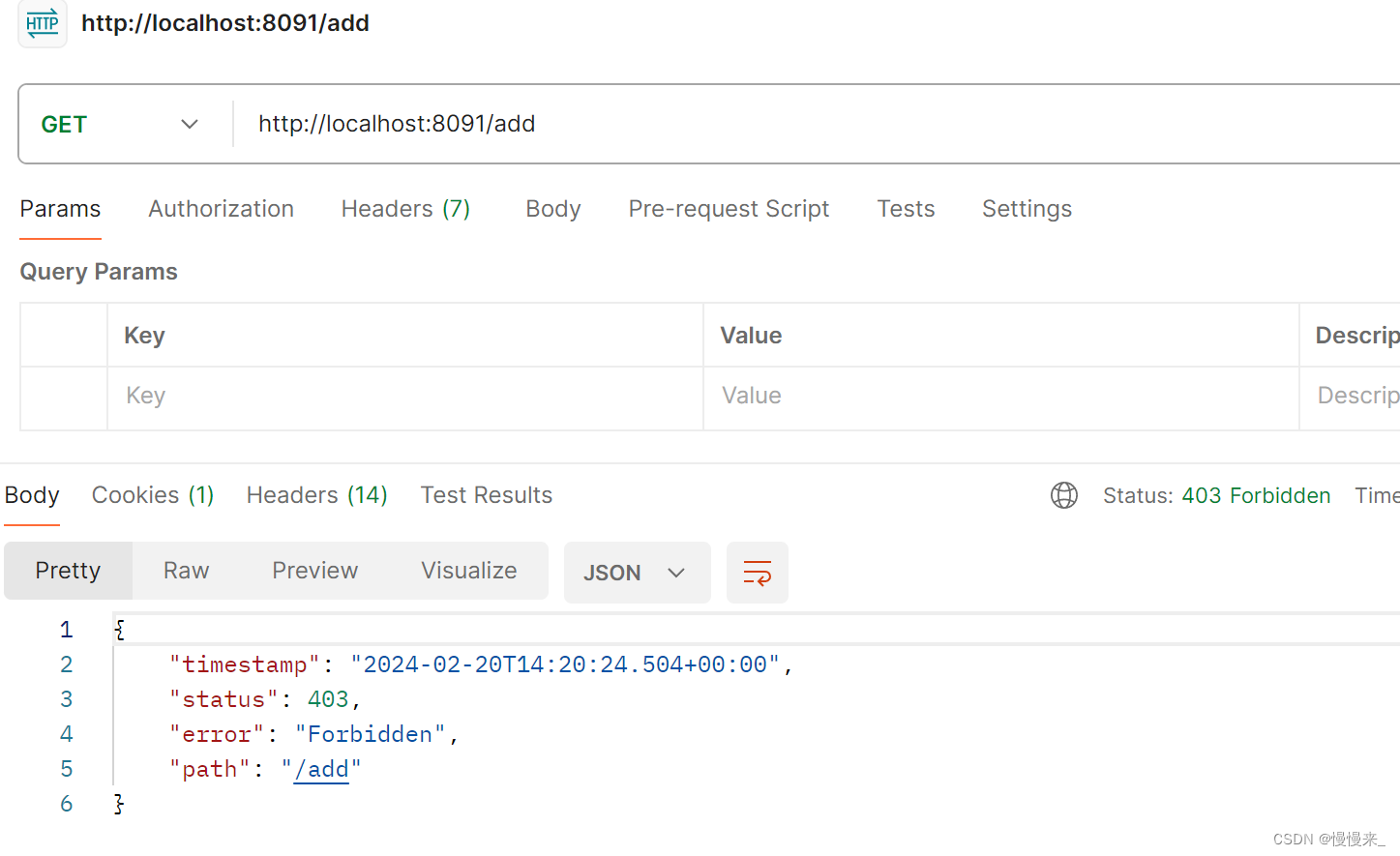
Security6.2 中的SpEL 表达式应用(权限注解使用)
最近学习若依框架,里面的权限注解涉及到了SpEL表达式 PreAuthorize("ss.hasPermi(system:user:list)"),若依项目中用的是自己写的方法进行权限处理, 也可以只用security 来实现权限逻辑代码,下面写如何用security 实现。…...
)
软考笔记--信息系统开发方法(下)
信息系统是一个极其复杂的人机交互系统,它不仅包含计算机技术,通信技术和网络规划以及其他的工程技术,而且,它还是一个复杂的管理系统,需要管理理论和方法的支持,因此,与其他工程项目相比&#…...
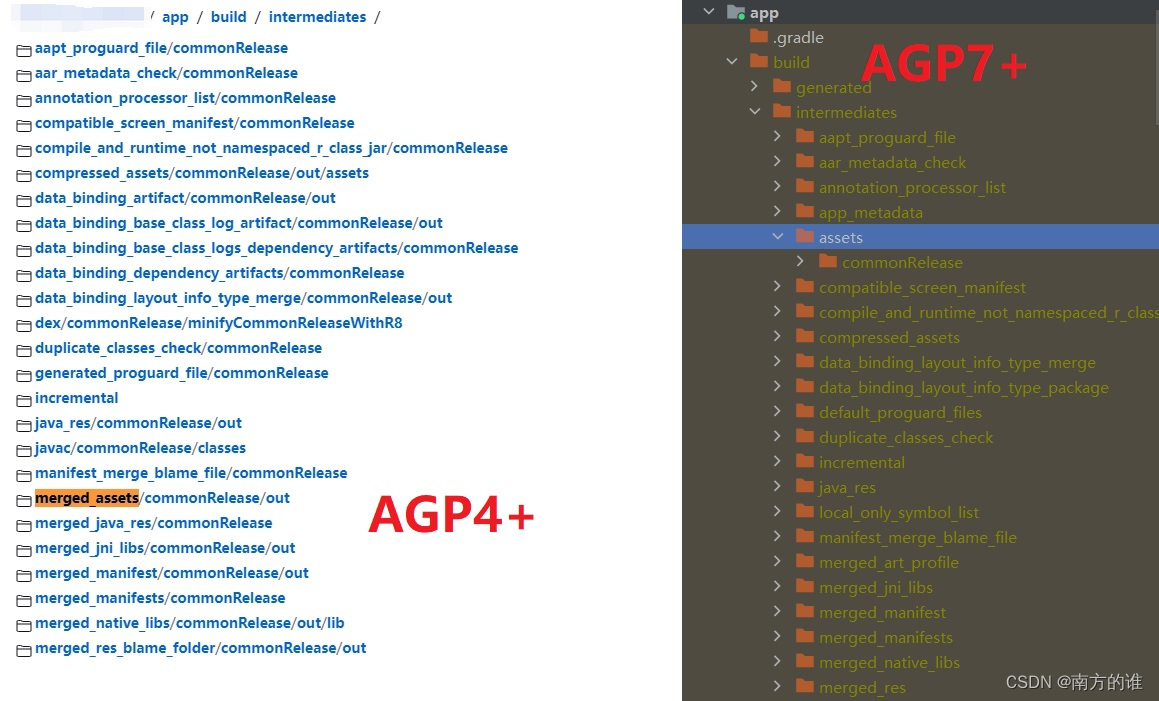
从 AGP 4.1.2 到 7.5.1——XmlParser、GPathResult、QName 过时
新年首发, 去年的问题,今年解决~ 问题 & 排查 1: Task failed with an exception. ----------- * What went wrong: Execution failed for task :app:processCommonReleaseManifest. > org.xml.sax.SAXParseException; lineNumber: 1; columnNu…...

spring boot 使用AOP实现是否已登录检测
前后端分离的开发中,用户http请求应用服务的接口时, 如果要求检测该用户是否已登录。可以实现的方法有多种, 本示例是通过aop 的方式实现,简单有效。 约定:前端http的post 请求 export async function request(url,data) {const …...

为什么从没有负值的数据中绘制的小提琴图(Violin Plot)会出现负值部分?
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 小提琴图(Violin Plot) 是一种用于展示和比较数据分布的可视化工具。它结合了箱形图(Box Plot)和密度图(Kernel Density Plot)的特…...

有哪几种行为会导致服务器被入侵
导致服务器被入侵的行为有很多种,以下是一些常见的行为: 系统漏洞:服务器操作系统或软件存在漏洞,攻击者可以通过利用这些漏洞获取系统权限,从而入侵服务器。 弱口令:服务器的账号密码过于简单或者未及时更…...

Redis RabbitMQ
Redis:轻量级,NoSQL数据库 redis是一个key-value存储系统。和Memcached类似,它支持存储的value类型相对更多,包括string(字符串)、list(链表)、set(集合)、zset(sorted set --有序集合)和hash(哈希类型)。这…...

http 和 https 的区别?
目录 1.http 和 https 的基本概念 2.http 和 https 的区别 3.https 协议的工作原理 4.https 协议的优点 5.https 协议的缺点 1.http 和 https 的基本概念 http: 超文本传输协议,是互联网上应用最为广泛的一种网络协议,是一个客户端和服务器端请求和…...

C++中线程的创建
线程创建 引言为什么要使用线程线程的创建使用函数指针示例运行结果使用类对象示例运行结果使用lambda表达式示例运行结果使用带参数的函数作为线程处理函数示例运行结果使用类成员函数示例运行结果引言 在学习C++的过程中,线程的使用作为一个非常重要的部分,也是在复杂项目…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
