代码随想录算法训练营|二叉树总结
二叉树的定义:
struct TreeNode
{int val;TreeNode* left;TreeNode* right;TreeNode():val(0),left(nullptr),right(nullptr){}TreeNode(int val):val(val),left(nullptr),right(nullptr){}TreeNode(int val,TreeNode* left,TreeNode* right):val(val),left(left),right(right){}
}
其实二叉树就是一种类似链表结构(故打好链表基础十分重要!)。
各种遍历方法

前序遍历
前序遍历的顺序是中左右,用一个图来感受这个过程,前序遍历:5412678
递归法
class Solution {
public:vector<int> result;void preorder(TreeNode* node){if(node==nullptr)return;result.push_back(node->val);preorder(node->left);preorder(node->right);}vector<int> preorderTraversal(TreeNode* root) {result.clear();preorder(root);return result;}
};
迭代法
上面我们采用递归能做出来,递归的本质就是栈,故迭代法可用栈这种数据结构!
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> stk;//先判断是否需要push进去,首先需要push一个root进去,不然下面的while循环都进不去if(root==nullptr) return result;stk.push(root);while(!stk.empty()){TreeNode* node=stk.top();stk.pop();result.push_back(node->val);//一个注意点,应该先push右子树,因为栈的特点是先入后出if(node->right)stk.push(node->right);if(node->left)stk.push(node->left);}return result;}
};
中序遍历
递归法
中序遍历的顺序为左中右,参考上面的图,应该是1425768
class Solution {
public:vector<int> result;void inorder(TreeNode* node){if(node==nullptr)return;preorder(node->left);result.push_back(node->val);preorder(node->right);}vector<int> inorderTraversal(TreeNode* root) {result.clear();inorder(root);return result;}
};
迭代法
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*>stk;if(root==nullptr)return result;TreeNode* cur=root;while(!stk.empty()||cur!=nullptr){if(cur){stk.push(cur);cur=cur->left;}else{cur=stk.top();stk.pop();result.push_back(cur->val);cur=cur->right;}}return result;}
};
后序遍历
后序遍历:左右中,参考上面的图:1247865
递归法
class Solution {
public:vector<int> result;void postorder(TreeNode* node){if(node==nullptr)return;preorder(node->left);preorder(node->right);result.push_back(node->val);}vector<int> postorderTraversal(TreeNode* root) {result.clear();postorder(root);return result;}
};
迭代法
对比前序遍历顺序:中左右,后序遍历顺序为:左右中,如果我们将顺序变为:中右左,然后对于结果反转一下,是不是就是正确的呢?
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> stk;if(root==nullptr)return result;stk.push(root);while(!stk.empty()){TreeNode* node=stk.top();stk.pop();result.push_back(node->val);if(node->left)stk.push(node->left);if(node->right)stk.push(node->right);}reverse(result.begin(),result.end());return result;}
};
层序遍历
其实上文的前中后序遍历,在图论中就是DFS(深度优先搜索),而对应还有一种方法,那就是宽度优先搜索(BFS),其实对于BFS而言,用处还是蛮大的,很多需要遍历整个树的问题,用BFS做起来蛮方便的!当然要想实现BFS,也要借用一种数据结构,其用于存储每一层的元素!这种数据结构就是queue
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>>result;queue<TreeNode*> que;if(root==nullptr)return result;que.push(root);while(!que.empty()){int size=que.size();vector<int>vec;//在遍历上一层的同时,也将下一层的节点加入queue,这个过程while(size--){TreeNode* node=que.front();que.pop();vec.push_back(node->val);if(node->left)que.push(node->left);if(node->right)que.push(node->right);}result.push_back(vec);}return result;}
};
二叉树遍历(带有回溯的)
236.二叉树的最近公共祖先
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==nullptr||root==p||root==q)return root;TreeNode* left=lowestCommonAncestor(root->left,p,q);TreeNode* right=lowestCommonAncestor(root->right,p,q);if(left&&right)return root;else if(left==nullptr&&right)return right;else if(left&&right==nullptr)return left;else return nullptr;}
};
做完这道题,明白了公共祖先的问题,都是自顶向上的遍历(采用后序遍历)以及搜索整个树采用:
TreeNode* left=lowestCommonAncestor(root->left,p,q);TreeNode* right=lowestCommonAncestor(root->right,p,q);
同样的一道题:255.二叉搜索树的最近公共祖先,但是这道题还有一个特点,每次要遍历左子树还是右子树的时候可以先进行判断,相当于进行剪枝操作了!
分解问题
将一个二叉树分解为左子树和右子树的问题!
其实要求遍历整个树的问题,很多时候都是分解问题,比较左子树和右子树的问题!
222.完全二叉树的节点个数
这是一道最基本的分解问题,求整个树的个数,分解为左子树加右子树再加根节点!(当然这里还有要遍历整个树要怎么写的问题!)
class Solution {
public:int traversal(TreeNode* node){if(node==nullptr)return 0;int left=traversal(node->left);int right=traversal(node->right);//为什么这里是1+left+right呢?相当于左子树的个数加上右子树的个数再加上根节点(分解问题)return 1+left+right;}int countNodes(TreeNode* root) {return traversal(root);}
};
构造二叉树
关键点:在于不断确定中间节点,左子树以及右子树!
105.从前序与中序遍历序列构造二叉树
class Solution {
public:TreeNode* traversal(vector<int>& preorder,vector<int>& inorder){if(preorder.size()==0)return nullptr;int rootvalue=preorder[0];TreeNode* root=new TreeNode(rootvalue);int index=0;for(;index<inorder.size();index++){if(inorder[index]==rootvalue)break;}vector<int> leftinorder(inorder.begin(),inorder.begin()+index);vector<int> rightinorder(inorder.begin()+index+1,inorder.end());vector<int> leftpreorder(preorder.begin()+1,preorder.begin()+1+leftinorder.size());vector<int> rightpreorder(preorder.begin()+1+leftinorder.size(),preorder.end());root->left=traversal(leftpreorder,leftinorder);root->right=traversal(rightpreorder,rightinorder);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.size()==0||inorder.size()==0) return nullptr;return traversal(preorder,inorder);}
};
做过这道题,可以试试看
106.从中序与后序遍历序列构造二叉树
二叉搜索树
1.有序的问题!(联系中序遍历),求二叉搜索树中第k个最小值!一般做法:采用中序遍历,将二叉树变为有序数组,一定要采用中序遍历!
230.二叉搜索树中第K小的元素
class Solution {
public:vector<int> result;void inorder(TreeNode* root){if(root==nullptr)return;inorder(root->left);result.push_back(root->val);inorder(root->right);}int kthSmallest(TreeNode* root, int k) {inorder(root);return result[k-1];}
};
98.验证二叉搜索树
这两道题都是将二叉搜索树的问题转换成数组问题来解决的!故对于二叉搜索树的很多问题一定要学会联系中序遍历!
路径问题
插入节点
701.二叉搜索树中的插入操作
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if(root==nullptr){TreeNode* node=new TreeNode(val);return node;}if(root->val<val){root->right=insertIntoBST(root->right,val);}if(root->val>val){root->left=insertIntoBST(root->left,val);}return root;}
};
删除节点
450.删除二叉搜索树的节点
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if(root==nullptr)return nullptr;if(root->val==key){if(root->left==nullptr)return root->right;else if(root->right==nullptr)return root->left;else if(root->left!=nullptr && root->right!=nullptr){TreeNode* cur=root->right;while(cur->left!=nullptr){cur=cur->left;}cur->left=root->left;TreeNode* temp=root;root=root->right;delete temp;return root;}}if(root->val<key)root->right=deleteNode(root->right,key);if(root->val>key)root->left=deleteNode(root->left,key);return root;}
};
相关文章:

代码随想录算法训练营|二叉树总结
二叉树的定义: struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode():val(0),left(nullptr),right(nullptr){}TreeNode(int val):val(val),left(nullptr),right(nullptr){}TreeNode(int val,TreeNode* left,TreeNode* right):val(val),left(left),…...

rtt的io设备框架面向对象学习-uart设备
目录 1.uart设备基类2.uart设备基类的子类3.初始化/构造流程3.1设备驱动层3.2 设备驱动框架层3.3 设备io管理层 4.总结5.使用 1.uart设备基类 此层处于设备驱动框架层。也是抽象类。 在/ components / drivers / include / drivers 下的serial.h定义了如下uart设备基类 struc…...

PyCharm - Script parameters (脚本参数)
PyCharm - Script parameters [脚本参数] References Run -> Edit Configurations… -> Run/Debug Configurations -> Configuration -> Script parameters 命令行: python display_yolo_log.py ./person_training_log/person_train_log_DIMM40_stdout…...
Security6.2 中的SpEL 表达式应用(权限注解使用)
最近学习若依框架,里面的权限注解涉及到了SpEL表达式 PreAuthorize("ss.hasPermi(system:user:list)"),若依项目中用的是自己写的方法进行权限处理, 也可以只用security 来实现权限逻辑代码,下面写如何用security 实现。…...
)
软考笔记--信息系统开发方法(下)
信息系统是一个极其复杂的人机交互系统,它不仅包含计算机技术,通信技术和网络规划以及其他的工程技术,而且,它还是一个复杂的管理系统,需要管理理论和方法的支持,因此,与其他工程项目相比&#…...
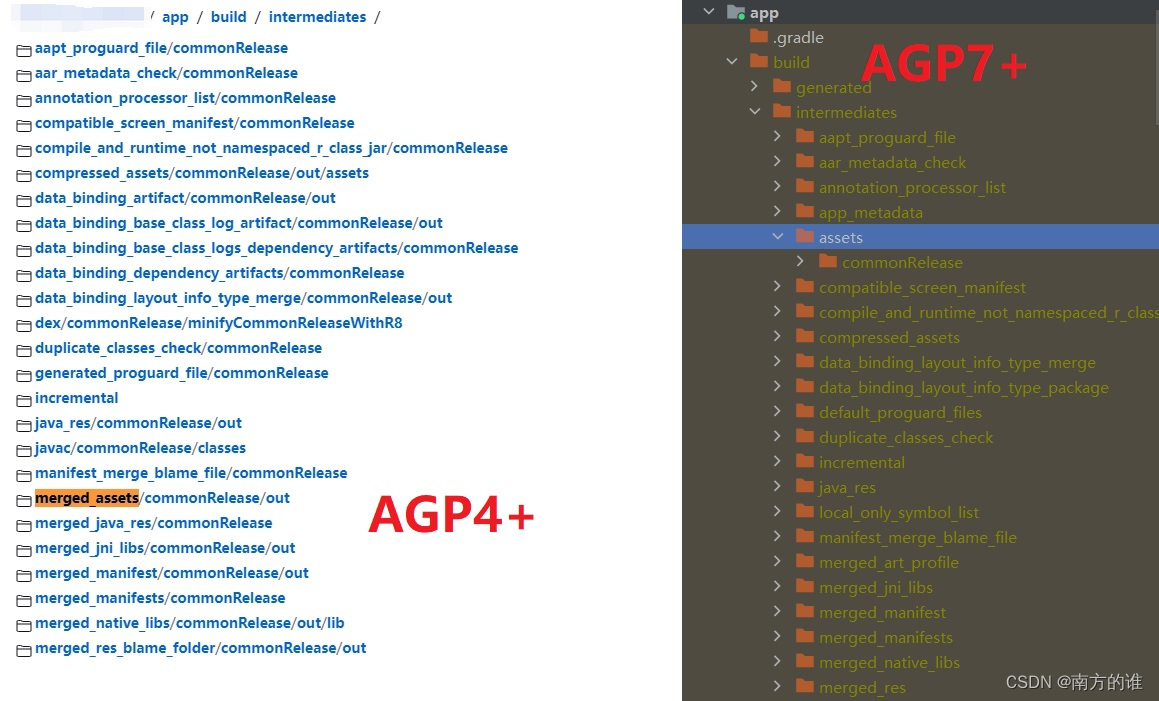
从 AGP 4.1.2 到 7.5.1——XmlParser、GPathResult、QName 过时
新年首发, 去年的问题,今年解决~ 问题 & 排查 1: Task failed with an exception. ----------- * What went wrong: Execution failed for task :app:processCommonReleaseManifest. > org.xml.sax.SAXParseException; lineNumber: 1; columnNu…...

spring boot 使用AOP实现是否已登录检测
前后端分离的开发中,用户http请求应用服务的接口时, 如果要求检测该用户是否已登录。可以实现的方法有多种, 本示例是通过aop 的方式实现,简单有效。 约定:前端http的post 请求 export async function request(url,data) {const …...

为什么从没有负值的数据中绘制的小提琴图(Violin Plot)会出现负值部分?
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 小提琴图(Violin Plot) 是一种用于展示和比较数据分布的可视化工具。它结合了箱形图(Box Plot)和密度图(Kernel Density Plot)的特…...

有哪几种行为会导致服务器被入侵
导致服务器被入侵的行为有很多种,以下是一些常见的行为: 系统漏洞:服务器操作系统或软件存在漏洞,攻击者可以通过利用这些漏洞获取系统权限,从而入侵服务器。 弱口令:服务器的账号密码过于简单或者未及时更…...

Redis RabbitMQ
Redis:轻量级,NoSQL数据库 redis是一个key-value存储系统。和Memcached类似,它支持存储的value类型相对更多,包括string(字符串)、list(链表)、set(集合)、zset(sorted set --有序集合)和hash(哈希类型)。这…...

http 和 https 的区别?
目录 1.http 和 https 的基本概念 2.http 和 https 的区别 3.https 协议的工作原理 4.https 协议的优点 5.https 协议的缺点 1.http 和 https 的基本概念 http: 超文本传输协议,是互联网上应用最为广泛的一种网络协议,是一个客户端和服务器端请求和…...

C++中线程的创建
线程创建 引言为什么要使用线程线程的创建使用函数指针示例运行结果使用类对象示例运行结果使用lambda表达式示例运行结果使用带参数的函数作为线程处理函数示例运行结果使用类成员函数示例运行结果引言 在学习C++的过程中,线程的使用作为一个非常重要的部分,也是在复杂项目…...
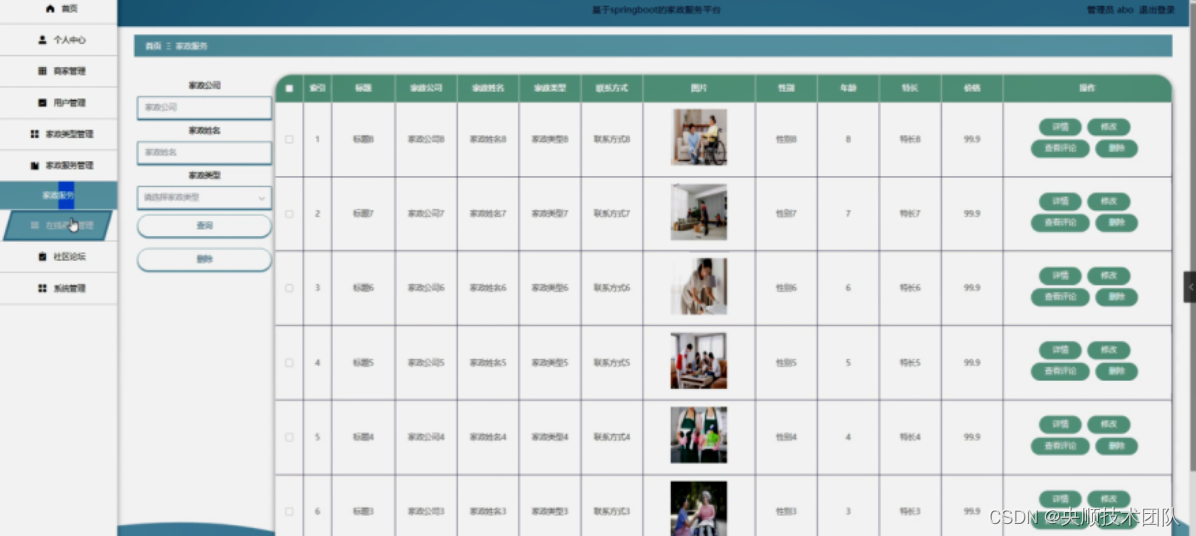
基于JavaWeb开发的家政服务平台计算机毕业设计[附源码]
基于JavaWeb开发的家政服务平台计算机毕业设计[附源码] 🍅 作者主页 央顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 🍅 查看下方微信号获取联系方式 承接各种定制系统…...

性能调优:容易忽视的JavaScript标签属性及其性能影响
在性能优化中,我们都知道,async属性可以让script标签变得不阻塞HTML解析,defer属性也有类似的功能,但实际defer是会阻塞script解析的(用defer的话,多个script会按顺序执行,而async执行是无序的&…...

【机器学习笔记】7 KNN算法
距离度量 欧氏距离(Euclidean distance) 欧几里得度量(Euclidean Metric)(也称欧氏距离)是一个通常采用的距离定义,指在𝑚维空间中两个点之间的真实距离,或者向量的自然长度(即该点…...

mysql 2-20
TEXT类型 枚举类型 SET类型 二进制字符串类型 BLOB类型 注意事项 JSON类型 提取数据 空间类型 选择建议 约束...

Unity3D Shader 素描风格渲染管线实现详解
前言 在游戏开发中,渲染效果是非常重要的一部分,它可以直接影响游戏的视觉效果和玩家的体验。而素描风格的渲染效果是一种非常独特和有趣的风格,可以为游戏增添一种艺术氛围。在Unity3D中,可以通过编写Shader来实现素描风格的渲染…...

WordPress站点如何实现发布文章即主动推送到百度快速收录和普通收录?
我们在WordPress后台成功发布文章之后,如果靠搜索引擎来抓取的话,可能会比较慢,所以十分有必要将我们成功发布的文章马上提交到百度、必应等搜索引擎中。下面boke112百科就跟大家说一说WordPress站点如何实现发布文章即主动推送到百度快速收录…...
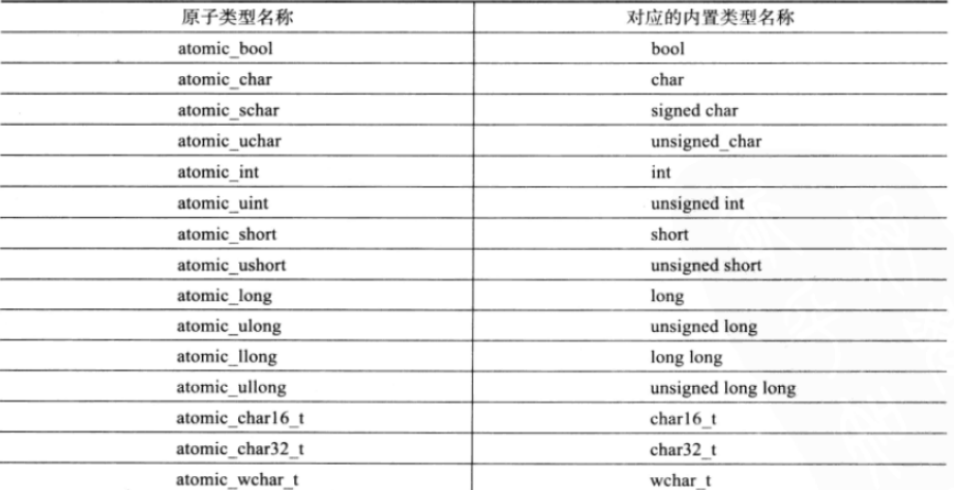
C++11---(3)
目录 一、可变参数模板 1.1、可变参数模板的概念 1.2、可变参数模板的定义方式 1.3、如何获取可变参数 二、lambda表达式 2.1、Lamabda表达式定义 2.2、为什么有Lambda 2.3、Lambda表达式的用法 2.4、函数对象与lambda表达式 三、包装器 3.1、function 3.2、bind …...
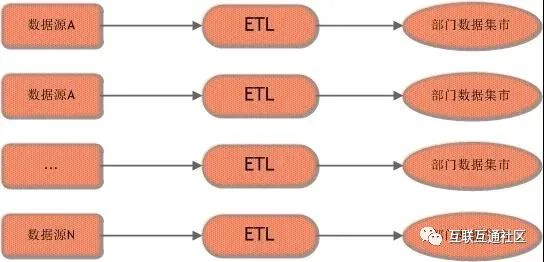
【常识】大数据设计基础知识
底层存储:hadoop(hdfsmapreduce) Hadoop已经有十几年的历史,它是大数据领域的存储基石,HDFS目前仍然没有成熟替代品;MapR 文件系统在业内已经具有一定知名度了,不仅 MapR 宣布它自己的文件系统比 HDFS 快2-…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
