【机器学习笔记】7 KNN算法
距离度量
欧氏距离(Euclidean distance)

欧几里得度量(Euclidean Metric)(也称欧氏距离)是一个通常采用的距离定义,指在𝑚维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离)。在二维和三维空间中的欧氏距离就是两点之间的实际距离。

曼哈顿距离(Manhattan distance)

想象你在城市道路里,要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直
线距离吗?显然不是,除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源, 曼哈顿距离也称为城市街区距离(City Block distance)

切比雪夫距离(Chebyshev distance)

二个点之间的距离定义是其各坐标数值差绝对值的最大值。国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数。由于王可以往斜前或斜后方向移动一格,因此可以较有效率的到达目的的格子。上图是棋盘上所有位置距f6位置的切比雪夫距离。

闵可夫斯基距离(Minkowski distance)

𝑝取1或2时的闵氏距离是最为常用的
𝑝 = 2即为欧氏距离,
𝑝 = 1时则为曼哈顿距离。
当𝑝取无穷时的极限情况下,可以得到切比雪夫距离
汉明距离(Hamming distance)

汉明距离是使用在数据传输差错控制编码里面的,汉明距离是一个概念,它表示两个(相同长度)字对应位不同的数量,我们以表示两个字之间的汉明距离。对两个字符串进行异或运算,并统计结果为1的个数,那么这个数就是汉明距离。

余弦相似度
两个向量有相同的指向时,余弦相似度的值为1;两个向量夹角为90°时,余弦相似度的值为0;两个向量指向完全相反的方向时,余弦相似度的值为-1。

假定𝐴和𝐵是两个𝑛维向量,𝐴是 𝐴1, 𝐴2, … , 𝐴𝑛 ,𝐵是𝐵1,𝐵2, … , 𝐵𝑛 ,则𝐴和𝐵的夹角的余弦等于:


KNN算法
𝑘近邻法(k-Nearest Neighbor,kNN)是一种比较成熟也是最简单的机器学习算法,可以用于基本的分类与回归方法。
算法的主要思路
如果一个样本在特征空间中与𝑘个实例最为相似(即特征空间中最邻近),那么这𝑘个实例中大多数属于哪个类别,则该样本也属于这个类别。
对于分类问题:
对新的样本,根据其𝑘个最近邻的训练样本的类别,通过多数表决等方式进行预测。
对于回归问题:
对新的样本,根据其𝑘个最近邻的训练样本标签值的均值作为预测值
𝑘近邻法的三要素
• 𝑘值选择。
• 距离度量。
• 决策规则。
算法流程
1.计算测试对象到训练集中每个对象的距离
2.按照距离的远近排序
3.选取与当前测试对象最近的k的训练对象,作为该测试对象的邻居
4.统计这k个邻居的类别频次
5.k个邻居里频次最高的类别,即为测试对象的类
 以上图中绿点位置的分类问题为例,图中有正方形和三角形两类,K=3即选取距离绿点最近的三个对象,这三个对象中三角形的类别较多因此将绿点位置归为三角形类,而当K=5时选取距离绿点位置最近的五个对象,此时正方形的数量较多,则此时绿点为正方形类
以上图中绿点位置的分类问题为例,图中有正方形和三角形两类,K=3即选取距离绿点最近的三个对象,这三个对象中三角形的类别较多因此将绿点位置归为三角形类,而当K=5时选取距离绿点位置最近的五个对象,此时正方形的数量较多,则此时绿点为正方形类
KD树划分
KD树(K-Dimension Tree),,也可称之为K维树,可以用更高的效率来对空间进行划分,并且其结构非常适合寻找最近邻居和碰撞检测。
假设有 6 个二维数据点,构建KD树的过程:𝐷 = (2,3), (5,7), (9,6), (4,5), (6,4), (7,2) 。
①从𝑥轴开始划分,根据𝑥轴的取值2,5,9,4,6,7得到中位数为6 ,因此切分线为:𝑥 = 6 。

②可以根据𝑥轴和𝑦轴上数据的方差,选择方差最大的那个轴作为第一轮划分轴。
左子空间(记做 𝐷1)包含点 (2,3),(4,5),(5,7),切分轴轮转,从𝑦轴开始划分,切分线为𝑦 = 5
右子空间(记做 𝐷2 )包含点 (9,6),(7,2),切分轴轮转,从𝑦轴开始划分,切分线为:𝑦 = 6 。

③𝐷1的左子空间(记做 𝐷3)包含点(2,3),切分轴轮转,从x 轴开始划分,切分线为:𝑥 = 2。
其左子空间记做 𝐷7 ,右子空间记做 𝐷8 。由于 𝐷7,𝐷8都不包含任何点,因此对它们不再继续拆分。
𝐷1 的右子空间(记做 𝐷4 )包含点(5,7),切分轴轮转,从x 轴开始划分,切分线为:𝑥 = 5。
其左子空间记做 𝐷9,右子空间记做 𝐷10 。由于𝐷9,𝐷10都不包含任何点,因此对它们不再继续拆分。

④𝐷2的左子空间(记做 𝐷5 )包含点(7,2),切分轴轮转,从x 轴开始划分,切分线为:𝑥 = 7。
其左子空间记做 𝐷11,右子空间记做 𝐷12 。由于𝐷11,𝐷12 都不包含任何点,因此对它们不再继续拆分。
𝐷2的右子空间(记做 𝐷6)不包含任何点,停止继续拆分。



KD树搜索
1.首先要找到该目标点的叶子节点,然后以目标点为圆心,目标点到叶子节点的距离为半径,建立一个超球体,我们要找寻的最近邻点一定是在该球体内部。
搜索(4,4)的最近邻时。首先从根节点(6,4)出发,将当前最近邻设为(6,4),对该KD树作深度优先遍历。以(4,4)为圆心,其到(6,4)的距离为半径画圆(多维空间为超球面),可以看出(7,2)右侧的区域与该圆不相交,所以(7,2)的右子树全部忽略。

2.返回叶子结点的父节点,检查另一个子结点包含的超矩形体是否和超球体相交,如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。
接着走到(6,4)左子树根节点(4,5),与原最近邻对比距离后,更新当前最近邻为(4,5)。以(4,4)为圆心,其到(4,5)的距离为半径画圆,发现(6,4)右侧的区域与该圆不相交,忽略该侧所有节点,这样(6,4)的整个右子树被标记为已忽略

3.如果不相交直接返回父节点,在另一个子树继续搜索最近邻。
4.当回溯到根节点时,算法结束,此时保存的最近邻节点就是最终的最近邻。遍历完(4,5)的左右叶子节点,发现与当前最优距离相等,不更新最近邻。所以(4,4)的最近邻为(4,5)。
相关文章:

【机器学习笔记】7 KNN算法
距离度量 欧氏距离(Euclidean distance) 欧几里得度量(Euclidean Metric)(也称欧氏距离)是一个通常采用的距离定义,指在𝑚维空间中两个点之间的真实距离,或者向量的自然长度(即该点…...

mysql 2-20
TEXT类型 枚举类型 SET类型 二进制字符串类型 BLOB类型 注意事项 JSON类型 提取数据 空间类型 选择建议 约束...

Unity3D Shader 素描风格渲染管线实现详解
前言 在游戏开发中,渲染效果是非常重要的一部分,它可以直接影响游戏的视觉效果和玩家的体验。而素描风格的渲染效果是一种非常独特和有趣的风格,可以为游戏增添一种艺术氛围。在Unity3D中,可以通过编写Shader来实现素描风格的渲染…...

WordPress站点如何实现发布文章即主动推送到百度快速收录和普通收录?
我们在WordPress后台成功发布文章之后,如果靠搜索引擎来抓取的话,可能会比较慢,所以十分有必要将我们成功发布的文章马上提交到百度、必应等搜索引擎中。下面boke112百科就跟大家说一说WordPress站点如何实现发布文章即主动推送到百度快速收录…...
C++11---(3)
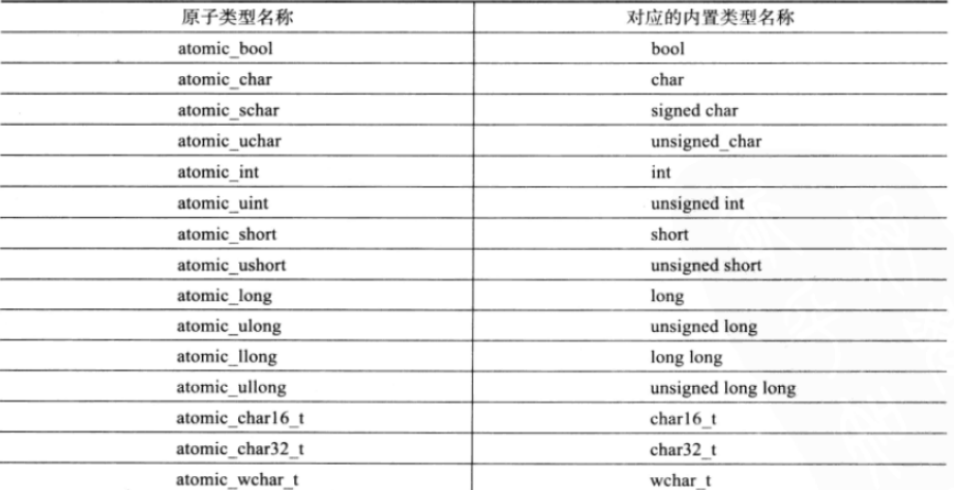
目录 一、可变参数模板 1.1、可变参数模板的概念 1.2、可变参数模板的定义方式 1.3、如何获取可变参数 二、lambda表达式 2.1、Lamabda表达式定义 2.2、为什么有Lambda 2.3、Lambda表达式的用法 2.4、函数对象与lambda表达式 三、包装器 3.1、function 3.2、bind …...
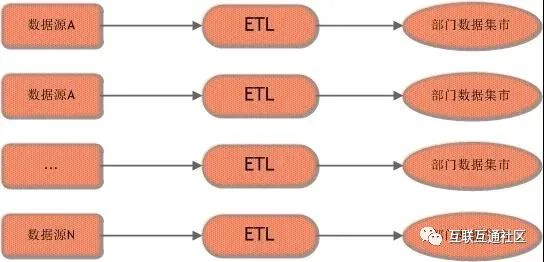
【常识】大数据设计基础知识
底层存储:hadoop(hdfsmapreduce) Hadoop已经有十几年的历史,它是大数据领域的存储基石,HDFS目前仍然没有成熟替代品;MapR 文件系统在业内已经具有一定知名度了,不仅 MapR 宣布它自己的文件系统比 HDFS 快2-…...
)
Vue:Vuex模块化编码(非常实用)
一、情景说明 通过前面的学习,我们知道,Vuex的核心文件就是indexc.js 这个文件里面,主要是四个对象 actions、mutations、state、getters 那么,随着业务的复杂化,所有的逻辑都写在一个actions里面吗? 显然…...

springboot 异步执行方法详细介绍
在Spring Boot中,异步执行方法是一种提高应用程序性能和响应性的技术。通过异步执行,你可以在处理耗时的业务逻辑时,不需要阻塞当前线程,从而提高应用程序的吞吐量和并发处理能力。 基本概念 在Spring中ÿ…...

拿捏c语言指针(下)
前言 此篇讲解的主要是函数与指针的那些事~ 书接上回 拿捏c语言指针(上)和 拿捏c语言指针(中) 没有看的小伙伴要抓紧喽~ 欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误&#x…...
什么是BeanFactory?)
Spring源码笔记之SpringIOC--(3)什么是BeanFactory?
什么是BeanFactory? BeanFactory是SpringIOC的最顶层接口,涵盖了IOC容器最基本的操作。ListableBeanFactory、ConfigurableBeanFactory提供了IOC容器获取所有Bean、配置Bean的额外能力。所有BeanFactory的实现类持有所有Bean的定义BeanDefinition&#…...

微信小程序之会议OA个人中心后台交互
目录 获取用户昵称头像和昵称 小程序登录 登录-小程序 wx.checkSession wx.login wx.request 后台 准备数据表 反向生成工具生成 准备封装前端传过来的数据 小程序服器配置 导入微信小程序SDK application.yml WxProperties WxConfig WxAuthController 登录-小…...

代码随想录算法训练营第52天(动态规划09 ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
动态规划part09 198.打家劫舍解题思路 213.打家劫舍II解题思路 337.打家劫舍III解题思路 今天就是打家劫舍的一天,这个系列不算难,大家可以一口气拿下。 198.打家劫舍 题目链接: 198.打家劫舍 视频讲解: 198.打家劫舍 文章讲解&…...
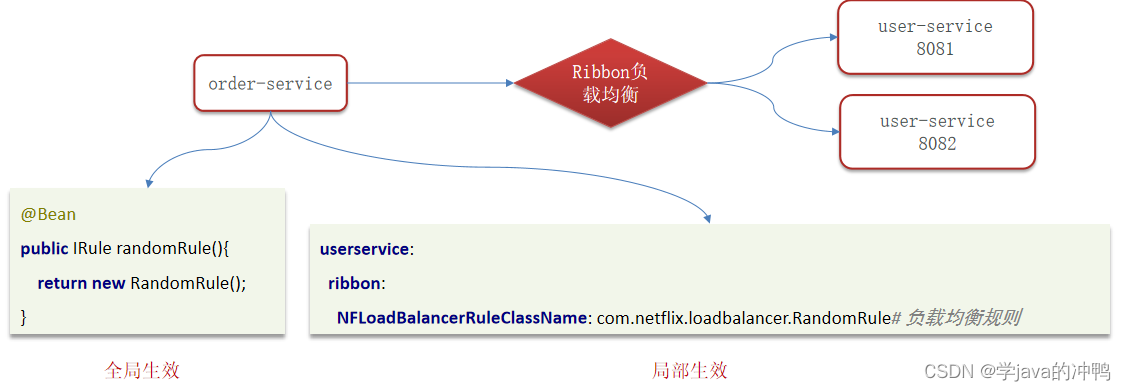
微服务篇之负载均衡
一、Ribbon负载均衡流程 二、Ribbon负载均衡策略 1. RoundRobinRule:简单轮询服务列表来选择服务器。 2. WeightedResponseTimeRule:按照权重来选择服务器,响应时间越长,权重越小。 3. RandomRule:随机选择一个可用的服…...
 + egl + opengles 使用FBO渲染到纹理实例(六))
wayland(xdg_wm_base) + egl + opengles 使用FBO渲染到纹理实例(六)
文章目录 前言一、FBO介绍1. FBO 简介2. FBO的关键组成部分3. FBO的基本工作流程4. FBO 实现渲染到纹理5. FBO 实现离屏渲染二、FBO 实现渲染到纹理的代码实例1. egl_wayland_texture3_2.c2. xdg-shell-client-protocol.h 和 xdg-shell-protocol.c3. 编译4. 运行总结参考资料前…...

基于 RisingWave、Instaclustr 和 Apache Superset 对维基百科实时监控
得益于 RisingWave 和 Kafka 等流处理工具, 数据工程师能实时洞察流数据中的重要信息。这能够助力制定决策,并在多个层面改善用户体验,包括推荐系统、金融、物流、汽车、制造业、 IIOT 设备和零售。 在这篇博客中,我们会把 Risin…...

建站用帝国CMS好还是WordPress好
随着互联网的迅猛发展,内容管理系统(CMS)在网站建设中扮演着越来越重要的角色。在众多CMS中,帝国CMS和WordPress因其强大的功能和广泛的用户基础而备受关注。本文将对这两种CMS进行详细比较,分析它们的优势与不足,以便用户能够根据…...
—图》)
深度学习基础之《TensorFlow框架(2)—图》
一、什么是图结构 1、图包含了一组tf.Operation代表的计算单元对象和tf.Tensor代表的计算单元之间流动的数据 图结构:数据(Tensor) 操作(Operation) 二、图相关操作 1、默认图 通常TensorFlow会默认帮我们创建一张图 查看默认图的两种方法: &#x…...

Web3区块链游戏:创造虚拟世界的全新体验
随着区块链技术的不断发展,Web3区块链游戏正逐渐崭露头角,为玩家带来了全新的虚拟世界体验。传统游戏中的中心化结构和封闭经济体系已经被打破,取而代之的是去中心化的游戏环境和真实所有权的数字资产。本文将深入探讨Web3区块链游戏的特点、…...

单机启动/开机启动SpringBoot服务的正确方式
此操作只针对于测试环境或单机部署的情况下,使用Jenkins自动化部署或docker部署SpringBoot服务请忽略。 SpringBoot单机启动和集群启动的区别: 部署方式:单机启动可以直接运行jar文件或使用IDE启动应用程序,而双机集群启动需要将…...

[C#]winform基于opencvsharp结合CSRNet算法实现低光图像增强黑暗图片变亮变清晰
【算法介绍】 "Conditional Sequential Modulation for Efficient Global Image Retouching" 是一种图像修饰方法,主要用于对图像进行全局的高效调整。该方法基于深度学习技术,通过引入条件向量来实现对图像特征的调制,以达到改善…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
