代码随想录算法训练营第52天(动态规划09 ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
动态规划part09
- 198.打家劫舍
- 解题思路
- 213.打家劫舍II
- 解题思路
- 337.打家劫舍III
- 解题思路
今天就是打家劫舍的一天,这个系列不算难,大家可以一口气拿下。
198.打家劫舍
题目链接: 198.打家劫舍
视频讲解: 198.打家劫舍
文章讲解: 198.打家劫舍
解题思路
递归五部曲
- 确定dp数组以及下标的含义
dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。 - 确定递推公式
dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出 下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。 - dp数组如何初始化
递推公式的基础就是dp[0] 和 dp[1]
dp[0] = nums[0],dp[1] = max(nums[0], nums[1]); - 遍历顺序
从前到后 - 举例推导dp数组
// 动态规划
class Solution {public int rob(int[] nums) {if(nums == null || nums.length == 0) return 0;if(nums.length == 1) return nums[0];int[] dp = new int[nums.length];dp[0] = nums[0];dp[1] = Math.max(dp[0], nums[1]);for(int i = 2; i < nums.length; i++){dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);}return dp[nums.length - 1];}
}
213.打家劫舍II
题目链接: 213.打家劫舍II
视频讲解: 213.打家劫舍II
文章讲解: 213.打家劫舍II
解题思路
对于一个数组,成环的话主要有如下三种情况:
情况一:考虑不包含首尾元素
情况二:考虑包含首元素,不包含尾元素
情况三:考虑包含尾元素,不包含首元素
而情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了。
分析到这里,剩下的和198.打家劫舍就是一样的了。
class Solution {public int rob(int[] nums) {if(nums == null || nums.length == 0) return 0;if(nums.length == 1) return nums[0];return Math.max(robAction(nums, 0, nums.length - 1), robAction(nums, 1, nums.length));}int robAction(int[] nums, int start, int end) {int dp3 = 0;int dp2 = 0;int dp1 = 0;for(int i = start; i < end; i++){dp1 = dp3;dp3 = Math.max(dp1, dp2 + nums[i]);dp2 = dp1;}return dp3;}// 运行没通过 不知道为啥// int robAction(int[] nums, int start, int end) {// int[] dp = new int[nums.length];// dp[start] = nums[start];// dp[start + 1] = Math.max(dp[0], nums[start + 1]);// for(int i = start + 2; i < end; i++){// dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);// }// return dp[end - 1];// }
}
337.打家劫舍III
题目链接: 337.打家劫舍III
视频讲解: 337.打家劫舍III
文章讲解: 337.打家劫舍III
解题思路
动态规划和二叉树的结合
动态规划其实就是使用状态转移容器来记录状态的变化,这里可以使用一个长度为2的数组,记录当前节点偷与不偷所得到的的最大金钱。
递归三部曲
- 确定递归函数的参数和返回值
长度为2的dp数组
dp[0]0记录不偷该节点所得到的的最大金钱,dp[1]1记录偷该节点所得到的的最大金钱。 - 确定终止条件
在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回 - 确定遍历顺序
首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。 - 确定单层递归的逻辑
如果是偷当前节点,那么左右孩子就不能偷,val1 = cur->val + left[0] + right[0]; (如果对下标含义不理解就再回顾一下dp数组的含义)
如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);
最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱} - 举例推导dp数组
// 动态规划
class Solution {public int rob(TreeNode root) {int[] res = robAction(root);return Math.max(res[0], res[1]);}int[] robAction(TreeNode root){int res[] = new int[2]; // res[0] 代表不偷时的价值 res[1]代表偷的时候的价值// 终止递归条件if(root == null){return res;}// 后序遍历// 左右int[] left = robAction(root.left);int[] right = robAction(root.right);// 中res[0] = Math.max(left[0], left[1]) +Math.max(right[0], right[1]);res[1] = root.val + left[0] + right[0];return res;}
}
相关文章:

代码随想录算法训练营第52天(动态规划09 ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
动态规划part09 198.打家劫舍解题思路 213.打家劫舍II解题思路 337.打家劫舍III解题思路 今天就是打家劫舍的一天,这个系列不算难,大家可以一口气拿下。 198.打家劫舍 题目链接: 198.打家劫舍 视频讲解: 198.打家劫舍 文章讲解&…...
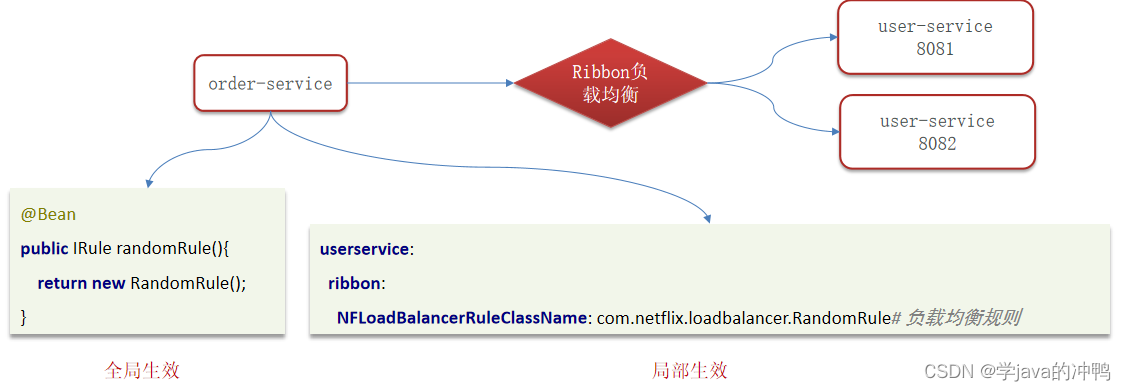
微服务篇之负载均衡
一、Ribbon负载均衡流程 二、Ribbon负载均衡策略 1. RoundRobinRule:简单轮询服务列表来选择服务器。 2. WeightedResponseTimeRule:按照权重来选择服务器,响应时间越长,权重越小。 3. RandomRule:随机选择一个可用的服…...
 + egl + opengles 使用FBO渲染到纹理实例(六))
wayland(xdg_wm_base) + egl + opengles 使用FBO渲染到纹理实例(六)
文章目录 前言一、FBO介绍1. FBO 简介2. FBO的关键组成部分3. FBO的基本工作流程4. FBO 实现渲染到纹理5. FBO 实现离屏渲染二、FBO 实现渲染到纹理的代码实例1. egl_wayland_texture3_2.c2. xdg-shell-client-protocol.h 和 xdg-shell-protocol.c3. 编译4. 运行总结参考资料前…...

基于 RisingWave、Instaclustr 和 Apache Superset 对维基百科实时监控
得益于 RisingWave 和 Kafka 等流处理工具, 数据工程师能实时洞察流数据中的重要信息。这能够助力制定决策,并在多个层面改善用户体验,包括推荐系统、金融、物流、汽车、制造业、 IIOT 设备和零售。 在这篇博客中,我们会把 Risin…...

建站用帝国CMS好还是WordPress好
随着互联网的迅猛发展,内容管理系统(CMS)在网站建设中扮演着越来越重要的角色。在众多CMS中,帝国CMS和WordPress因其强大的功能和广泛的用户基础而备受关注。本文将对这两种CMS进行详细比较,分析它们的优势与不足,以便用户能够根据…...
—图》)
深度学习基础之《TensorFlow框架(2)—图》
一、什么是图结构 1、图包含了一组tf.Operation代表的计算单元对象和tf.Tensor代表的计算单元之间流动的数据 图结构:数据(Tensor) 操作(Operation) 二、图相关操作 1、默认图 通常TensorFlow会默认帮我们创建一张图 查看默认图的两种方法: &#x…...

Web3区块链游戏:创造虚拟世界的全新体验
随着区块链技术的不断发展,Web3区块链游戏正逐渐崭露头角,为玩家带来了全新的虚拟世界体验。传统游戏中的中心化结构和封闭经济体系已经被打破,取而代之的是去中心化的游戏环境和真实所有权的数字资产。本文将深入探讨Web3区块链游戏的特点、…...

单机启动/开机启动SpringBoot服务的正确方式
此操作只针对于测试环境或单机部署的情况下,使用Jenkins自动化部署或docker部署SpringBoot服务请忽略。 SpringBoot单机启动和集群启动的区别: 部署方式:单机启动可以直接运行jar文件或使用IDE启动应用程序,而双机集群启动需要将…...

[C#]winform基于opencvsharp结合CSRNet算法实现低光图像增强黑暗图片变亮变清晰
【算法介绍】 "Conditional Sequential Modulation for Efficient Global Image Retouching" 是一种图像修饰方法,主要用于对图像进行全局的高效调整。该方法基于深度学习技术,通过引入条件向量来实现对图像特征的调制,以达到改善…...

抓包分析 TCP 协议
TCP 协议是在传输层中,一种面向连接的、可靠的、基于字节流的传输层通信协议。 环境准备 对接口测试工具进行分类,可以如下几类: 网络嗅探工具:tcpdump,wireshark 代理工具:fiddler,charles&…...

代码随想录算法训练营day27 | 93.复原IP地址、78.子集、90.子集II
93.复原IP地址 和C不同,使用列表存储已经分割的数据,而不是直接操作字符串。为了使用这个列表搞了老久,主要问题出在,在判断终止条件的时候,path也需要回溯一下 class Solution:def __init__(self):self.result []s…...

RuntimeError: CUDA out of memory.【多种场景下的解决方案】
RuntimeError: CUDA out of memory.【多种场景下的解决方案】 🌈 个人主页:高斯小哥 🔥 高质量专栏:【Matplotlib之旅:零基础精通数据可视化】 🏆🏆关注博主,随时获取更多关于深度学…...

LeetCode刷题| Leetcode 45. 跳跃游戏,1190. 反转每对括号间的子串,781. 森林中的兔子,739. 每日温度
45. 跳跃游戏 题目链接: 45. 跳跃游戏 II - 力扣(LeetCode) 思路:这道题思路不难记,遍历数组每个位置,更新下一次的范围,当当前位置已经在当前范围之外时,步数一定得加一ÿ…...
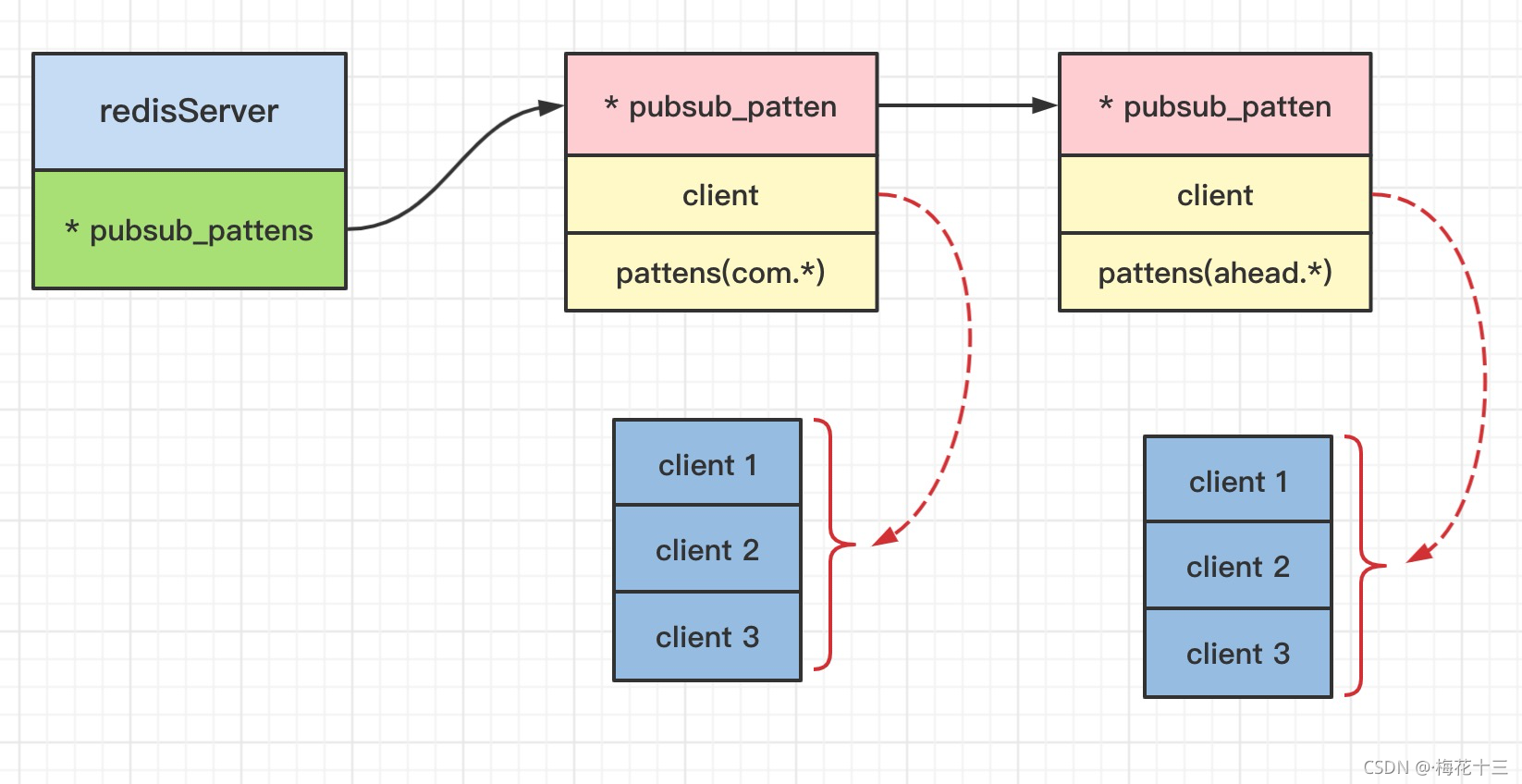
Redis(03)——发布订阅
基础命令 基于频道 publish channel message:将信号发送到指定的频道pubsub subcommand [argument [argyment]]:查看订阅或发布系统状态subscribe channel [channel]:订阅一个或多个频道的信息unsubscribe [channel [channel]]:退…...
⭐北邮复试刷题LCR 034. 验证外星语词典__哈希思想 (力扣119经典题变种挑战)
LCR 034. 验证外星语词典 某种外星语也使用英文小写字母,但可能顺序 order 不同。字母表的顺序(order)是一些小写字母的排列。 给定一组用外星语书写的单词 words,以及其字母表的顺序 order,只有当给定的单词在这种外…...
)
ECMAScript 6+ 新特性 ( 二 )
2.12. class类 ES6 提供了更接近传统语言的写法,引入了 Class(类)这个概念,作为对象的模板。通过 class 关键字,可以定义类。 ES6 的 class 可以看作只是一个语法糖,它的绝大部分功能ES5 都可以做到&…...

JS游戏项目合集【附源码】
文章目录 一:迷宫小游戏二:俄罗斯方块三:压扁小鸟 一:迷宫小游戏 【迷宫游戏】是一款基于HTML5技术开发的游戏,玩法简单。玩家需要在一个迷宫中找到出口并成功逃脱,本项目还有自动寻路(Track&a…...

React中hooks使用限制及保存函数组件状态
React Hooks 的限制主要有两条: 不要在循环、条件或嵌套函数中调用 Hook; 在 React 的函数组件中调用 Hook。 首先,Hooks是一个对象,大致结构如下: const hook: Hook {memoizedState: null,baseState: null,baseQ…...

用git命令来上传项目到GitHub我自己的仓库
目录 在GitHub上创建仓库并使用git命令上传到仓库的步骤如下: 其他操作 怎么退出git/COMMIT_EDITMSG [unix] 相关报错 error: src refspec main does not match any error: failed to push some refs to https://github.com/Liu22Jun16Liang/MyQt error: fail…...

.NET有哪些微服务框架
1.概述 想要对.net的微服务方案进行一下调查,看有什么可选的方案和框架,与spring clound相比.net 创建微服务是相对较麻烦的。 ID名称说明1Service FabricSteeltoe是帮助.NET开发的服务接入Spring Cloud技术栈的官方支持工具。也就是说,微服…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
