【递归】:原理、应用与案例解析 ,助你深入理解递归核心思想
递归
1.基础简介
递归在计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集
例如 递归遍历环形链表
- 基本情况(Base Case):基本情况是递归函数中最简单的情况,它们通常是递归终止的条件。在基本情况下,递归函数会返回一个明确的值,而不再进行递归调用。
- 递归情况(Recursive Case):递归情况是递归函数中描述问题规模较大的情况。在递归情况下,函数会调用自身来解决规模更小的子问题,直到达到基本情况。
优点
- 简洁清晰:递归能够将复杂的问题简化成更小的子问题,使得代码更加清晰易懂。
- 问题建模:递归能够自然地将问题建模成递归结构,使得问题的解决变得更加直观。
- 提高代码复用性:通过递归,可以在不同的情景中复用相同的解决方案。
缺点
- 性能损耗:递归调用涉及函数的重复调用和堆栈的频繁使用,可能会导致性能下降。
- 内存消耗:每次递归调用都需要在堆栈中存储函数的调用信息,可能会导致堆栈溢出的问题。
- 难以理解和调试:复杂的递归调用可能会导致代码的难以理解和调试,特别是递归函数中存在多个递归调用时。
常用场景
- 树和图的遍历:树和图的结构天然适合递归的处理方式,如深度优先搜索(DFS)。
- 分治算法:许多分治算法,如归并排序和快速排序,都是通过递归实现的。
- 动态规划:动态规划问题中,递归可以帮助描述问题的递归结构,但通常需要使用记忆化搜索或者自底向上的迭代方式来提高性能。
- 排列组合问题:许多排列组合问题,如子集、组合、排列等,可以通过递归实现。
/*** 递归进行遍历* @param node 下一个节点* @param before 遍历前执行的方法* @param after 遍历后执行的方法* @deprecated 递归遍历,不建议使用,递归深度过大会导致栈溢出。建议使用迭代器,或者循环遍历,或者使用尾递归,或者使用栈* @see #loop(Consumer, Consumer)*/
public void recursion(Node node, Consumer<Integer> before, Consumer<Integer> after){// 表示链表没有节点了,那么就退出(注意 环形链表的 末尾 不是null 而是头节点)if (node == sentinel){return;}// 反转位置就是逆序了before.accept(node.value);recursion(node.next, before, after);after.accept(node.value);
}
- 自己调用自己,说明每一个函数对应着一种解决方案,自己调用自己意味着解决方案是一样的或者说是有规律的
- 每次调用,函数处理的数据相对于上一次会缩减,而且最后会缩减至无需继续递归
- 内层函数调用(子集处理完成),外层函数才能调用完成
1.1.思路
首先需要确定自己的问题,能不能用递归的思路去解决
然后需要推导出递归的关系,父问题和子问题之间的关系, 以及递归的中止条件
f ( n ) = { 停止 , n = n u l l f ( n , n e x t ) , n ≠ n u l l f(n) = \begin{cases} 停止&, n = null \\ f(n,next)&, n \neq null \\ \end{cases} f(n)={停止f(n,next),n=null,n=null
- 深入到最里层的 叫做递
- 从最里层出来的叫做归
- 在递过程中,外层函数内的局部变量(以及参数方法)并未消失,归的时刻还会用到。
2.案例
2.1.案例1-求阶乘
@Test
@DisplayName("测试-递归-阶乘")
public void test1(){int factorial = factorial(5);logger.error("factorial :{}",factorial);
}/*** 阶乘* @param value 阶乘的值* @return 阶乘的结果*/
public int factorial(int value){// 递归的终止条件if(value ==1){return 1;}// 递归的公式 f(n) = n * f(n-1)return value * factorial(value-1);
}

2.2.案例2-字符串反转
- 递:n从0开始,每次都从都头部对字符串进行分割,每次拼接的字符串只取第一位
- 归:从 str.length() == 1开始归,从归开始拼接,自然是逆序的
# 思路递归的终止条件是字符串的长度为1, 递归的公式是 f(n) = f(n-1) + str.charAt(0) 从后往前拼接字符串
/*** 反向打印字符串序列* @param str 字符串* @return 反向打印的字符串*/
public String reverse(String str){if(str.length() == 1){return str;}logger.error("str.substring(1) = {} , str.CharArt(0) = {}",str.substring(1),str.charAt(0));// substring(1) 从下标为1的位置开始截取字符串, chatAt(0) 获取下标为0的字符return reverse(str.substring(1)) + str.charAt(0);
}@Test
@DisplayName("测试-递归-反向打印字符串序列")
public void test2(){String str = "abcdefg";String reverse = reverse(str);logger.error("reverse :{}",reverse);
}

2.3.案例3-递归二分查找
/*** 二分查找* @param source 原始数组* @param target 目标值* @param left 左边界* @param right 右边界* @return 目标值的索引位置*/public int binaryFind(int source[],int target,int left,int right){// 先找到中间值int mid = (left + right) >>> 1;if (left > right){// 如果left > right 直接返回-1return -1;}if (source[mid] < target){// 如果中间值小于目标值,则在右边进行寻找return binaryFind(source,target,mid+1,right);} else if(source[mid] > target){// 如果中间值大于目标值 则在左边进行寻找return binaryFind(source,target,left,mid-1);} else {// 如果中间值等于目标值,则返回索引位置return mid;}}/*** 二分查找* @param source 原始数组* @param target 目标值* @return 目标值的索引位置*/public int search(int[] source,int target){// 二分查找 递归的终止条件是 left > rightreturn binaryFind(source,target,0,source.length-1);}@Test@DisplayName("测试-递归-二分查找")public void test3(){int[] source = {1,2,3,4,5,6,7,8,9,10};int target = 3;int index = search(source,target);logger.error("index :{}",index);}

2.4.案例4-递归冒泡排序
递归冒泡排序原理:
递归冒泡排序是一种排序算法,它将数组分成已排序和未排序两部分。通过递归地比较相邻元素并交换它们的位置,每次递归都将未排序部分的最大元素移到已排序部分的末尾,直到整个数组有序。
实现思路:
- 初始化:将整个数组视为未排序部分。
- 递归调用:递归地调用
bubble_sort()函数来处理未排序部分,直到未排序部分长度为0或1,排序结束。 - 比较与交换:在每次递归中,从数组开始处向后遍历,比较相邻元素。如果前一个元素大于后一个元素,则交换它们的位置。
- 更新未排序部分:记录每次交换的位置,即最后一次交换的索引,作为下一次递归的边界,确保下一次递归只需处理未排序部分的子数组。
- 终止条件:递归终止条件是未排序部分长度为0或1,表示数组已排序完成。
可优化的地方及优势:
- 优化点:递归冒泡排序在每次递归中,对未排序部分进行了全遍历,可能导致效率较低,尤其是对于大型数组。
- 优势:递归冒泡排序的主要优势在于其简洁易懂的实现方式,易于理解和实现。
实现突出重点:
- 递归调用:通过递归调用
bubble_sort()函数,将排序过程分解为子问题,直到基本情况(未排序部分长度为0或1)得到解决。 - 边界更新:每次递归后,更新未排序部分的边界,使下一次递归只需处理未排序部分的子数组。
- 终止条件:设定递归终止条件,确保排序过程能够正确结束。
# 思路比较相邻的元素。如果第一个比第二个大,就交换他们两个。对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。针对所有的元素重复以上的步骤,除了最后一个。持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
# 控制1(递归)每次重新划分排序的区间,负责把已经排序的区间进行过滤2(循环)负责两两比较交换。


/*** 递归冒泡排序* <ul>* <li>将数组划分成两部分,[0,j] [j+1,length - 1]</li>* <li>[0,j] 左边是未排序的部分</li>* <li>[j+1,length - 1] 右边是已经排序的部分</li>* <li>在未排序的区间内,相邻的两个元素比较,如果前一个元素大于后一个元素,那么交换位置</li>** </ul>* @param source*/public void sort (int [] source){bubble_sort(source,source.length-1);}/*** 递归冒泡排序* @param source 待排序的数组* @param j 未排序的区间的起始位置*/public void bubble_sort(int [] source,int j){// 递归的终止条件是数组的长度为1 或者数组的长度为0if (j == 0){return;}// x充 未排序 和已经排序的分界线int x = 0;// 每次都是从0开始for (int i = 0; i < j;i++){// 如果前一个元素比后一个元素大,那么交换位置if (source[i] > source[i+1]){int temp = source[i];source[i] = source[i+1];source[i + 1] = temp;x = i;}}// 递归调用(因为每次最大值都会移动到最后,所以每次的排序区间都往前进行移动)bubble_sort(source,x-1);}@Test@DisplayName("测试-递归-冒泡排序")public void test4(){int[] source = {4,3,2,1,5,6,7};sort(source);logger.error("source :{}",source);}

2.5.案例5-插入排序
插入排序原理:
插入排序是一种直观的排序算法,类似于整理扑克牌。它从未排序的部分选取元素,并将其插入到已排序的序列中,直到所有元素都排好序为止。
实现思路:
这段代码使用递归来实现插入排序。在递归函数 insertion() 中,每次调用时,它从未排序的部分选择第一个元素 t = source[low],然后将其插入到已排序的序列中的适当位置。
具体实现过程如下:
- 从右向左遍历已排序的部分,找到第一个比待插入元素小的位置。
- 将比待插入元素大的元素往后移一位,为待插入元素腾出空间。
- 插入待排序元素到找到的位置,插入位置为
i + 1,其中i是最后一个比待插入元素小的元素的下标。
递归终止条件:
递归的终止条件是当 low 等于数组长度时,表示所有元素都已处理完成,无需继续排序。


/*** 插入排序* @param source 原始数组*/
public void insert_sort(int[]source){// 递归调用插入排序 low 从1开始insertion(source,1);
}/*** 插入排序* @param source 原始数组* @param low 未排序数据的起始位置*/
private void insertion(int[]source,int low){// 递归的终止条件是 low == source.lengthif(low == source.length){return;}// 存储临时变量 (存放low指向的数据)int t = source[low];// 已经排序区域的指针int i = low -1;// 从右往左找,只要找到第一个比t小的就能确认插入位置while (i >=0 && source[i] > t ){// 如果没有找到插入位置 一直循环// 空出插入位置source[i+1] = source[i];i--;}// 找到了插入位置// 将t赋值给i +1 的位置就行了source[i + 1] = t;insertion(source,low + 1);}@Test
@DisplayName("测试-递归-插入排序")
public void test5(){int[] source = {2,4,5,10,7,1};insert_sort(source);logger.error("source :{}",source);
}
多路递归
2.案例1-斐波那契数列
- 每个递归只包含一个自身的调用,称之为single recursion
- 如果每个递归函数包含多个自身的调用称为multi recursion
f ( n ) = { 0 , n = 0 1 , n = 1 f ( n − 1 ) + f ( n − 2 ) , n > 1 f(n) = \begin{cases} 0&, n = 0 \\ 1&, n = 1 \\ f(n-1)+f(n-2)&, n > 1 \\ \end{cases} f(n)=⎩ ⎨ ⎧01f(n−1)+f(n−2),n=0,n=1,n>1
@Test@DisplayName("测试-递归-斐波那契数列")public void test1(){int factorial = factorial(10);logger.info("factorial:{}",factorial);}/*** 斐波那契数列* @param n 传入的参数* @return 返回的结果*/public int factorial(int n){// 递归的出口,当n为0时,返回0,当n为1或者2时,返回if (n == 0){return 0;}if (n == 1 || n == 2){return 1;}// 依次往下递归return factorial(n-1) + factorial(n -2);}

递归爆栈
1.分析
在Java中,递归爆栈是指递归调用导致调用栈溢出的情况。在解释递归爆栈时,我们可以涉及到Java的内存模型和变量存储位置的分析。
1.1 Java 内存模型:
Java程序在运行时,内存被划分为不同的区域,其中涉及到:
- 堆(Heap):用于存储对象实例,由Java垃圾回收器进行管理和清理。
- 栈(Stack):每个线程都有自己的栈,用于存储局部变量、方法调用和部分对象引用。
- 方法区(Method Area):存储类的结构信息、静态变量、常量等。
- 程序计数器(Program Counter):记录线程执行的当前位置。
1.2. 递归的内存分析:
在Java中,每次方法调用都会在栈上分配一定的空间,包括方法的参数、局部变量和返回地址。当一个方法被调用时,会将当前方法的上下文(包括参数、局部变量等)推入栈中,当方法执行结束时,栈顶的帧会被弹出。
1.3. 递归爆栈的原因:
递归函数在调用自身时,会持续地将新的调用帧推入栈中,如果递归调用的深度过大,栈空间会耗尽,导致栈溢出错误。
1.4. 变量存储位置分析:
- 局部变量(Local Variables):在方法执行时,局部变量存储在栈帧中,并且随着方法的结束而被销毁。
- 实例变量(Instance Variables):实例变量存储在对象的堆内存中,随着对象的创建和销毁而分配和释放。
- 静态变量(Static Variables):静态变量存储在方法区中,它们在类加载时被初始化,在程序结束时销毁。
2.代码
/*** 递归求和* @param n 传入的参数* @return 返回的结果*/
public int add(int n){if (n == 1){return 1;}return add(n -1) + n;
}@Test
@DisplayName("测试-递归-递归求和")
public void test2(){int sum = add(11111110);logger.error("sum:{}",sum);
}

3.解决
# 目前只有C++ 和 scala 能针对尾递归优化,所以我们一般需要将递归转为循环来写
- 尾调用
// 如果函数的最后一步,是调用一个函数,那么成为尾调用
function a(){return b();
}// 下面这个 三段代码并不能称为尾调用
function a(){// 虽然调用了函数,但是又用到了外层函数的数值1return b() + 1;
}function a(){// 最后异步并非调用函数const c = b() + 1return c;
}function a(x){// 虽然调用了函数,但是又用到了外层函数的数值xreturn b() + x;
}
4.总结
递归爆栈的问题通常发生在递归调用的深度过大时,导致栈空间耗尽。通过合理控制递归调用深度、优化算法或者考虑使用迭代等方法可以避免这类问题,在Java中,局部变量和方法调用的栈帧管理是导致递归爆栈的关键因素之一。
递归是一种强大的问题解决工具,能够简化问题、提高代码的清晰度和可读性。然而,在使用递归时,需要注意避免潜在的性能问题和堆栈溢出问题。选择适当的场景和合适的算法,可以充分发挥递归的优势,提高程序的效率和可维护性。
相关文章:

【递归】:原理、应用与案例解析 ,助你深入理解递归核心思想
递归 1.基础简介 递归在计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集 例如 递归遍历环形链表 基本情况(Base Case):基本情况是递归函数中最简单的情况,它们通常是递…...
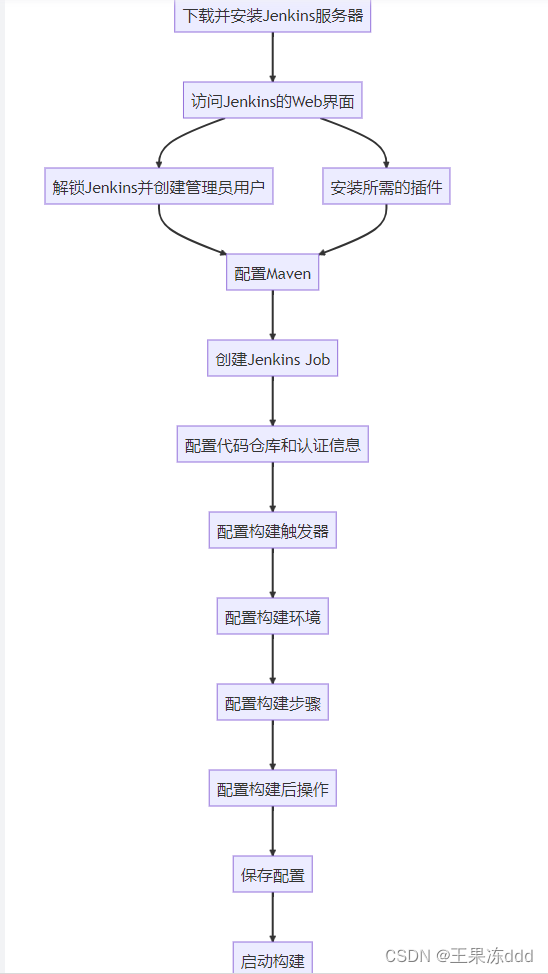
【 Maven 】花式玩法之多模块项目
目录 一、认识Maven多模块项目 二、maven如何定义项目的发布策略 2.1 版本管理 2.2 构建配置 2.3 部署和发布 2.4 依赖管理 2.5 发布流程 三、使用Jenkins持续集成Maven项目 四、总结 如果你有一个多模块项目,并且想将这些模块发布到不同的仓库或目标位置&…...

LeetCode 热题 100 Day01
哈希模块 哈希结构: 哈希结构,即hash table,哈希表|散列表结构。 图摘自《代码随想录》 哈希表本质上表示的元素和索引的一种映射关系。 若查找某个数组中第n个元素,有两种方法: 1.从头遍历,复杂度…...
[vscode]vue js部分结尾加分号
设置中寻找 semicolons确定在TypeScript的这个扩展中设置选项为insert...
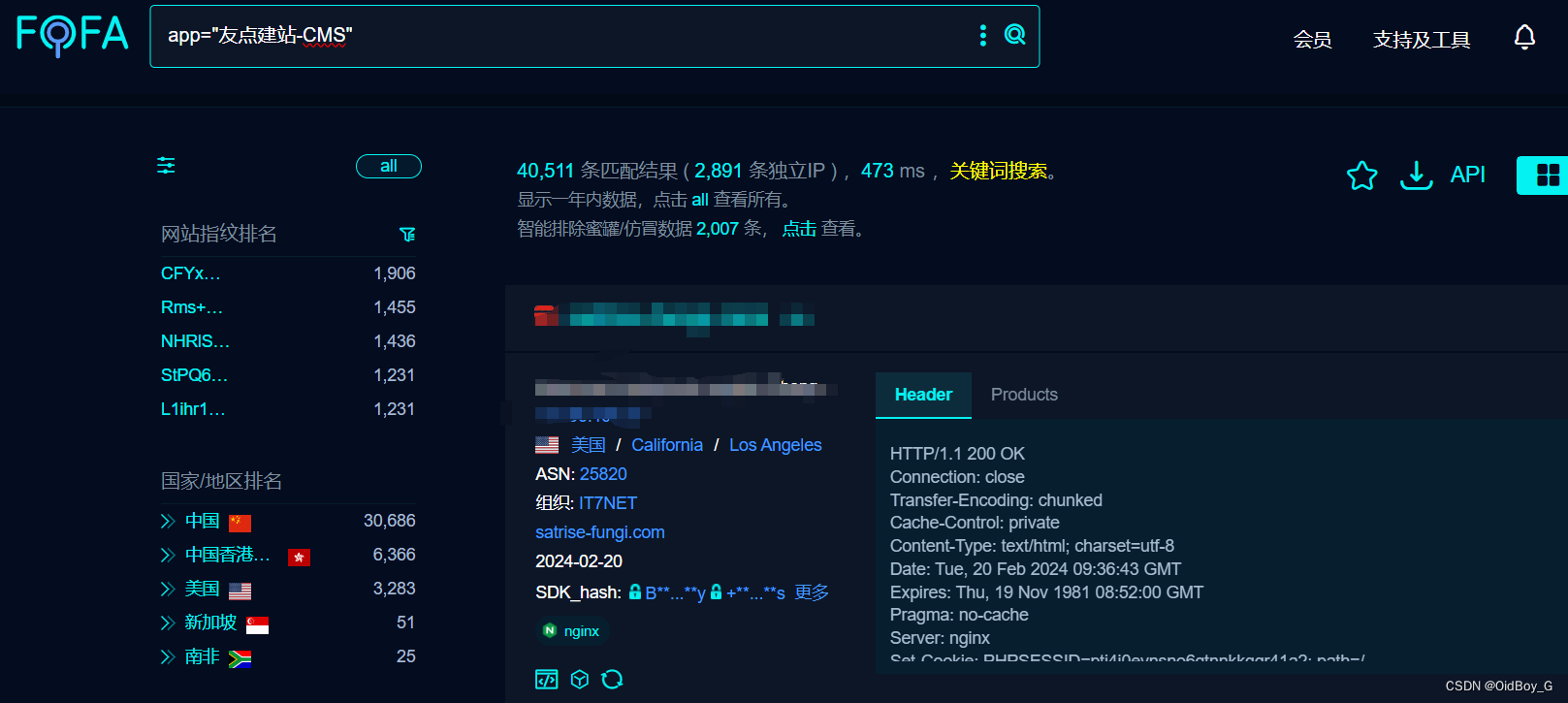
友点CMS image_upload.php 文件上传漏洞复现
0x01 产品简介 友点CMS是一款高效且灵活的网站管理系统,它为用户提供了简单易用的界面和丰富的功能。无论是企业还是个人,都能通过友点CMS快速搭建出专业且美观的网站。该系统支持多种内容类型和自定义模板,方便用户按需调整。同时,它具备强大的SEO功能,能提升网站在搜索…...

C语言—指针(3)
嘿嘿嘿嘿,你看我像指针吗? 不会写,等我啥时候会写了再说吧,真的累了,倦了 1.面试题 1)定义整形变量i; 2)p为指向整形变量的指针变量; 3)定…...
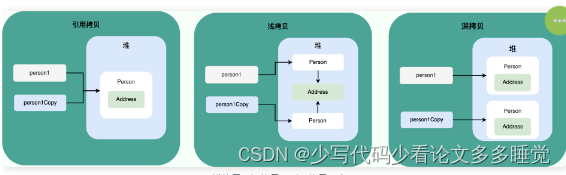
【八股文】面向对象基础
【八股文】面向对象基础 面向对象和面向过程的区别 面向过程把解决问题的过程拆成一个个方法,通过一个个方法的执行解决问题。面向对象会先抽象出对象,然后用对象执行方法的方式解决问题。 创建一个对象用什么运算符?对象实体与对象引用有何不同? …...

Day49 647 回文子串 516 最长回文子序列
647 回文子串 给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。 具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。 方法一:动态规划: 采用一个二维的dp数组…...

探秘GNU/Linux Shell:命令行的魔法世界
GNU/Linux的Shell是一种特殊的交互式工具,为用户提供了强大的控制和管理Linux系统的方式。在这个博客中,我们将深入了解Shell的基本概念、功能以及不同类型的Shell。 Shell的本质 Shell的核心是命令行提示符,它是用户与Linux系统进行交互的…...
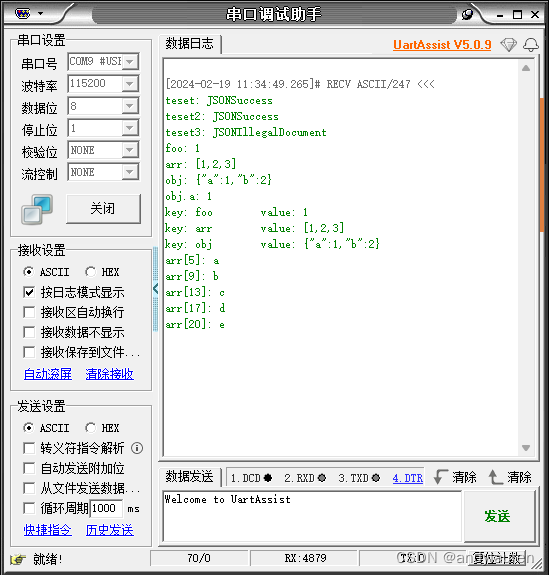
基于STM32F407的coreJSON使用教程
目录 概述 工程建立 代码集成 函数介绍 使用示例 概述 coreJSON是FreeRTOS中的一个组件库,支持key查找的解析器,他只是一个解析器,不能生成json数据。同时严格执行 ECMA-404 JSON 标准。该库用 C 语言编写,设计符合 ISO C90…...
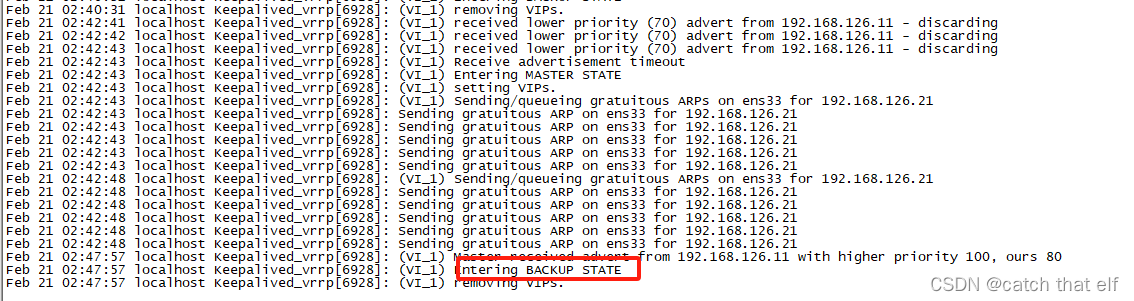
keepalived双主模式测试
文章目录 环境准备部署安装keepavlived配置启动测试模拟Nginx宕机重新启动问题分析 环境准备 测试一下keepalived的双主模式,所谓双主模式就是两个keepavlied节点各持有一个/组虚IP,默认情况下,二者互为主备,同时对外提供服务&am…...

微服务中的熔断、降级和限流
在现代微服务架构中,熔断、降级和限流是保障系统稳定性和可靠性的重要手段。本文将深入探讨这三种机制在微服务架构中的作用、原理以及实践方法。 1. 熔断(Circuit Breaker) 1.1 作用和原理 熔断器是一种可以在服务发生故障时快速中断请求的机制,防止故障蔓延到整个系统…...

2023年便宜的云服务器分享:最低26元4核16G
2024年阿里云服务器租用价格表更新,云服务器ECS经济型e实例2核2G、3M固定带宽99元一年、ECS u1实例2核4G、5M固定带宽、80G ESSD Entry盘优惠价格199元一年,轻量应用服务器2核2G3M带宽轻量服务器一年61元、2核4G4M带宽轻量服务器一年165元12个月、2核4G服…...

汽车零部件制造业MES系统解决方案
一、汽车零部件行业现状 随着全球汽车产业不断升级,汽车零部件市场竞争日趋激烈,从上游的钢铁、塑料、橡胶等生产到下游的主机厂配套制造,均已成为全球各国汽车制造大佬战略目标调整的焦点,其意欲在汽车零部件行业快速开疆扩土&…...

区块链/加密币/敏感/特殊题材专供外媒发稿,英文多国语言海外新闻营销推广
【本篇由言同数字科技有限公司原创】敏感题材是海外媒体在报道过程中常遇到的难题,需要平衡新闻真实性、公正性与敏感性。本文将探讨海外媒体报道敏感题材所面临的挑战,并介绍如何抓住机遇提高报道质量。 第一部分:敏感题材报道的挑战 报道…...

初识Nginx
摘要:最近几个项目中的接口总是访问受限,需要后端同事配置Nginx代理,了解下Nginx后面自己配置。 Nginx 是一款高性能的开源 Web 服务器和反向代理服务器。它具有轻量级、高并发、低内存消耗等特点,常被用作静态资源服务、负载…...

Rust语言之多线程
文章目录 一、简介二、创建线程1.创建一个线程2.创建多个线程生成随机数尝试让程序睡一会儿引入多线程 三、线程返回值的处理1.每个线程处理一个独立的值2.多个线程处理一个值Arc(原子引用计数)Mutex(互斥锁)RwLock(读…...

现有的通用模型中融入少量中文数据没有太大意义少量的数据就能影响整个大模型
相关链接:只修改一个关键参数,就会毁了整个百亿参数大模型? | 新程序员-CSDN博客 现象 1:mBERT 模型的跨语言迁移 现象 2:大语言模型同样存在显著的语言对齐 现象 3:知识与语言分离 现象 4:…...
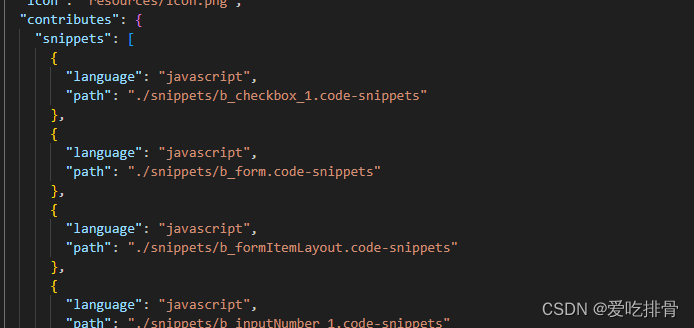
vscode 开发代码片段插件
环境准备 node - 20v版本 ,推荐使用nvm进行版本控制全局安装 "yo" 是 Yeoman 工具的命令行工具, npm i yo -g全局安装 generator-code 是一个 Yeoman 脚手架 gernerator-code npm i gernerator-code -g全局安装 npm install -g vsce官方文档 …...

算法竞赛STL:array的使用方法
算法竞赛STL:array的使用方法 文章目录 算法竞赛STL:array的使用方法array array 容器描述: array是一种固定大小的容器,它包含指定数量的元素。每个元素都有一个非负整数索引,用于访问或修改它。 使用方法ÿ…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
