数据结构——时间复杂度
前言:
当谈到数据结构和算法时,时间复杂度是一个至关重要的概念。时间复杂度是衡量算法执行时间随输入规模增长而变化的度量,它指示了算法的效率和性能。在本篇博客中,我们将深入探讨时间复杂度的相关知识,并结合C语言给出一些代码示例来帮助读者更好地理解这一概念。
目录
1. 什么是时间复杂度?
2. 时间复杂度的分类
3. 时间复杂度的计算方法
O(1):常数时间复杂度
O(n):线性时间复杂度
O(n^2):平方时间复杂度
4. 总结
1. 什么是时间复杂度?
时间复杂度是一种描述算法执行时间随着输入规模增长而变化的度量。它用大O符号(O)来表示,表示算法执行时间的上界。时间复杂度描述的是算法执行时间与输入规模的增长趋势,而不是具体的执行时间。因此,时间复杂度是一种抽象的度量,用来评估算法的效率。
(大O符号代表的是大O表示法,这是一种粗略的统计方法,例如O(n*n+n)用大O表示法实际上表示为O(n*n),因为当n足够大的时候,n相对于n*n是可以忽略的。
2. 时间复杂度的分类
在数据结构和算法中,我们通常会遇到以下几种常见的时间复杂度:
- O(1):常数时间复杂度,表示算法的执行时间不随输入规模的增长而变化,是最理想的情况。
- O(log n):对数时间复杂度,通常出现在二分查找等分治算法中。
- O(n):线性时间复杂度,表示算法的执行时间与输入规模成正比。
- O(n log n):线性对数时间复杂度,通常出现在快速排序、归并排序等分治算法中。
- O(n^2):平方时间复杂度,通常出现在嵌套循环的算法中。
- O(2^n):指数时间复杂度,通常出现在递归算法中。
3. 时间复杂度的计算方法
在分析算法的时间复杂度时,我们通常关注算法中执行次数最多的那部分代码(代码的核心部分)。通过分析算法中基本操作的执行次数,并根据输入规模的增长情况确定时间复杂度。
下面通过C语言的代码示例来说明不同时间复杂度的计算方法:
O(1):常数时间复杂度
#include <stdio.h>int main() {int a = 10;int b = 20;int sum = a + b;printf("Sum: %d\n", sum);return 0;
}在上面的代码中,无论a和b的值如何变化,计算sum的操作都只执行一次,因此时间复杂度为O(1)。
注:只要执行次数为常数次,即能数的过来,都表示成O(1).
O(n):线性时间复杂度
#include <stdio.h>int main() {int n = 10;for (int i = 0; i < n; i++) {printf("%d ", i);}return 0;
}在上面的代码中,for循环的执行次数与n的大小成正比,因此时间复杂度为O(n)。
注:一般时间复杂度为O(n)的都是代码中有单层循环的。
O(n^2):平方时间复杂度
#include <stdio.h>int main() {int n = 5;for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {printf("(%d, %d) ", i, j);}}return 0;
}在上面的代码中,嵌套的两个for循环的执行次数与n的平方成正比,因此时间复杂度为O(n^2)。
注:一般时间复杂度为O(n^2)的都是代码中有循环嵌套的。
4. 总结
时间复杂度是评估算法效率的重要指标,通过分析算法中基本操作的执行次数来确定。在实际编程中,了解不同时间复杂度对算法性能的影响,能够帮助我们设计出更加高效的算法。通过本篇博客的介绍和代码示例,相信读者对时间复杂度有了更深入的理解。
希望本篇博客能够帮助读者更好地理解时间复杂度的相关知识,并在日常编程中更加灵活地运用这一概念。如果有任何疑问或者需要进一步的解释,请随时留言,我将尽力为您解答。感谢阅读!此外,鉴于本人水平有限,文中若有不足还请见谅并指出错误,给本人一个挽救的机会。
创作不易,还请一键三连。
相关文章:

数据结构——时间复杂度
前言: 当谈到数据结构和算法时,时间复杂度是一个至关重要的概念。时间复杂度是衡量算法执行时间随输入规模增长而变化的度量,它指示了算法的效率和性能。在本篇博客中,我们将深入探讨时间复杂度的相关知识,并结合C语言…...

《剑指Offer》笔记题解思路技巧优化 Java版本——新版leetcode_Part_5
《剑指Offer》笔记&题解&思路&技巧&优化_Part_5 😍😍😍 相知🙌🙌🙌 相识😢😢😢 开始刷题🟢1. LCR 158. 库存管理 II——数组中出现次数超过一…...

ubuntu上安装docker
在 Ubuntu 上安装 Docker,可以按照以下步骤进行操作: 更新软件包列表:运行以下命令来更新系统的软件包列表: sudo apt update安装必要的依赖项:运行以下命令来安装 Docker 所需的依赖项: sudo apt install …...

【Docker】Linux主机部署Docker
Docker部署 1.二进制文件部署 到如下地址,下载二进制包。 Docker官网:https://docs.docker.com/engine/install/binaries/ 网易镜像源:https://mirrors.163.com/docker-ce/linux/static/stable/x86_64/ 下载好的二进制包上传到主机…...

vue前端docx库生成word表格 并合并单元格的例子
Vue.js 是一个流行的前端JavaScript框架,用于构建用户界面和单页应用程序。在Vue中生成Word表格并合并单元格,通常需要使用额外的库,如docx,它是一个用于创建和修改Word文档(.docx)的JavaScript库。 …...

FastGPT配置文件及OneAPI程序:
FastGPT配置文件及OneAPI程序:百度网盘 请输入提取码 提取码:wuhe 创建fastgpt目录:mkdir fastgpt 切换到fastgpt目录:cd fastgpt 下载docker-compose文件:curl -O https://raw.githubusercontent.com/labring/Fast…...
Positive Semidefinite Matrices 什么是半正定矩阵?(undone)
参考视频:https://www.bilibili.com/video/BV1Vg41197ew/?vd_source7a1a0bc74158c6993c7355c5490fc600 参考资料(半正定矩阵的定义):https://baike.baidu.com/item/%E5%8D%8A%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/2152711?frge_ala 看看半正定矩阵的…...

shapely 笔记:STR TREE
数据结构笔记:R树-CSDN博客 1 基本介绍 使用Sort-Tile-Recursive (STR) 算法创建的仅查询的R-tree空间索引该树索引每个几何图形的边界框。树在初始化时直接构建,且一旦创建后不能添加或移除节点所有操作返回输入几何图形的索引边界框限于二维并且是轴…...

neo4j常用代码
1】查版本: CALL dbms.components() YIELD name, versions RETURN name, versions; 2】清数据: MATCH ()-[r]->() DELETE r; MATCH (n) DETACH DELETE n; 3】NEO4J 操作入门_neo4j查看历史执行命令-CSDN博客 :play --首页 :help match/keys/com…...

OpenAI划时代大模型——文本生成视频模型Sora作品欣赏(五)
Sora介绍 Sora是一个能以文本描述生成视频的人工智能模型,由美国人工智能研究机构OpenAI开发。 Sora这一名称源于日文“空”(そら sora),即天空之意,以示其无限的创造潜力。其背后的技术是在OpenAI的文本到图像生成模型DALL-E基础上开发而成的。模型的训练数据既包含公开…...

Less预处理器教程
学习源码可以看我的个人前端学习笔记 (github.com):qdxzw/frontlearningNotes 觉得有帮助的同学,可以点心心支持一下哈 一、Less介绍 less官方文档 lesscss.org/ less中文文档 less.bootcss.com/ less是一种css预处理器,它扩展了css语言,…...

PCL 计算点云AABB包围盒的体积
目录 一、AABB包围盒二、代码实现三、结果展示四、相关链接本文由CSDN点云侠原创,原文链接。爬虫自重,把自己当个人。 一、AABB包围盒 AABB包围盒又称了 轴对齐包围盒,是点云包围盒里最简单的一种,其计算方法也极其简单。获取包围盒之后,根据包围盒的长宽高进行体积计算即…...

论软件测试工程师 重要性!
在生活中,我们常常会遇到以下几种窘迫时刻: 准备骑共享单车出行,却发现扫码开锁半天,车子都没有反应;手机导航打车,却发现地图定位偏差很大,司机总是跑错地方;买个水,却…...
防御第六次作业-防火墙综合实验(av、url过滤、dns过滤)
目录 拓扑图: 要求: 8 9 10 11 拓扑图 要求 前7个要求在上一篇博客; 8.分公司内部的客户端可以通过域名访问到内部的服务器 9.假设内网用户需要通过外网的web服务器和pop3邮件服务器下载文件和邮件,内网的FTP服务器也需要…...

打码半年,开源一款自定义大屏设计软件!
hi,大家好,我是Tduck马马。 最近我们开源了一款大屏软件-TReport,与大家分享。 TReport是一款基于Vue3技术栈的数据可视化系统,支持静态、动态api等数据源;可用于数据可视化分析、报表分析、海报设计使用。 提供自定…...
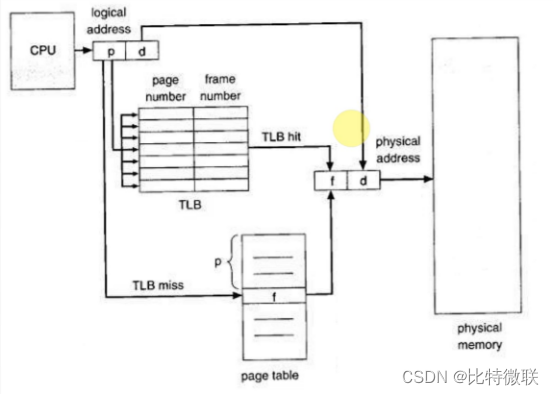
云计算基础-大页内存
大页内存功能概述 什么是大页内存 简单来说,就是通过增大操作系统页的大小来减小页表,从而避免快表缺失 主要应用场景 主要运用于内存密集型业务的虚拟机,比如对于运行数据库系统的虚拟机,采用HugePages(大页)后,可…...
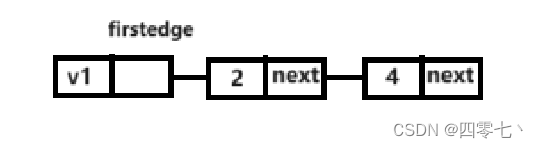
数据结构-邻接链表
介绍 邻接矩阵是运用较多的一种储存图的方法,但如果一张网图边数较少,就会出现二维矩阵中大部分数据为0的情况,浪费储存空间 为了避免空间浪费,也可以采用数组与链表结合的方式来存储图 假设有这样一张图 我们可以先用一个数组…...

十三、集合进阶——单列集合 及 数据结构
单列集合 及 数据结构 13.1 集合体系结构13.1.2 单列集合1. Collection2.Collection 的遍历方式迭代器遍历增强for遍历Lambda表达式遍历 3.List集合List集合的特有方法List集合的遍历方式五种遍历方式对比 4.数据结构1).栈2).队列3)数组4)链表小结5&…...
Android | ArcGIS入门
一、概述 ArcGIS是由Esri开发的地理信息系统(GIS)软件。它用于制图、空间分析和数据可视化。ArcGIS允许用户以各种格式创建、管理、分析和共享地理信息。它通常用于城市规划、环境管理和应急响应等领域。该软件包括一系列工具,用于创建地图、…...
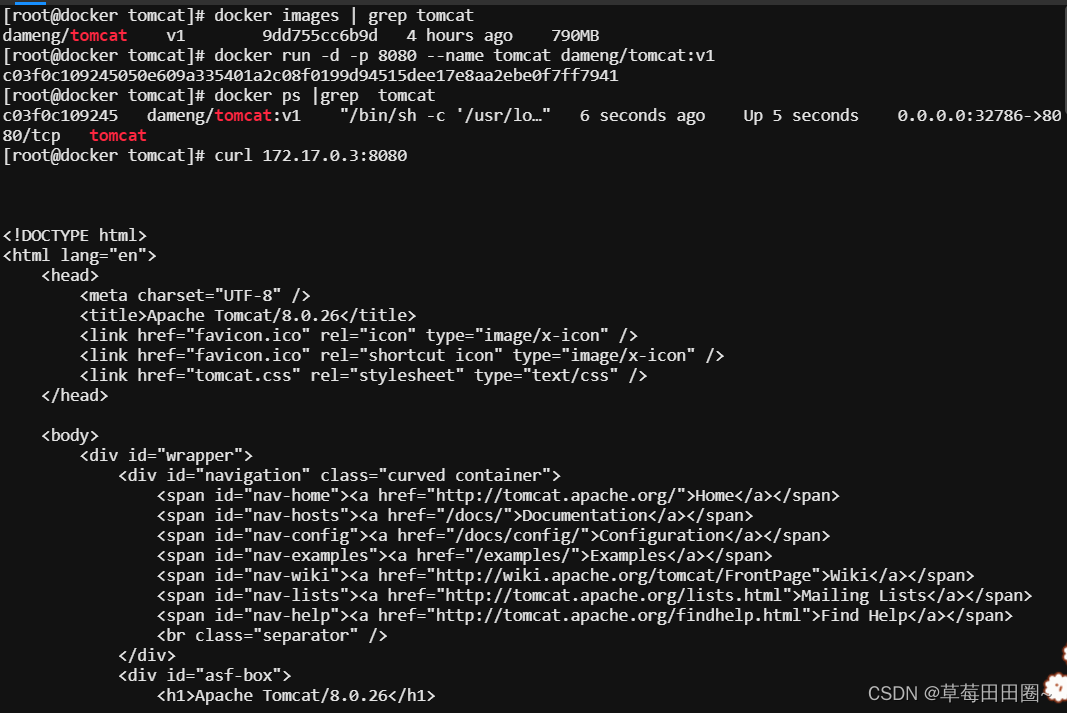
dockerfile文件书写
1.dockerfile构建nginx镜像 1.1书写dockerfile文件 mkdir nginx #创建nginx目录 cd nginx vim dockerfile # 修改文件FROM centos # 基础镜像,默认最新的centos8操作系统 MAINTAINER xianchao # 指定镜像的作者信息 RUN rm -rf /etc/yum.repos.d/* # centos8默认…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...

6.9本日总结
一、英语 复习默写list11list18,订正07年第3篇阅读 二、数学 学习线代第一讲,写15讲课后题 三、408 学习计组第二章,写计组习题 四、总结 明天结束线代第一章和计组第二章 五、明日计划 英语:复习l默写sit12list17&#…...

简约商务通用宣传年终总结12套PPT模版分享
IOS风格企业宣传PPT模版,年终工作总结PPT模版,简约精致扁平化商务通用动画PPT模版,素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...

性能优化中,多面体模型基本原理
1)多面体编译技术是一种基于多面体模型的程序分析和优化技术,它将程序 中的语句实例、访问关系、依赖关系和调度等信息映射到多维空间中的几何对 象,通过对这些几何对象进行几何操作和线性代数计算来进行程序的分析和优 化。 其中࿰…...
