【图论经典题目讲解】CF715B - Complete The Graph
C F 715 B − C o m p l e t e T h e G r a p h \mathrm{CF715B - Complete\ The\ Graph} CF715B−Complete The Graph
D e s c r i p t i o n \mathrm{Description} Description
给定一张 n n n 个点, m m m 条边的无向图,点的编号为 0 ∼ n − 1 0\sim n-1 0∼n−1,对于每条边权为 0 0 0 的边赋一个不超过 1 0 18 10^{18} 1018 的正整数权值,使得 S S S 到 T T T 的最短路长度为 L L L。
S o l u t i o n \mathrm{Solution} Solution
W a y 1 \mathrm{Way\ 1} Way 1
考虑将每 1 1 1 条长度为 0 0 0 的边记录出来,初始将其全部设置为 1 1 1(因为要求边权值 ∈ [ 1 , 1 0 18 ] \in[1,10^{18}] ∈[1,1018]),如果将这些边依次不断地加 1 1 1,则 S S S 到 T T T 的最短路的长度会不断地增加或不变,总之最短路长度是单调不降的。那么,如果有解就必定会找到一种方案,反之则不会。
观察数据范围可知,最多每条边会加到 L L L,有 m m m 条边,那么时间应为 O ( m 2 L log n ) O(m^2L\log n) O(m2Llogn),因为还需加入 Dijkstra 的时间复杂度。
显然,会 TLE。不过,上文已分析最短路的长度是单调不降的,所以满足二分的性质,可以二分总共加 1 1 1 的个数,然后对于每跳边先加 ⌊ 个数 边数 ⌋ \lfloor\frac{个数}{边数}\rfloor ⌊边数个数⌋,之后对于 1 ∼ 个数 m o d 边数 1\sim 个数\bmod 边数 1∼个数mod边数 的边再加 1 1 1 即可。
时间复杂度: O ( m log L log n ) O(m\log L\log n) O(mlogLlogn)
C o d e Code Code
#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int SIZE = 2e4 + 10;int N, M, L, S, T;
int h[SIZE], e[SIZE], ne[SIZE], w[SIZE], idx;
std::vector<int> Id;
int Dist[SIZE], Vis[SIZE];void add(int a, int b, int c)
{e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}int Dijkstra()
{priority_queue<PII, vector<PII>, greater<PII>> Heap;memset(Dist, 0x3f, sizeof Dist);memset(Vis, 0, sizeof Vis);Dist[S] = 0, Heap.push({0, S});while (Heap.size()){auto Tmp = Heap.top();Heap.pop();int u = Tmp.second;if (Vis[u]) continue;Vis[u] = 1;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (Dist[j] > Dist[u] + w[i]){Dist[j] = Dist[u] + w[i];Heap.push({Dist[j], j});}}}return Dist[T];
}int Check(int X)
{for (auto c : Id)w[c] = X / (int)(Id.size() / 2);for (int i = 0; i < (X % (int)(Id.size() / 2)) * 2; i += 2)w[Id[i]] += 1, w[Id[i] ^ 1] += 1;return Dijkstra();
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);memset(h, -1, sizeof h);cin >> N >> M >> L >> S >> T;int u, v, c, Cpy = M;while (M --){cin >> u >> v >> c;if (c) add(u, v, c), add(v, u, c);else{Id.push_back(idx), add(u, v, 1);Id.push_back(idx), add(v, u, 1);}}M = Cpy;if (!Id.size()){if (Dijkstra() == L){cout << "YES" << endl;for (int i = 0; i < idx; i += 2)cout << e[i ^ 1] << " " << e[i] << " " << w[i] << endl;}elsecout << "NO" << endl;return 0;}int l = Id.size() / 2, r = L * M;while (l < r){int mid = l + r >> 1;if (Check(mid) >= L) r = mid;else l = mid + 1;}if (Check(r) != L){cout << "NO" << endl;return 0;}cout << "YES" << endl;for (int i = 0; i < idx; i += 2)cout << e[i ^ 1] << " " << e[i] << " " << w[i] << endl;return 0;
}
W a y 2 \mathrm{Way\ 2} Way 2
从 S S S 开始先做 1 1 1 遍 Dijkstra,记当前 L L L 与 S S S 到 T T T 的最短路的差值为 D i f f Diff Diff(即 D i f f = L − D 1 , T Diff=L-D_{1,T} Diff=L−D1,T)
之后再做第 2 2 2 遍 Dijkstra 的时候,当点 u u u 更新至点 v v v 时且当前边为特殊边(初始变为 0 0 0),若 D 2 , u + w i < D 1 , v + D i f f D_{2,u}+w_i< D_{1,v}+Diff D2,u+wi<D1,v+Diff,则说明这时候最短路长度少了,尽量要让其补上这缺失的部分,即 w i = D 1 , u + D i f f − D 2 , u w_i = D_{1,u}+Diff-D_{2,u} wi=D1,u+Diff−D2,u。修改后,再进行正常 Dijkstra 的更新即可。
注:
D 1 , i D_{1,i} D1,i 表示第 1 1 1 次 Dijkstra 到达 i i i 号点的最短路长度, D 2 , i D_{2,i} D2,i 表示第 2 2 2 次 Dijkstra 到达第 i i i 号点的最短路长度。
C o d e Code Code
#include <bits/stdc++.h>
#define int long longusing namespace std;typedef pair<int, int> PII;
typedef long long LL;const int SIZE = 2e4 + 10;int N, M, L, S, T;
int h[SIZE], e[SIZE], ne[SIZE], w[SIZE], f[SIZE], idx;
int D[2][SIZE], Vis[SIZE];void add(int a, int b, int c)
{if (!c) f[idx] = 1;e[idx] = b, ne[idx] = h[a], w[idx] = max(1ll, c), h[a] = idx ++;
}void Dijkstra(int dist[], int Turn)
{for (int i = 0; i < N; i ++)dist[i] = 1e18, Vis[i] = 0;priority_queue<PII, vector<PII>, greater<PII>> Heap;Heap.push({0, S}), dist[S] = 0;while (Heap.size()){auto Tmp = Heap.top();Heap.pop();int u = Tmp.second;if (Vis[u]) continue;Vis[u] = 1;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (Turn == 2 && f[i] && dist[u] + w[i] < D[0][j] + L - D[0][T])w[i] = w[i ^ 1] = D[0][j] + L - D[0][T] - dist[u];if (dist[j] > dist[u] + w[i]){dist[j] = dist[u] + w[i];Heap.push({dist[j], j});}}}
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);memset(h, -1, sizeof h);cin >> N >> M >> L >> S >> T;int u, v, c;while (M --){cin >> u >> v >> c;add(u, v, c), add(v, u, c);}Dijkstra(D[0], 1);if (L - D[0][T] < 0){cout << "NO" << endl;return 0;}Dijkstra(D[1], 2);if (D[1][T] != L){cout << "NO" << endl;return 0;}cout << "YES" << endl;for (int i = 0; i < idx; i += 2)cout << e[i ^ 1] << " " << e[i] << " " << w[i] << endl;return 0;
}
相关文章:

【图论经典题目讲解】CF715B - Complete The Graph
C F 715 B − C o m p l e t e T h e G r a p h \mathrm{CF715B - Complete\ The\ Graph} CF715B−Complete The Graph D e s c r i p t i o n \mathrm{Description} Description 给定一张 n n n 个点, m m m 条边的无向图,点的编号为 0 ∼ n − 1 0\…...

[office] excel中数据汇总的大全教程文字版 #知识分享#经验分享#知识分享
excel中数据汇总的大全教程文字版 我们在excel中对数据清单上的数据进行分析的一种方法是分类汇总。在“数据”菜单上选择“分类汇总”命令,我们可以在数据清单中插入分类汇总行,然后按照选择的方式对数据进行汇总。同时,在插入分类汇总时&am…...
)
leetcode经典题库(简单)
文章目录 1.两数之和2.反转链表3.合并两个有序列表4.合并两个有序链表5.删除有序数组中的重复项6.从数组中移除元素7. 搜索指定数值在数组中的插入位置8. 数组最后一位加一9. 合并两个有序数组在leetcode上刷了几个和数组相关的简单题,记录在这里。 1.两数之和 给定一个整数…...

python coding with ChatGPT 打卡第21天| 二叉树:最近公共祖先
相关推荐 python coding with ChatGPT 打卡第12天| 二叉树:理论基础 python coding with ChatGPT 打卡第13天| 二叉树的深度优先遍历 python coding with ChatGPT 打卡第14天| 二叉树的广度优先遍历 python coding with ChatGPT 打卡第15天| 二叉树:翻转…...

openGauss学习笔记-224 openGauss性能调优-系统调优-数据库系统参数调优-数据库并发队列参数调优
文章目录 openGauss学习笔记-224 openGauss性能调优-系统调优-数据库系统参数调优-数据库并发队列参数调优224.1 全局并发队列224.2 局部并发队列 openGauss学习笔记-224 openGauss性能调优-系统调优-数据库系统参数调优-数据库并发队列参数调优 数据库提供两种手段进行并发队…...
UE5 C++ 创建可缩放的相机
一.要将相机设置在Pawn类里 1.在MyPawn头文件里,加上摇臂和相机组件 #include "GameFramework/SpringArmComponent.h" #include "Camera/CameraComponent.h" 2.在Pawm里声明SceneComponet,SpringArmComponent,CameraComponent组件…...

Fabric中的溯源方法
背景 在Fabric链码中,我们可以使用PutState方法对一个key的值进行覆盖,当我们再使用GetState查询时是最新的值。如果我们希望找到这个key的修改记录,我们可以使用溯源方法GetHistoryForKey。完整源码链接:https://github.com/hyp…...
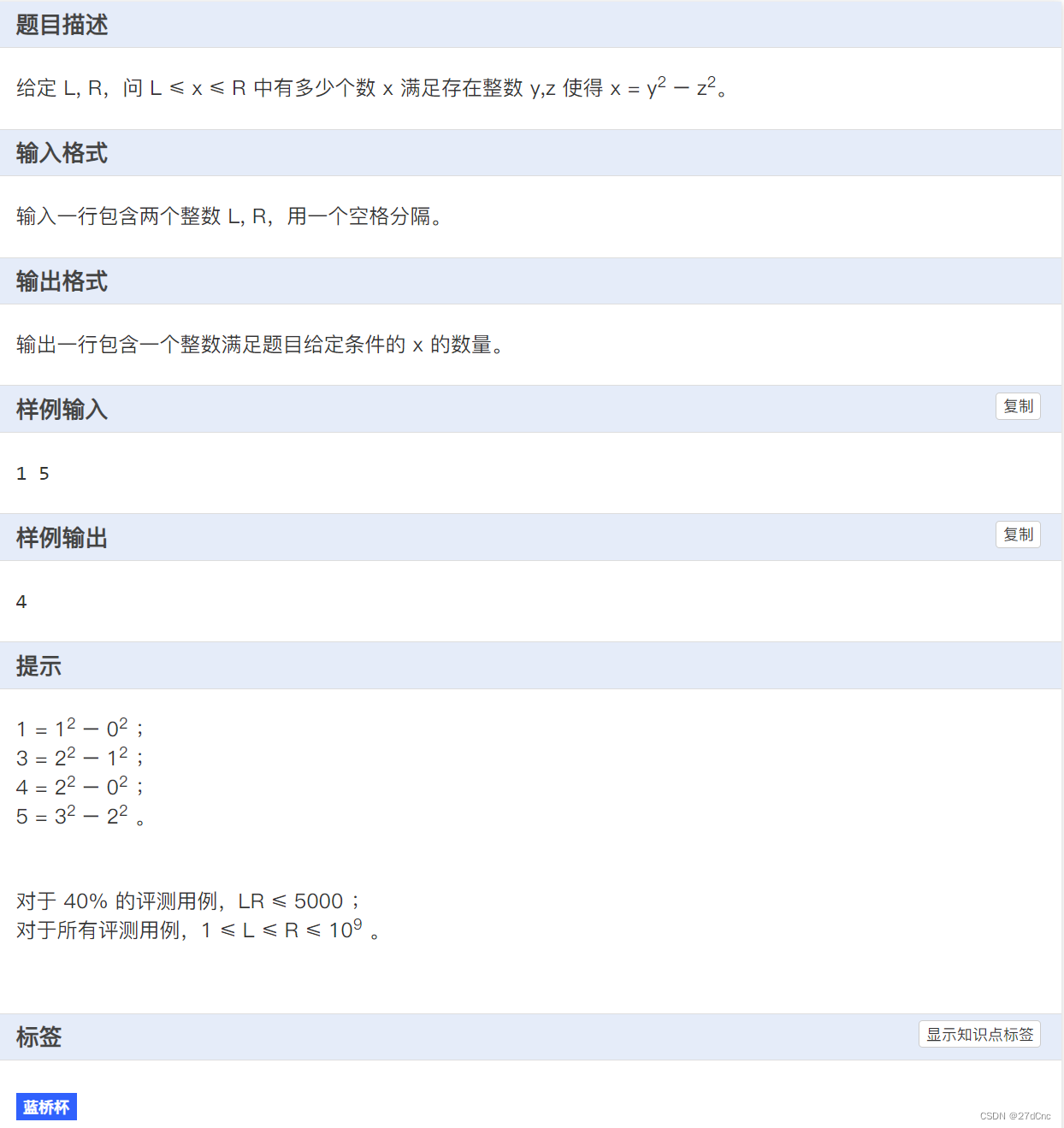
混子文章|蓝桥杯一题 -平方差
题目考点: 平方差 ,平方差奇偶关系 代码 #include<bits/stdc.h> #define Run 0 #define endl "\n" #define N 100005 using unl __int128_t; using ll long long; using namespace std; class Solution { public: void slove() {int sum 0;int L, R; cin &…...

计算机视觉基础:【矩阵】矩阵选取子集
OpenCV的基础是处理图像,而图像的基础是矩阵。 因此,如何使用好矩阵是非常关键的。 下面我们通过一个具体的实例来展示如何通过Python和OpenCV对矩阵进行操作,从而更好地实现对图像的处理。 示例 示例:选取矩阵中指定的行和列的…...

解决laravel-admin安装报错1071 Specified key was too long问题
在执行php artisan admin:install命令安装laravel-admin的时候,如果你使用的数据库是MySQL v5.7.7以下版本就会报下面的错: SQLSTATE[42000]: Syntax error or access violation: 1071 Specified key was too long; max key length is 1000 bytes (SQL:…...

【Python---六大数据结构】
🚀 作者 :“码上有前” 🚀 文章简介 :Python 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 Python---六大数据结构 往期内容前言概述一下可变与不可变 Number四种不同的数值类型Number类型的创建i…...

一个简短的补充------对链表练习题的补充补充
昨天不是写了一篇有关链表的数据结构练习题嘛,其实那篇文章的第二道题还有许多值得我们思考的东西,今天就在这做一个简短的补充。补充一下运用那道题解决另一道题。 给大家看一下绿色让眼睛放松一下。 给定一个链表的头节点 head ,返回链表…...
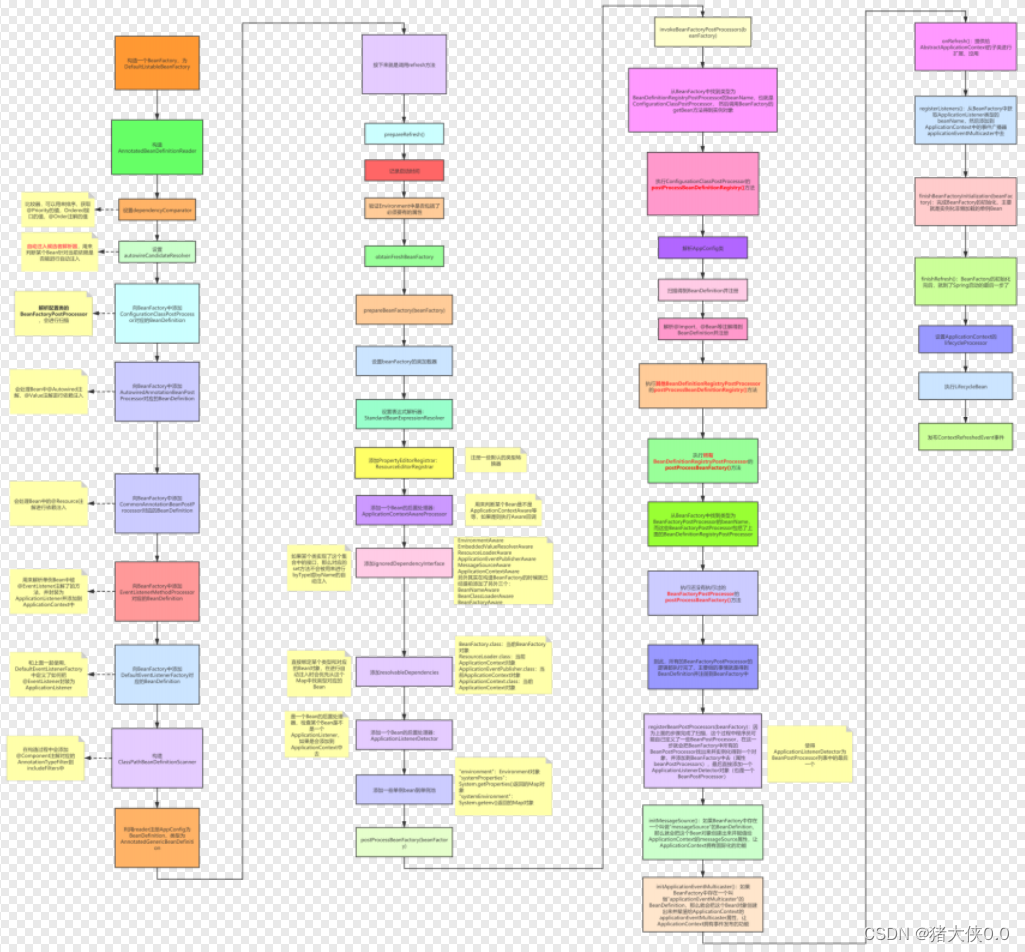
Spring最新核心高频面试题(持续更新)
1 什么是Spring框架 Spring框架是一个开源的Java应用程序开发框架,它提供了很多工具和功能,可以帮助开发者更快地构建企业级应用程序。通过使用Spring框架,开发者可以更加轻松地开发Java应用程序,并且可以更加灵活地组织和管理应…...

[计网底层小探索]:实现并部署多线程并发Tcp服务器框架(基于生产者消费者模型的线程池结构)
文章目录 一.网络层与传输层协议sockaddr结构体继承体系(Linux体系)贯穿计算机系统的网络通信架构图示: 二.实现并部署多线程并发Tcp服务器框架线程池模块序列化反序列化工具模块通信信道建立模块服务器主体模块任务回调模块(根据具体应用场景可重构)Tips:DebugC代码过程中遇到…...

Spring Boot 笔记 020 redis集成
1.1 安装redis Windows 下 Redis 安装与配置 教程_redis windows-CSDN博客 2.1 引入redis坐标 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId></dependency> 2.2 配置…...
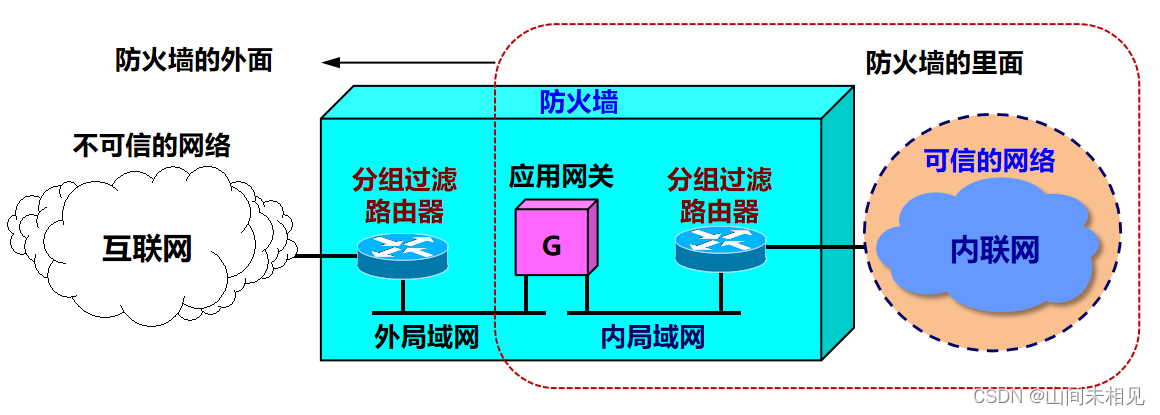
防火墙——计算机网络
前述基于密码的安全机制不能有效解决以下安全问题: 用户入侵: 利用系统漏洞进行未授权登录; 授权用户非法获取更高级别权限等。 软件入侵: 通过网络传播病毒、蠕虫和特洛伊木马。 拒绝服务攻击等。 解决方法: 防火墙&a…...

用html编写的招聘简历
用html编写的招聘简历 相关代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</tit…...

215数组中的第K个最大元素
215数组中的第K个最大元素 题目描述 给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。 请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。 你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。…...

【动态规划】【矩阵快速幂】LeetCode2851. 字符串转换
作者推荐 【深度优先搜索】【树】【有向图】【推荐】685. 冗余连接 II 涉及知识点 【矩阵快速幂】封装类及测试用例及样例 LeetCode 2851. 字符串转换 给你两个长度都为 n 的字符串 s 和 t 。你可以对字符串 s 执行以下操作: 将 s 长度为 l (0 <…...

【LeetCode每日一题】单调栈 402 移掉k位数字
402. 移掉 K 位数字 给你一个以字符串表示的非负整数 num 和一个整数 k ,移除这个数中的 k **位数字,使得剩下的数字最小。请你以字符串形式返回这个最小的数字。 示例 1 : 输入:num "1432219", k 3 输出ÿ…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
