力扣题目训练(17)
2024年2月10日力扣题目训练
- 2024年2月10日力扣题目训练
- 551. 学生出勤记录 I
- 557. 反转字符串中的单词 III
- 559. N 叉树的最大深度
- 241. 为运算表达式设计优先级
- 260. 只出现一次的数字 III
- 126. 单词接龙 II
2024年2月10日力扣题目训练
2024年2月10日第十七天编程训练,今天主要是进行一些题训练,包括简单题3道、中等题2道和困难题1道。惰性太强现在才完成,不过之后我会认真完成的。
551. 学生出勤记录 I
链接: 出勤记录
难度: 简单
题目:

运行示例:

思路:
这道题就是一个简单的遍历,只需在遍历时判断是否不符合条件的情况即可。
代码:
class Solution {
public:bool checkRecord(string s) {int re1 = 0;int re2 = 0;for(int i = 0; i < s.size(); i++){if(s[i] == 'A'){re1++;re2 = 0;if(re1 == 2) return false;}else if(s[i] == 'L'){re2++;if(re2 == 3) return false;}else{re2 = 0;}}return true;}
};557. 反转字符串中的单词 III
链接: 反转字符串中的单词
难度: 简单
题目:

运行示例:

思路:
这道题主要是遍历找到空格,根据空格将单词进行反转。
代码:
class Solution {
public:string reverseWords(string s) {int left = 0;string ans;for(int i = 0; i < s.size(); i++){if(s[i] == ' '){string tmp = s.substr(left,i-left);cout<<"asdf:"<<tmp<<endl;reverse(tmp.begin(),tmp.end());ans += tmp;ans += ' ';left = i+1;}}if(left != s.size()){string tmp = s.substr(left,s.size()-left);reverse(tmp.begin(),tmp.end());ans += tmp;}return ans;}
};
559. N 叉树的最大深度
链接: N 叉树的最大深度
难度: 简单
题目:

运行示例:
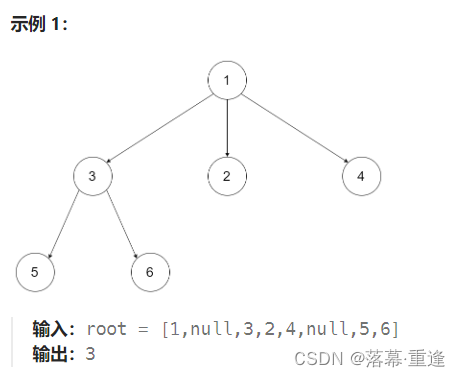
思路:
这道题求N叉树的深度,与543. 二叉树的直径类似,只是从二叉树拓展到N叉树而已。大家也可以先写一下104. 二叉树的最大深度添加链接描述和543. 二叉树的直径进行锻炼之后再写这道题。
代码:
class Solution {
public:int maxDepth(Node* root) {if(root == NULL) return 0;int maxChildDepth = 0;vector<Node*> children = root->children;for(int i = 0; i < children.size(); i++){int childrenDepth = maxDepth(children[i]);maxChildDepth = max(maxChildDepth,childrenDepth);}return maxChildDepth+1;}
};
241. 为运算表达式设计优先级
链接: 优先级
难度: 中等
题目:

运行示例:

思路:
这道题核心就是分治,利用运算符进行分割,递归求解结果。遍历字符串,每次遇到运算符时,将字符串分为运算符左侧和运算符右侧两部分,递归求解这两部分的结果。此外为避免重复计算我们可以利用一个哈希表记录已经计算过的部分。
代码:
class Solution {
public:unordered_map<string,vector<int>> memo;vector<int> findsome(string s){if(memo.find(s) != memo.end()) return memo[s];vector<int> ans;for(int i = 0; i <s.size(); i++){if(!isdigit(s[i])){vector<int> ans1 = findsome(s.substr(0,i));vector<int> ans2 = findsome(s.substr(i+1));if(s[i] == '+'){for(auto& x: ans1)for(auto& y: ans2) ans.push_back(x+y);}else if(s[i] == '-')for(auto& x: ans1)for(auto& y: ans2) ans.push_back(x - y);elsefor(auto& x: ans1)for(auto& y: ans2) ans.push_back(x * y);}}if(ans.empty()) ans.push_back(stoi(s));memo[s] = ans;return ans;}vector<int> diffWaysToCompute(string expression) {return findsome(expression);}
};
260. 只出现一次的数字 III
链接: 只出现一次的数字
难度: 中等
题目:
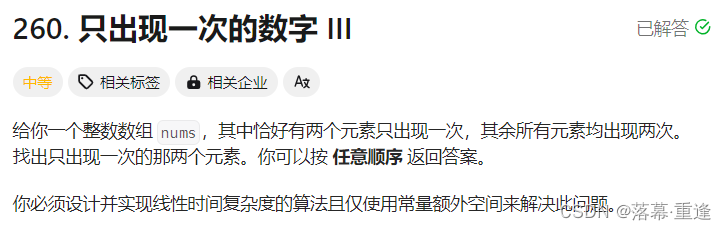
运行示例:

思路:
这道题考虑位运算,我们知道异或运算有以下性质:
任何数和 0做异或运算,结果仍然是原来的数,即 x⊕0=x;
任何数和其自身做异或运算,结果是 0,即 x⊕x=0;
根据这条性质,我们将数组中的所有数字进行异或运算,得到的结果即为两个只出现一次的数字的异或结果。但由于这两个数字不相等,因此异或结果中至少存在一位为 1。我们可以通过 lowbit 运算找到异或结果中最低位的 1,并将数组中的所有数字按照该位是否为 1分为两组,这样两个只出现一次的数字就被分到了不同的组中。 从而得到结果。
代码:
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {long long sum = 0;for(auto& num:nums) sum ^= num;int lsb = sum &(-sum);int a = 0,b = 0;for (auto& num: nums) {if (num & lsb) {a ^= num;}else {b ^= num;}}return {a,b};}
};
126. 单词接龙 II
链接: 单词接龙
难度: 困难
题目:

运行示例:

思路:
这道题我知道是应该用递归和回溯,但是不知道如何动笔。官方是利用广度优先搜索 + 回溯,建立图。
本题要求的是最短转换序列,看到最短首先想到的就是广度优先搜索。但是本题没有给出显示的图结构,根据单词转换规则:把每个单词都抽象为一个顶点,如果两个单词可以只改变一个字母进行转换,那么说明它们之间有一条双向边。因此我们只需要把满足转换条件的点相连,就形成了一张图。根据示例 1 中的输入,我们可以建出下图:
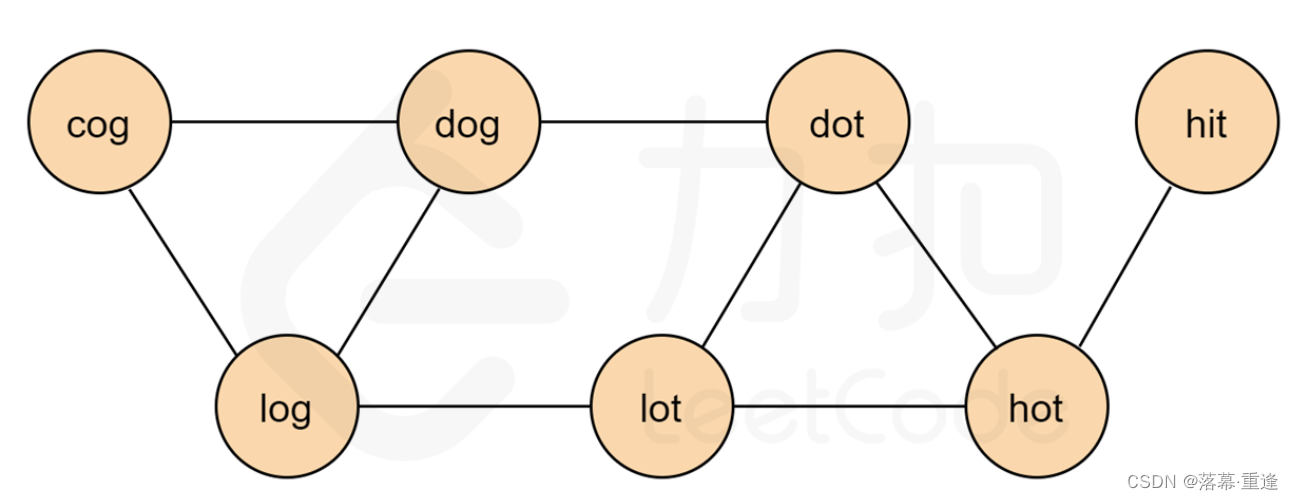
基于该图,我们以 “hit"为图的起点, 以 “cog"为终点进行广度优先搜索,寻找 “hit"到 “cog"的最短路径。下图即为答案中的一条路径。
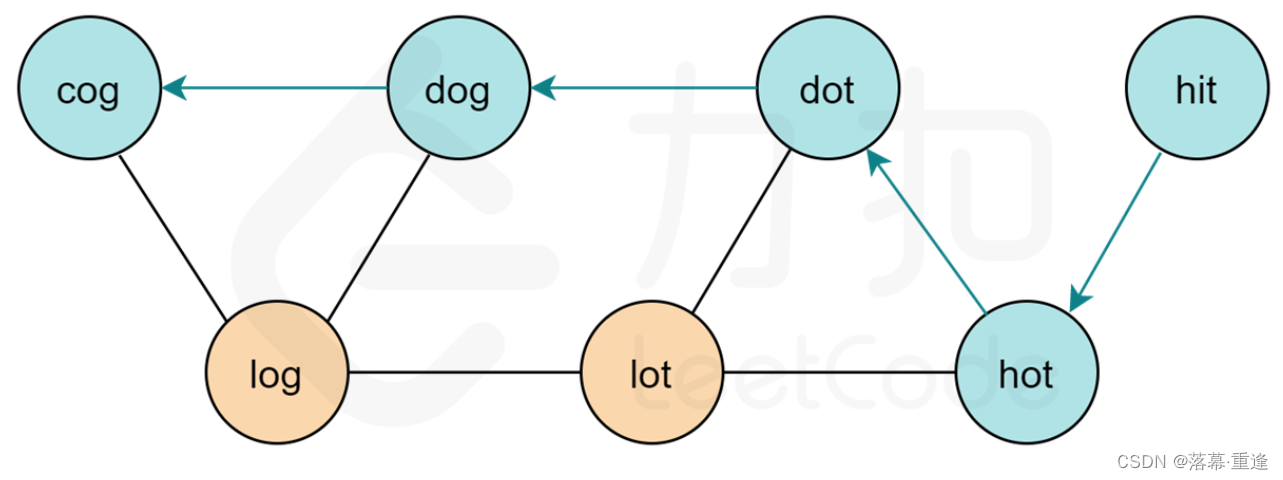
由于要求输出所有的最短路径,因此我们需要记录遍历路径,然后通过回溯得到所有的最短路径。
细节
- 从一个单词出发,修改每一位字符,将它修改成为 ‘a’到 ‘z’中的所有字符,看看修改以后是不是在题目中给出的单词列表中;
- 有一些边的关系,由于不是最短路径上的边,不可以被记录下来。为此,我们为扩展出的单词记录附加的属性:层数。即下面代码中的steps。如果当前的单词扩散出去得到的单词的层数在以前出现过,则不应该记录这样的边的关系。
代码:
class Solution {
public:vector<vector<string>> findLadders(string beginWord, string endWord, vector<string> &wordList) {vector<vector<string>> res;// 因为需要快速判断扩展出的单词是否在 wordList 里,因此需要将 wordList 存入哈希表,这里命名为「字典」unordered_set<string> dict = {wordList.begin(), wordList.end()};// 修改以后看一下,如果根本就不在 dict 里面,跳过if (dict.find(endWord) == dict.end()) {return res;}// 特殊用例处理dict.erase(beginWord);// 第 1 步:广度优先搜索建图// 记录扩展出的单词是在第几次扩展的时候得到的,key:单词,value:在广度优先搜索的第几层unordered_map<string, int> steps = {{beginWord, 0}};// 记录了单词是从哪些单词扩展而来,key:单词,value:单词列表,这些单词可以变换到 key ,它们是一对多关系unordered_map<string, set<string>> from = {{beginWord, {}}};int step = 0;bool found = false;queue<string> q = queue<string>{{beginWord}};int wordLen = beginWord.length();while (!q.empty()) {step++;int size = q.size();for (int i = 0; i < size; i++) {const string currWord = move(q.front());string nextWord = currWord;q.pop();// 将每一位替换成 26 个小写英文字母for (int j = 0; j < wordLen; ++j) {const char origin = nextWord[j];for (char c = 'a'; c <= 'z'; ++c) {nextWord[j] = c;if (steps[nextWord] == step) {from[nextWord].insert(currWord);}if (dict.find(nextWord) == dict.end()) {continue;}// 如果从一个单词扩展出来的单词以前遍历过,距离一定更远,为了避免搜索到已经遍历到,且距离更远的单词,需要将它从 dict 中删除dict.erase(nextWord);// 这一层扩展出的单词进入队列q.push(nextWord);// 记录 nextWord 从 currWord 而来from[nextWord].insert(currWord);// 记录 nextWord 的 stepsteps[nextWord] = step;if (nextWord == endWord) {found = true;}}nextWord[j] = origin;}}if (found) {break;}}// 第 2 步:回溯找到所有解,从 endWord 恢复到 beginWord ,所以每次尝试操作 path 列表的头部if (found) {vector<string> Path = {endWord};backtrack(res, endWord, from, Path);}return res;}void backtrack(vector<vector<string>> &res, const string &Node, unordered_map<string, set<string>> &from,vector<string> &path) {if (from[Node].empty()) {res.push_back({path.rbegin(), path.rend()});return;}for (const string &Parent: from[Node]) {path.push_back(Parent);backtrack(res, Parent, from, path);path.pop_back();}}
};相关文章:

力扣题目训练(17)
2024年2月10日力扣题目训练 2024年2月10日力扣题目训练551. 学生出勤记录 I557. 反转字符串中的单词 III559. N 叉树的最大深度241. 为运算表达式设计优先级260. 只出现一次的数字 III126. 单词接龙 II 2024年2月10日力扣题目训练 2024年2月10日第十七天编程训练,今…...

【react】react中和vue中的provide/inject、context写法示例
react写法 在 React 中,provide和inject的功能类似于 Vue.js 中的 provide和inject。它们都是用于跨组件层次传递数据的。 在 React 中,没有内置的 provide 和 inject 函数。但是,你可以使用 React 的 Context 来实现类似的功能。 Context…...
)
MySQL 的存储引擎(基本介绍)
文章目录 前言MySQL 的存储引擎介绍存储引擎是什么?存储引擎的特性? Innodb 与 Mylsam 的区别行级锁与表级锁是否支持事务是否支持恢复数据是否支持外键是否支持 MVCC 总结 前言 好文章不要错过,前两天跟大家分享的文章 1.MySQL的基础架构 2.SQL语句的…...

Unity3D 实现基于物理引擎的绳子关节解析详解
前言 在游戏开发中,有时候我们需要实现绳子关节效果,比如在射击游戏中射击绳子,或者在平衡游戏中使用绳子作为支撑。本文将详细介绍如何使用Unity3D的物理引擎实现绳子关节效果。 对惹,这里有一个游戏开发交流小组,希…...
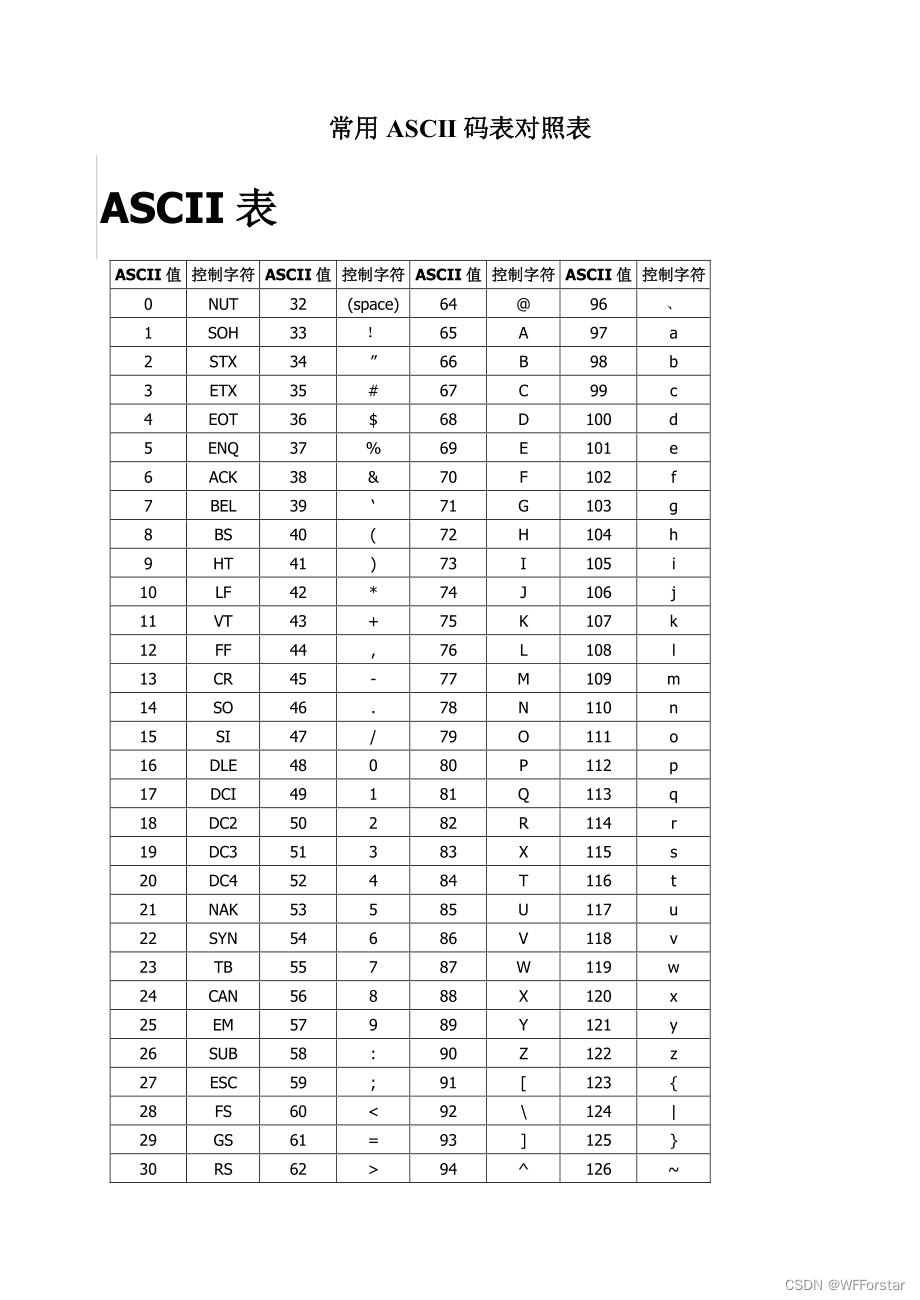
C语言二级易忘易错易混知识点(自用)
1.数组名不能自加。 因为数组名实际上是一个指针,指向数组的第一个元素的地址。数组名在编译器中被视为常量,它的值是固定的,不能改变。 要访问数组的不同元素,应该使用数组名加上偏移量的方式来访问。 2.共用体只有最后一次赋值…...

js_三种方法实现深拷贝
深拷贝( 递归 ) 适用于需要完全独立于原始对象的场景,特别是当对象内部有引用类型时,为了避免修改拷贝后的对象影响到原始对象,就需要使用深拷贝。 // 原始对象 const obj { uname: Lily,age: 19,hobby: [乒乓球, 篮球…...

【图论经典题目讲解】CF715B - Complete The Graph
C F 715 B − C o m p l e t e T h e G r a p h \mathrm{CF715B - Complete\ The\ Graph} CF715B−Complete The Graph D e s c r i p t i o n \mathrm{Description} Description 给定一张 n n n 个点, m m m 条边的无向图,点的编号为 0 ∼ n − 1 0\…...

[office] excel中数据汇总的大全教程文字版 #知识分享#经验分享#知识分享
excel中数据汇总的大全教程文字版 我们在excel中对数据清单上的数据进行分析的一种方法是分类汇总。在“数据”菜单上选择“分类汇总”命令,我们可以在数据清单中插入分类汇总行,然后按照选择的方式对数据进行汇总。同时,在插入分类汇总时&am…...
)
leetcode经典题库(简单)
文章目录 1.两数之和2.反转链表3.合并两个有序列表4.合并两个有序链表5.删除有序数组中的重复项6.从数组中移除元素7. 搜索指定数值在数组中的插入位置8. 数组最后一位加一9. 合并两个有序数组在leetcode上刷了几个和数组相关的简单题,记录在这里。 1.两数之和 给定一个整数…...

python coding with ChatGPT 打卡第21天| 二叉树:最近公共祖先
相关推荐 python coding with ChatGPT 打卡第12天| 二叉树:理论基础 python coding with ChatGPT 打卡第13天| 二叉树的深度优先遍历 python coding with ChatGPT 打卡第14天| 二叉树的广度优先遍历 python coding with ChatGPT 打卡第15天| 二叉树:翻转…...

openGauss学习笔记-224 openGauss性能调优-系统调优-数据库系统参数调优-数据库并发队列参数调优
文章目录 openGauss学习笔记-224 openGauss性能调优-系统调优-数据库系统参数调优-数据库并发队列参数调优224.1 全局并发队列224.2 局部并发队列 openGauss学习笔记-224 openGauss性能调优-系统调优-数据库系统参数调优-数据库并发队列参数调优 数据库提供两种手段进行并发队…...
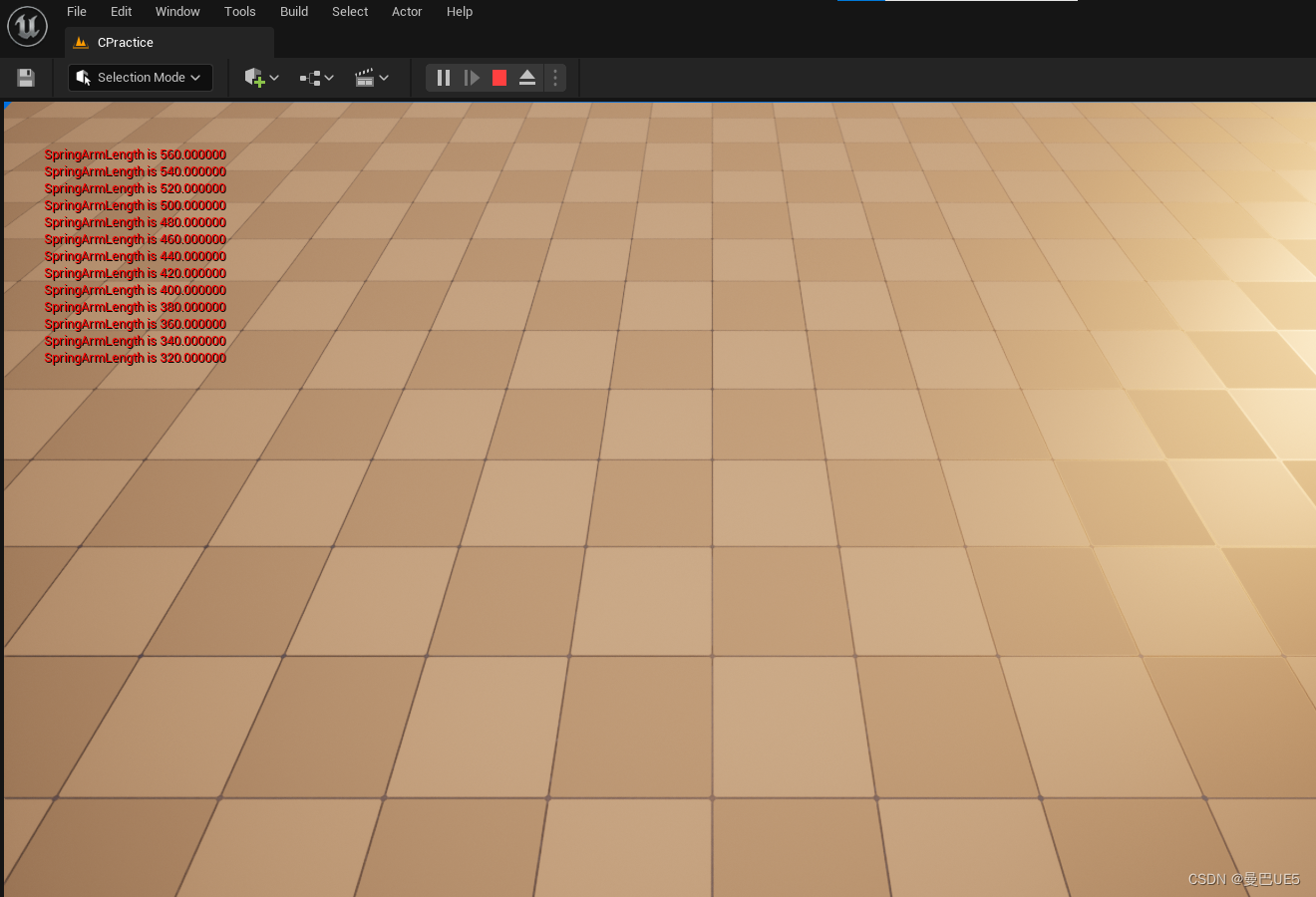
UE5 C++ 创建可缩放的相机
一.要将相机设置在Pawn类里 1.在MyPawn头文件里,加上摇臂和相机组件 #include "GameFramework/SpringArmComponent.h" #include "Camera/CameraComponent.h" 2.在Pawm里声明SceneComponet,SpringArmComponent,CameraComponent组件…...

Fabric中的溯源方法
背景 在Fabric链码中,我们可以使用PutState方法对一个key的值进行覆盖,当我们再使用GetState查询时是最新的值。如果我们希望找到这个key的修改记录,我们可以使用溯源方法GetHistoryForKey。完整源码链接:https://github.com/hyp…...
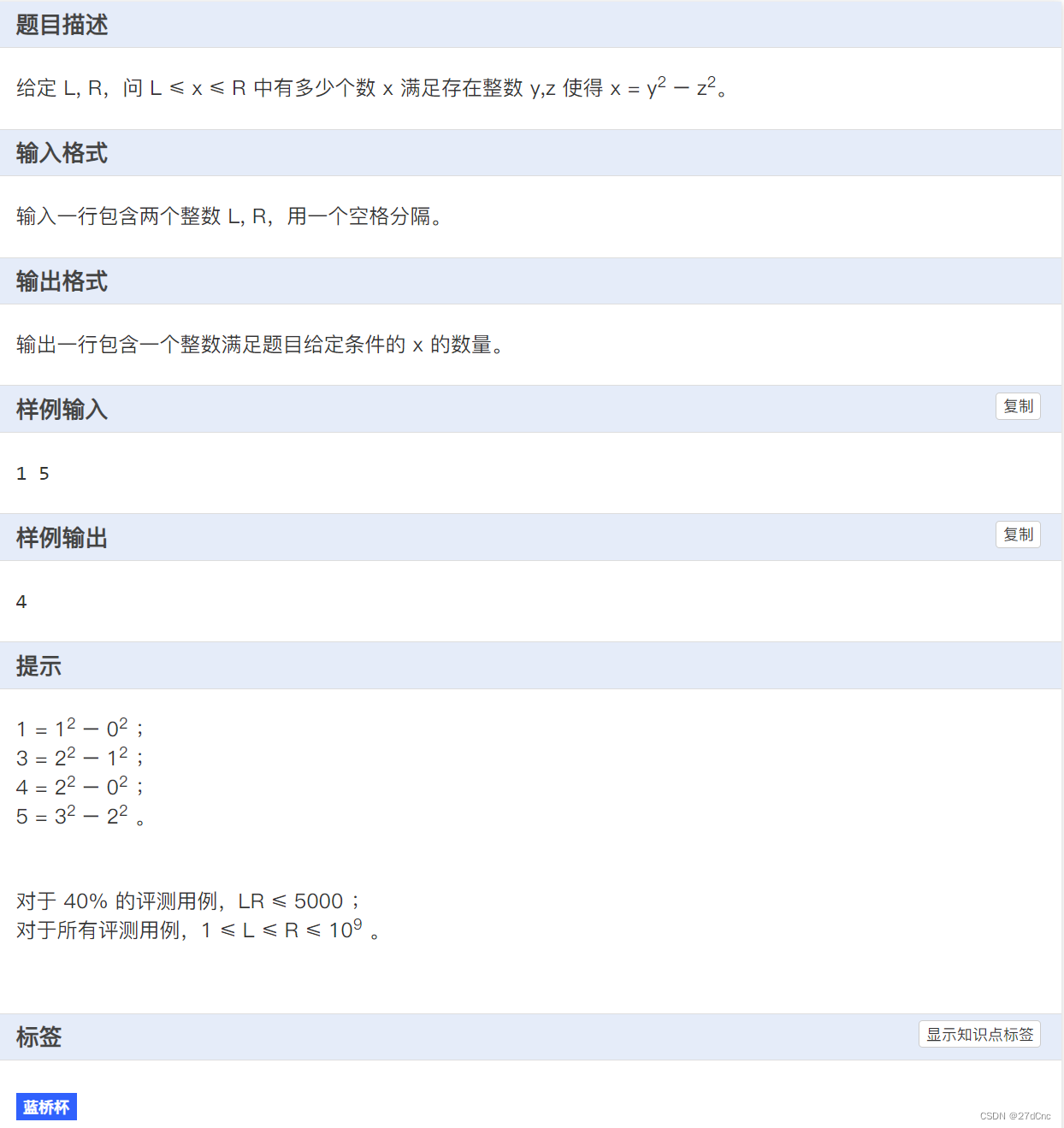
混子文章|蓝桥杯一题 -平方差
题目考点: 平方差 ,平方差奇偶关系 代码 #include<bits/stdc.h> #define Run 0 #define endl "\n" #define N 100005 using unl __int128_t; using ll long long; using namespace std; class Solution { public: void slove() {int sum 0;int L, R; cin &…...

计算机视觉基础:【矩阵】矩阵选取子集
OpenCV的基础是处理图像,而图像的基础是矩阵。 因此,如何使用好矩阵是非常关键的。 下面我们通过一个具体的实例来展示如何通过Python和OpenCV对矩阵进行操作,从而更好地实现对图像的处理。 示例 示例:选取矩阵中指定的行和列的…...

解决laravel-admin安装报错1071 Specified key was too long问题
在执行php artisan admin:install命令安装laravel-admin的时候,如果你使用的数据库是MySQL v5.7.7以下版本就会报下面的错: SQLSTATE[42000]: Syntax error or access violation: 1071 Specified key was too long; max key length is 1000 bytes (SQL:…...

【Python---六大数据结构】
🚀 作者 :“码上有前” 🚀 文章简介 :Python 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 Python---六大数据结构 往期内容前言概述一下可变与不可变 Number四种不同的数值类型Number类型的创建i…...

一个简短的补充------对链表练习题的补充补充
昨天不是写了一篇有关链表的数据结构练习题嘛,其实那篇文章的第二道题还有许多值得我们思考的东西,今天就在这做一个简短的补充。补充一下运用那道题解决另一道题。 给大家看一下绿色让眼睛放松一下。 给定一个链表的头节点 head ,返回链表…...
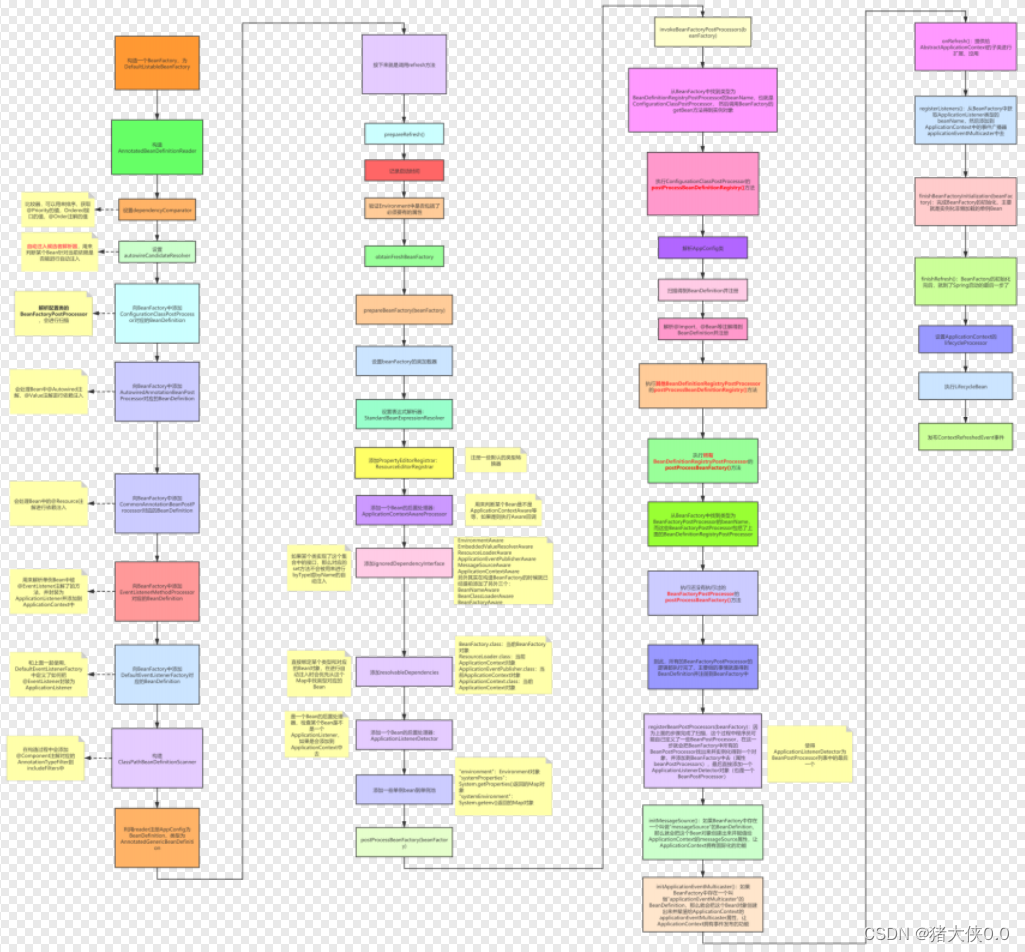
Spring最新核心高频面试题(持续更新)
1 什么是Spring框架 Spring框架是一个开源的Java应用程序开发框架,它提供了很多工具和功能,可以帮助开发者更快地构建企业级应用程序。通过使用Spring框架,开发者可以更加轻松地开发Java应用程序,并且可以更加灵活地组织和管理应…...

[计网底层小探索]:实现并部署多线程并发Tcp服务器框架(基于生产者消费者模型的线程池结构)
文章目录 一.网络层与传输层协议sockaddr结构体继承体系(Linux体系)贯穿计算机系统的网络通信架构图示: 二.实现并部署多线程并发Tcp服务器框架线程池模块序列化反序列化工具模块通信信道建立模块服务器主体模块任务回调模块(根据具体应用场景可重构)Tips:DebugC代码过程中遇到…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
