C#,数值计算,矩阵的乔莱斯基分解(Cholesky decomposition)算法与源代码

一、安德烈·路易斯·乔尔斯基
安德烈·路易斯·乔尔斯基出生于法国波尔多以北的查伦特斯海域的蒙古扬。他在波尔多参加了Lycée e,并于1892年11月14日获得学士学位的第一部分,于1893年7月24日获得第二部分。1895年10月15日,乔尔斯基进入莱科尔理工学院,在当年223名入学学生中排名第88位。他在莱科尔理工学院的教授包括卡米尔·乔丹和发现放射性的著名物理学家亨利·贝克勒尔。在成功的两年后,他于1897年参加了莱科尔理工学院的期末考试。在222名学生中,他提高了自己的地位,在这些考试中排名第38位。随后,他加入军队,成为少尉,并从1897年10月开始在炮兵学校学习。他在1899年完成了学业,并保持了稳步的进步,因为现在他在那一年获得资格的86名学生中排名第五。
突尼斯当时仍然是奥斯曼帝国的正式一部分,但在1883年突尼斯和法国政府签署的《马尔萨公约》之后,它一直是法国的保护国。法国人稳定了经济,建立了现代通讯。从1902年1月到6月,乔尔斯基在突尼斯执行了一项任务,然后从1902年11月到1903年5月,他被派去执行第二项任务。1903年12月31日,乔尔斯基开始在阿尔及利亚服役。那个国家从法国得到的待遇比突尼斯少得多。法国人建立了对该国及其原住民的统治,但发展了新的通讯、医院和医疗服务。他于1904年6月6日离开阿尔及利亚。
乔尔斯基职业生涯中最重要的一步是他于1905年6月进入陆军地理服务部测地部门,据报道他在那里:-
... 他有敏锐的智力和出色的数学能力,有探究精神和独创性的想法。
德拉姆布雷在1798年春天完成了基线测量,这是他对定义米的贡献的一部分。1882年,法国专家回到了德拉姆布雷的基线,但没有重新测量它,而是倾向于通过三角测量间接检查德拉姆布雷的计算。20世纪第一个十年,巴黎子午线修订后,计划对法国进行新的三角测量。调整网格的问题让地理服务部门的官员非常担忧,他们迫切希望找到一种简单、快速、准确的方法。为了用最小二乘法求解条件方程,Cholesky发明了一个非常巧妙的计算程序,该程序立即被证明非常有用:它现在被称为Cholesky方法,我们将在下面描述它。1905年9月26日,他成为中尉,两年后于1907年5月10日结婚。乔尔斯基和他的妻子有三个孩子;一个儿子和两个女儿。
克里特岛是奥斯曼帝国的一部分已经有200年了,但随着帝国的衰落,欧洲的主要国家打算参与克里特岛的未来。1896年,克里特岛发生了一场反对土耳其人的革命,之后希腊试图取得控制权,列强强行达成了和解。法国人负责西蒂亚区,意大利人负责伊拉佩特拉区,英国人负责伊拉克利安区,俄罗斯人负责雷瑟姆农区,而四人共同负责查尼亚区。法国军队在克里特岛的司令部鲁班斯基上校曾是测地学家,希望在岛上进行测绘工作。1906年3月和4月,测地科长布尔乔亚中校进行了初步侦察。乔尔斯基于1907年11月7日被派往克里特岛,作为执行任务的三名军官之一。他在卡沃西平原测量了基线,并使用天文测量来确定基线南端的精确位置。在他的同事被派去执行其他任务后,乔尔斯基进行了三角测量,并对法国和英国的区域进行了地形测量。他在极其困难的条件下成功地进行了三角测量,因为克里特岛冬季高山上降雪量很大。然而,政治事件阻止了土地调查的进行,乔莱斯基于1908年6月25日离开克里特岛。
1909年3月25日,他被任命为第二步兵团团长,并于1909年9月至1911年9月随部队执行任务。1911年晚些时候,他回到了陆军地理服务局的测地部门,并被分配到阿尔及利亚和突尼斯工作,七年前他已经在那里积累了经验。从1911年10月27日至1912年4月24日,再从1912年10月23日至1913年4月17日,他在阿尔及利亚和突尼斯进行了精密水准测量工作。这项工作旨在为修建铁路线做准备。突尼斯的电网建设于1913-1914年冬季完成,之后有一段时间进行检查和调整。在摩洛哥也必须进行类似的工作,Cholesky设计了一些方法,使工作能够更快地进行,但仍然保持必要的准确性。在测试了他的程序后,这些程序于1912年7月开始在摩洛哥使用,工作于1913年1月完成。
1913年5月25日,乔莱斯基被分配到外交部,并被任命为突尼斯摄政区地形局局长。他开始在那里工作,但在1914年秋天第一次世界大战爆发后,他被调到其他地方工作。1915年1月,他开始组织火炮射击,2月被派往沃斯的一个部队工作。1916年9月,他被派往罗马尼亚执行军事任务,在那里担任罗马尼亚军队地理服务处处长。他于1917年7月晋升,并继续在罗马尼亚服役至1918年2月。
乔莱斯基于1918年8月31日凌晨5点在法国北部的战场上受伤身亡。在他死后,他的一位同事,贝诺伊特司令,在《自然推断法中线性方程组解析法的起源》一书中发表了乔尔斯基的计算方法,以解决一些最小二乘数据拟合问题。应用méthodeála resolution d'un Systemème Definition d'quations lineaires(首席检察官Cholesky)Ⓣ, 发表于1924年的公报géodesique。
Cholesky分解(或Cholesky分解)采用对称正定矩阵AA,并将其写成a=LL'a=LL′
其中,LL是一个下三角矩阵,具有正对角项(有时称为Cholesky三角形),L'L′
是LL的转置。要解Ax=bsolveAx=b,现在需要解LL'x=bLL′
x=b所以把y=L'xy=L′
x表示Ly=bLy=b,解为yy,然后y=L'xy=L′
对x进行求解,得到解。该方法的优点在于,当MM是三角形矩阵时,求解Mx=bMx=b型方程非常简单。
该方法在1924年出版后很少受到关注,但杰克·托德在二战期间将其纳入了伦敦国王学院的分析课程。1948年,福克斯、赫斯基和威尔金森在一篇论文中对该方法进行了分析,而图灵在同一年发表了一篇关于该方法稳定性的论文。
二、乔尔斯基分解(Cholesky decomposition)
矩阵分解 (decomposition, factorization)是将矩阵拆解为数个矩阵的乘积,可分为三角分解、满秩分解、QR分解、Jordan分解和SVD(奇异值)分解等,常见的有三种:
(1)三角分解法 (Triangular Factorization)
(2)QR 分解法 (QR Factorization)
(3)奇异值分解法 (SVD,Singular Value Decomposition)

三角分解法亦称因子分解法,由消元法演变而来的解线性方程组的一类方法。设方程组的矩阵形式为Ax=b,三角分解法就是将系数矩阵A分解为一个下三角矩阵L和一个上三角矩阵U之积:A=LU,然后依次解两个三角形方程组Ly=b和Ux=y,而得到原方程组的解,例如,杜利特尔分解法、乔莱斯基分解法等就是三角分解法。
乔莱斯基分解法(Cholesky decomposition method),亦称平方根法,属于三角分解法之一。
楚列斯基分解(Cholesky decomposition)是1993年公布的数学名词。
乔莱斯基、乔里斯基分解,同。
using System;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{/// <summary>/// 乔莱斯基分解/// </summary>public static partial class Algorithm_Gallery{public static int[,] Cholesky_Decomposition(int[,] matrix){int n = matrix.GetLength(0);int[,] lower = new int[n, n];for (int i = 0; i < n; i++){for (int j = 0; j <= i; j++){int sum = 0;if (j == i){for (int k = 0; k < j; k++){sum += (int)Math.Pow(lower[j, k], 2);}lower[j, j] = (int)Math.Sqrt(matrix[j, j] - sum);}else{for (int k = 0; k < j; k++){sum += (lower[i, k] * lower[j, k]);}lower[i, j] = (matrix[i, j] - sum) / lower[j, j];}}}return lower;}}
}
相关文章:

C#,数值计算,矩阵的乔莱斯基分解(Cholesky decomposition)算法与源代码
一、安德烈路易斯乔尔斯基 安德烈路易斯乔尔斯基出生于法国波尔多以北的查伦特斯海域的蒙古扬。他在波尔多参加了Lyce e,并于1892年11月14日获得学士学位的第一部分,于1893年7月24日获得第二部分。1895年10月15日,乔尔斯基进入莱科尔理工学院…...

docker 备份 mysql
使用 Docker 执行 MySQL 备份是一个实用的操作,可以帮助你确保数据的安全性和可恢复性。这里有一步步的指导帮你完成: 1. 确定 MySQL 容器名称或 ID 首先,你需要知道运行 MySQL 数据库的容器的名称或 ID。可以通过下面的命令查看所有正在运…...
使用C# Net6连接国产达梦数据库记录
达梦官网:http://www.dameng.com/ 1 下载达梦并进行安装 下载地址:官网首页——服务与合作——下载中心(https://www.dameng.com/list_103.html) 根据需要自行下载需要的版本,测试版本为:x86 win64 DM8版…...
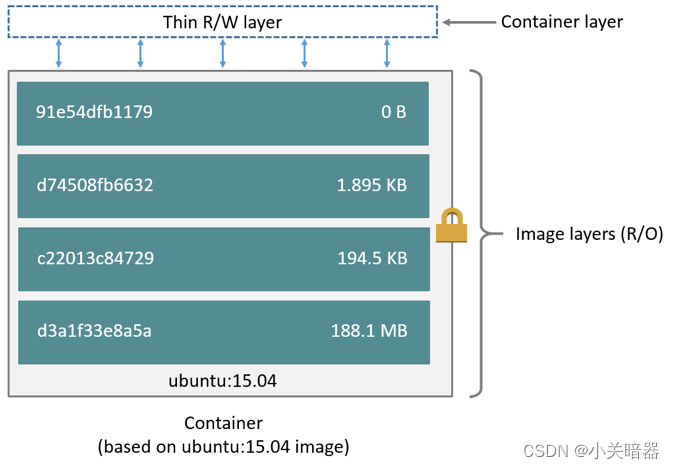
docker (八)-dockerfile制作镜像
一 dockerfile dockerfile通常包含以下几个常用命令: FROM ubuntu:18.04 WORKDIR /app COPY . . RUN make . CMD python app.py EXPOSE 80 FROM 打包使用的基础镜像WORKDIR 相当于cd命令,进入工作目录COPY 将宿主机的文件复制到容器内RUN 打包时执…...
springcloud-网关(gateway)
springcloud-网关(gateway) 概述 \Spring Cloud Gateway旨在提供一种简单而有效的方式来路由到API,并为其提供跨领域的关注,如:安全、监控/指标和容错 常用术语 Route(路由): 网关的基本构件。它由一个ID、一个目的地…...
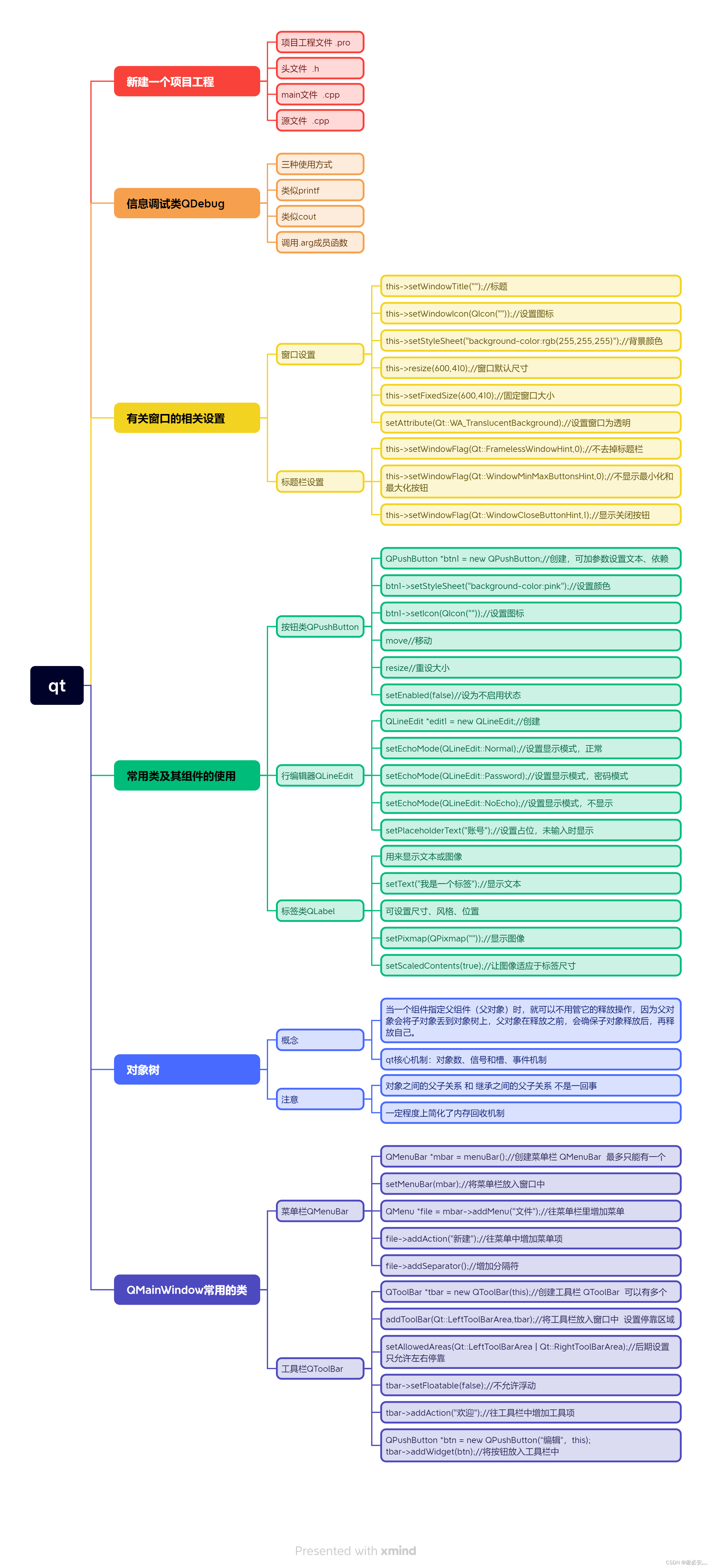
2.20 day2 QT
自由发挥登录窗口的应用场景,实现一个登录窗口界面 #include "widget.h"Widget::Widget(QWidget *parent): QWidget(parent) {//窗口相关设置this->setWindowTitle("登入页面"); //设置 窗口 标题this->setWindowIcon(QIcon("D:…...
【C++语法基础】4.分支和循环结构(✨新手推荐阅读)
前言 在C编程中,分支和循环结构是控制程序流程的基本工具。分支结构允许程序根据特定条件执行不同的代码块,而循环结构则允许程序重复执行某个代码块。 分支结构 if 语句 if 语句是最基本的分支结构,它根据条件的真假来决定是否执行某段代…...
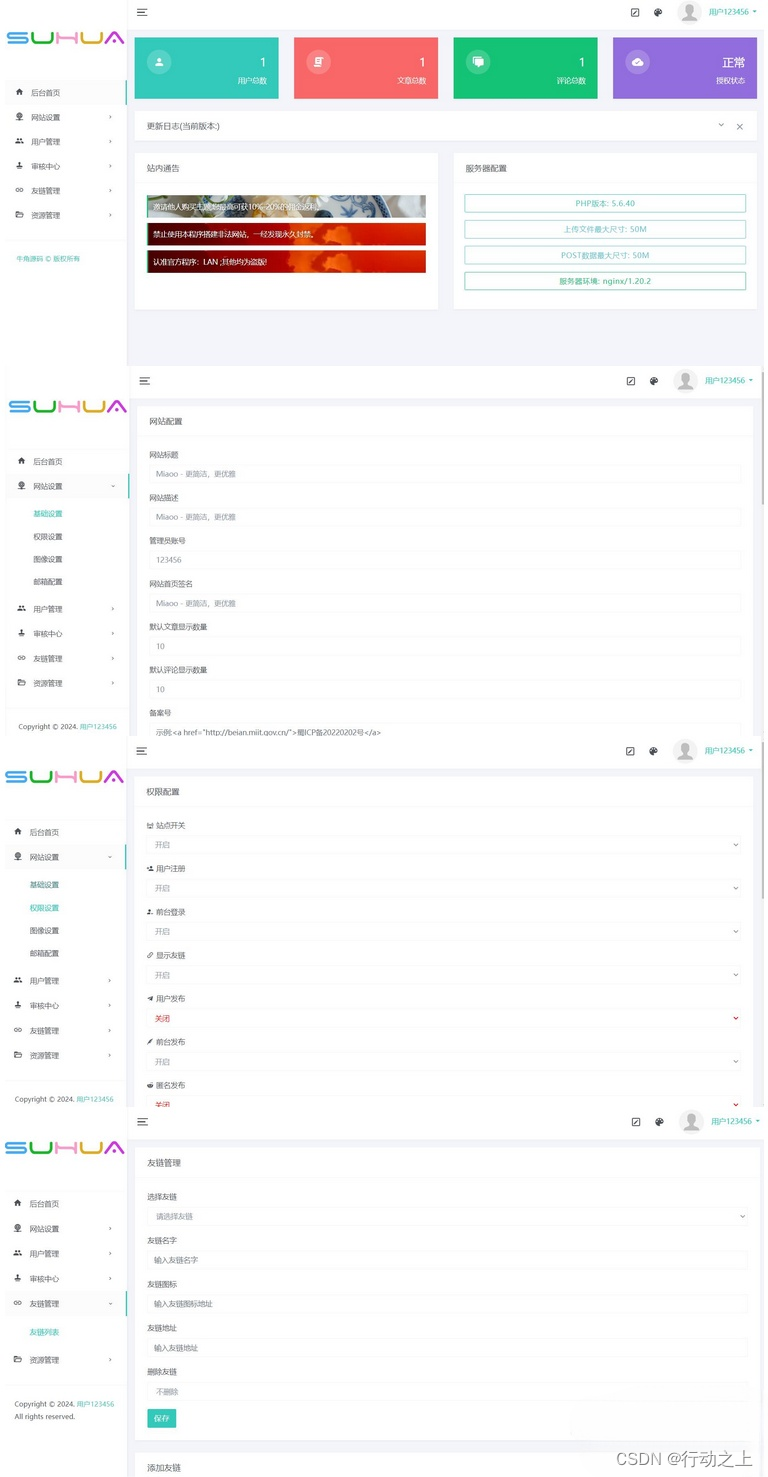
朋友圈程序全开源版源码,附带系统搭建教程
前台一键发布图文,视频,音乐。发布内容支持定位或自定义位置信息。支持将发布内容设为广告模式消息站内通知或邮件通知。支持其他用户注册,支持其他用户发布文章,管理自己的文章。拥有丰富的后台管理功能,一键操作。安装环境 Nginx ≥1.22 …...

思维方式系列文章目录 -《清单革命》实践
思维方式系列文章目录 -《清单革命》 文章目录 思维方式系列文章目录 -《清单革命》前言一、《清单革命》思维导图二、清单制作原则 前言 请记住,现在开始心灵转变,人人都会犯错,而错误分为:无知之错、无能之错。 无知之错&#…...

RAID 创建使用以及ubuntu安装和使用zfs文件系统及Ubuntu软件安装
RAID 创建使用 部署 RAID 10 的学习 1. 搭建 RAID 10 就是 RAID 1 加上 RAID 0,准备四块磁盘,用于创建 RAID 10,配置vmware虚拟机,创建四个虚拟硬盘。 2. 检查磁盘信息 rootubuntu:~# ls /dev/sd* /dev/sda /dev/sda1 /dev/sda2 /dev/sda3 /dev/s…...

yarn常用命令小记
安装 npm install -g yarn查看版本 yarn -v初始化项目与依赖管理 yarn init:与npm init一样通过交互式会话生成一个新的package.jason文件以初始化项目;跳过会话可使用yarn init --yes,简写yarn init -yyarn add <package><versi…...
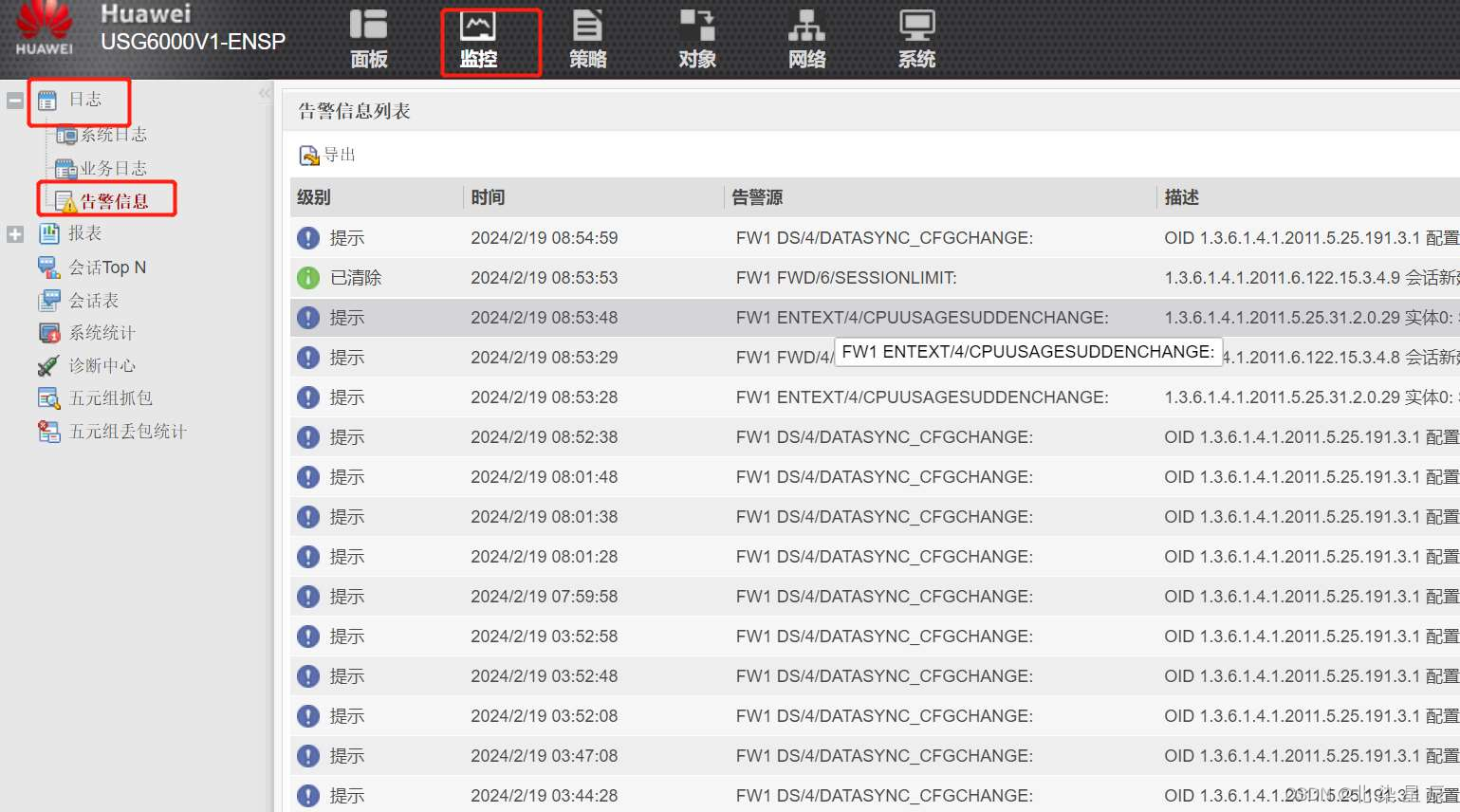
防御保护---内容保护
文章目录 目录 文章目录 一.防火墙内容安全概述 二.深度识别技术(DFI/DPI) 深度包检测技术(DPI) 深度流检测技术(DFI) 两者区别 三.入侵防御IPS 一.防火墙内容安全概述 防火墙内容安全是防火墙的一个重…...

jquery将网页html文档导出为pdf图片
jquery将网页html文档导出为pdf图片 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content&q…...
opengl 学习着色器
一.GLSL 着色器是使用一种叫GLSL的类C语言写成的。GLSL着色器编码顺序:声明版本》定义输入输出》uniform》main函数。每个着色器的入口点是main函数,在main函数中我们处理所有的输入变量,并将结果输出到输出变量中。如下图: #ver…...
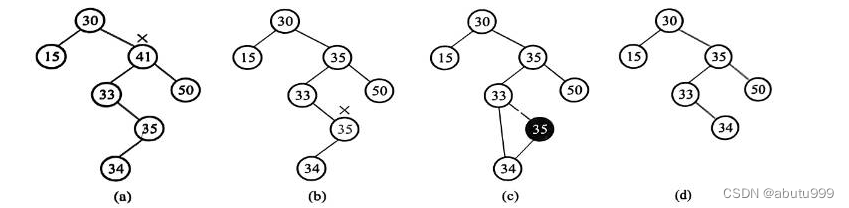
【数据结构】18 二叉搜索树(查找,插入,删除)
定义 二叉搜索树也叫二叉排序树或者二叉查找树。它是一种对排序和查找都很有用的特殊二叉树。 一个二叉搜索树可以为空,如果它不为空,它将满足以下性质: 非空左子树的所有键值小于其根节点的键值非空右子树的所有键值都大于其根结点的键值左…...
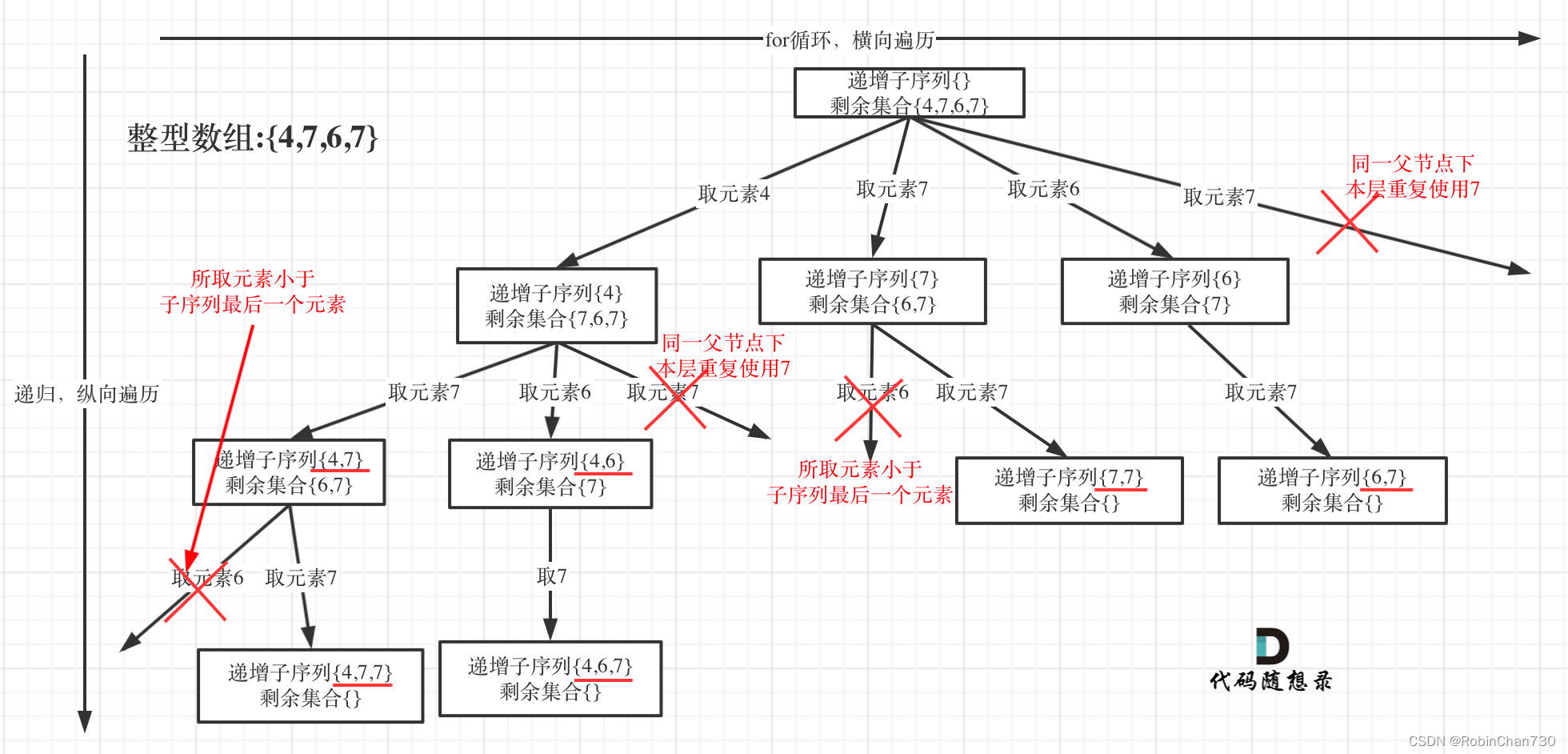
力扣日记2.20-【回溯算法篇】491. 非递减子序列
力扣日记:【回溯算法篇】491. 非递减子序列 日期:2023.2.20 参考:代码随想录、力扣 ps:放了个寒假,日记又搁置了三星期……(下跪忏悔) 491. 非递减子序列 题目描述 难度:中等 给你一…...
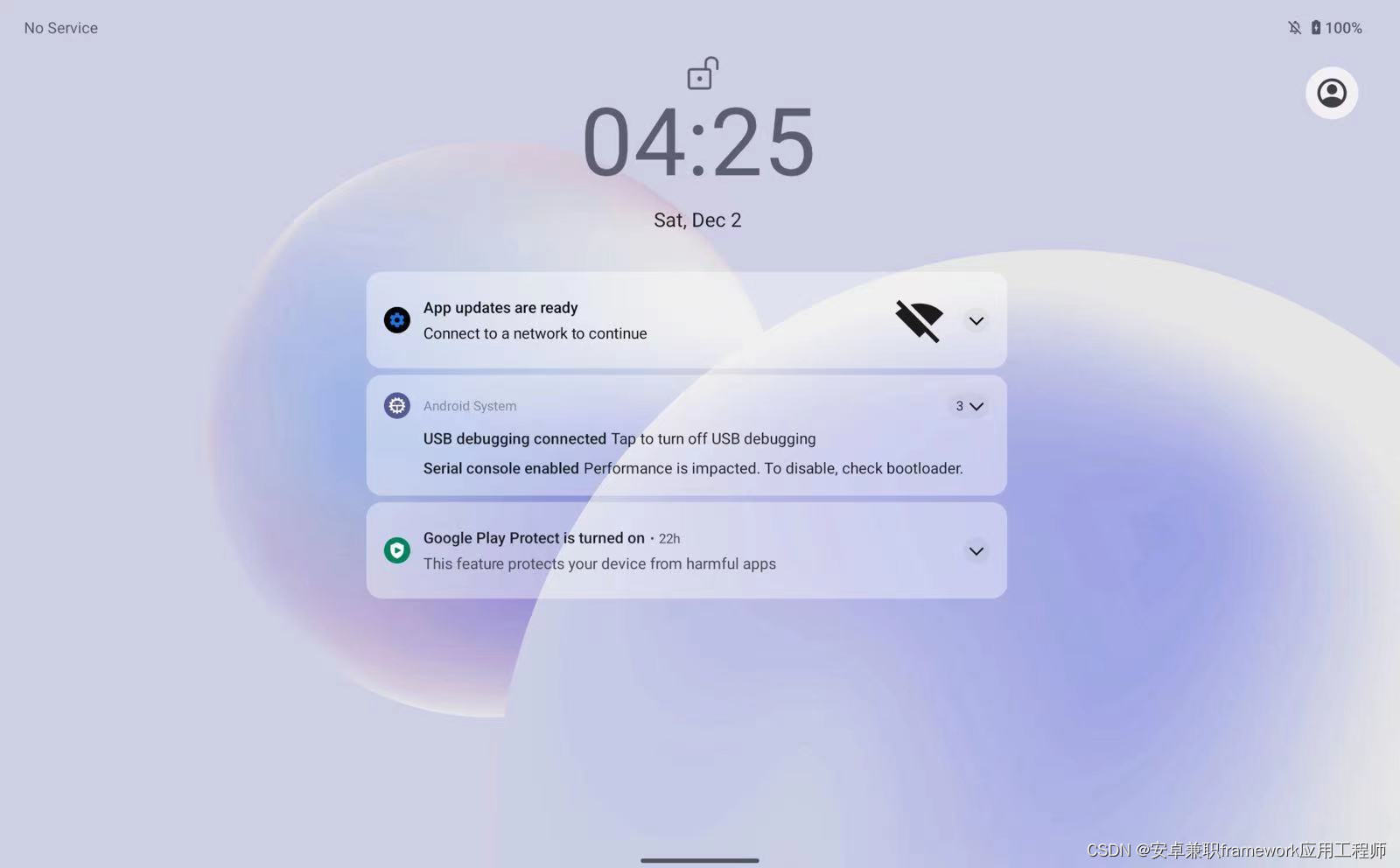
Android 13.0 SystemUI下拉状态栏定制二 锁屏页面横竖屏解锁图标置顶显示功能实现
1.前言 在13.0的系统rom定制化开发中,在关于systemui的锁屏页面功能定制中,由于在平板横屏锁屏功能中,时钟显示的很大,并且是在左旁边居中显示的, 由于需要和竖屏显示一样,所以就需要用到小时钟显示,然后同样需要居中,所以就来分析下相关的源码,来实现具体的功能 如图…...
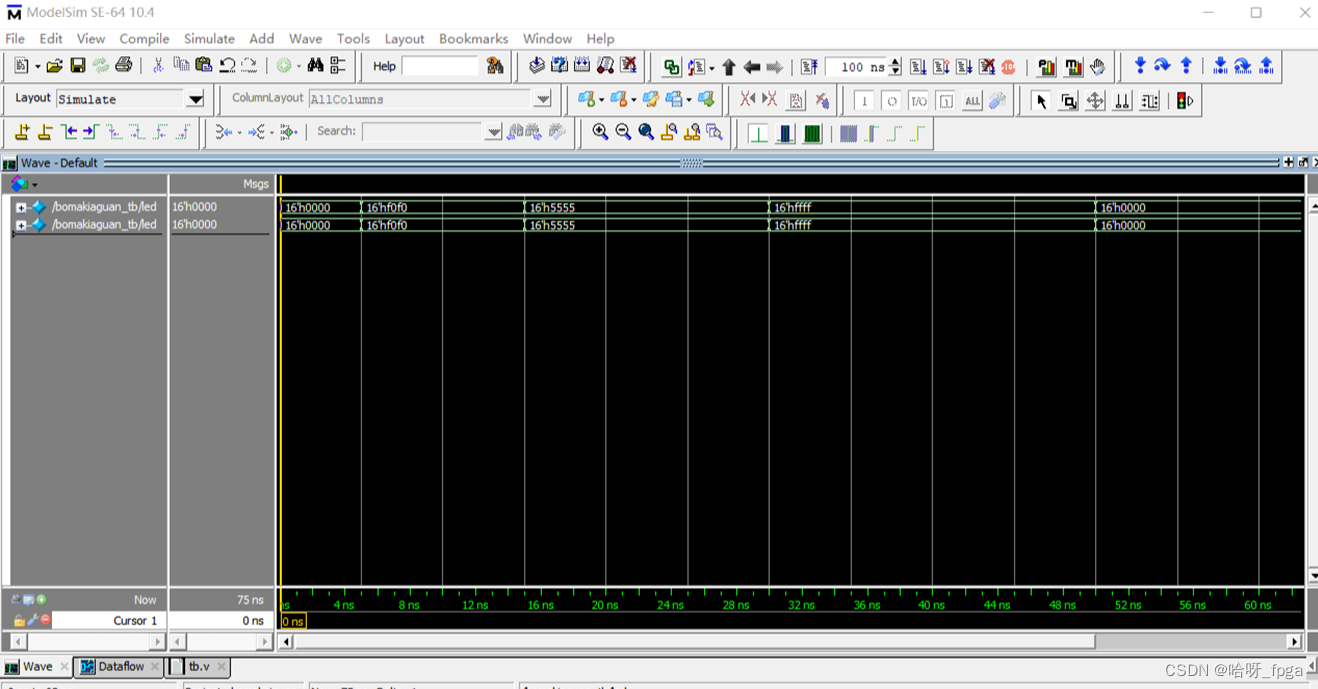
FPGA_简单工程_拨码开关
一 框图 二 波形图 三 代码 3.1 工程代码 module bomakiaguan (input [15:0] switch, // 输入16路拨码开关output reg [15:0] led // 输出16个LED灯 );always (switch) beginled < switch; // 将拨码开关的值直接赋给LED灯 end // 将拨码开关的值直接赋给LED灯 endmodu…...

LaunchPad 市场的复苏,Penpad 成新兴生力军
以 Fair Launch 为主要启动方式的铭文市场的爆发,推动了 LaunchPad 市场的复苏,绝多数所铭文项目都能通过 Fairr Launch 的方式筹集资金实现启动,该赛道的爆发不仅推动了数百亿美元的热钱开始在链上不断涌动,同时也进一步形成了新…...
知识图谱实战应用30-基于py2neo的天文学中的恒星、行星与卫星之间的关系知识图谱研究与应用
大家好,我是微学AI,今天给大家介绍一下知识图谱实战应用30-基于py2neo的天文学中的恒星、行星与卫星之间的关系知识图谱研究与应用。本文将详细介绍如何利用py2neo构建天文学中的恒星、行星与卫星之间的关系知识图谱,并探讨其在天文学研究中的应用。文章将提供多条太阳系中恒…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
