【数据结构】18 二叉搜索树(查找,插入,删除)
定义
二叉搜索树也叫二叉排序树或者二叉查找树。它是一种对排序和查找都很有用的特殊二叉树。
一个二叉搜索树可以为空,如果它不为空,它将满足以下性质:
- 非空左子树的所有键值小于其根节点的键值
- 非空右子树的所有键值都大于其根结点的键值
- 左、右子树都是二叉树
动态查找
查找操作Find
在二叉搜索树中查找关键字为X的结点,返回其所在结点的地址。查找过程如下:
- 查找从树的根节点开始,若树为空,返回NULL
- 搜索树非空,则根节点关键字和X比较,依据结果,需要进行不同的处理
若根节点键值小于X,在根节点右子树中查找
若根节点的键值大于X,在根节点的左子树中查找
若两者比较结果相等,搜索完成。
递归代码
Position Find_RE(BinTree BT, ElementType X) {if (!BT) {return NULL;}if (X > BT->Data) {return Find_RE(BT->Right, X);}else if(X < BT->Data){return Find_RE(BT->Left, X);}else{return BT;}
}
迭代函数
Position Find_D(BinTree BT, ElementType X) {BinTree T = BT;while (T) {if (T->Data > X) {T = T->Left;}else if (T->Data < X) {T = T->Right;}else{return T;}}
}
查找最大和最小元素
根据二叉搜索树的性质,最大元素一定在最右分支的尾端,最小元素一定在最左分支的尾端。
递归函数
Position FindMin(BinTree BT) {if (!BT) {return NULL;}else if(!BT->Left){return BT;}else{return FindMin(BT->Left);}
}
迭代函数
Position FindMinD(BinTree BT) {BinTree T = BT;while (T->Left) {T = T->Left;}return T;
}
找最大值只需要把left换成right
插入
BinTree Insert(BinTree BT, ElementType X) {if (!BT) {BT = (BinTree)malloc(sizeof(struct TNode));BT->Data = X;BT->Left = BT->Right = NULL;}else {if (X > BT->Data) {BT->Right = Insert(BT->Right, X);}else if (X < BT->Data) {BT->Left = Insert(BT->Left, X);}}return BT;
}
删除
二叉搜索树的删除比较复杂,需要考虑节点的位置
- 叶结点
可以直接删除,将其父节点指针置空即可。 - 只有一个孩子结点
要修改其父节点的指针,指向要删除结点的孩子结点。 - 有左、右两颗树
究竟用哪颗子树的根结点来填充删除节点的位置?有两种选择方式:选择左子树的最大元素,或者选择右子树的最小元素。无论哪种方式,最后被选择的结点必定最多只有一个孩子。
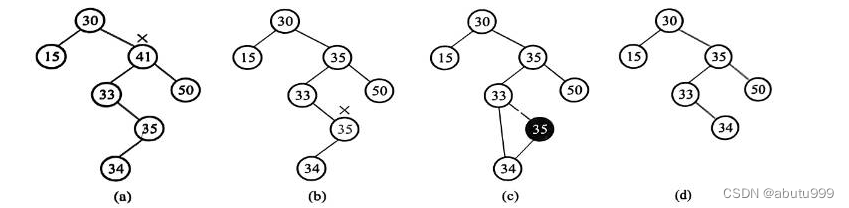
采用右子树的最小元素的删除代替策略。
代码思路: 先找到要删除元素的位置,若其具有左右子树,找到该位置的右子树里面的最小元素,赋值到该位置上,在其右子树中删除最小元素(递归调用),若只有一个子树或者没有,易操作。
BinTree DeleteBT(BinTree BT, ElementType X) {Position p;if (!BT) {printf("can't find the node\n");}else {if (X > BT->Data) {BT->Right = DeleteBT(BT->Right, X);}else if (X < BT->Data) {BT->Left = DeleteBT(BT->Left, X);}else {if (BT->Left && BT->Right) {//FIND THE Min OF Right TREEp = FindMin(BT->Right);BT->Data = p->Data;BT->Right = DeleteBT(BT->Right, p->Data);}else {p = BT;if (!BT->Left) {BT = BT->Right;}else { BT = BT->Left; }free(p);}}}return BT;
}
相关文章:

【数据结构】18 二叉搜索树(查找,插入,删除)
定义 二叉搜索树也叫二叉排序树或者二叉查找树。它是一种对排序和查找都很有用的特殊二叉树。 一个二叉搜索树可以为空,如果它不为空,它将满足以下性质: 非空左子树的所有键值小于其根节点的键值非空右子树的所有键值都大于其根结点的键值左…...
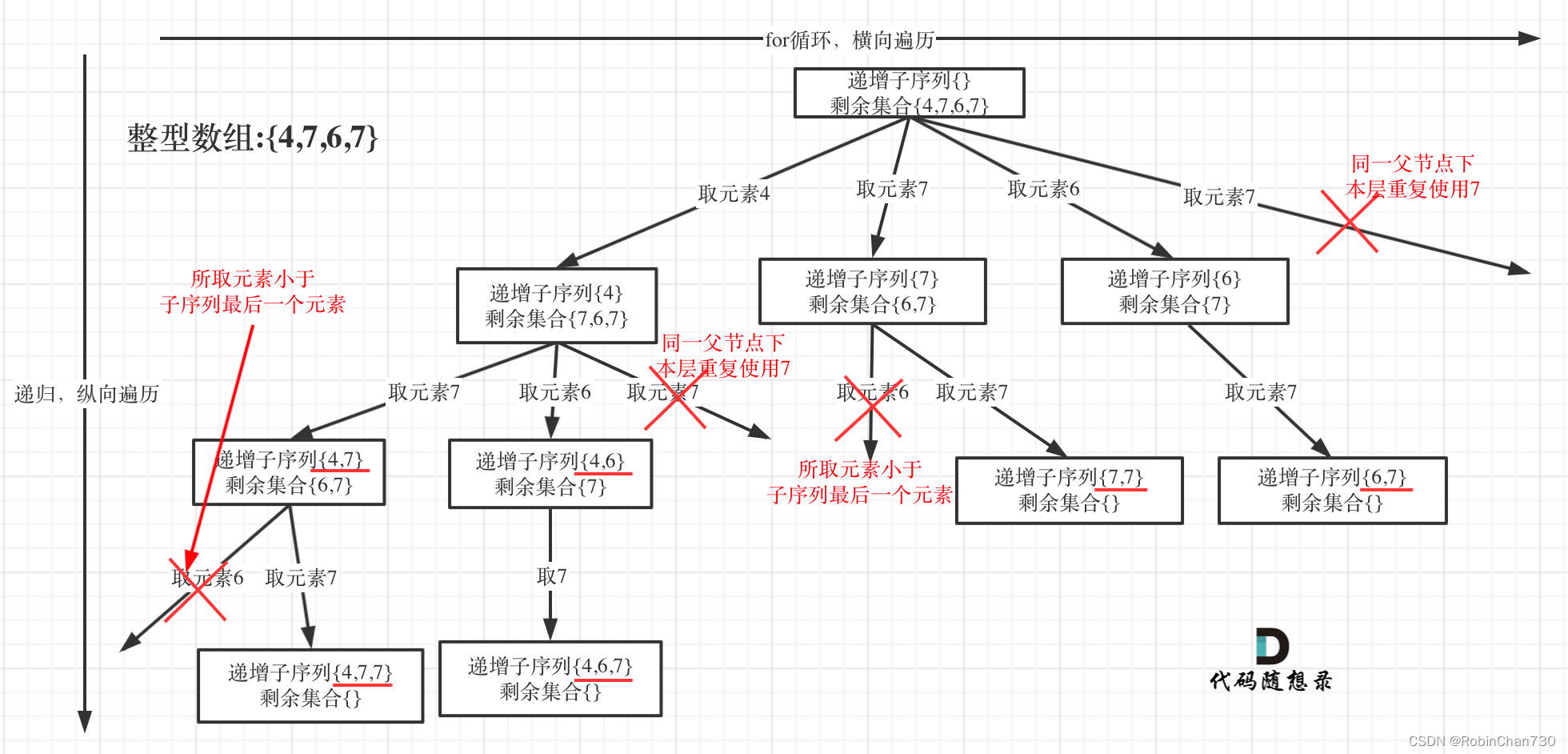
力扣日记2.20-【回溯算法篇】491. 非递减子序列
力扣日记:【回溯算法篇】491. 非递减子序列 日期:2023.2.20 参考:代码随想录、力扣 ps:放了个寒假,日记又搁置了三星期……(下跪忏悔) 491. 非递减子序列 题目描述 难度:中等 给你一…...
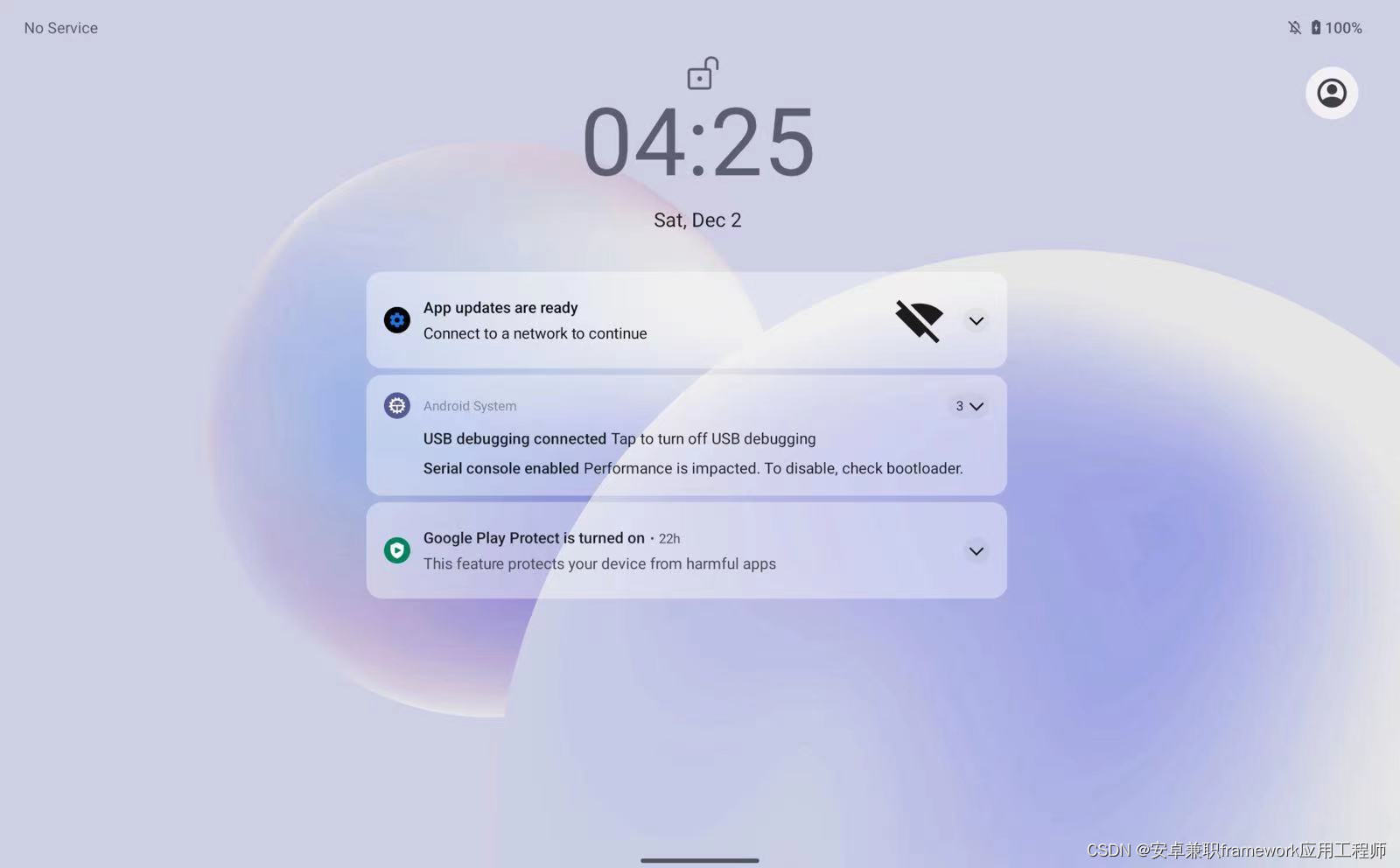
Android 13.0 SystemUI下拉状态栏定制二 锁屏页面横竖屏解锁图标置顶显示功能实现
1.前言 在13.0的系统rom定制化开发中,在关于systemui的锁屏页面功能定制中,由于在平板横屏锁屏功能中,时钟显示的很大,并且是在左旁边居中显示的, 由于需要和竖屏显示一样,所以就需要用到小时钟显示,然后同样需要居中,所以就来分析下相关的源码,来实现具体的功能 如图…...
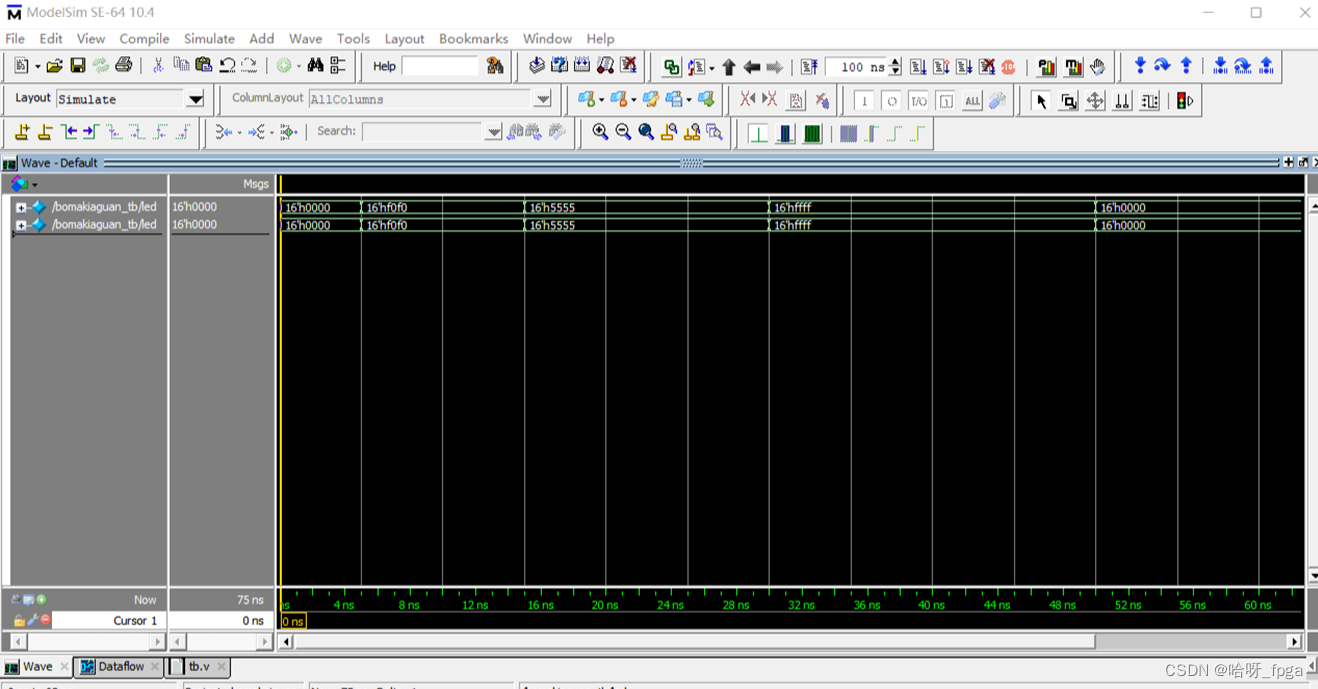
FPGA_简单工程_拨码开关
一 框图 二 波形图 三 代码 3.1 工程代码 module bomakiaguan (input [15:0] switch, // 输入16路拨码开关output reg [15:0] led // 输出16个LED灯 );always (switch) beginled < switch; // 将拨码开关的值直接赋给LED灯 end // 将拨码开关的值直接赋给LED灯 endmodu…...

LaunchPad 市场的复苏,Penpad 成新兴生力军
以 Fair Launch 为主要启动方式的铭文市场的爆发,推动了 LaunchPad 市场的复苏,绝多数所铭文项目都能通过 Fairr Launch 的方式筹集资金实现启动,该赛道的爆发不仅推动了数百亿美元的热钱开始在链上不断涌动,同时也进一步形成了新…...
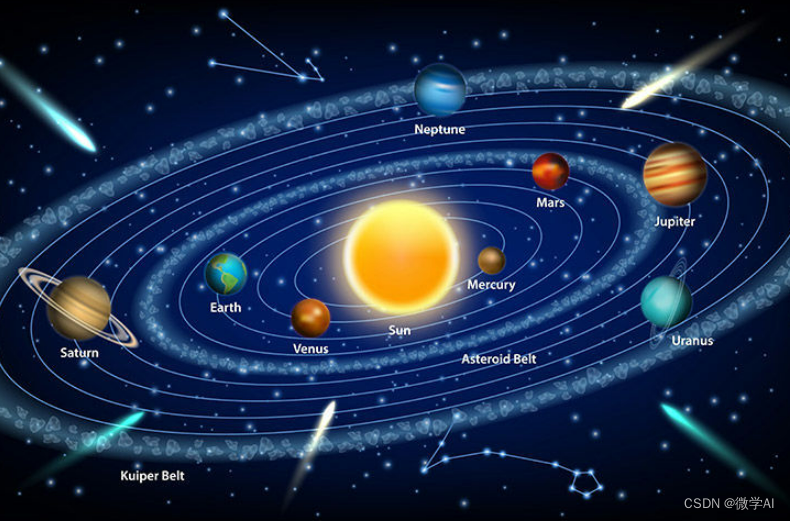
知识图谱实战应用30-基于py2neo的天文学中的恒星、行星与卫星之间的关系知识图谱研究与应用
大家好,我是微学AI,今天给大家介绍一下知识图谱实战应用30-基于py2neo的天文学中的恒星、行星与卫星之间的关系知识图谱研究与应用。本文将详细介绍如何利用py2neo构建天文学中的恒星、行星与卫星之间的关系知识图谱,并探讨其在天文学研究中的应用。文章将提供多条太阳系中恒…...

笔试题详解(C语言进阶)
前言 欢迎阅读本篇文章!本篇文章通过一个笔试题来加强我们对C语言的理解,希望对你有帮助。后续我会写一个栏目,集合我见到的C语言题目,进行分析讲解。 1、题目一 判断下面程序的输出结果:(下面说的地址4/8字节是因为对…...
ClickHouse快速上手
简介 ClickHouse是一个用于联机分析(OLAP)的列式数据库管理系统(DBMS) 官网(https://clickhouse.com/docs/zh)给出的定义,其实没看懂 特性 ClickHouse支持一种基于SQL的声明式查询语言,它在许多情况下与ANSI SQL标准相同。使用时和MySQL有点相似&#…...
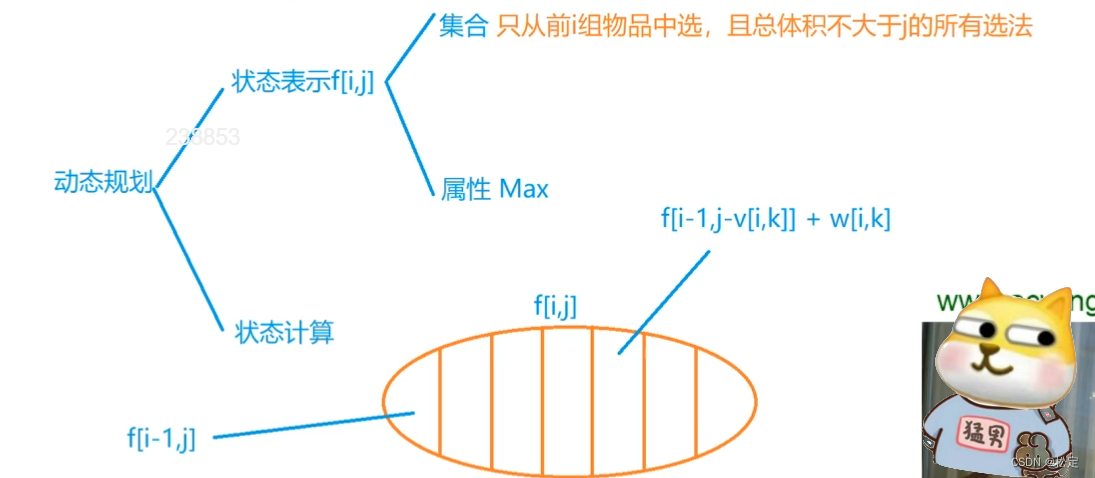
蓝桥杯DP算法——背包问题(C++)
目录 一、01背包问题 二、完全背包问题 三、多重背包问题 四、多重背包问题(优化版) 五、分组背包问题 一、01背包问题 01背包问题就是有N件物品,一个空间大小为V的背包,每个物品只能使用一次,使得背包中所装物品…...

【LeetCode+JavaGuide打卡】Day22|235. 二叉搜索树的最近公共祖先、701.二叉搜索树中的插入操作、450.删除二叉搜索树中的节点
学习目标: 235. 二叉搜索树的最近公共祖先 701.二叉搜索树中的插入操作 450.删除二叉搜索树中的节点 学习内容: 235. 二叉搜索树的最近公共祖先 题目链接&&文章讲解 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最…...

Stable Diffusion WebUI 界面介绍
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 大家好,我是水滴~~ 本文主要对 Stable Diffusion WebUI 的界面进行简单的介绍,让你对该 WebUI 有个大致的了解,为后面的深入学习打下一个基础。主要内容包括:Stable Diffusion 模型(Stable Diffusion checkp…...
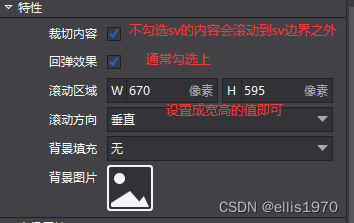
Cocos2dx-lua ScrollView[一]基础篇
一.ScrollView概述 cocos游戏中ScrollView控件大量使用,95%以上的项目都会使用ScrollView,个别游戏可能全部使用翻页的滑动效果。如果想要精通Cocos的UI开发,精通ScrollView控件非常关键,因此对ScrollView的使用进行总结很有必要。 下文缩写说明:sv = ScrollView, item代…...

QT应用软件【协议篇】周立功CAN接口卡代码示例
文章目录 USBCAN系列CAN接口卡规格参数资料下载QT引用周立功的库安装sdk代码USBCAN系列CAN接口卡 USBCAN系列CAN接口卡兼容USB2.0全速规范,可支持1/2/4/8路CAN接口。采用该接口卡,PC机可通过USB连入CAN网络,进行CAN总线数据采集和处理,主要具备以下几大优势特点: 支持车载…...
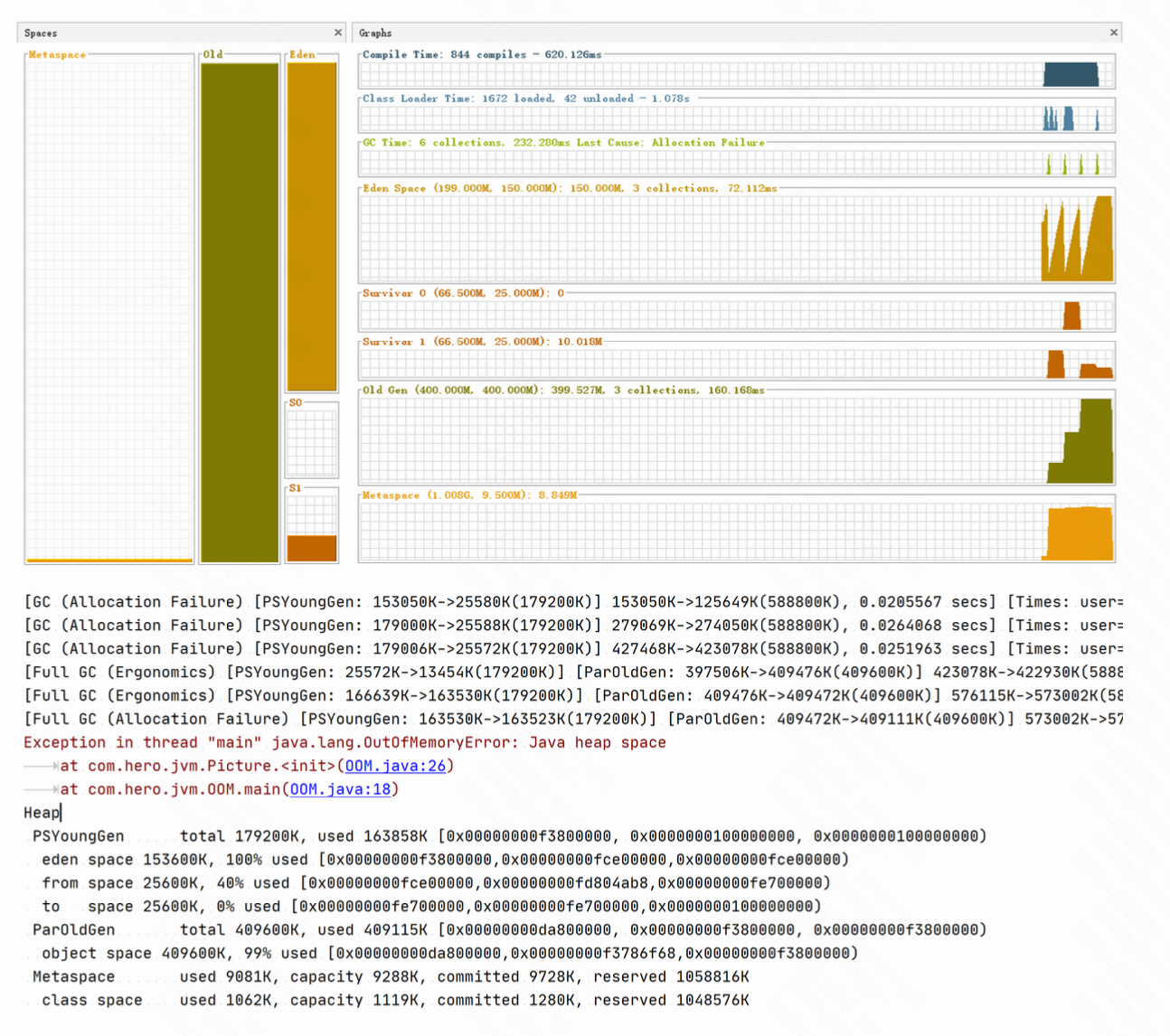
JVM对象的创建流程与内存分配
对象的创建流程与内存分配 创建流程对象内存分配方式内存分配安全问题对象内存分配流程【重要】:对象怎样才会进入老年代?重点 案例演示:对象分配过程大对象直接进入老年代02-对象内存分配的过程: 创建流程 加载 验证 解析 准备 初始化 使用 写在 对象内存分配方式 内存分配…...
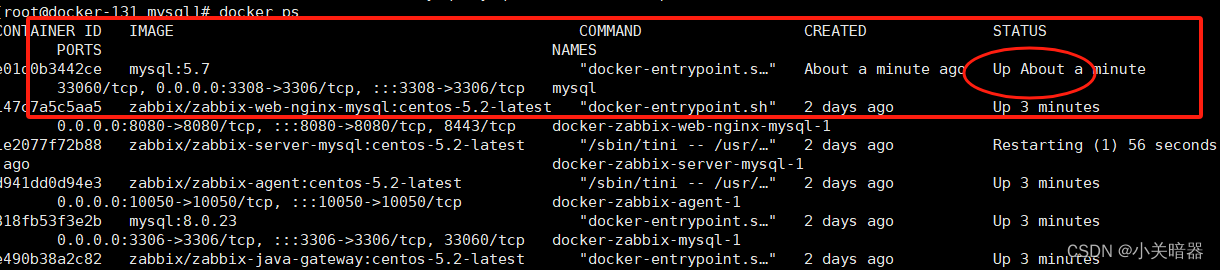
docker (六)-进阶篇-数据持久化最佳实践MySQL部署
容器的数据挂载通常指的是将宿主机(虚拟机或物理机)上的目录或文件挂载到容器内部 MySQL单节点安装 详情参考docker官网文档 1 创建对应的数据目录、日志目录、配置文件目录(参考二进制安装,需自己建立数据存储目录) mkdir -p /data/mysq…...
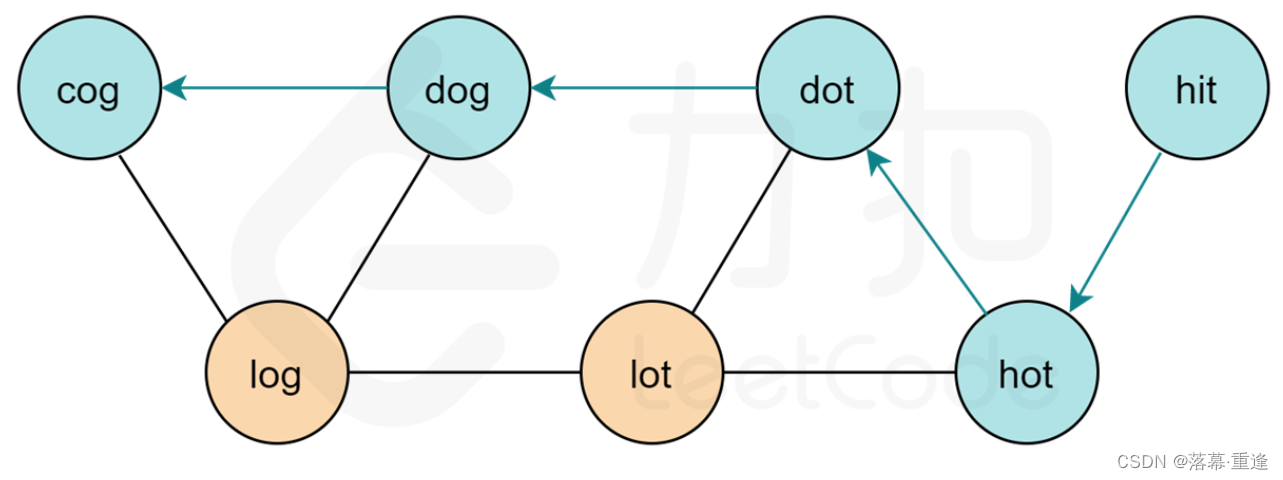
力扣题目训练(17)
2024年2月10日力扣题目训练 2024年2月10日力扣题目训练551. 学生出勤记录 I557. 反转字符串中的单词 III559. N 叉树的最大深度241. 为运算表达式设计优先级260. 只出现一次的数字 III126. 单词接龙 II 2024年2月10日力扣题目训练 2024年2月10日第十七天编程训练,今…...

【react】react中和vue中的provide/inject、context写法示例
react写法 在 React 中,provide和inject的功能类似于 Vue.js 中的 provide和inject。它们都是用于跨组件层次传递数据的。 在 React 中,没有内置的 provide 和 inject 函数。但是,你可以使用 React 的 Context 来实现类似的功能。 Context…...
)
MySQL 的存储引擎(基本介绍)
文章目录 前言MySQL 的存储引擎介绍存储引擎是什么?存储引擎的特性? Innodb 与 Mylsam 的区别行级锁与表级锁是否支持事务是否支持恢复数据是否支持外键是否支持 MVCC 总结 前言 好文章不要错过,前两天跟大家分享的文章 1.MySQL的基础架构 2.SQL语句的…...

Unity3D 实现基于物理引擎的绳子关节解析详解
前言 在游戏开发中,有时候我们需要实现绳子关节效果,比如在射击游戏中射击绳子,或者在平衡游戏中使用绳子作为支撑。本文将详细介绍如何使用Unity3D的物理引擎实现绳子关节效果。 对惹,这里有一个游戏开发交流小组,希…...
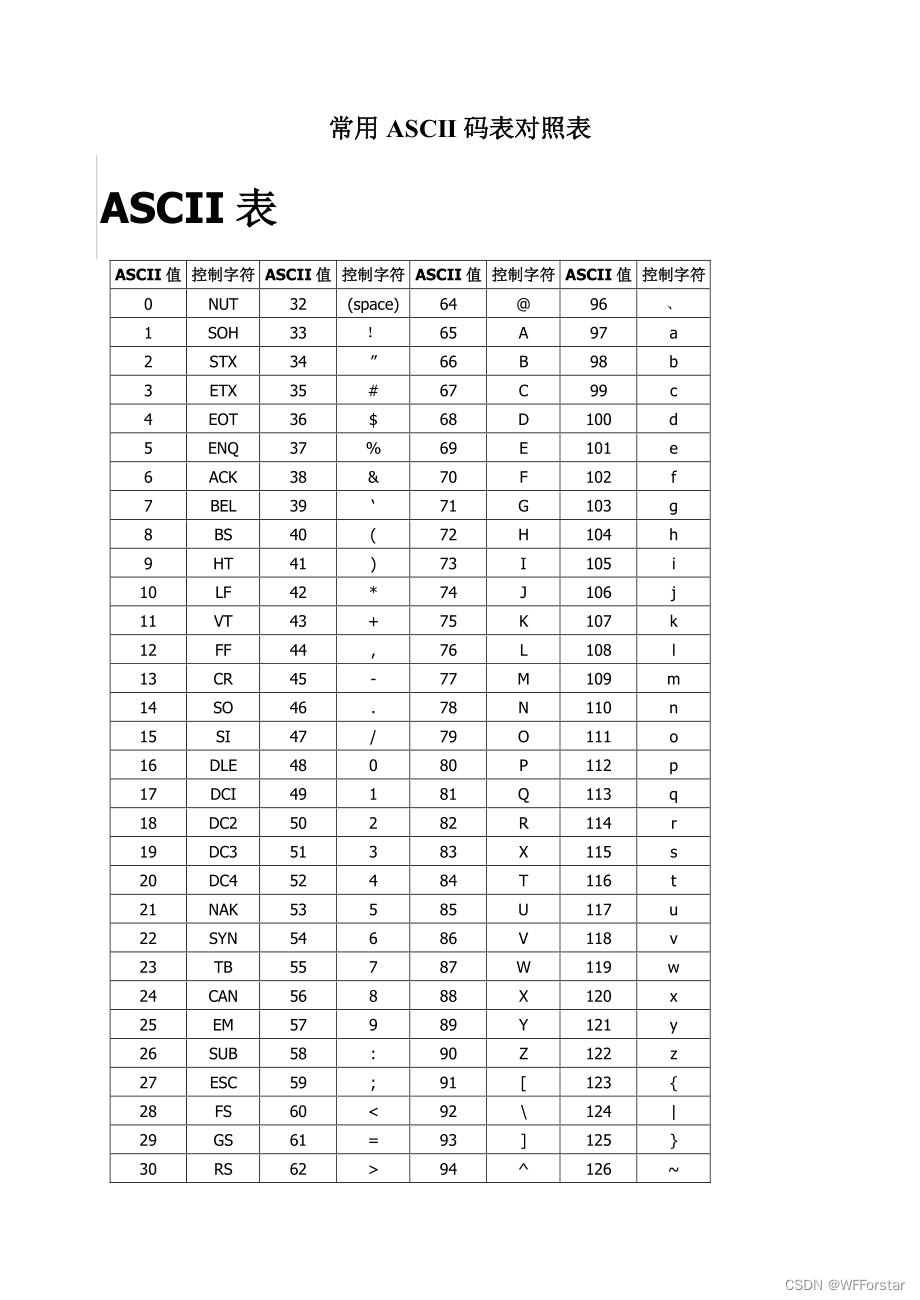
C语言二级易忘易错易混知识点(自用)
1.数组名不能自加。 因为数组名实际上是一个指针,指向数组的第一个元素的地址。数组名在编译器中被视为常量,它的值是固定的,不能改变。 要访问数组的不同元素,应该使用数组名加上偏移量的方式来访问。 2.共用体只有最后一次赋值…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
