【LeetCode】70. 爬楼梯(简单)——代码随想录算法训练营Day38
题目链接:70. 爬楼梯
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
提示:
1 <= n <= 45
文章讲解:代码随想录
视频讲解:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题解1:动态规划
思路:1个台阶有1种走法,2个台阶有2种走法(1+1和2)。3个台阶可以看成在1个台阶的走法上再走2步,或者在2个台阶的走法上再走1步;4个台阶可以看成在3个台阶的走法上再走2步,或者在2个台阶的走法上再走1步。即 n 个台阶的走法可以看成在 n - 2个台阶的走法上再走2步,或者在 n - 1个台阶的走法上再走1步。因此可以用动态规划求解。
动态规划分析:
- dp 数组以及下标的含义:dp[i] 为 i 个台阶的走法。
- 递推公式:dp[i] = dp[i - 1] + dp[i - 2]。
- dp 数组初始化:dp[0] 没有意义,dp[1] = 1,dp[2] = 2。
- 遍历顺序:从前向后。
- 打印 dp 数组:1、2、3、5、......
/*** @param {number} n* @return {number}*/
var climbStairs = function(n) {const dp = new Array(n + 1);dp[1] = 1; // 1个台阶有1种走法dp[2] = 2; // 2个台阶有2种走法for (let i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2]; // i 个台阶有 dp[i - 1] + dp[i - 2] 种走法}return dp[n];
};分析:时间复杂度为 O(n),空间复杂度为 O(n)。
题解2:动态规划优化
思路:i 个台阶的走法依赖于 i - 1 和 i - 2 个台阶的走法,可以用两个变量存储,在循环中更新这2个变量。
/*** @param {number} n* @return {number}*/
var climbStairs = function(n) {if (n <= 2) {return n; // 1个台阶有1种走法,2个台阶有2种走法}let a = 1, b = 2; // a 为 i - 2个台阶的走法,b 为 i - 1 个台阶的走法for (let i = 3; i <= n; i++) {const c = a + b; // i 个台阶有 dp[i - 1] + dp[i - 2] 种走法a = b; // 更新 ab= c; // 更新 b}return b; // b 即为最终答案
};分析:时间复杂度为 O(n),空间复杂度为 O(1)。
收获
当一个问题的答案依赖于较小的问题的答案时,可以使用动态规划法来求解。练习使用动态规划法解决问题,按照5部曲来分析。本题实际上是一个斐波那契数列。
相关文章:
——代码随想录算法训练营Day38)
【LeetCode】70. 爬楼梯(简单)——代码随想录算法训练营Day38
题目链接:70. 爬楼梯 题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1: 输入:n 2 输出:2 解释:有两种方法可以爬到…...
)
图数据库 之 Neo4j - Cypher语法基础(5)
节点(Nodes) Cypher使用()来表示一个节点。 () # 最简单的节点形式,表示一个任意无特征的节点,其实就是一个空节点(movie) # 如果想指向一个节点在其他地方,我们可以给节点添加一个变量名(如movie),表示一个变量名为 movie的节点。(:Movie) # 表示一个标签为 Movie 的匿名…...

打造智能物品租赁平台:Java与SpringBoot的实践
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...

盘点那些世界名校计算机专业采用的教材
清华、北大、MIT、CMU、斯坦福的学霸们在新学期里要学什么?今天我们来盘点一下那些世界名校计算机专业采用的教材。 书单目录 1.《深入理解计算机系统》(原书第3版)2. 《算法导论》(原书第3版)3. 《计算机程序的构造和…...

编程笔记 Golang基础 013 格式化输入输出
编程笔记 Golang基础 013 格式化输入输出 一、格式化输出1. fmt.Print系列函数2. Printf格式说明3. 格式化布尔类型 二、格式化输入1. fmt.Scan系列函数注意事项 三、练习小结 Go语言中的格式化输入和输出主要通过标准库 fmt 包来实现。主要是输出需要格式化。 一、格式化输出 …...

身份证实名认证接口-简单的身份认证API调用方法
还在为复杂的API调用头疼不已?今天为大家带来一种超简单的身份认证API调用方法,让你的工作效率瞬间起飞! Java调用代码如下: import java.io.*; import okhttp3.*; public class main { public static void main(String []ar…...
数据结构·顺序表
1数据结构简介 学习数据结构与算法之前,一般是先学数据结构,方便之后学习算法,那么数据结构拆开介绍,就是数据 和 结构,数据,生活中到处都是,结构,就是数据存储的方式,即…...
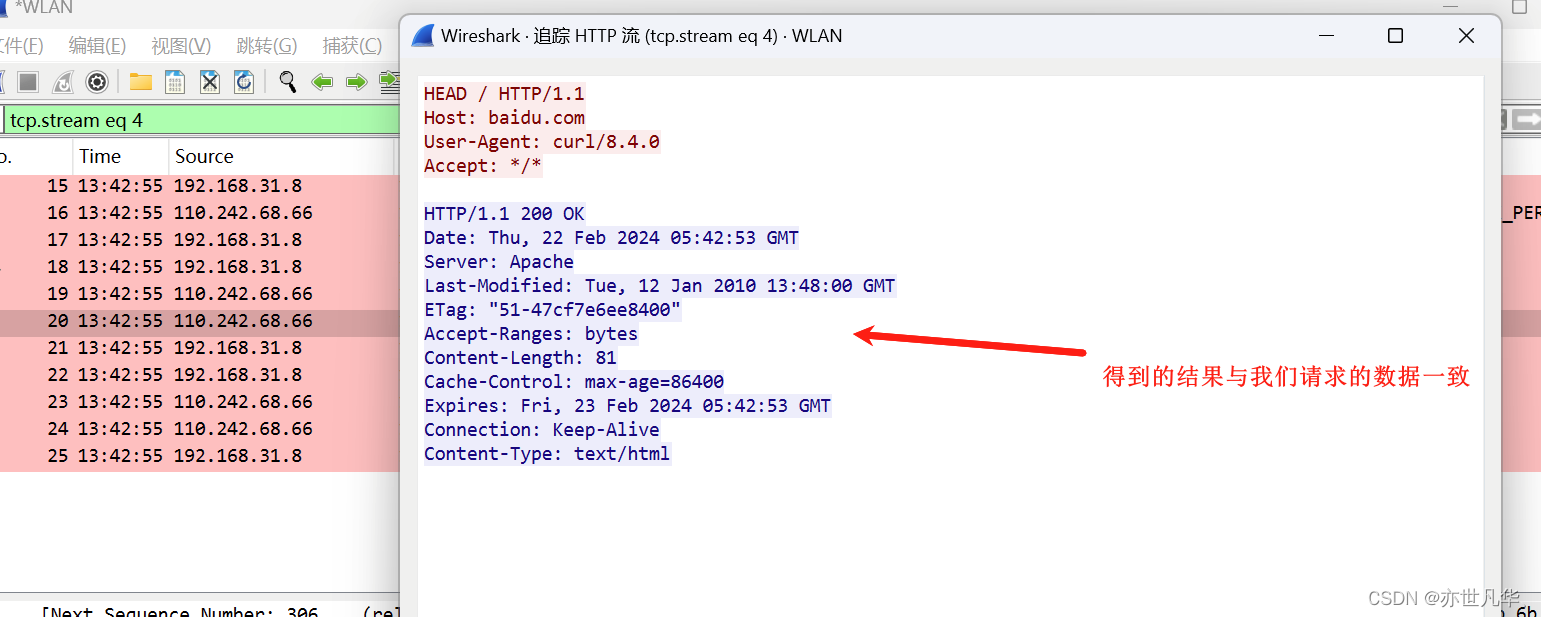
玩转网络抓包利器:Wireshark常用协议分析讲解
Wireshark是一个开源的网络协议分析工具,它能够捕获和分析网络数据包,并以用户友好的方式呈现这些数据包的内容。Wireshark 被广泛应用于网络故障排查、安全审计、教育及软件开发等领域。关于该工具的安装请参考之前的文章:地址 ,…...
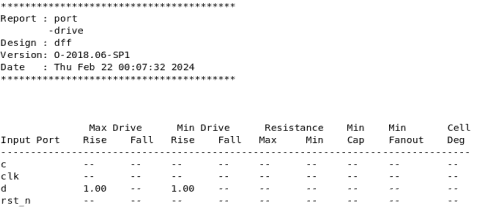
静态时序分析:SDC约束命令set_drive详解
相关阅读 静态时序分析https://blog.csdn.net/weixin_45791458/category_12567571.html 本章将讨论使用set_drive命令,它用于对输入端口的驱动能力建模。首先需要说明的是,默认情况下,DC在STA时默认输入端口的转换时间是0,这对于…...

C#算法(12)—对图像像素做X/Y方向的偏移
我们在上位机开发领域有时候需要对获取的图像的像素做整体的偏移,比如所有像素在X方向上偏移几个像素,或者所有像素在Y方向上偏移几个像素,本文就是开发了像素整体偏移算法来解决这个问题。 比如有一个图像大小为3*3,像素值如下图1,如果我想实现将这个幅图像的像素整体往右…...
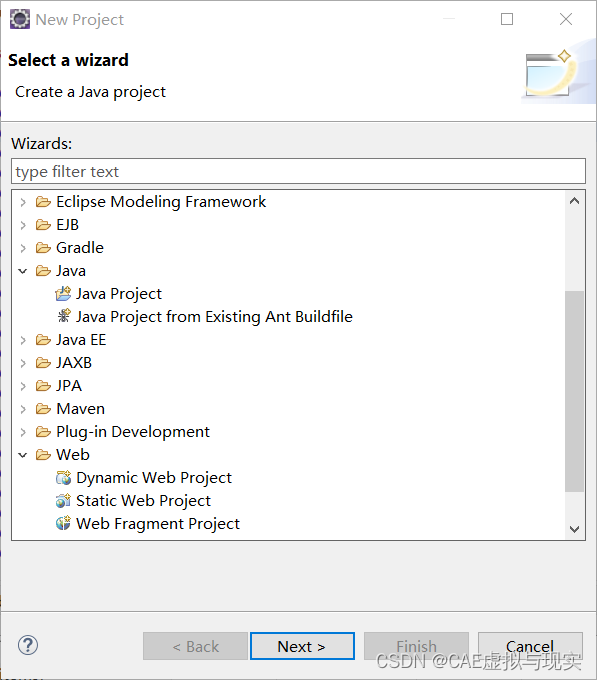
说一说Eclipse的项目类型和常用项目的区别
Eclipse在新建项目的时候有很多类型,包括Java project、Web project等等,如下: 那么这些项目类型有什么区别呢?我们在创建项目的时候应该如何选择,了解清楚这一点还是非常重要的,但记住一个出发点ÿ…...

[opencv][windows]cmake opencv opencv_contrib所需的缓存文件下载
这个是windows上源码编译opencvopencv-contrib时候cmake时候缓存文件,只需要将压缩文件夹解压到源码目录下面,cmake-gui上configure时候就不会报错,注意解压后文件夹名字是.cache,文件夹名字不能改变,比如opencv/.cache,有的人解压…...
五步解决 Ubuntu 18.04 出现GLIBC_2.28 not found的解决方法
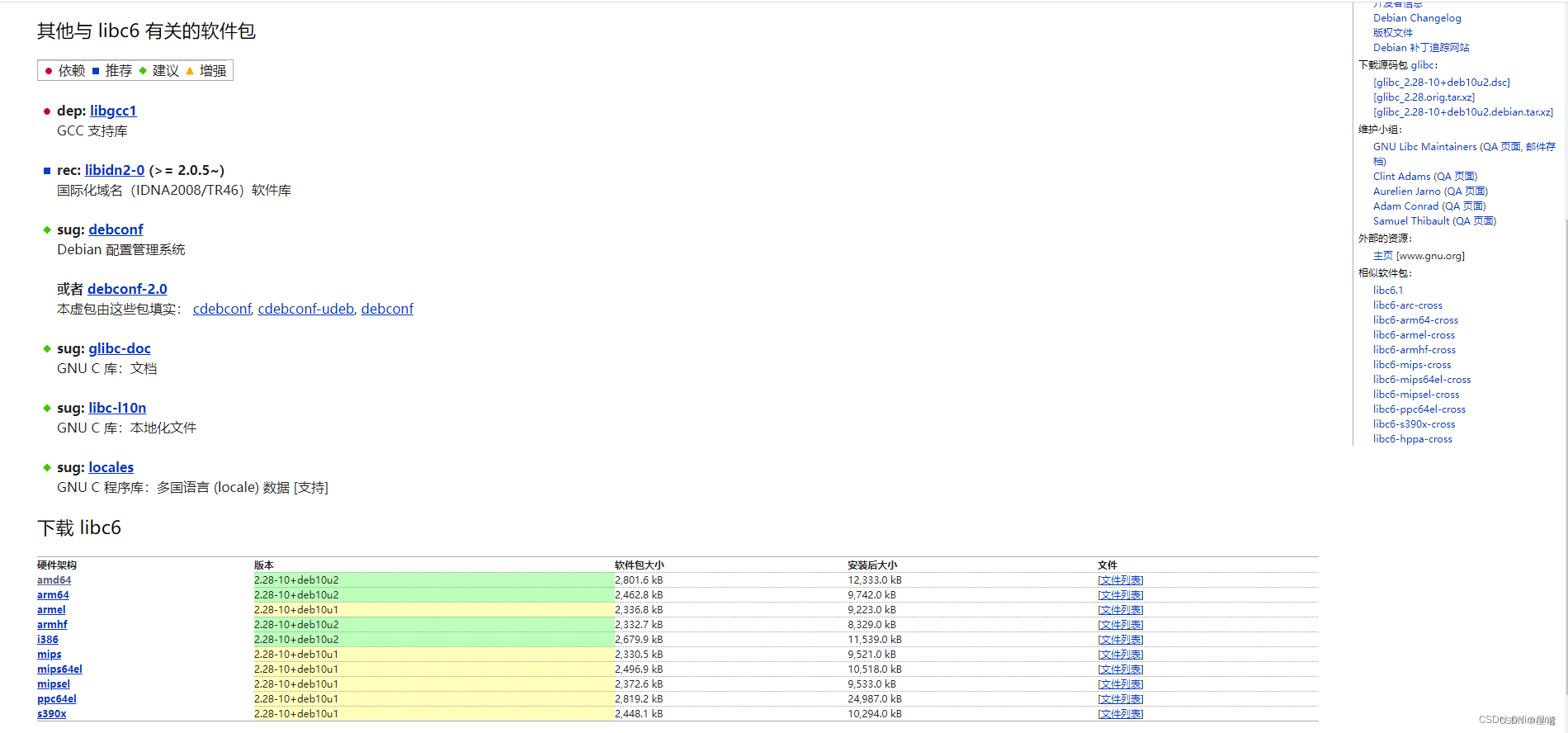
Ubuntu 18.04 出现GLIBC_2.28 not found的解决方法 参考debian网址https://packages.debian.org/buster/并搜索想要的软件或者工具等,如libc6,有结果如下: 具体就不介绍了,请浏览官网了解。 第一步:添加软件源,在/et…...
【Java EE初阶二十一】http的简单理解(二)
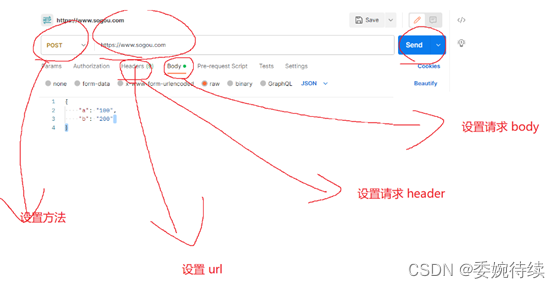
2. 深入学习http 2.5 关于referer Referer 描述了当前页面是从哪个页面跳转来的,如果是直接在地址栏输入 url(或者点击收藏夹中的按钮) 都是没有 Referer。如下图所示: HTTP 最大的问题在于"明文传输”,明文传输就容易被第三方获取并篡改. …...

STM32 与 ARM 谁比较强大?
STM32 和 ARM 是两个不同的概念,STM32 是一种微控制器产品,而 ARM 是一家处理器架构设计和许可的公司。因此,无法简单地比较它们的强大程度。 STM32 是基于 ARM Cortex-M 核的微控制器产品,具有高性能、低功耗、低成本和易于开发等…...

四、分类算法 - 朴素贝叶斯算法
目录 1、朴素贝叶斯算法 1.1 案例 1.2 联合概率、条件概率、相互独立 1.3 贝叶斯公式 1.4 朴素贝叶斯算法原理 1.5 应用场景 2、朴素贝叶斯算法对文本进行分类 2.1 案例 2.2 拉普拉斯平滑系数 3、API 4、案例:20类新闻分类 4.1 步骤分析 4.2 代码分析 …...
Javascript中var和let之间的区别
文章目录 一.变量提升(声)二.let和var的区别 区别: 1、var有变量提升,而let没有; 2、let不允许在相同的作用域下重复声明,而var允许; 3、let没有暂时性死区问题; 4、let创建的全局变量没有给window设置对应…...

不要抱怨,不如抱 Java 运算符吧 (1)
本篇会加入个人的所谓‘鱼式疯言’ ❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言 而是理解过并总结出来通俗易懂的大白话, 小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的. 🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人…...

python之ftp小工具
文章目录 python之FTP小工具 python之FTP小工具 源码 #!/usr/bin/python3 import os import sys from pyftpdlib.authorizers import DummyAuthorizer from pyftpdlib.handlers import FTPHandler, ThrottledDTPHandler from pyftpdlib.servers import FTPServer import logg…...
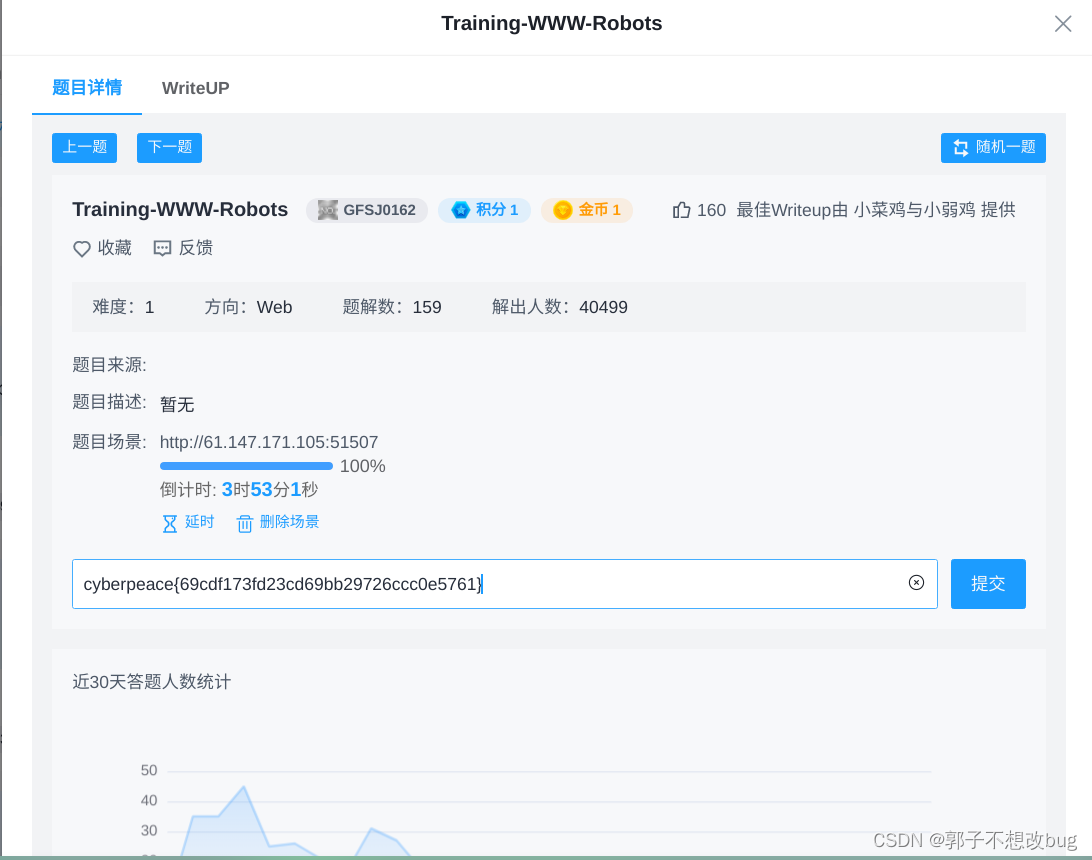
攻防世界-web-Training-WWW-Robots
题目信息 In this little training challenge, you are going to learn about the Robots_exclusion_standard. The robots.txt file is used by web crawlers to check if they are allowed to crawl and index your website or only parts of it. Sometimes these files rev…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
