算法--动态规划(背包问题)
这里写目录标题
- 总览
- dp问题的优化
- 01背包问题
- 概述
- 算法思想
- 算法思想中的注意点
- 例题+代码
- 完全背包问题
- 概述
- 多重背包问题
- 概述
- 分组背包问题
- 概述
总览

dp问题的优化

要清楚:dp问题的优化一般是对dp问题的代码或者计算方程做一个等效变形
有了这个前提,我们在写dp问题时,要先将基本的代码写出来,之后再做优化
01背包问题
概述

假设我们有N个物品,我们的背包的体积是V,
N个物品每个物品有两个属性,分别是v体积、和w价值,或者说权重,每个物品要么不选,如果选的话,只能选一次
我们的目标是:要选出一些物品,在总体积能装的下的情况下(不一定必须装满),争取价值之和最大化
算法思想

Dp问题,要考虑两个问题,一个是状态表示,一个是状态计算
对于01背包问题,
状态表示:
我们先来看状态表示,因为大前提是N个物品和V的体积,也就是不算物品属性的话,我们有两个参数,所以,状态表示f,就有两个参数,那他就是二维的状态表示,f(i,j)
而对于一个状态表示 f,我们要清楚,他是一个集合,那么一个集合就会有属性,一个集合有三种属性,根据不同的题设,选择不同的属性,三种属性分别是max(元素最大值)、min(元素最小值)、数量(元素数量),本题根据题设,是属性选定为max,表示求最大价值
那这个集合的元素表示什么呢,该集合的元素表示在所有的选法中,只从前 i 个物品选择,总体积小于等于 j 的选法
总结:状态表示就是将题意数学化,将题设信息数学化为 f(i,j)
状态计算:
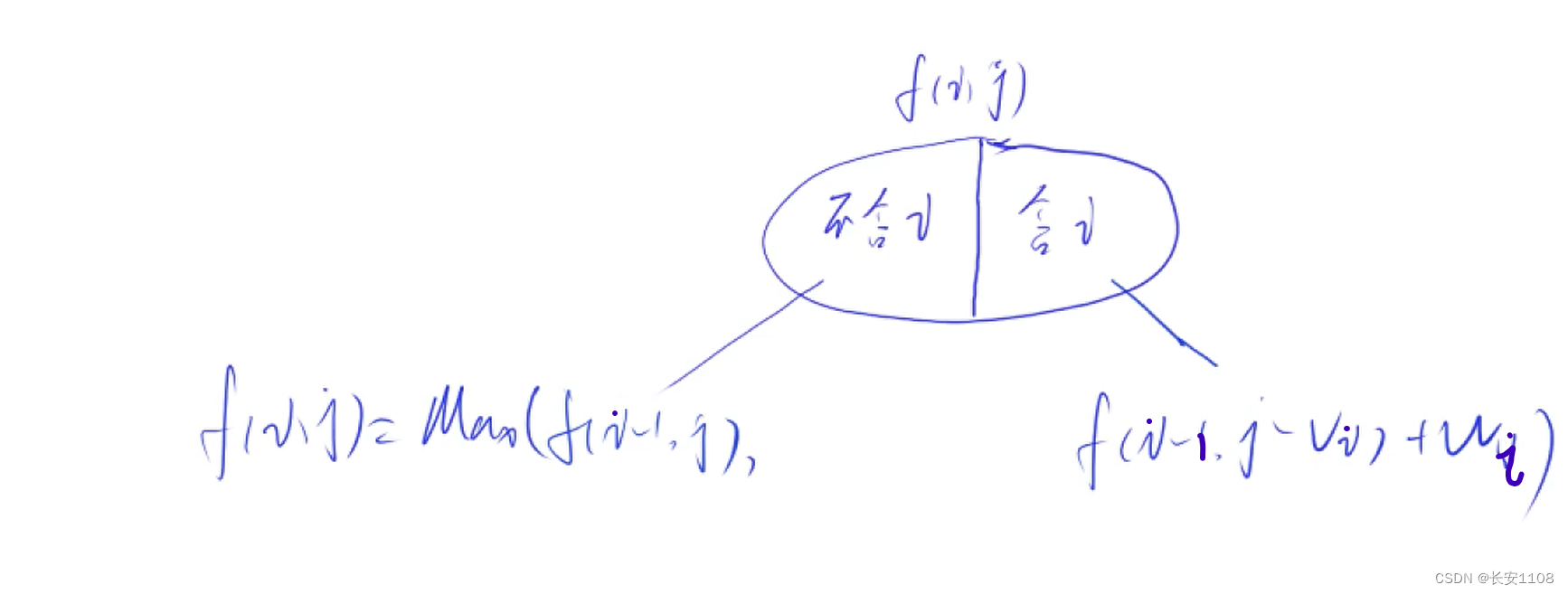
状态计算就是对上面的 f(i,j)进行计算,主要用到集合划分的思想
首先将集合划分为两部分,
第一个部分是 f 集合中所有不含 i 的选法的最大值,那么就是从1~i-1中选,总体积不超过 j ,也及时 f(i-1,j)
第二个部分是 f 集合中所有含 i 的选法的最大值,那么我们先将 i 排除,求得不算 i 时剩余的值最大的选法,因为排除了一个 i ,那么体积限制也跟着缩小,所以是从1~i-1中选,总体积不超过 j-vi 的选法的元素的最大值,即 f (i-1,j-vi)
最后,将两部分取maxAPI,求得 f(i,j),注意,因为第二部分是将 i 排除之后计算得出的,所以,在取max时,第二个参数要加上i的价值wi,即第二个参数为 f(i-1,j-vi)+ wi
如下三张图


算法思想中的注意点
首先,f(i,j)表示在前i个物品中选,总体积不超过 j 的选法,最大价值的值
这里的i 和 j 是通量,相当于将题设扩展成普遍性了,不是题设的最终量,也就是 i 和 j在代码中是变化的,最后是要输出f(N,V)
其次,对于状态计算,不含i的部分一定会出现,含i部分未必一定会出现,所以代码中要加一个判断,代码中会体现,注意留意
例题+代码


n,m分别表示有n个物品,总体积是m
v[N],w[N]数组,分别存储每个物品的体积和价值
f[N][N],是状态表示,也就是前i个物品中选,总体积不超过j的选法中,价值最大的值
main函数里,
首先输入n和m
然后for循环,依次向v,和w中输入值
之后,双重循环 i 从1到等于n,j从0到等于m(至于为什么i从1开始而不从0开始,是因为f[0][0~m],表示前0个物品中,选出体积不超过 j的选法,因为物品是0,所以总价值也是0,所以f[0][0到m]都是0,又因为int定义自动初始化为0,所以不用管 i =0的情况)
循环内,f[i][j] = f[i-1][j],先将这个赋值给f[i][j]
之后判断第二部分,因为第二部分只有在 j>=v[i]时,才会出现,所以加上if判断之后,f[i][j] = max( f[i][j] , f[i-1][ j-v[i] ] + w[i] )
(因为第一步直接将值赋给了f[i][j],所以这里是用f[i][j]进行对比,这样做的好处是,将第一部分与第二部分隔离开,因为第二部分需要特判)
完全背包问题
概述

完全背包问题,是每个物品有无限个,每个物品都可以选无限次
多重背包问题
概述

多重背包问题,是每个物品的个数不一样,也就是每个物品的可选次数不一样
分组背包问题
概述
分组背包问题,是会将物品进行分组,每一组最多只能选择改组内的一个物品,要么这个组不选,如果想选择这个组里的物品,只能选择改组内的一个物品且一次
相关文章:
算法--动态规划(背包问题)
这里写目录标题 总览dp问题的优化01背包问题概述算法思想算法思想中的注意点例题代码 完全背包问题概述 多重背包问题概述 分组背包问题概述 总览 dp问题的优化 要清楚:dp问题的优化一般是对dp问题的代码或者计算方程做一个等效变形 有了这个前提,我们在…...

Word 文档中的图片另存为 .jpg 格式图片
Word 文档中的图片另存为 .jpg 格式图片 1. Office 按钮 -> 另存为2. 筛选过的网页 (*.htm;*.html)3. 查看生成文件夹References 1. Office 按钮 -> 另存为 2. 筛选过的网页 (*.htm;*.html) 3. 查看生成文件夹 References [1] Yongqiang Cheng, https://yongq…...

【C++练级之路】【Lv.8】【STL】list类的模拟实现
快乐的流畅:个人主页 个人专栏:《C语言》《数据结构世界》《进击的C》 远方有一堆篝火,在为久候之人燃烧! 文章目录 引言一、结点二、迭代器2.1 成员变量与默认成员函数2.2 operator*2.3 operator->2.4 operator2.5 operator- …...

【右一的电子笔记】全导航,持续更新...
文章目录 📚计算机基础🐇高程(c)🐇python基础🐇数据结构🐇数据库系统概念🐇计算机网络🐇计算机组成原理🐇操作系统 📚大数据🐇大数据管…...

关于前端的console的方法的收集
console的常用方法列举 console.assert() 如果第一个参数为 false ,则将消息和堆栈跟踪记录到控制台。 console.clear() 清空控制台,并输出 Console was cleared。 console.count() 以参数为标识记录调用的次数,调用时在控制台打印标识…...
大工程 从0到1 数据治理 数仓篇(sample database classicmodels _No.7)
大工程 从0到1 数据治理 之数仓篇 我这里还是sample database classicmodels为案列,可以下载,我看 网上还没有类似的 案列,那就 从 0-1开始吧! 提示:写完文章后,目录可以自动生成,如何生成可参…...

phpcms v9敏感词内容替换
后台先在"扩展"——>"敏感词管理"中添加敏感词,然后修改phpcms\modules\content\content.php文件来实现添加或者编辑内容时敏感词的替换。(如果涉及会员投稿和留言等,也需要在对应模块中做类似处理) 在ad…...
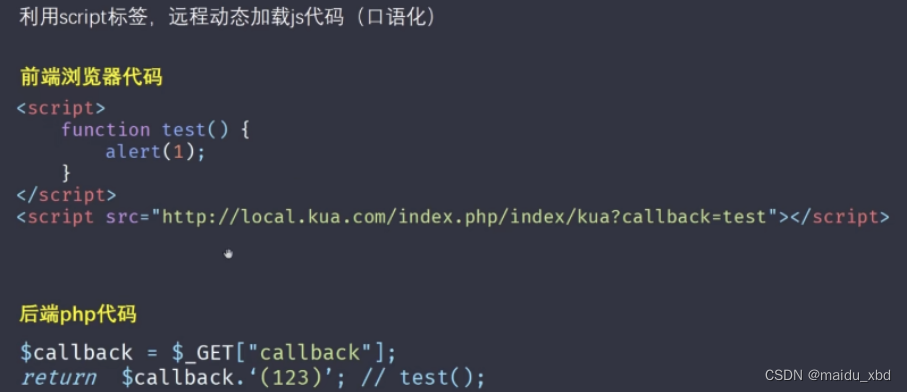
浏览器---浏览器/http相关面试题
1.localStorage和sessionStorage 共同点:二者都是以key-value的键值对方式存储在浏览器端,大小大概在5M。 区别: (1)数据有效期不同:sessionStorage仅在当前浏览器窗口关闭之前有效;localStorag…...

java 中开源的html解析库Jsoup 简单例子
下面是一个使用Jsoup库解析HTML的简单Java例子。这个例子展示了如何使用Jsoup从一个HTML字符串中提取数据。 首先,确保你已经将Jsoup作为依赖项添加到你的项目中。如果你使用的是Maven,可以在pom.xml文件中添加以下依赖: &…...

Java程序中为什么要使用StringBuilder
遇到这个问题是来源于leetcode的一道题:字符串解码。其中的题解涉及字符串的操作使用的是StringBuilder,不是String。 class Solution {public String decodeString(String s) {StringBuilder res new StringBuilder();int multi 0;LinkedList<Int…...
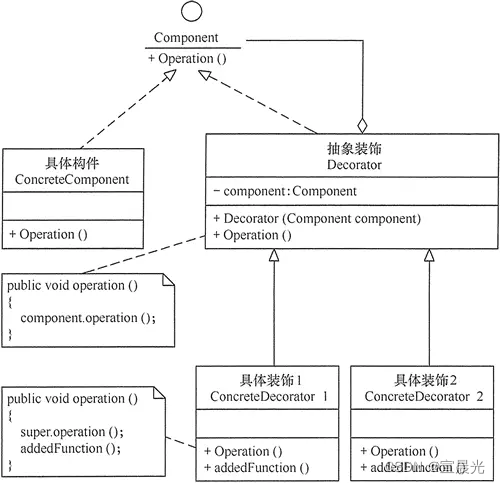
【软件架构】02-复杂度来源
1、性能 1)单机 受限于主机的CPU、网络、磁盘读写速度等影响 在多线程的互斥性、并发中的同步数据状态等; 扩展:硬件资源、增大线程池 2)集群 微服务化拆分,导致调用链过长,网络传输的消耗过多。 集…...
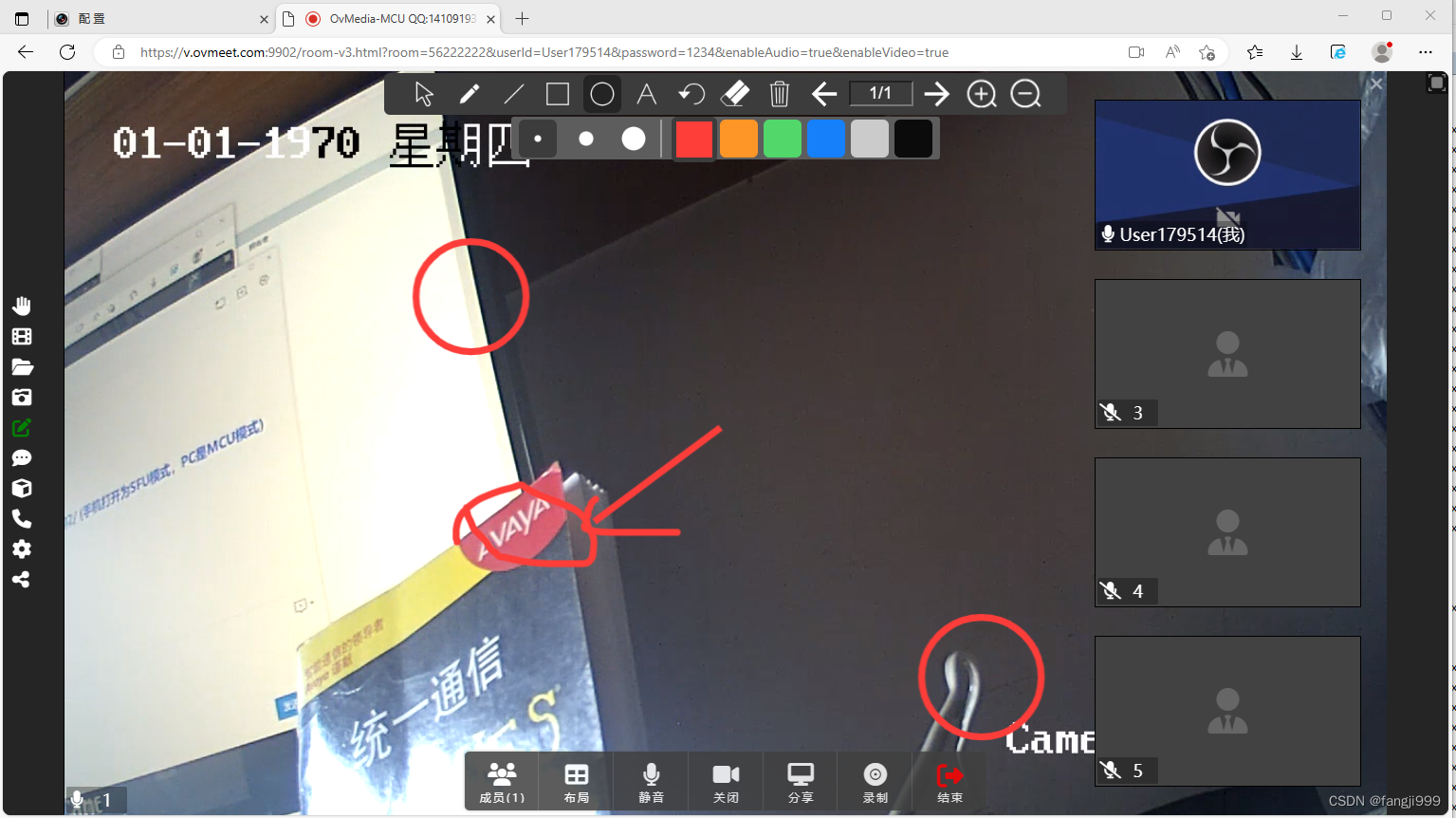
怎样让MCU/SFU视频会议ovmedia 接入GB28281监控视频参会互动
在国内视频应用对GB监控接入是常规操作,很多系统需要接入监控视频交互处理。我们以ovmedia视频会议为例做一个接入互动。 GB28181协议在流媒体系统较为普及,我们以开源SRS系统对接监控端再接入会议(也可以用商用GB流平台,操作基本…...
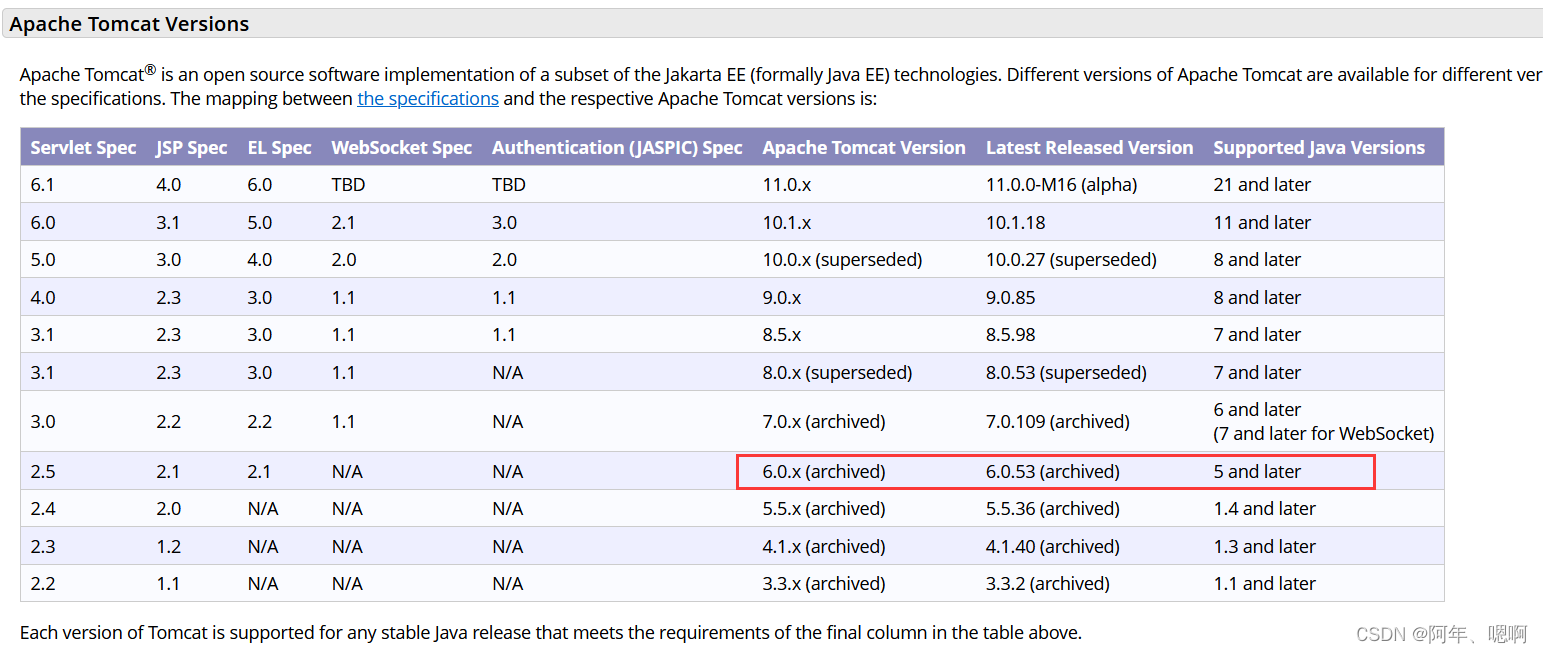
Spring Boot打war包部署到Tomcat,访问页面404 !!!
水善利万物而不争,处众人之所恶,故几于道💦 文章目录 Spring Boot打war包部署到Tomcat,访问页面404 !!!解决办法:检查Tomcat版本和Jdk的对应关系,我的Tomcat是6.x&#x…...
Docker Desktop 4.27.1 Windows 10 安装 教程
Docker Desktop 4.27.1 Windows 10 安装 版本要求windows 版本要求wsl 版本要求docker desktop 版本 安装首先确保系统版本符合要求前提下安装wsl安装 Dockers Desktop安装说明 安装问题docker Desktop 无法正常启动,提示wsl 相关信息wsl --install 执行输出帮助日志…...

【ARMv8M Cortex-M33 系列 8 -- RT-Thread 移植 posix pthread】
文章目录 RT-Thread POSIX PthreadRT-Thread Pthread 相关宏定义RT-Thread libc 初始化RT-Thread Pthread 测试 RT-Thread POSIX Pthread pthread是POSIX(Portable Operating System Interface)标准定义的一套线程相关的API,全称为POSIX Thr…...

fastApi笔记08-Cookie和Header
Cookie 可以像Query,Path,Body等同样的方式来定义Cookie参数 from typing import Annotatedfrom fastapi import Cookie, FastAPIapp FastAPI()app.get("/items/") async def read_items(ads_id: Annotated[str | None, Cookie()] None):r…...
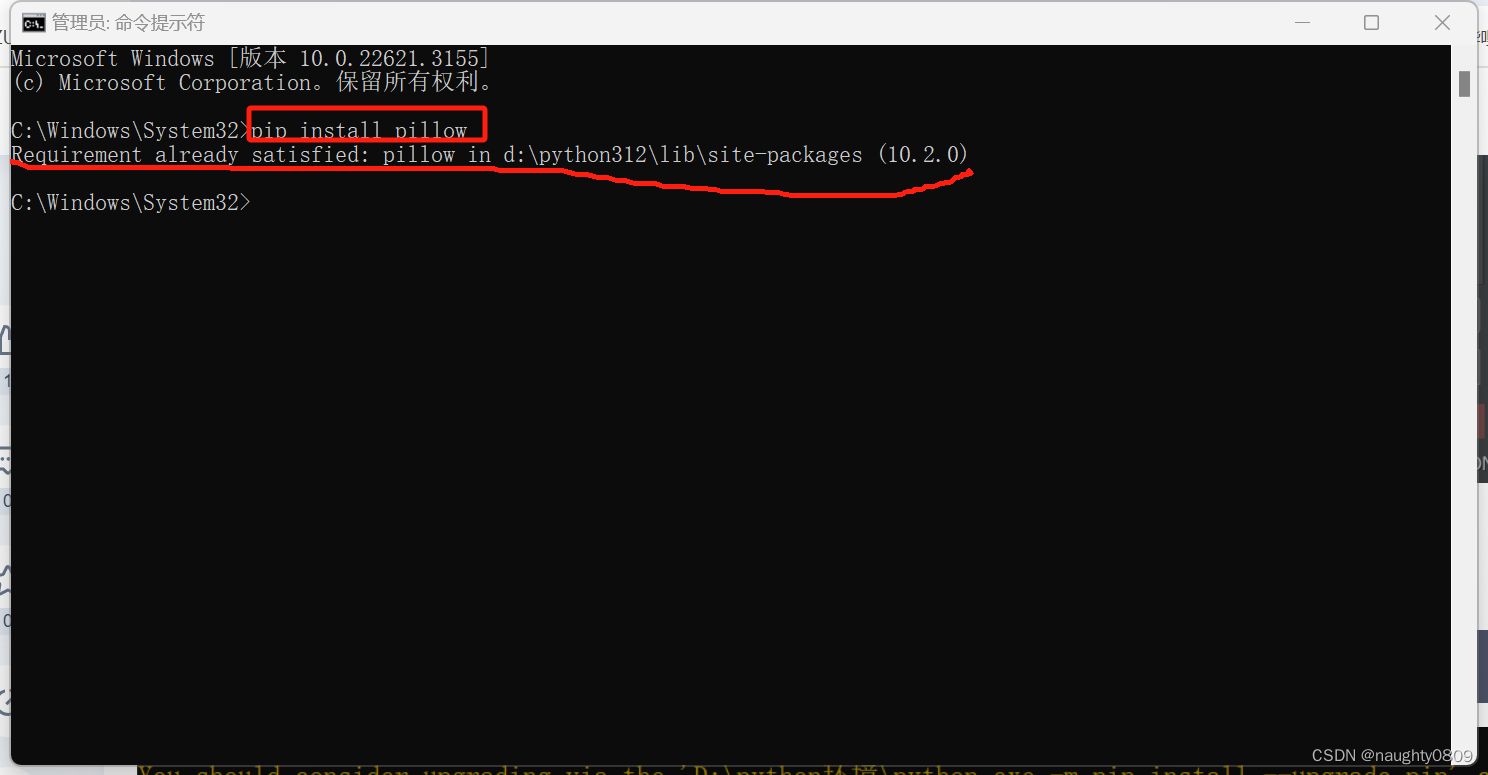
解决pycharm中PIL安装失败
问题:在调用pil时显示pil标红 我在设置中下载每次失败,显示 ERROR: Could not find a version that satisfies the requirement PIL (from versions: none) ERROR: No matching distribution found for PIL我尝试了很久,查看了一些博客 &a…...
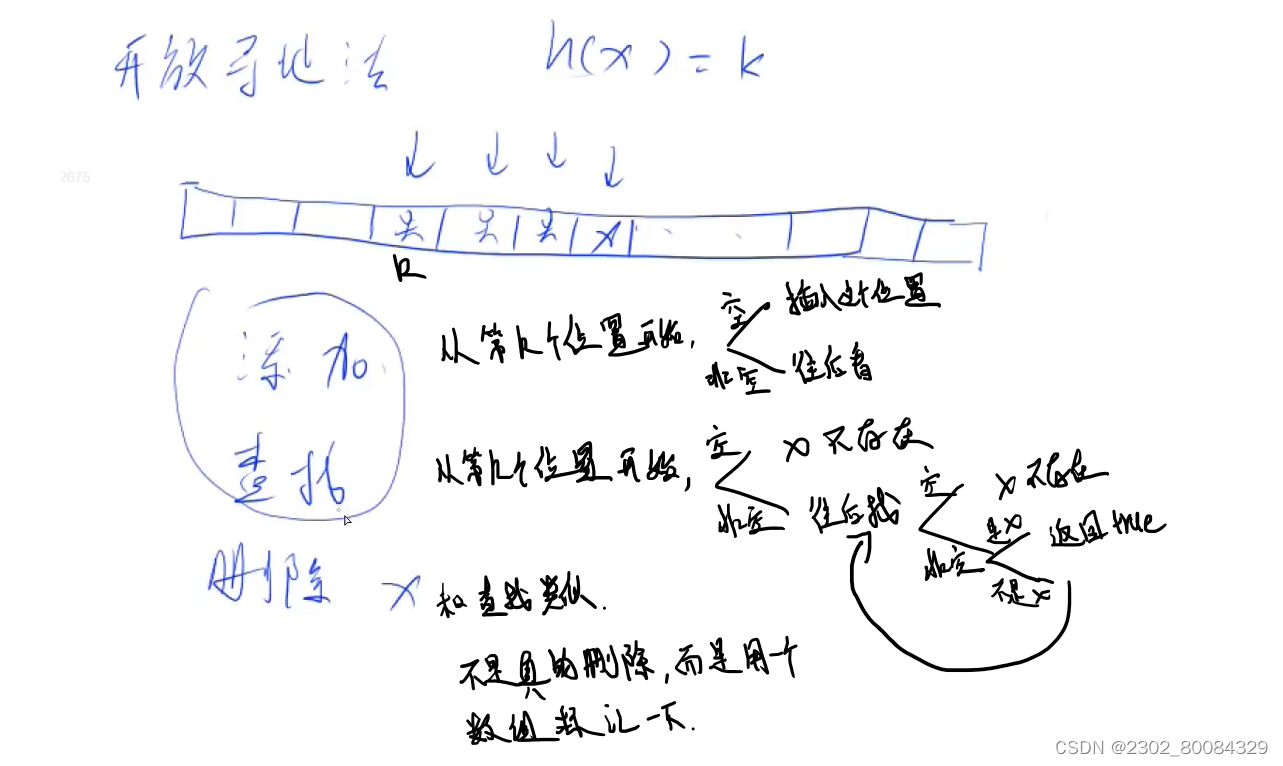
数据结构哈希表
这里个大家用数组来模拟哈希表 法一:拉链法 法二:开放寻址法 /** Project: 11_哈希表* File Created:Sunday, January 17th 2021, 2:11:23 pm* Author: Bug-Free* Problem:AcWing 840. 模拟散列表 拉链法*/ #include <cstring> #include <iostr…...
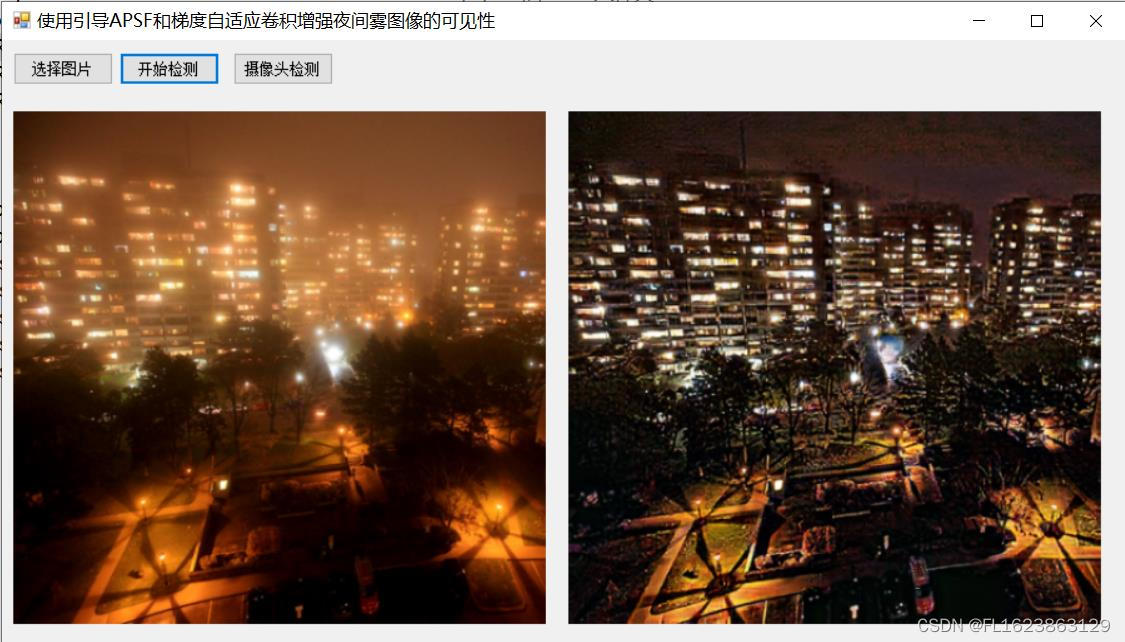
[C#]winform使用引导APSF和梯度自适应卷积增强夜间雾图像的可见性算法实现夜间雾霾图像的可见度增强
【算法介绍】 提升夜间雾霾图像可见度的技术研究:引导APSF与梯度自适应卷积的应用 随着城市化的快速发展,雾霾现象日益严重,尤其是在夜间,雾霾对图像的可见度造成了极大的影响。因此,提升夜间雾霾图像的可见度成为了…...
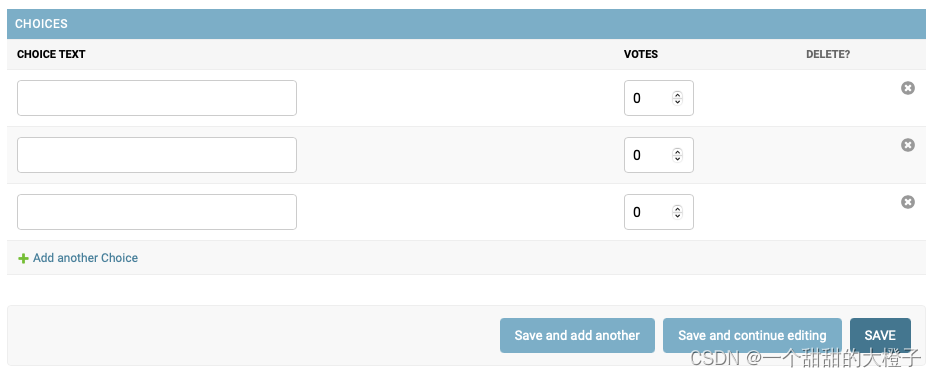
【Django】Django自定义后台表单——对一个关联外键对象同时添加多个内容
以官方文档为例: 一个投票问题包含多个选项,基本的表单设计只能一个选项一个选项添加,效率较低,如何在表单设计中一次性添加多个关联选项? 示例代码: from django.contrib import adminfrom .models impo…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
