排序算法整理
- 排序种类
- 排序特性
- 代码背景
- 基于插入的排序
- 直接插入排序
- 原理
- 代码
- 折半查找排序
- 2路查找排序
- 希尔排序(shell) 缩小增量排序
- 原理
- 代码
- 基于交换的排序
- 冒泡排序
- 原理
- 代码
- 快速排序(重要!)
- 原理
- 我的思考
- 代码
- 基于选择的排序
- (简单)选择排序
- 原理
- 代码
- 堆排序
- 原理
- 思考
- 代码
- 其他排序
- 归并排序(2路归并
- 原理
- 思考
- 代码
- 基于统计的排序
- 总结
本文是我学习排序算法的笔记,包含了知识点归纳、我对算法的思考、我的代码
如有误欢迎指出
本文使用语言:C++
排序种类
基于插入:直接插入排序算法、希尔排序算法
基于交换:冒泡排序算法、快速排序算法
基于选择:简单选择排序算法、堆排序算法
其他:归并排序、基于计数的排序
(基于计数的排序无代码
排序特性
- 是否就地排序
- 是内部排序还是外部排序(外部排序就是用到外存了,如果排序的数据能一次放到内存中,直接在内存排序,不涉及与外存交互,就是内部排序)
- 稳定排序还是不稳定排序(稳定排序就是,“==”的数据,相对位置不用变化
- 时间复杂度
文末有特性总结
代码背景
所有代码都用下方全局数组和main函数作测试
/*测试样例
20
23523 51345 1345314 9876 8765 2345 4 3 8 7
5 4 2349 1 54 29 53 98 275946382 305
*/
#include <iostream>
using namespace std;
int nums[105];
int n;
int main()
{//数组初始化cin >> n;for (int i = 1; i <= n; i++){cin >> nums[i];}//任何一个排序算法的函数调用一次//排序后展示for (int i = 1; i <= n; i++){cout << nums[i] << ' ';}cout << endl;
}
基于插入的排序
直接插入排序
特性:就地、稳定(看插入位置如何选择)、O( n 2 n^2 n2)
原理
以数组第一个元素为有序区,后面都算无序,每一次有序区长度增加1,将加入的元素顺序插入有序区中,完成排序
代码
void straightInsertSort()
{int new_insert; //新插入数的值int insert_index; //新插入数的应该插入的位置for (int i = 2; i <= n; i++) //i表示有序区长度{new_insert = nums[i]; //插入有序区的元素值insert_index = i; //避免完全不需要插入,导致insert_index = 0 !!!!!!!!!!for (int j = 1; j < i; j++){if(new_insert < nums[j]) //找到需要插入的位置{insert_index = j;break;}}for (int j = i; j > insert_index; j--)//从插入位置到有序区末尾,整体向右滑动{nums[j] = nums[j-1];}nums[insert_index] = new_insert;}
}
折半查找排序
查找需要插入位置时使用二分查找的方式,优化效果很一bamn,因为查找到之后的插入操作仍然是O(n)
特性:就地、稳定(看插入位置如何选择)、O( n 2 n^2 n2)
2路查找排序
优化插入操作的时间复杂度,用循环数组减少一半插入时间,这样会让排序变成非就地的,然而还是O(N),效果依旧一bamn
特性:就地、稳定(看插入位置如何选择)、O( n 2 n^2 n2)
希尔排序(shell) 缩小增量排序
会发现,数据量少且基本有序时,插入排序效率很高
特性:就地、不稳定(因为进行了跳跃的插入排序),时间复杂度(最坏时间复杂度O( n 2 n^2 n2))
原理
那么,将数组切分成多个小段,依次插入排序(这个时候每一段的数据量就很少),然后依次将每一段拼起来(拼起来的时候就是基本有序的情况)
Q:如何分段(分组)?
A:分d组,就以d为增量,先分n/2组,排序,减少到n/4组,直到1组(取n/2就是希尔增量)

会发现,希尔排序的作用就体现在数据量多时,要将小的值插入左边,可以很快地跳着插入,因为每一组很小,但其实在原数组上又很远!如果是直接插入排序的话要挪一整条数据,但是分组后只用挪一点点数据
Q:那我怎么对每一个跳着连接的组排序,比较方便?
A:以d为排序时插入的增量,每插入完一次可以直接++,给另一个组进行插入,就可以一个for循环,给每个组都排序了!
这时也会发现,其实分组、排序过程中的组数都没必要算了,只需要遍历增量就行
代码
void shellSort()
{int d = n/2;int new_ins; //新插入的值while(d>0){for (int i = 1+d; i <= n; i++){new_ins = nums[i];int j;for ( j = i-d ; j > 0 ; j-= d)//从右往左找插入的位置,刚好适合 基本有序 的情况下进行直接插入排序{if(nums[j] > new_ins)nums[j+d] = nums[j];//后移elsebreak;}nums[j+d] = new_ins; //插入}d/=2;//缩小增量}
}
基于交换的排序
冒泡排序
特性:就地、稳定、O( n 2 n^2 n2)
原理
每一次依次比较相邻元素,把最大的值往最后交换
代码
优化本次循环完全排序好的情况
#include <iostream>
using namespace std;
int nums[105];
int n;void bubbleSort()
{bool sorted = true;int tmp;for (int i = 1; i <= n; i++){sorted = true; //优化已经完全排好序的情况,那已经局部排序好的情况呢?for (int j = 1; j <= n - i; j++){if (nums[j] > nums[j + 1])//交换{tmp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tmp;sorted = false;}}if (sorted)break;}
}
优化局(尾)部已经排序好的情况,确定出已经有序部分和⽆序部分的边界
void bubbleSort()
{int unSortedCnt = n; //未排序的头部的长度,乱序区长度int tmpUnSortedCnt = n;int tmp;while (unSortedCnt > 1) //未排序长度为1时即完全排好序了{for (int j = 1; j < unSortedCnt; j++){if (nums[j] > nums[j + 1]) //交换{tmp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tmp;tmpUnSortedCnt = j; //更新,最后一次更新时就表示当前j到n都是有序的}}if (tmpUnSortedCnt == unSortedCnt)//没有更新,说明已经完全排好序break;unSortedCnt = tmpUnSortedCnt;}
}
快速排序(重要!)
特性:就地,不稳定,O(nlogn)
这里时间复杂度我的理解
- 每一层递归的时间复杂度O(n)
如果某时刻遍历到第 x x x 层,此时数组被拆成 2 x 2^x 2x 份,无论 2 x 2^x 2x 多大,这一层需要进行的比较(即类似下面代码中arr[i] > x的判断)都是n遍
即要走完数组内每一个元素(其实不完全准确,第 x x x 层的基准值到第 ( x + 1 ) (x+1) (x+1)层的时候就不需要进行比较了)
- 递归的趟数对应时间复杂度O(logn),原因参考下面我的思考
关于不稳定性:
数组中出现3个相等值,可能发生位置变化
原理
选一个基准 x x x 作“中点”,把小于 x x x 的放 x x x 左边,大于 x x x 的放右边,依次继续在左右进行这个操作(这个操作完成后基准 x x x 的位置就已经确定了,这个基准 x x x 就是“已排序”状态了)直到完成排序
实现:
以左边为基准,在尾部往头找比基准小的数,在头部往尾部找比基准大的数,依次交换
这个排序包含了递归的思想,所以这会是个递归函数
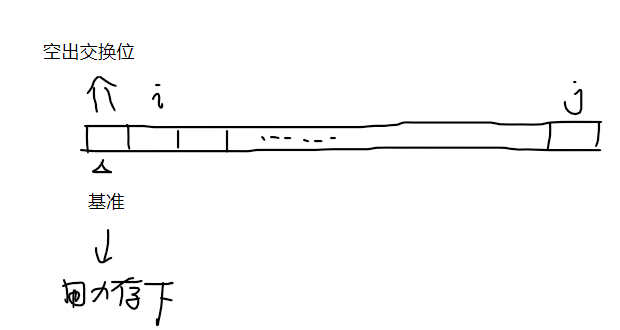
举例:
下面是定位一次基准值的步骤
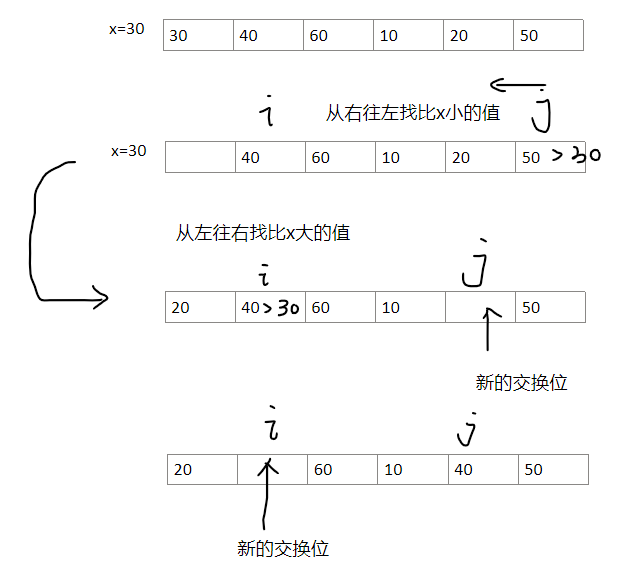
最终得到:
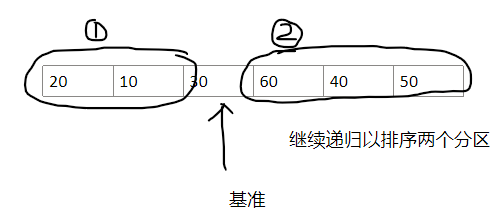
我的思考
快速排序思想里最核心的就是这个基准分界带来的倍增作用,因为每一次把一个基准值定位成功,都会让下一次时间复杂度为 O ( n ) O(n) O(n) 的一趟遍历定位基准值的数量翻倍(注意,但是如果这个基准值是当前区间的最值的话就不会翻倍
如上面的例子,第一遍遍历确认了 30 30 30 的位置,那么下一次遍历就会确认出 20 20 20 和 60 60 60 两个数!所以,遍历整个数组的趟数是 O ( l o g n ) O(logn) O(logn) 的,这是清清楚楚,一目了然的!
可以看出,快速排序的优秀之处,就是作为一个基于交换的排序(交换的时候会有位置互换,这个过程就能产生“信息”,比如基准值左边的值一定就在基准值左边,那么左边遍历完会有一个定位结果,右边就也一定会),在耗时为 O ( n ) O(n) O(n) 的定位操作的过程中(就是选择的过程),让下一次同样的一次遍历,通过交换定位出的基准位置得到的信息,得到更多的定位结果,以此提高效率
代码
/* 调用方式 quickSort(nums,1,n);
*/
void quickSort(int arr[],int l,int r)
{if(l<r){int i = l;int j = r;int x = arr[l];//为了避免每次交换需要用个tmp,我选择每次和x比较,最后再将x赋值到定位好的点while(i<j){while( i<j && arr[j] > x)j--;//从右往左找比x小的值if(i<j) arr[i++]=arr[j];//需要判断一下,避免已经j==i了,然后i++导致j<iwhile( i<j && arr[i] < x)i++;//从左往右找比x大的值if(i<j) arr[j--]=arr[i];}//最后还需要覆盖中间的基准值arr[i]=x;quickSort(arr,l,i-1);quickSort(arr,i+1,r);}
}
基于选择的排序
(简单)选择排序
特性:就地,不稳定,O( n 2 n^2 n2)
不稳定性来源于交换时,是跳跃的,比如{3,3,1},第一个3会跑到结尾
原理
每一次在待排序区中找最小的,放到最左边,依次直到待排序区长度为0
代码
void selectionSort()
{int min_p,tmp;for (int i = 1; i < n; i++){min_p=i;for (int j = i+1; j <= n; j++){if(nums[j]<nums[min_p]) min_p=j;}tmp = nums[i];nums[i] = nums[min_p];nums[min_p] = tmp;}
}
堆排序
特性:就地,不稳定,O(nlogn)
不稳定性:显然堆的调整的跳跃性会让重复数据相对位置发生改变
原理
堆可以实现用 O ( l o g n ) O(logn) O(logn) 的时间复杂度调整出最小值,来优化简单选择排序的效率
参考 大顶堆、小顶堆 这一篇,可知,用调整堆内子树的方式,依次找最小值,在第一次找到最小值用 O ( n l o g n ) O(nlogn) O(nlogn) 之后(也就是堆初始化),每一次找最小值只需要完成一次堆调整的操作 O ( l o g n ) O(logn) O(logn),执行剩下的 n − 1 n-1 n−1 次
原理:
先初始化出小顶堆,然后将顶列入已排序区,将堆数组尾部的数组提到顶部,进行 O ( l o g n ) O(logn) O(logn)的堆调整操作,以此往复,直到每个顶都依次进入排序区
实现:
我的思路是为了排序的就地性,这样操作,作大顶堆,把顶和数组尾部交换(也就是已排序区是从数组尾部往头部生长的),这个操作即完成了排序区的 fill in,还完成了堆的更新,下一步就可以直接开始堆调整操作了
图示:最终就是从右往左依次变小,就是升序了
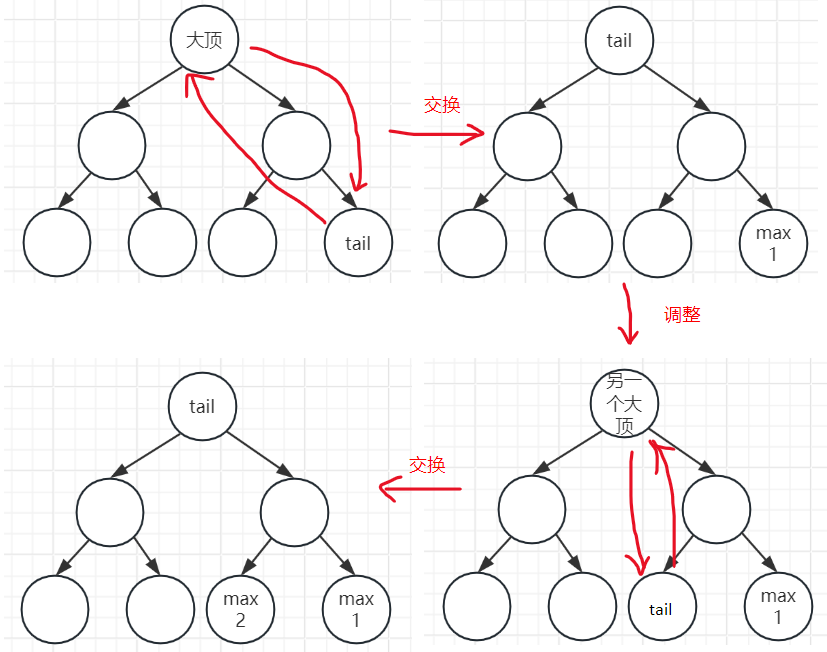
思考
这个思路的逻辑感觉和快速排序也是有相通之处的,快速排序让每次遍历排序的结果倍增,而堆排序让每次选择的效率翻倍
因为选择排序要做工作是,找到最值,压如排序区,往复
而找到最值的过程,也是有“信息”的,电脑记不住,但我们可以用一个逻辑帮他组织出来,堆排序用的就是堆的逻辑,
对一个大顶堆
我们 拿去根结点 = 找到最值,然后压入排序区,然后,我们替换根结点后,维护大顶堆,修复这个大顶堆 = 再次找到最值,而因为大顶堆的树状结构,我们找的新最大值已经在大顶堆根节点的左右手边上恭候多时了,只是为了保证下一次大顶堆每一个子树也是这个准备就绪的状态,需要 O ( l o g n ) O(logn) O(logn) 的维护时间,因为是树,每一次分支可以减少一半的判断,堆的维护也就比较高效
那为什么C++ sort()函数优先用快速排序而不是堆排序呢?
我没有做过调查研究,但是可以猜测一下,或许是在快速排序没有很坏的情况下,操作步数大致是 n l o g n nlog{n} nlogn,而堆排序因为数组自我初始化的过程就需要消耗大致 n 2 l o g n \frac{n}{2}logn 2nlogn 的步数了,完了排序还要操作 n l o g n nlogn nlogn 遍,可能会久一点,很无脑的猜测……
代码
/// @brief 维护大顶堆的函数(对子树A,A的子树都为大顶堆时,维护A子树的大顶堆状态
/// @param heap 堆数组
/// @param i 子树A根节点索引
/// @param n 子树A的最大索引值(尾部叶子
void adjustDown(int heap[],int i,int n)
{int child_p = 2 * i; //i结点(在循环中是指对应调整的子树)的孩子的索引int parent = heap[i]; //本子树的根结点的值while (child_p<=n) //保证双亲是有孩子结点的,叶子结点本身就是排好的堆,不需要调整{if (child_p + 1 <= n && heap[child_p + 1] > heap[child_p]) child_p++;//选中左右孩子中更小的和双亲作比较if (heap[child_p] > parent){heap[child_p / 2] = heap[child_p];//将孩子的值赋给父亲child_p *= 2;}else{break;}}heap[child_p/2] = parent;//这一步容易忘记!!!!就是赋回i结点的值!当然如果每次比较完用tmp去做交换就可以不用这么麻烦,我就是不想用tmp交换,因为那样有三次赋值,而这样写只有一次
}//堆排序代码
void heapSort()
{//初始化大顶堆for (int i = n/2; i > 0; i--){adjustDown(nums,i,n);}int tmp;for (int i = 1; i < n; i++)//在i=n-1并开始循环时,已排序区的长度为n-2,循环结束时已排序区长n-1,那头部也算是排好了,无需i=n再循环一遍{//头部和尾部交换(大顶堆的顶压如尾部已排序区tmp = nums[1];nums[1]=nums[n-i+1];nums[n-i+1]=tmp;//维护头部未排序区的大顶堆,此时只有根节点的树需要维护,其他的已经在初始化时维护好了adjustDown(nums,1,n-i);}
}
其他排序
归并排序(2路归并
特性:非就地,稳定,O(nlogn)
稳定性上,因为没有跳跃的比较交换,不会越过重复数据
原理
原理:
我倾向不以先拆再合并的方式去理解,他就是先以每一个单独的值作为已排好的数组,然后两两相邻的合并排序,最后合并成一个,显然就是合并 O ( n l o g n ) O(nlogn) O(nlogn) 趟
实现:
代码肯定还是从总数n出发,所以拆分2份,递归下去,直到长度为1,然后返回,得到的2份合并即可(本句搭配代码注释食用最佳
思考
先不说这个算法怎么做的,问一个问题,给你两个有序数组,把他俩放一起排序要多久, O ( n + m ) O(n+m) O(n+m) ,两个指针怼着两个数组的头然后遍历就行了,这就是归并排序的招式
所以就是线性复杂度的两两合并让已排序数组的长度翻倍,达到的高效,所以我认为功劳最大的是两已排序数组合并的线性时间复杂度,而不是这个二分合并(我也不知道咋叫,但学过二分查找的应该看得懂吧>_<)的思路,是这个线性时间复杂度给了归并排序用二分思想的底气
但是,但是,这个有序数组合并的过程,是需要开辟新的数组空间的,原因如下:
假设两数组为A、B(假设在原数组 n u m s nums nums中,A在左,B在右,AB相邻)
A [ i ] > B [ j ] A[i]>B[j] A[i]>B[j],并不能简单地将两者交换,因为 B [ j ] B[j] B[j]到 A A A里面是有序的,但是 A [ i ] A[i] A[i]到B里面就不一定了,为了提高时间效率,保证线性时间复杂度,需要开辟新的内存空间
代码
/* 调用方式mergeSort(nums,1,n);
*/
void mergeSort(int nums[],int l,int r)
{if(l>=r) return; //直到长度为1,然后返回int mid = l+(r-l)/2; //拆分2份mergeSort(nums,l,mid); //递归下去mergeSort(nums,mid+1,r); //得到的2份,合并即可int p1 = l;int p2 = mid+1;int tmpNums[105]; //临时数组与原数组等长int i = 1;while(p1<=mid && p2<=r){if(nums[p1]>nums[p2])tmpNums[i++]=nums[p2++];elsetmpNums[i++]=nums[p1++];}while(p1<=mid) tmpNums[i++]=nums[p1++];while(p2<=r) tmpNums[i++]=nums[p2++];i = 1;for (int j = l; j <= r; j++)//记得把临时表赋值回原表{nums[j] = tmpNums[i++];}
}
基于统计的排序
1. 计数排序
非就地,不稳定(可以优化为稳定的),时间复杂度O(n+b)(b是count数组的长度)但空间复杂度可能会很大,因为用于计数的数组长度可能过大,还可能导致时间复杂度大
原理:
- 记录最小、最大值,再记录从最小到最大值的所有数据的出现次数,存在count数组中
- count数组依次从小到大输出对应次数的值,完成排序
优化为稳定排序:
- 用一个index数组,作count的前缀和数组,意义是 i i i 这个值对应于排序好之后的最大索引
- 从原数组尾部遍历到头,遇到一个值,检索对应index数组的 “最大索引” ,这就是他应该呆的实际位置,然后对应index数组的 “最大索引” − 1 - 1 −1 即可
2. 桶排序
非就地,稳定性、时间复杂度取决于桶内排序效率
原理:
- 用数组内的值的范围分类,如每100一类,或每10一类(这样就可以通过 n u m s [ i ] / 10 nums[i]/10 nums[i]/10来分类),装在一个容器里
- 容器内再用之前的那些各种排序
- 最后合并
3. 基数排序
非就地,稳定,时间复杂度 O ( d × ( n + b ) ) O(d\times(n+b)) O(d×(n+b))(d是最大位数,b是count数组长度,10进制b=10
原理:(以十进制为例)
- 求出原数组的最高位(最低位
- 将所有数据补齐,填充0到最高位
- 从最低位开始,直到最高位,每一次对整个数组根据当前位数字进行稳定版本的计数排序即可
- 这样相当于用不同位进行有优先级的排序,优先级:高位的数字 > > > 低位的数字 > > > 原来处于数组的顺序
总结
| 算法 | 就地性 | 稳定性 | 时间复杂度 |
|---|---|---|---|
| 直接插入 | O | O | O( n 2 n^2 n2) |
| 希尔排序 | O | X | 最坏O( n 2 n^2 n2) |
| 冒泡排序 | O | O | O( n 2 n^2 n2) |
| 快速排序 | O | X | O( n l o g n nlogn nlogn) |
| 简单选择排序 | O | X | O( n 2 n^2 n2) |
| 堆排序 | O | X | O( n l o g n nlogn nlogn) |
| 归并排序 | X | O | O( n l o g n nlogn nlogn) |
| 计数排序 | X | X | O(n+b) |
| 桶排序 | X | 取决于桶内排序 | 取决于桶内排序 |
| 基数排序 | X | O | O ( d × ( n + b ) ) O(d\times(n+b)) O(d×(n+b)) |
相关文章:

排序算法整理
排序种类排序特性代码背景 基于插入的排序直接插入排序原理代码 折半查找排序2路查找排序希尔排序(shell) 缩小增量排序原理代码 基于交换的排序冒泡排序原理代码 快速排序(重要!)原理我的思考 代码 基于选择的排序(简单)选择排序…...

ONLYOFFICE 桌面应用程序 v8.0 发布:全新 RTL 界面、本地主题、Moodle 集成等你期待的功能来了!
目录 📘 前言 📟 一、什么是 ONLYOFFICE 桌面编辑器? 📟 二、ONLYOFFICE 8.0版本新增了那些特别的实用模块? 2.1. 可填写的 PDF 表单 2.2. 双向文本 2.3. 电子表格中的新增功能 单变量求解:…...
c语言---数组(超级详细)
数组 一.数组的概念二. 一维数组的创建和初始化2.1数组的创建2.2数组的初始化错误的初始化 2.3 数组的类型 三. 一维数组的使用3.1数组的下标3.2数组元素的打印3.2数组元素的输入 四. 一维数组在内存中的存储五. 二维数组的创建5.1二维数组的概念5.2如何创建二维数组 六.二维数…...

神经网络权重初始化
诸神缄默不语-个人CSDN博文目录 (如果只想看代码,请直接跳到“方法”一节,开头我介绍我的常用方法,后面介绍具体的各种方案) 神经网络通过多层神经元相互连接构成,而这些连接的强度就是通过权重ÿ…...

代码随想录训练营第三十九天|62.不同路径63. 不同路径 II
62.不同路径 1确定dp数组(dp table)以及下标的含义 从(0,0)出发到(i,j)有 dp[i][j]种路径 2确定递推公式 dp[i][j]dp[i-1][j]dp[i][j-1] 3dp数组如何初始化 for(int i0;i<m…...
学习大数据所需的java基础(5)
文章目录 集合框架Collection接口迭代器迭代器基本使用迭代器底层原理并发修改异常 数据结构栈队列数组链表 List接口底层源码分析 LinkList集合LinkedList底层成员解释说明LinkedList中get方法的源码分析LinkedList中add方法的源码分析 增强for增强for的介绍以及基本使用发2.使…...
Python 光速入门课程
首先说一下,为啥小编在即PHP和Golang之后,为啥又要整Python,那是因为小编最近又拿起了 " 阿里天池 " 的东西,所以小编又不得不捡起来大概五年前学习的Python,本篇文章主要讲的是最基础版本,所以比…...

解决vite打包出现 “default“ is not exported by “node_modules/...问题
项目场景: vue3tsvite项目打包 问题描述 // codemirror 编辑器的相关资源 import Codemirror from codemirror;error during build: RollupError: "default" is not exported by "node_modules/vue/dist/vue.runtime.esm-bundler.js", impor…...

c语言strtok的使用
strtok函数的作用为以指定字符分割字符串,含有两个参数,第一个函数为待分割的字符串或者空指针NULL,第二个参数为分割字符集。 对一个字符串首次使用strtok时第一个参数应该是待分割字符串,strtok以指定字符完成第一次分割后&…...
hash,以及数据结构——map容器
1.hash是什么? 定义:hash,一般翻译做散列、杂凑,或音译为哈希,是把任意长度的输入(又叫做预映射pre-image)通过散列算法变换成固定长度的输出, 该输出就是散列值。这种转换是一种压缩映射&…...

AIoT网关 人工智能物联网网关
AIoT(人工智能物联网)作为新一代技术的代表,正以前所未有的速度改变着我们的生活方式。在这个智能时代,AIoT网关的重要性日益凸显。它不仅是连接智能设备和应用的关键,同时也是实现智能化家居、智慧城市和工业自动化的必备技术。 一…...

基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的鸟类识别系统(Python+PySide6界面+训练代码)
摘要:本文详细阐述了一个利用深度学习进行鸟类识别的系统,该系统集成了最新的YOLOv8算法,并与YOLOv7、YOLOv6、YOLOv5等先前版本进行了性能比较。该系统能够在图像、视频、实时视频流和批量文件中精确地识别和分类鸟类。文中不仅深入讲解了YO…...

核密度分析
一.算法介绍 核密度估计(Kernel Density Estimation)是一种用于估计数据分布的非参数统计方法。它可以用于多种目的和应用,包括: 数据可视化:核密度估计可以用来绘制平滑的密度曲线或热力图,从而直观地表…...

先进语言模型带来的变革与潜力
用户可以通过询问或交互方式与GPT-4这样的先进语言模型互动,开启通往知识宝库的大门,即时访问人类历史积累的知识、经验与智慧。像GPT-4这样的先进语言模型,能够将人类历史上积累的海量知识和经验整合并加以利用。通过深度学习和大规模数据训…...
重铸安卓荣光——上传图片组件
痛点: 公司打算做安卓软件,最近在研究安卓,打算先绘制样式 研究发现安卓并不像前端有那么多组件库,甚至有些基础的组件都需要自己实现,记录一下自己实现的组件 成品展示 一个上传图片的组件 可以选择拍照或者从相册中…...
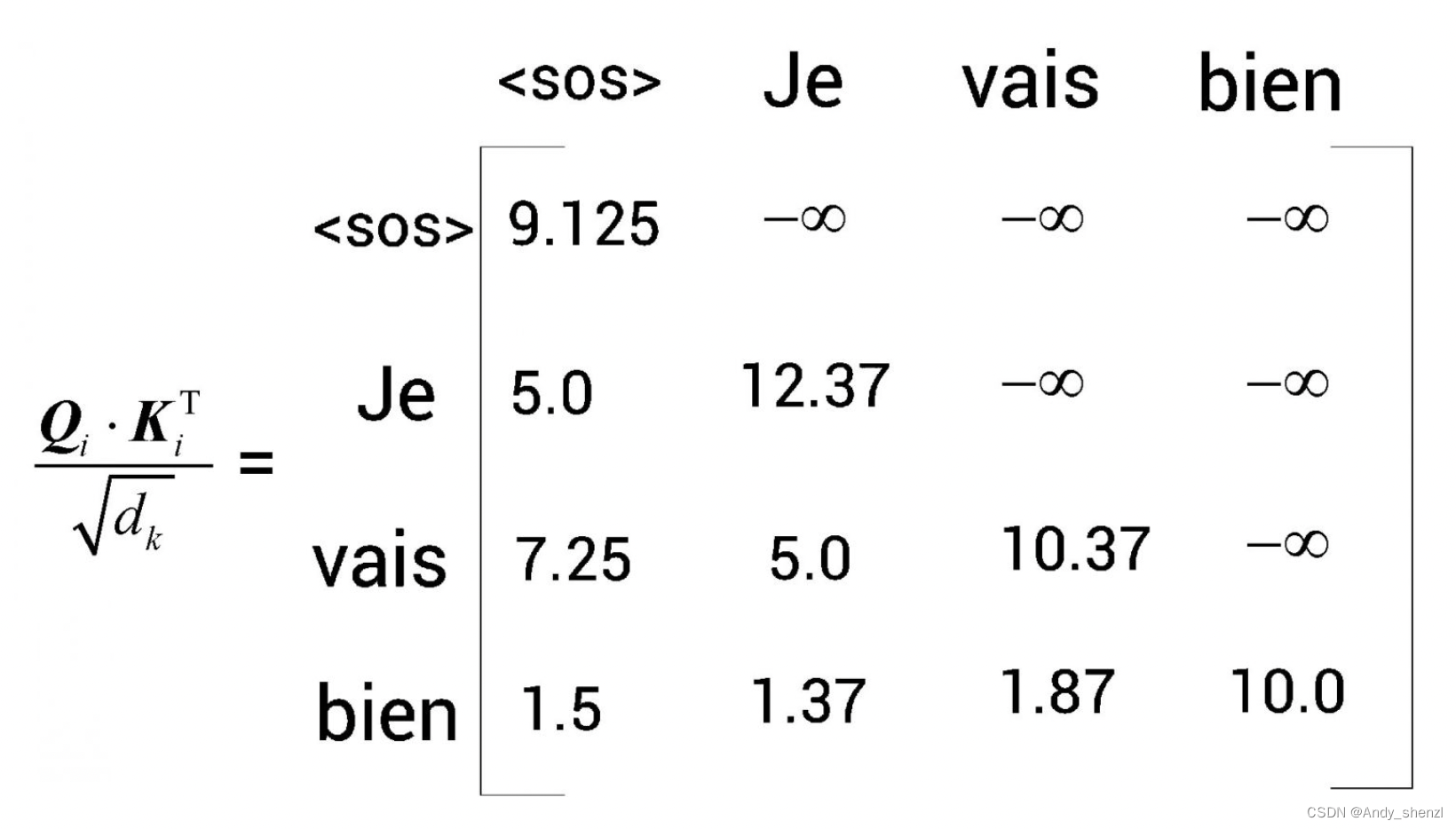
Bert基础(四)--解码器(上)
1 理解解码器 假设我们想把英语句子I am good(原句)翻译成法语句子Je vais bien(目标句)。首先,将原句I am good送入编码器,使编码器学习原句,并计算特征值。在前文中,我们学习了编…...

Visual Studio快捷键记录
日常使用Visual Studio进行开发,记录一下常用的快捷键: 复制:CtrlC剪切:CtrlX粘贴:CtrlV删除:CtrlL撤销:CtrlZ反撤销:CtrlY查找:CtrlF/CtrlI替换:CtrlH框式选…...

分享84个Html个人模板,总有一款适合您
分享84个Html个人模板,总有一款适合您 84个Html个人模板下载链接:https://pan.baidu.com/s/1GXUZlKPzmHvxtO0sm3gHLg?pwd8888 提取码:8888 Python采集代码下载链接:采集代码.zip - 蓝奏云 学习知识费力气,收集…...

vue使用.sync和update实现父组件与子组件数据绑定的案例
在 Vue 中,.sync 是一个用于实现双向数据绑定的特殊修饰符。它允许父组件通过一种简洁的方式向子组件传递一个 prop,并在子组件中修改这个 prop 的值,然后将修改后的值反馈回父组件,实现双向数据绑定。 使用 .sync 修饰符的基本语…...

C语言系列15——C语言的安全性与防御性编程
目录 写在开头1 缓冲区溢出:如何防范与处理1.1 缓冲区溢出的原因1.2 预防与处理策略 2. 安全的字符串处理函数与使用技巧2.1 strncpy函数2.2 snprintf函数2.3 strlcpy函数2.4 使用技巧 3 防御性编程的基本原则与实际方法3.1 基本原则3.2 实际方法 写在最后 写在开头…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...
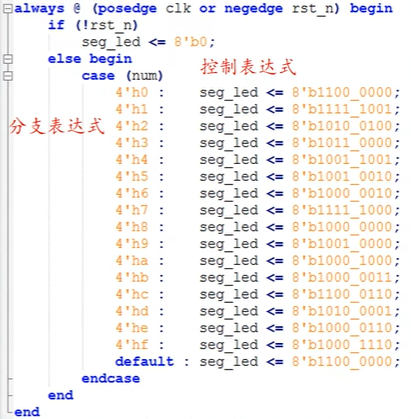
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...
